无隔水管海底泵举升系统循环温度变化动态模拟

张 杰 ，李 鑫，王志伟，李翠楠，杜肖潇

1.油气藏地质及开发工程国家重点实验室·西南石油大学，四川 成都 610500

2.中海石油（中国）有限公司深圳分公司，广东 深圳 518000

3.中国石油西南油气田分公司工程技术研究院，四川 广汉 618300

引言

无隔水管海底泵举升（Riserless Mud Recovery，RMR）系统是由挪威AGR 公司于2001 年所研发的一项针对深水窄安全密度窗口的双梯度钻井技术[1-5]，该系统主要构成如图1 所示。RMR 系统通过海床上所安装的吸入模块对环空返至海底井口的钻井液进行收集，并通过海底泵的举升作用将海底井口处的钻井液沿着小直径回流管线举升至钻井平台或钻井船[6-8]。另外，RMR 系统通过调整海底泵的排量使其作用于海底井口处的压力与作业水深下的海水静压力相等，保持海床以上为海水静压力梯度，海床以下为钻井液循环压力梯度，从而实现双梯度压力控制[9-11]。

图1 RMR 系统的主要构成示意图Fig.1 Main components of RMR system

由于RMR 系统不使用隔水管，在海水段的钻柱直接暴露于海水中，导致钻柱内的钻井液会与外部的海水进行换热。另外，该部分钻柱与用于钻井液上返的回流管线为两个相互独立的单元，二者之间不存在相互的热量交换过程，这使得RMR 系统在进行深水钻井作业时的流体循环温度变化特征与常规海洋钻井技术存在着很大的不同，而温度又是影响各项钻井作业参数的关键因素。因此，有必要结合RMR 系统的结构特点，针对系统内流体循环温度的变化特征开展相应的研究工作。

考虑到系统内流体流动的空间结构（海水段钻柱、地层段钻柱和环空、海水段回流管线）所处环境不同且海水段的结构又相互独立，为了便于对各结构内的流体循环温度变化进行模拟，首先，以各结构内流体的换热方式为依据，采用分段分析的方法，依次建立了用于不同结构内流体循环温度计算的动态分析模型。其次，通过将该模型的模拟结果与Lima等[12]和Pereira[13]解析解模型的模拟结果进行对比验证，保证模拟结果的准确性。最后，使用该模型对不同作业时长、钻井液密度和作业水深下的全系统循环温度变化进行了动态模拟，并对不同条件下的温度变化特征进行定性分析。该项研究成果有望为使用RMR 系统进行深水钻井作业时的全系统流体循环温度管理提供一定的理论依据。

1 物理模型

RMR 系统循环温度模拟动态分析模型的建立需以系统各结构内的流体换热方式为基础。由于RMR 系统各结构所处的自然环境以及相应结构内的流体换热方式都存在着不同，因此，在建立用于全系统循环温度变化模拟的数学模型之前，建立用于分析RMR 系统各结构内流体换热方式的物理模型具有十分重要的指导意义。RMR 系统相应结构内的流体换热物理模型如图2 所示。

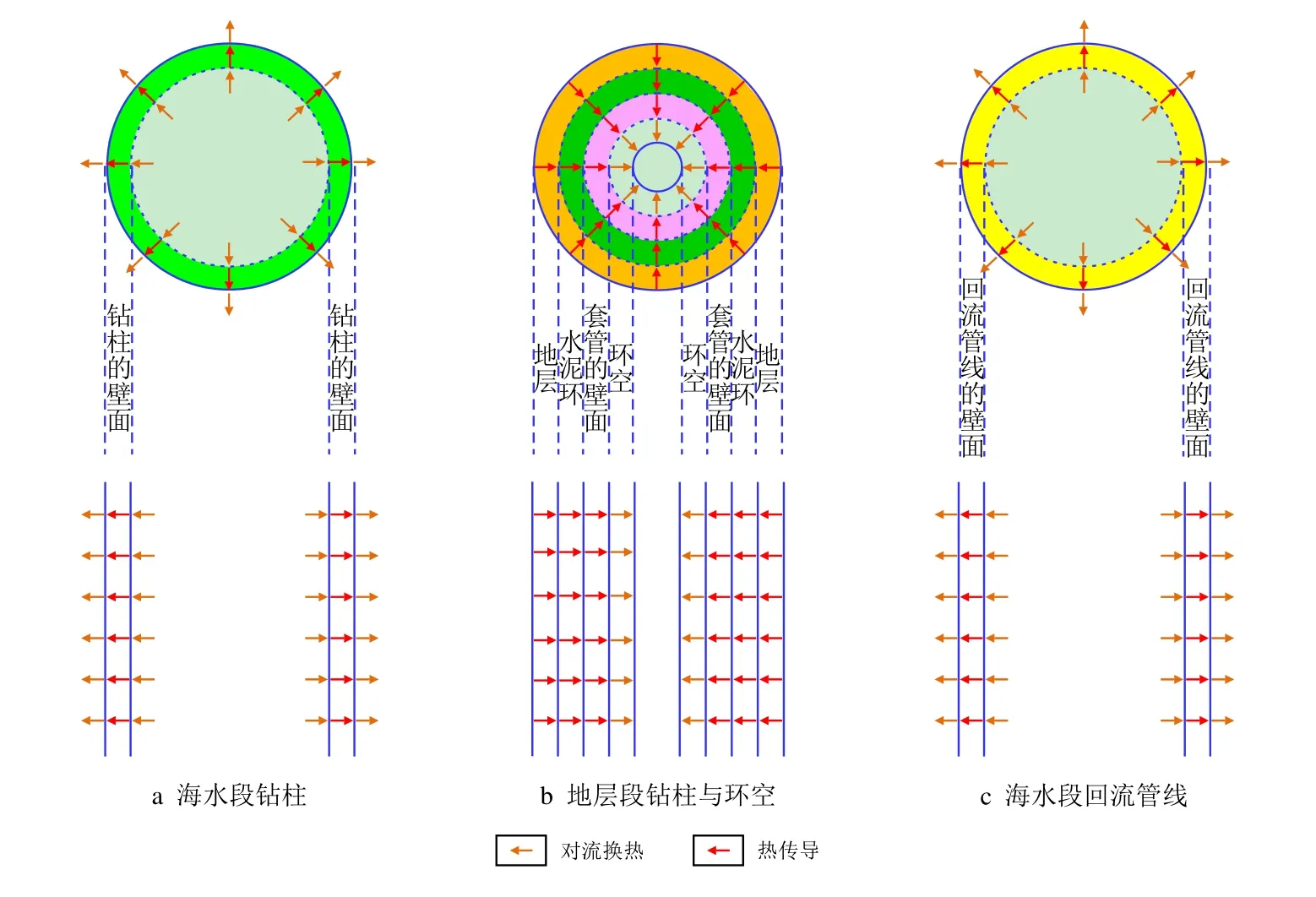
图2 RMR 系统各结构内流体换热的物理模型Fig.2 Physical model of fluid heat transfer in each component of RMR system

从图2 可见，由于海水段的钻柱直接暴露于海水中，且海水的温度往往较低，钻柱内的钻井液会通过对流换热与热传导相结合的复合换热方式将其热量通过钻柱内壁面和钻柱外壁面向外部的海水传递，这一点与常规海洋钻井技术的流体换热方式[14-17]存在着很大的不同，但地层段钻柱和环空内流体的换热方式仍与常规海洋钻井技术保持相同。另外，在深水环境下，海底处的海水温度往往仅有几度，从环空上返至海底井口的钻井液的温度会高于外部海水的温度[18-22]。因此，海水段回流管线内的钻井液也同样会通过对流换热和热传导相结合的复合换热方式将其热量向外部的海水传递。

2 数学模型

2.1 假设条件

本文所建立的动态分析模型主要基于以下假设条件：

（1）忽略钻井液的径向温度变化；

（2）忽略套管、钻柱和水泥环的热惯量；

（3）不考虑钻井过程中岩屑进入环空对流体传热的影响；

（4）岩石密度、比热和导热率为常数，且比热和导热率在垂向和水平方向上一致；

（5）距离井筒一定远处的地层温度不受传热过程的影响，始终保持原始地层温度不变。

2.2 控制方程

在建立用于循环温度变化模拟的数学模型时，首先，应选取各构成部分内的钻井液流动方向为正方向，并在相应结构内截取单位长度的控制体。其次，依据各构成部分内的钻井液换热方式，推导相应换热作用发生时的热量计算方程。最后，依据热力学第一定律，将同一构成部分内的热量计算方程进行联立，从而得到相应构成部分内的对流-扩散方程。

2.2.1 海水段钻柱内的对流-扩散方程

dt时间内钻柱内的钻井液通过强迫对流换热传递到钻柱内壁面上的热量为

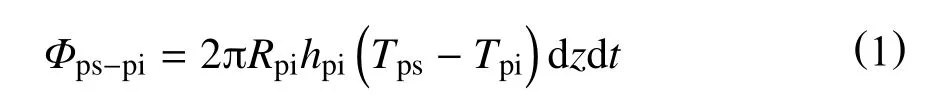
dt时间内，钻柱内壁面通过热传导传递到钻柱外壁面的热量为

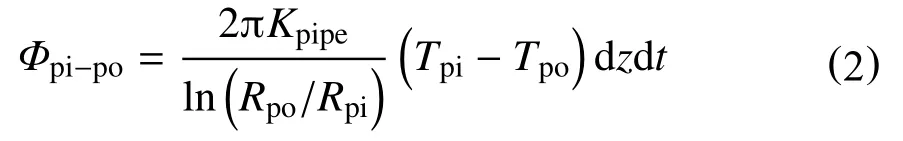
dt时间内，海水通过自然对流换热从钻柱外壁面吸收的热量为

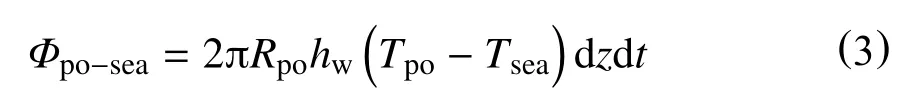
联立式（1）～式（3），可以得到在dt时间内海水段钻柱内的钻井液在径向上所传递的热量为

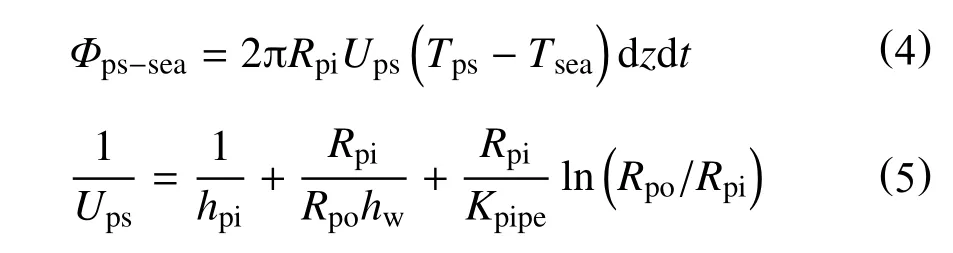
dt时间内，钻井液通过热传导从控制体上表面向其输入的热量为

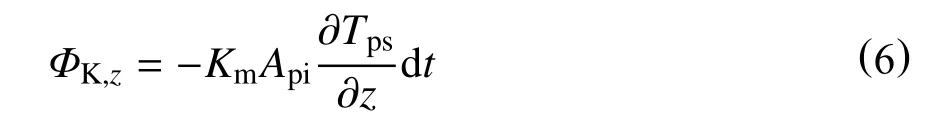
dt时间内，钻井液通过热传导从控制体下表面输出的热量为

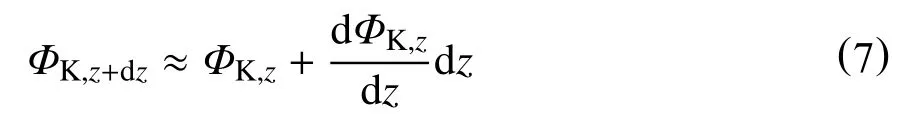
dt时间内，钻井液通过强迫对流换热从控制体上表面向其输入的热量为

dt时间内，钻井液通过强迫对流换热从控制体下表面输出的热量为

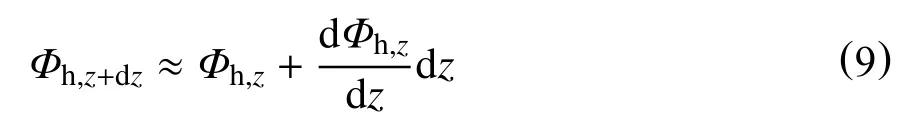
联立式（6）～式（9），可以得到，在dt时间内海水段钻柱内的钻井液在轴向上所传递的热量为

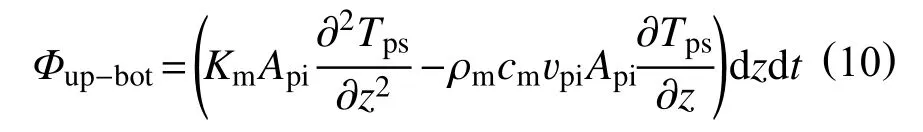
dt时间内，控制体内钻井液的内能增加量为

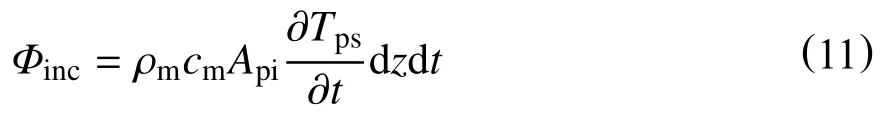
依据热力学第一定律，可以得到用于海水段钻柱内循环温度计算的对流-扩散方程为

2.2.2 地层段钻柱内的对流-扩散方程

dt时间内，环空内的钻井液通过强迫对流换热传递到钻柱外壁面上的热量为

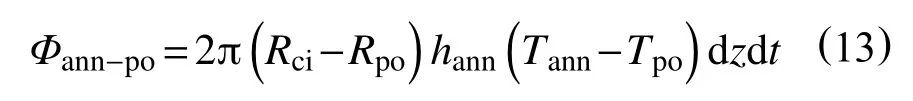
dt时间内，钻柱外壁面通过热传导传递到钻柱内壁面的热量为

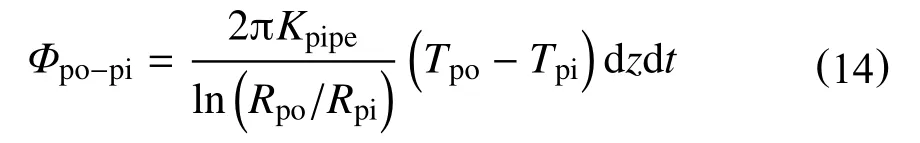
dt时间内，钻柱内钻井液通过强迫对流换热从钻柱内壁面携带走的热量为

联立式（13）～式（15），可以得到，在dt时间内地层段钻柱内的钻井液在径向上所传递的热量为

依据热力学第一定律，并结合钻柱内的钻井液在轴向上的热量计算方程，以及dt时间内控制体内钻井液内能增加量的计算方程，可以得到用于地层段钻柱内循环温度计算的对流-扩散方程为

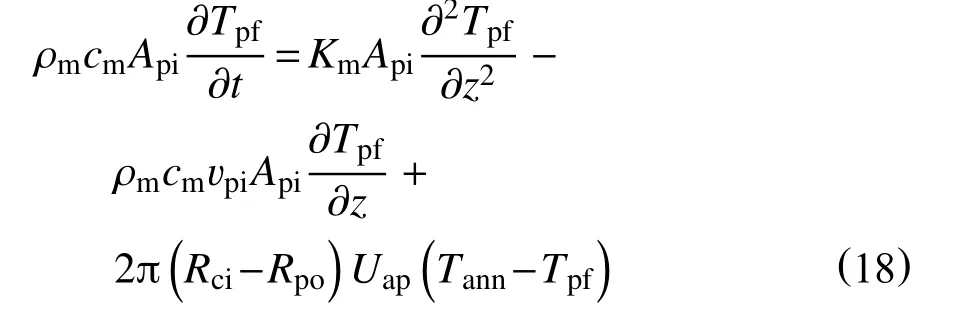
2.2.3 地层段环空内的对流-扩散方程

dt时间内，地层通过热传导传递到水泥环外壁面上的热量为

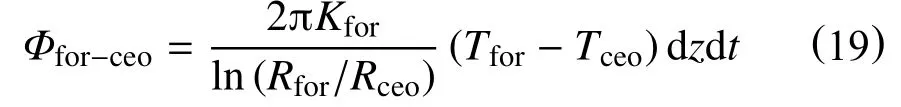
dt时间内，水泥环外壁面通过热传导传递到水泥环内壁面上的热量为

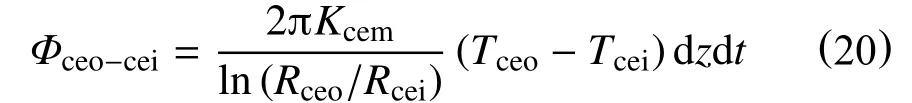
dt时间内，水泥环内壁面通过热传导传递到套管外壁面上的热量为

dt时间内，套管外壁面通过热传导传递到套管内壁面上的热量为

dt时间内，环空内钻井液通过强迫对流换热作用从套管内壁面吸收热量为

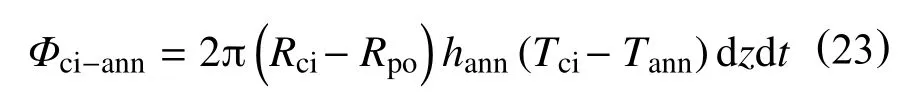
联立式（19）～式（23），可以得到在dt时间内地层向环空内钻井液所传递的热量为

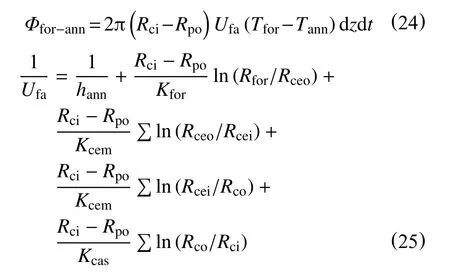
由热力学第一定律，结合式（16）和环空内的钻井液在轴向上的热量计算方程，以及dt时间内控制体内钻井液内能增加量的计算方程，可以得到用于地层段环空内循环温度计算的对流-扩散方程。

dt时间内，地层段环空内循环温度计算的对流-扩散方程为

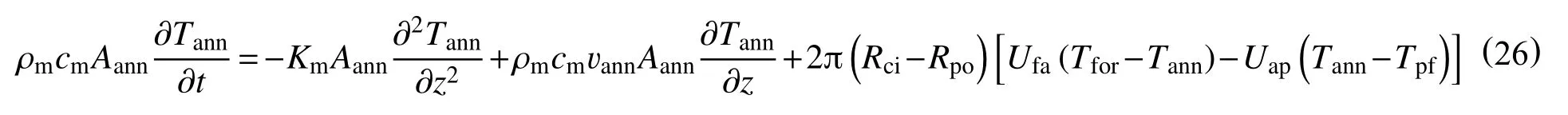
2.2.4 海水段回流管线内的对流-扩散方程

dt时间内，回流管线内的钻井液通过强迫对流换热传递到回流管线内壁面上的热量为

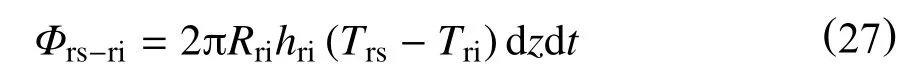
dt时间内，回流管线内壁面通过热传导传递到回流管线外壁面的热量为

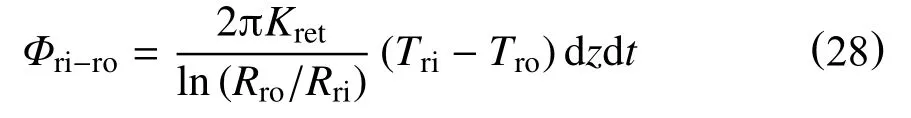
dt时间内，海水通过自然对流换热从回流管线外壁面吸收的热量为

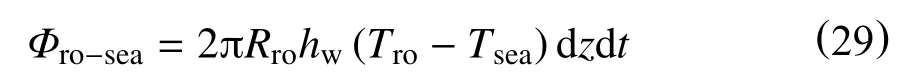
联立式（27）～式（29），可以得到在dt时间内海水段钻柱内的钻井液在径向上所传递的热量为

依据热力学第一定律，并结合回流管线内的钻井液在轴向上的热量计算方程，以及dt时间内控制体内钻井液的内能增加量的计算方程，可以得到回流管线内的对流-扩散方程为

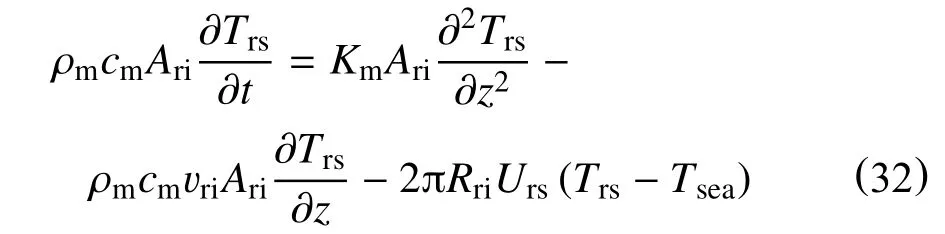
2.3 初始及边界条件

使用上述控制方程进行计算时，所使用的初始及边界条件如下：

（1）初始时刻，海水段钻柱和回流管线内的钻井液温度与外部海水温度相等，Tps=Trs=Tsea；

（2）初始时刻，地层段钻柱和环空内的钻井液温度与地层温度相等，Tpf=Tann=Tfor；

（3）在钻柱顶端节点处，钻井液的温度始终为注入温度，Tps=Tinjec；

（4）在井底节点处，地层段钻柱和环空内的钻井液温度相等，Tpf=Tann。

2.4 模型求解

2.4.1 空间离散化处理

由于RMR 系统各构成部分的结构都较为均匀，为了便于编写相应的计算程序且不对计算结果的准确性造成影响，采用内节点法对RMR 系统各构成部分的空间区域进行离散化处理，空间步长Δh设置为1 m。

2.4.2 方程离散化处理

将RMR 系统不同构成部分的对流-扩散方程在相应的节点上进行离散。时间项采用两点向前差分格式，一阶空间项采用两点向后差分格式，二阶空间项采用两点中心差分格式。将时间步长Δt设置为1 s。

3 模型验证

采用模型对比分析的方式来验证模拟结果的准确性，具体的井身结构数据如表1 所示，计算所用的热力参数如表2 所示。

表1 井身结构数据表Tab.1 Well structure data sheet

表2 计算所用热力参数表Tab.2 Thermal parameter table for calculation

验证时，设定从井深3 813 m 开始钻进，共用时12 h 钻至井深3 981 m。所使用的作业参数为：钻井液初始密度1.36 g/cm3，钻井液注入温度30°C，平均机械钻速14 m/h，钻井泵排量45 L/s，海底泵排量30 L/s，回流管线内径53.4 mm。环境参数为：作业水深1 200 m，海水表面温度25°C，地温梯度0.03°C/m。海水温度主要采用中国南海水温的计算方式[23-25]。

在钻井作业的过程中，分别使用动态分析模型、Lima 模型和Pereira 模型对全系统的循环温度变化进行模拟。

当钻进至3 981 m 时，3 种数学模型的模拟结果如图3 所示。

从图3 中可以看到，论文所建立的动态分析模型的模拟结果基本处于两种解析解模型之间。因此，模型的模拟结果具备较高的准确性。另外，相比于Lima 和Pereira 解析解模型，论文所建立的动态分析模型多考虑了时间因素的影响，可对不同作业时长下的循环温度变化进行动态模拟，这更加贴合钻井作业的实际情况。

图3 不同数学模型的模拟结果对比Fig.3 Comparison of simulation results for different mathematical models

4 结果分析与讨论

4.1 不同作业时长下的循环温度

在从3 813 m 钻至3 981 m 的过程中，钻井液会在系统内不断地循环。为了对不同作业时长下的温度剖面进行观察，论文通过使用所建立的动态分析模型，依次对作业2，4，6，8，10 和12 h 后的全系统循环温度变化进行了模拟，相应的模拟结果如图4 所示。从图4 可以看到，随着作业时长的增加，RMR 系统各构成部分内的循环温度会逐渐升高。

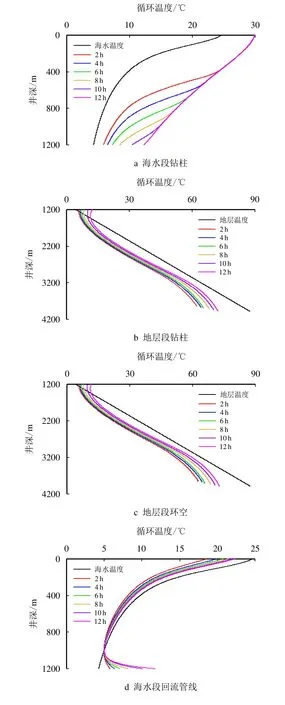
图4 不同作业时长下的循环温度变化模拟结果Fig.4 Simulation results of circulating temperature changes under different operating hours

发生这种变化的主要原因如下：

（1）随着作业时长的增加，注入的钻井液等同于一股热流体不断地从钻井平台向钻柱内注入，从而造成海水段钻柱内的循环温度逐渐升高。

（2）随着作业时长的增加，钻遇地层的温度逐渐升高，地层不断地向环空内钻井液传递热量，且环空内的钻井液也会不断地向钻柱内的钻井液传递热量，地层段相应部分内的循环温度逐渐升高。

（3）随着作业时长的增加，环空向回流管线内注入的钻井液温度升高，且当钻井液的温度低于海水温度时，海水也会不断地向回流管线内的钻井液传递热量，从而造成该部分的循环温度逐渐升高。

4.2 不同钻井液密度下的循环温度

钻井作业所使用的钻井液密度分别为1.36，1.56，1.76，1.96，2.16 和2.36 g/cm3，使用不同密度的钻井液钻至3 981 m 时的温度模拟结果如图5所示。

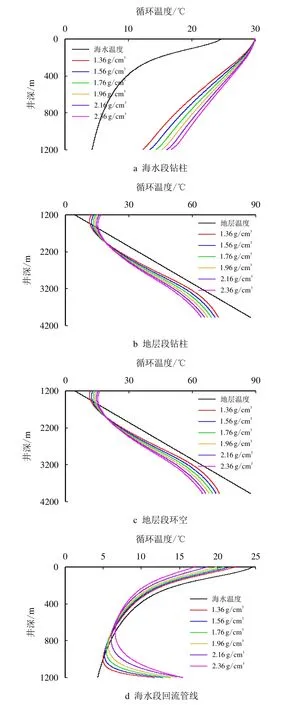
图5 不同钻井液密度下的循环温度变化模拟结果Fig.5 Simulation results of circulating temperature changes under different drilling fluid densities

由图5 可见，所使用的钻井液密度越大，海水段钻柱内的循环温度越高，地层段钻柱、环空和海水段回流管线内的循环温度越低。发生这种变化的主要原因是：钻井液的密度越大，其在系统内流动时的单位质量流量越大，故在吸收或释放相同的热量时，温度上升或下降的幅度越小。

4.3 不同作业水深下的循环温度

设定钻井作业过程中所处的作业水深分别为1 200，1 000，800，600，400 和200 m，在不同作业水深环境下钻至3 981 m 时的温度模拟结果如图6所示。由图6 可见，若钻井作业所处的作业水深越浅，则海水段钻柱内的循环温度越高，地层段下半部分钻柱和环空内的循环温度基本保持稳定，海水段回流管线内的循环温度越高。发生这种变化的主要原因是：（1）作业水深越浅，海水段钻柱内流体与外部海水进行换热的路径越短，向海水中传递的热量越少，故循环温度越高；（2）作业水深越浅，注入到地层段构成部分内的流体温度越高，导致地层向环空内流体传递的热量减少，环空向钻柱内流体传递的热量也同样减少，故地层段下半部分的循环温度基本保持稳定；（3）作业水深越浅，回流管线内流体开始从海水中吸收热量时的起始温度越高，故相应水深下的循环温度越高。

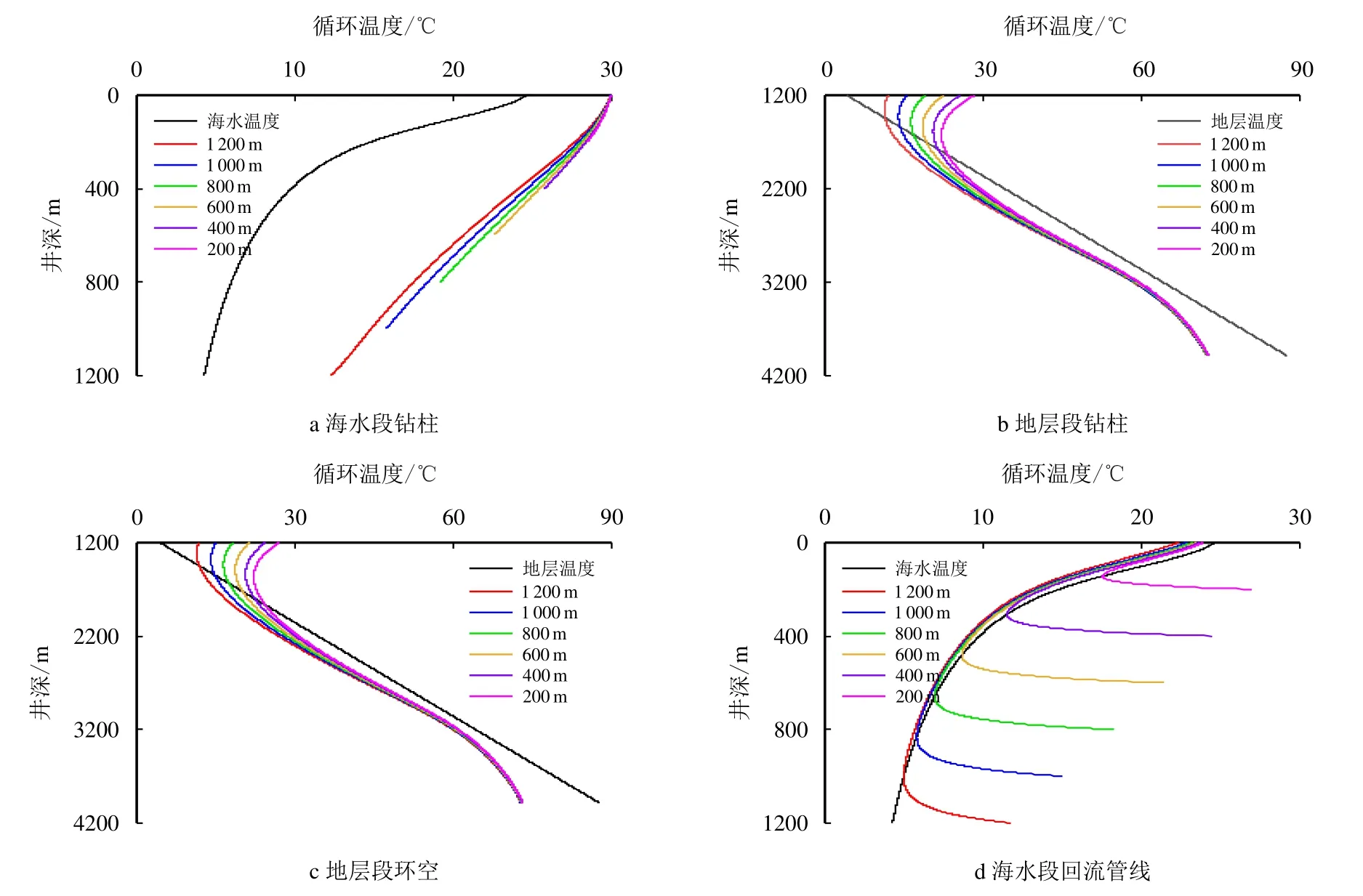
图6 不同作业水深下的循环温度变化模拟结果Fig.6 Simulation results of circulating temperature changes with different operating water depths

5 结论

（1）与Lima 和Pereira 解析解模型相比，论文所建立的动态分析模型进一步考虑了时间因素的影响，与实际的钻井作业情况更加贴合，且模拟的结果处于两种解析解模型之间，能够说明模型模拟结果的准确性。

（2）模拟结果表明，在模拟的作业时长从2 h 增加至12 h 的过程中，RMR 系统各构成部分内的流体循环温度均会随着作业时长的增加而逐渐升高。

（3）使用RMR 系统进行钻井作业时所使用的钻井液密度越高，RMR 系统海水段钻柱内的流体循环温度就会越高，但地层段钻柱、环空和海水段回流管线内的流体循环温度越低。

（4）使用RMR 系统进行钻井作业时所处的作业水深越浅，RMR 系统海水段钻柱及回流管线内的循环温度越高，但地层段下半部分钻柱和环空内的循环温度基本保持稳定。

符号说明