基于机构运动学的机器人标定方法

黄雨晨

(景德镇陶瓷大学机械电子工程学院，江西 景德镇 333000)

0 引言

准确性是工业机器人的重要性能指标。一般来说，几何误差[1]影响到总体定位误差，这些误差导致机器人定位精度[2]很低。提高定位精度可以通过运动学标定[3]，通常包含建模、测量、误差识别和误差补偿4个步骤。

本文在机器人运动学标定中同时考虑了连杆误差和运动副误差。为了避免不同参考点或线引起的误差，提出了一种基于离散点拟合运动轴线的方法确定转动副的固定轴和运动轴，根据轴线的相对位置确定杆长。以六轴喷釉机器人为例，利用辨识出来的轴线建立运动学模型，并对六轴机器人的位置误差进行了补偿。

1 六轴机器人的运动学模型

运动学模型的参数遵循D-H[4]方法。对于每个连杆i都有4个结构参数，当连杆坐标系建立后，这些结构参数也相应地被确定。六轴机器人D-H参数模型如图1所示，D-H参数表如表1所示。

图1 六轴机器人D-H模型

表1 六轴机器人D-H参数

其中d、a、α和θ分别表示连杆偏距、连杆长度、关节扭角和关节转角。

(1)

式中，θi为转动副的驱动参数。

2 六轴机器人运动学标定

2.1 离散位置的测量

以六轴喷釉机器人为例，测量一个运动副时，其他运动副锁定在初始位置。对于每个运动副，选择10个等间距的离散位置来确定轴线，以一关节为例，对于每个离散位置测量3个非共线的点以中心点为最终位置，对于离散的十点拟合空间圆并确定中心轴线位置。

根据以上步骤可以确定各关节轴线，利用式(2)计算各轴线的相对位置以确定机器人真实连杆长度。

(2)

式中，A表示轴线法向量，C表示中心点位置。

2.2 机器人的误差识别

分别测量由转动副R1、R2、R3、R4、R5和R6运动产生的末端连杆的离散点和测量坐标系下坐标系{OH；iH，jH，kH}的移动，末端连杆轨迹LF6(rPF6=[0，0，0]T)用以误差分析。选择一个圆形轨迹的10个位置，其标准位置方程为：

(3)

由于误差，轨迹的位置与标准位置不同。位置和姿态的偏差被认为是机器人的总误差，由关节臂坐标测量机测量。末端连杆轨迹的方向和位姿误差如图2所示。

图2 末端轨迹的位置与方向误差

结果表明：机器人的总误差主要是由连杆误差引起的，适当补偿连杆误差可以大大提高机器人的精度。与现有的识别方法相比，该方法基于每个转动副所产生的运动来识别轴线。因此，辨识模型与机器人的运动学模型无关，这提高了错误识别的效率，并且不需要为不同的D-H参数分配权重。

2.3 机器人的误差补偿

当连杆刚度足够大时，连杆误差是不会随着机器人载荷的变化而变化的。因此，基于所确定的参数，这些误差可通过机器人控制系统对杆长参数进行补偿。杆长识别前的参数a1、a2、a3、d4分别为50 mm、330 mm、50 mm、332 mm，补偿后a1、a2、a3、d4分别为49.83 mm、329.88 mm、50.39 mm、331.69 mm。

补偿前后离散点的位置误差如图3所示，用以误差分析的末端轨迹位置误差在补偿后极大地减小。补偿后依然存在的误差，大部分是由于运动副误差、载荷引起的重复位置误差和变形造成的。

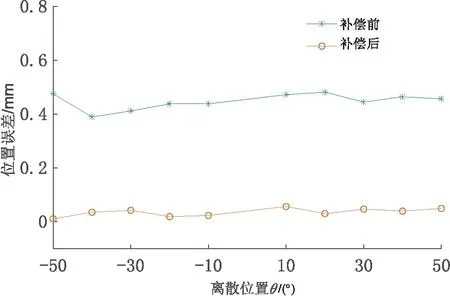
图3 补偿前后的运动误差

3 结论

本文提出了一种基于机构运动学的机器人运动参数识别方法，建立了包含运动副误差与连杆误差的机器人运动学模型，通过测量辨识出机器人运动副误差与连杆误差，并对喷釉机器人运动轨迹进行了补偿，试验结果表明了该方法的有效性，由此得出以下结论。

1)建立了包含运动副误差与连杆误差的机器人运动学模型。

2)通过关节臂坐标测量仪采集运动连杆轨迹，依次旋转单个运动副，通过单个运动副轨迹来辨识出单个运动关节的拟合轴线，然后求出相邻拟合轴线之间的DH参数完成连杆几何参数辨识。

3)将该方法应用于六轴喷釉机器人的运动学参数补偿。结果表明，机器人轨迹圆位置误差由0.445 4 mm降低到0.027 6 mm，机器人定位精度得到了提高。