上肢力量训练器低频抑振参数协调优化方法
胡孝海
(1.郑州大学体育学院,河南 郑州 450044;2.北京体育大学,北京 100084)
1 引言
人们生活质量不断提升,健身意识也随之加深,尤其是系统化健身。为了获取良好的健身效果,一般借助于某些健身器材来完成运动项目的训练。健身器材是对人体肌肉训练最有效的一种训练方式。其中,上肢力量训练器材是健身器材最重要的器材之一,对提升人体上肢力量具有至关重要的作用。使用上肢力量训练器材,可以有效锻炼身体上各块肌肉,能够增多肌肉纤维且促进毛细血管生成,使得上肢肌肉变得更加结实、发达,进而增强上肢骨骼的耐压、耐力以及耐扭的能力。但由于上肢力量训练器材长时间位于高速、负载的运行环境中,使得器材极易出现低频振荡[1]。为此,减少上肢力量训练器材的低频振荡情况,必须对其低频抑振参数进行协调优化。
文献[2]根据训练器材中阻尼转矩与电压稳定两者间的相互影响原理,利用自抗扰控制方式完成低频抑振参数协调优化,该方法有效缩短参数协调优化时长,但参数协调优化效果较差;文献[3]利用多频段稳定域方式搭建低频抑振参数协调优化模型,并通过遗传方法完成求解,该方法可以有效抑制低频振荡,但该方法的计算效率较低。
为此,提出了上肢力量训练器低频抑振参数协调优化方法。通过小波变换提取出低频抑振参数,可以缩短抑振参数提取时间;利用适应多运行方式构建低频抑振参数协调优化模型,提升抑振参数的适应性;运用免疫遗传算法进行协调优化计算,有效抑制低频振荡。
2 上肢力量训练器低频抑振参数协调优化分析
2.1 上肢力量训练器低频振荡检测
采用经验小波变换,检测上肢力量训练器低频振荡。设定{(xi,yi),i=1,2,…,m} 表示大小是m的上肢力量训练器材低频振荡检测样本,该样本由两种数据构成的,若xi属于第一种,则yi=1;xi属于第二种,则yi=-1。若ωx+b=0表示低频振荡检测超平面,则把上肢力量训练器材低频振荡样本分成两种,就必须符合式(1)条件。

低频振荡检测[4]的最大化间距是指该检测超平面和实际平面上,全部低频振荡样本的最小极值,即为该器材的低频振荡分类线的最佳解,如式(2)所示。

式中:ai—经验小波变换乘子。
在低频振荡检测的实际运用中,低频振荡均是非线性的,若分类结果不能符合要求,就需要将非线性变换成容易处理的线性问题[5]。训练器材低频振荡检测模型在处理此问题过程中,需要将低频振荡的目标函数Q(a)进行转化,如式(3)所示。

通过式(3)可知,利用经验小波变换搭建上肢力量训练器材低频检测模型,如式(4)所示。

式中:K(xixj)—搭建低频振荡检测模型所利用的核函数;b—偏置数值。
通过式(3)将低频振荡样本划分为两种,获得低频样本划分条件,并利用低频分类线的最佳解,完成低频振荡目标函数的变换,并通过式(4)建立低频振荡检测模型。下面通过低频振荡模型,提取上肢力量训练器材低频抑振参数。
2.2 低频抑振参数提取
在低频抑振参数提取流程中,设定s(n)表示低频振荡采样集合中点n的输出信号,根据p个检测输出信号s(n-1)+s(n-2)+…+s(n-p)的线性组合,如式(5)所示。
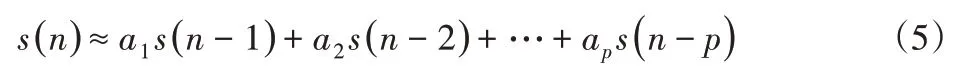
为了能够让输出信号s(n)的两边等同,在式(5)右边尾项增添一项,如式(6)所示。
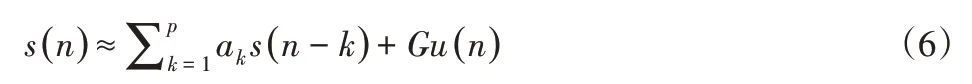
式中:ak—函数方程的比例参数;G—低频振荡检测的增益系数;u(n)—检测响应时长;Gu(n)—G、u(n)的乘积结果。利用经验小波变换[6]得出检测信号成分,并将式(7)映射到z区域范围内,得出:

通过式(7),即可得出上肢力量训练器材低频振荡检测的传输函数模型,如式(8)所示。
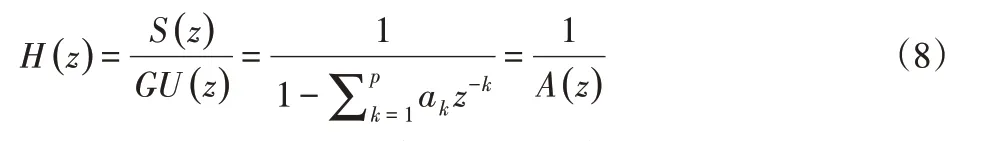
式中:H(z)—由p个低频抑振参数决定的传递函数。
尽管低频抑振参数不断发生改变,极难确定,但使用经验小波变换可以将波动数据压缩,使检测样本的点和压缩后的点进行拟合,获得一个近似的数值。该过程会得出一个近似的数值,导致得出结果与实际存在较大的误差,为此使用来表示,如式(9)所示。

为了得出低频抑振参数的估计数值,使用经验小波变换的伸缩因子形成不同的频率成分的特征,在参数提取流程中,设定起点为n终点为m的短时低频信号和误差信号的表达式,如式(10)、式(11)所示。

当sn(m)和en(m)在尺度、小波的空间相互正交过程中,获得低频抑振参数提取误差的平均和,如式(12)所示。

现阶段,利用小波分解树二次分解将近似分量环节的参数进行处理,进而提取出低频抑振参数,如式(13)所示。
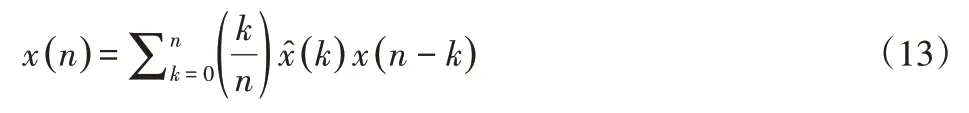
因为低频振荡检测终端输出信号的线性组合不能确保低频信号两边完全等同,在输出信号的右边尾项增添一项,采用经验小波变换获得该信号成分,并构建传递函数,通过低频信号和误差信号,完成上肢力量训练器材低频抑振参数提取。
2.3 低频抑振参数协调优化
2.3.1 低频抑振参数协调优化数学模型搭建
为了更好地对低频抑振参数进行协调优化,首先采用适应多运行方式搭建低频抑振参数协调优化数学模型,并利用免疫遗传运算完成求解。
上肢力量训练器材低频抑振协调优化的目的是得出低频抑振的最优参数,使在各种工作状态下,低频部分的最小阻尼比[7]均能达到极大数值,如式(14)所示。
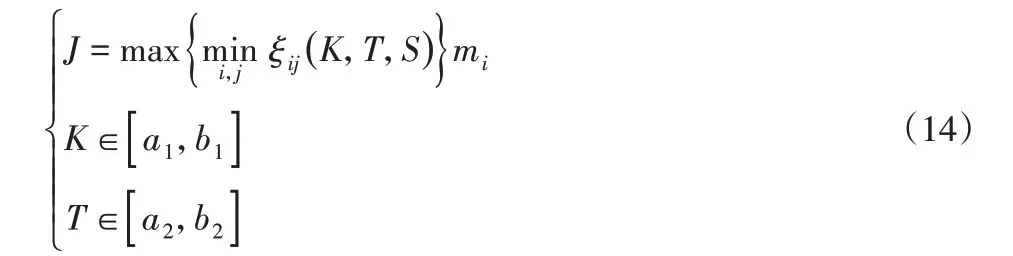
式中:下角标i—第i种运营模式;j—第i种运营模式下第j个低频振荡形式;mi—第i种运营模式下的低频振荡形式数量;ξij—第i种运营形式下第j个低频振荡形式的阻尼比;向量K、T分别代表低频抑振设备的放大倍数参数向量与时长参数向量;a1、b1和a2、b2分别表示该放大倍数参数向量与时长参数向量的两个最大值和最小值。
因为上肢力量训练器材中每个协调系统函数方程、负载函数方程、网络运行函数方程以及输电系统函数方程共同构成系统的线性微积分代数函数方程,并消除代数变量[8],完成低频抑振参数协调优化数学模型搭建。其中,整个系统的线性微积分函数方程,如式(15)所示。

式中:A—该系统状态函数方程的参数矩阵。
2.3.2 协调优化
为了解决上肢力量训练器材参数协调优化过程存在的局部极值问题[9],采用免疫遗传方法对其进行协调优化,详细过程如下:
(1)抗体
抗体包含二进制、十进制两个部分,其中,二进制表示为低频抑振设备的安装位置,即S(用1、0分别表示已安装位置与不需要安装),而十进制部分代表低频抑振的参数K、T。在参数协调优化时,根据PSS、SVC、SVG、TCSC、TCPS的次序依次编码。
(2)抗体评价
抗体的期望数值

式中:Pf(v)—抗体适应程度;Pd—抗体浓度。
在对抗体评价过程中,适应程度越高、浓度越低的抗体生成后代的概率越高。这里通过抗体的由好到差序号重新分配,分配序号越小表明抗体分配性能越强,低频抑振越佳,该过程,如式(17)所示。

式中:i=1—对应最佳的染色体;i=n—对应最差染色体。a*—适应度函数方程的比例参数,这里取经验数值为0.06,则浓度反比例函数,如式(18)所示。

式中:C(v)—抗体浓度;α、β—均为常数,通过反复测试,得出平均值为1。
(3)抗体变异
因为抗体混合编码过程中也会出现二进制与十进制交叉变异。二进制部分与一般遗传方法等同,而十进制部分的交叉根据式(19)得出的。

c—(0~1)范围内任意数值。

式中:r—(0~1)区间分为内任意数值;T—极大遗传代数;H—迭代数依赖程度的系统参数,这里H取值为10。
(4)抗体动态变化
交叉、变异概率动态变化,如式(21)、式(22)所示。

3 实验结果分析
为了验证所提上肢力量训练器低频抑振参数协调优化方法的有效性,实验在PSD-BPA软件中进行,且上肢力量训练器材的发动机选用二阶全局模型,上肢力量训练器,如图1所示。实验在上肢力量训练器中任意选择两种运行模式,分别计算所提方法、文献[2-3]方法的系统频率振荡阻尼比与低频振荡模式最小阻尼比值,如表1所示。

图1 上肢力量训练器Fig.1 Upper Limb Strength Training Device

表1 参数协调优化下系统阻尼比对比结果Tab.1 Comparison Results of Damping Ratio of the System Under Coordinated Optimization of Parameters
通过表1可以看出,对于初始参数,文献[2]方法能够有效提升振荡阻尼比,但低频振荡最小阻尼比提升较差,文献[3]方法可以提升低频振荡最小阻尼,但提升振荡阻尼比较弱,而在所提方法参数协调优化系统下,频率振荡阻尼比与低频振荡最小阻尼比均得到有效的提升,因为所提方法使用适应多运行方式,可以在多种运行模式下调节阻尼比,使低频振荡得到有效抑制,同时还能提升振荡的阻尼比。对上肢力量训练器系统进行时域模拟仿真,得到两种运行模式下频率振荡变化对比结果,如图2所示。

图2 两种运行模式下频率振荡变化对比结果Fig.2 Comparison Results of Frequency Oscillation Changes in Two Operating Modes
图2中,(0~2)s为初始频率振荡,(2~8)s为加入低频振荡后频率变换情况,(8~20)s为三种参数协调优化方法得出频率变化情况。通过这两种运行方式均能看出所提方法得出频率峰值均低于文献方法,因为所提方法使用线性微积分代数函数,建立低频抑振参数协调优化数学模型,可以对各种模式下低频抑振参数进行协调优化,有效抑制低频振荡,具备极佳的学习、记忆以及自适应协调能力,为此所提方法低频抑振参数协调优化效果较好。在此基础上,进一步验证所提方法的参数协调优化方法性能,得到三种方法的收敛速度对比结果,如图3所示。由图3可知,所提方法的低频振荡收敛速度较快,同时,在收敛时长上所提方法使用时间最短,计算效率较高。因为所提方法使用经验小波变换方式,提取的低频抑振参数均为有效参数,为参数协调优化计算节省大量时间,为此,在相同模式环境下,所提方法能够有效提高收敛速度和计算效率。

图3 三种方法的收敛速度对比Fig.3 Convergence Speed Comparison of the Three Methods
4 结论
这里提出的上肢力量训练器低频抑振参数协调优化方法,采用经验小波变换和免疫遗传方法,搭建多种运行系统的低频抑振参数协调优化模型,实现低频抑振参数协调优化。研究结果如下:(1)所提方法的低频抑振参数协调优化效果较好,能够有效提升上肢力量训练器材安全性。(2)所提方法可以在多种运行模式下,协调优化低频抑振参数,从而有效抑制低频振荡。(3)所提方法解决了参数协调优化过程中存在的局部极值问题,提高了收敛速度和计算效率。

