城市非信控多交叉路口多车协同控制方法*
于杰 江发潮 孔伟伟 罗禹贡
(1.中国农业大学,北京 100083;2.清华大学,北京 100084)
主题词:多性能目标优化 模型预测控制 车路协同控制 多车协同控制 非信控多交叉路口
1 前言
随着城市化进程的加快,城市多交叉路口交通系统的管理变得越来越重要[1-2]。同时,新一代信息通信技术使得智能网联汽车能够有效地提升安全性和交通通行效率,将为道路交通系统的管理带来巨大的挑战和机遇。因此,协同考虑交通系统的整体性能优化、充分发挥智能网联汽车的优势,对交通效率和车辆经济性的提升具有重要意义。
目前,非信控交叉路口车-车协同控制方法主要包括集中式控制方法和分布式控制方法:集中式控制方法是指存在某一交叉路口控制单元,其收集交叉路口区域所有车辆的信息,并进行全局优化,进而为每一辆车分配通行次序[3]、到达时间[4]或者通行轨迹[5]等;分布式车-车协同控制方法是指车辆的控制指令并非是在获取全局信息后进行规划的,而是由车辆依据通信系统所获取的局部信息确定的,在这种情况下,利用车-车通信技术,与其他车辆协同完成交叉路口通行任务[6-7]。
但城市场景通常是由多个相互连接的交叉路口组成,针对非信控多交叉路口场景,Chairit Wuthishuwong等[8-9]采用离散时间一致性算法来协调交叉路口与其邻近区域的交通密度,以提高每个交叉路口的交通流量。Du等[10-11]针对2个相邻交叉路口场景,通过评估道路期望平均速度,并根据与当前速度的最小偏差和交叉路口处的避碰来为每辆车分配最佳参考速度,从而提升车辆燃油经济性。综上所述,针对多交叉路口多车协同控制方法:在宏观交通层面,现有研究主要从交通管理角度考虑如何改善道路通行效率与车辆燃油经济性,但未涉及车辆本身的动态特性所带来的能耗影响;在微观车辆层面,通常从车辆控制角度考虑了前车或交通流等对车辆燃油经济性的影响,但较少考虑多交叉路口间的车辆调度对通行效率的影响。因此,现有研究尚缺乏综合实现宏观层面的道路通行效率和微观层面的车辆燃油经济性协同优化的相关研究。
本文针对现有研究的不足,提出一种面向城市环境多交叉路口多车协同的多层递阶分布式协调控制方法,旨在实现从宏观交通和微观车辆2 个层面提升交叉路口的通行效率和燃油经济性。
2 多层递阶分布式协调控制架构设计
本文的研究场景如图1所示,为由多个交叉路口和路段组成的道路网络。每个交叉路口子区域分别划分为2 个区域,即路口区域和路段区域。在路段区域内,车辆在路段上跟车行驶,实行一维车辆队列控制;在路口区域内,车辆则调整其运动,排除各向交通流间存在的时空轨迹重叠,进而消解潜在冲突,实现二维车群协调控制。

图1 研究场景
针对智能网联汽车在非信控多交叉路口的通行问题,本文提出一种多层递阶分布式协调控制架构,如图2 所示,包括宏观交通优化层和微观车辆队列控制层。在宏观交通优化层中,根据交叉路口子区域i和交叉路口子区域j的交互交通流量Qij和交叉路口子区域i的期望道路均衡流量Qi,构建各交叉路口子区域控制器。在微观车辆队列控制层中,根据上层获得的车辆最优行驶速度及各车辆位置等信息,构建各车载控制器(包括队列头车控制器和跟随车车载控制器)。

图2 多层递阶分布式协调控制架构
各交叉路口子区域控制器针对每一个非信控交叉路口,利用车辆与基础设施(Vehicle to Instruction,V2I)之间的通信技术接收车辆运动信息,以各交叉路口子区域所有车辆的车速Vi、位置Si和车辆数量Ni为输入,基于多交叉路口中路段和路口车辆几何拓扑,根据道路期望均衡流量和各子区域间的交通流量,构建考虑宏观交通流预测模型、安全约束等约束条件以及综合交通效率、交通一致性等多性能目标的集中式模型预测控制器,并完成多性能目标协同控制问题中的权重系数优化,集中优化参考速度输出,实现在宏观交通层面管理各交叉路口,提升各交叉路口通行效率和通行车辆的经济性。在各交叉路口,以提高所有车辆安全性和交通效率为目标,通过旋转投影的方法将交叉路口不同入口车道的车辆队列投影到虚拟车道上并构成虚拟队列,从而实现各车辆通行次序分配,组织车辆有序通过路口;此外,在各路段区域,通过车辆与车辆(Vehicle to Vehicle,V2V)之间的无线通信技术共享运动信息,各车载控制器根据邻域车辆的速度vi和位置si信息控制车辆的运动,完成多车系统队列行驶。
在各车载控制器中构建以车辆稳定性、舒适性和经济性等多性能目标函数,以及考虑车辆非线性动力学预测模型、车辆安全跟车约束、车辆运动学约束等约束条件的分布式模型预测控制器,根据各交叉路口子区域控制器分配的最优参考速度,优化车辆动力学输入,实现在微观车辆层面上多交叉路口环境下的车辆行驶安全性和经济性等多性能的综合提升。
3 宏观交通优化控制方法
3.1 交通控制模型建立
宏观交通流模型[12-13]能够精确地反映交通流的动态特性,因此采用宏观交通流模型作为本文的交通流模型,根据车辆守恒定律,有:
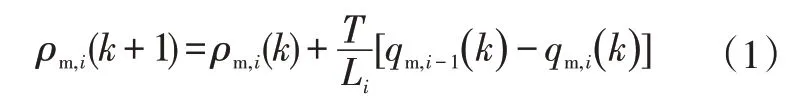
式中,ρm,i(k)、qm,i(k)分别为k时刻编号为i的路段的平均密度和流量;T为采样周期;Li为编号i的路段长度。
动态速度经验方程为:

流量方程为:

3.2 交叉路口子区域多性能目标控制器设计
城市多交叉路口系统是一种多输入多输出的动态高维复杂不确定性系统,并且随着交叉口规模的增大,优化问题的复杂度呈指数增长,为有效引导交通流,减少交通拥堵,采用网络化分布式控制策略,基于集中式优化和分布式控制架构对协同控制模型进行分层解耦,降低优化控制系统维度。将多交叉路口划分为多个子系统,每个子系统由1 个子区域控制器控制,并且每个子区域控制器通过求解1 个低维的优化问题获得对应子系统的控制量,从而实现通过提供子区域之间的最优平均交通速度,并将其作为各车载控制器的参考目标。此外,由于每一个子区域并不是独立存在的,若不考虑子区域之间的协调关系,求得的各子区域的最优解为局部最优,未达到全局最优。因此,为解决子系统之间的协调问题,将整体问题分解为利用局部信息的子问题,在每一步迭代中,每个交叉路口子区域控制器通过获得其相邻交叉路口子区域上、下游的实时动态信息,协调多个交叉路口的决策过程,实现多交叉路口的一致性控制,进而提升整个系统的性能。
考虑将多交叉路口划分为数量为i(i∈N)的子网络,该子系统优化问题描述为:

考虑到交通系统是真实的物理系统,各子区域间的最大交换流量等必须受到一定的约束,设计4个约束保证交通系统的稳定性,分别是速度约束、流量约束、相邻子区域间的交互交通流量约束、车流量守恒方程约束。
经过上述控制问题的建立,基于宏观交通流模型,得到了非线性约束优化问题,在该系统中的每个子区域上都定义一个子预测优化问题,每个子预测优化问题只利用邻域及期望信息进行优化求解,得到该子区域交叉口控制器的控制输入,已知系统中存在N个交叉路口,即为N个子预测优化问题,在每一个子预测优化问题中预测步长均为Np,其预测序列都是在每一个预测时域[t,t+Np]内的序列,每一预测序列中,k=0时刻的状态值为t时刻的系统测量值,以每一时刻的系统测量值为起点进行预测序列的计算。
4 微观车辆队列优化控制方法
4.1 车辆队列控制模型建立
车辆模型具有强非线性特性,为保证车辆队列行驶的稳定性及其每辆车在队列中的跟车性能,需在控制过程中考虑车辆纵向动力学方程中的非线性项,队列单车动力学方程描述为[15]:

式中,i={1,2,…,N}为车队内车辆的序号;si(t)、vi(t)分别为车辆i的位移和速度;mi为车辆i的质量;Tq,i(t)为车辆i实际驱动/制动力矩;ui(t)为车辆i期望驱动/制动力矩;ηm,i为车辆i传动系统机械效率;τi为车辆i纵向动力系统时滞系数;i0,i为车辆i机械传动比;rw,i为车辆i车轮滚动半径;CD,i为车辆i空气阻力系数;Ai为车辆i迎风面积;ρ为空气密度;f为车辆的滚动阻力系数;g为重力加速度;α为道路坡度。
设离散时间步长为Δt,则上述连续的非线性状态方程离散后为:

式(6)可进一步写成:

从而,队列系统输出为:

式中,γ=diag(1,1,1)。
将上述单车动力学方程集成写为队列整体的总状态形式,设车辆队列的状态方程为:

由此建立车辆队列非线性动力学模型,为后续队列控制器的设计提供基础。
4.2 车辆队列多性能目标控制器设计
道路上行驶的车辆并不是孤立的个体,而是与其他车辆耦合成一个车群系统。在车群系统中,车辆-道路等要素之间相互制约,构成一个复杂的广义动力学系统。根据四元素模型[16],将级联的队列系统分解为局部解耦的子系统,通过跟踪各路口子区域控制器发送给各队列领航车子系统的最优速度信息,采用分布式模型预测控制(Distributed Model Predictive Control,DMPC)[17]对每个子系统设计了稳定的分布式控制器,将车辆队列问题视为分布式多节点的优化控制问题,实时优化车辆速度,实现微观车辆层面经济性提高等。本文建立控制问题描述为:

式中,J1,i(k|t)=||W1,i(yides(k|t)-(k|t))||2为自车与领航车之间的跟车误差目标函数,yides表示自车的期望位置;W1,i为自车与领航车的误差系数矩阵;i为自车编号为系统预测输出;J2,i(k|t)=||W2,i(yj(k|t)-(k|t))||2为自车与前车之间的跟车误差目标函数;W2,i为自车与前车的跟车误差权重系数矩阵为前车的期望状态;d为跟车距离为自车的控制量与车辆匀速行驶时转矩的误差,即舒适性目标函数;W3,i为舒适性权重系数矩阵;J4,i(k|t)=||W4,i为稳定性目标函数;W4,i为稳定性权重系数矩阵(k|t)为车辆预测输出序列(k|t)为车辆通过通信拓扑结构向编队系统中其他车辆传输的序列;vmin、vmax分别为多车系统的最低、最高车速;Tmin、Tmax分别为自车电机能够达到的最小、最大转矩;ddesire为期望安全车距;分别为领航车向队列传递的纵向车速和位移信息为车辆以最优速度行驶过程中的转矩:

在建立控制器终端约束中,设计3个终端约束保证车辆行驶的稳定性,首先设计车辆在预测终端时保证预测终端车速与领航车车速相同,其次设计车辆预测终端的位移同自车与领航车的期望位移一致,最后设计车辆预测终端转矩与车辆匀速行驶时的车辆平衡转矩相同。
5 仿真验证
本文采用MATLAB 与城市交通仿真(Simulation of Urban MObility,SUMO)[18]软件构成联合仿真环境。构造了4×4 的典型多交叉路口作为测试场景,如图3 所示,共包含12 个交叉路口(拐点处的路口可认为是路段)和44个路段,其中十字交叉路口4个,丁字交叉路口8个,设置仿真场景中相邻交叉路口的距离均为200 m。

图3 仿真测试场景示意
在设置的交通仿真场景中,通过采用传统队列控制方法作为基准算法与多交叉路口宏观交通-微观车辆协同控制方法进行仿真对比,记录和输出车辆运动信息,并采用相同的车辆模型分别计算N2~N13交叉路口子区域(N1 与N14 为出入口区域,不需计算)交叉路口的平均行程时间、平均速度和平均燃油消耗量,作为算法对比的性能指标,对比结果如图4~图6 所示,3 次仿真统计结果平均值如表1所示。

表1 仿真统计结果
结合图4~图6 可以看出,仅采用队列控制基准算法,在未考虑多交叉路口智能网联汽车多车协同的条件下,在第250~300 s,交叉路口子区域4、交叉路口子区域5、交叉路口子区域6、交叉路口子区域9、交叉路口子区域10等区域已经出现严重拥堵,车辆能耗快速增加,道路平均速度明显降低,并且随着时间的增长,道路已达到通行能力饱和水平,各交叉路口子区域路段已产生排队等问题,随着排队车辆的增多,交通拥堵的趋势会加剧,在极端情况下甚至会导致整个交通系统的失衡。


图4 交叉路口子区域平均行程时间
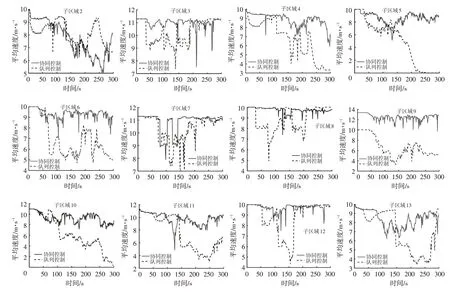
图5 各交叉路口子区域平均速度


图6 各交叉路口子区域平均燃油消耗量
相较于采用基准算法控制的车辆,采用协同控制方法控制的车辆,除在交叉路口子区域3、交叉路口子区域8 等,部分车辆进入子区域时由于车辆队列发生调整,导致能耗较高外,其余子区域由于车辆密度的分布更为均匀,随着时间的增长,未出现交通拥堵状况,可有效缩短平均行程时间和提升车辆平均速度,实现在显著提升多交叉路口通行效率的同时,降低车辆能耗。
由表1对比结果可以看出,在保证车群通行安全的前提下,采用所提出的方法能够缩短平均行程时间约57.99%,提升平均速度约29.76%,同时降低约13.66%的能耗,实现了从宏观交通和微观车辆2个层面同时提升道路交通效率和车辆燃油经济性的目标。
6 结束语
本文提出了一种面向城市非信控多交叉路口多车协同的多层递阶分布式协调控制方法,通过构建各交叉路口子区域宏观交通和智能网联车辆队列的控制模型,解决了宏观层面道路通行效率和微观层面车辆燃油经济性的协同优化问题。
本文采用模型预测控制方法针对每个交叉路口子区域的通行效率、交通流量一致性等多性能目标,实现了宏观交通层面的集中式优化控制,并通过分布式模型预测控制方法针对车辆队列安全性、经济性等多性能目标,实现了微观车辆层面的分布式优化控制。
仿真结果表明,在设计的包含12 个交叉路口的典型非信控交叉路口场景下,所提出的方法能够在保证车群通行安全的前提下,缩短平均行程时间约57.99%,提高平均速度约29.76%,同时降低约13.66%的能耗,有效提高了交通通行效率和车辆经济性。

