用折合质量法解答2022年高考全国乙卷第25题

江西 聂应才 应强强

2022年高考已落下帷幕,对高考试题的分析是一线教师研究命题规律、把握考向的重要手段。笔者用折合质量法分析了2022年高考全国乙卷理综物理压轴题,提出复习课不是重复再现,而是深度再学习过程,以供借鉴。

1 引言

(2022·全国乙卷·25)如图1,一质量为m的物块A与轻质弹簧连接,静止在光滑水平面上;物块B向A运动,t＝0 时与弹簧接触,到t＝2t0时与弹簧分离,第一次碰撞结束,A、B的v-t图像如图2所示。已知从t＝0到t＝t0时间内,物块A运动的距离为0.36v0t0。A、B分离后,A滑上粗糙斜面,然后滑下,与一直在水平面上运动的B再次碰撞,之后A再次滑上斜面,达到的最高点与前一次相同。斜面倾角为θ(sinθ＝0.6),与水平面光滑连接。碰撞过程中弹簧始终处于弹性限度内。求:

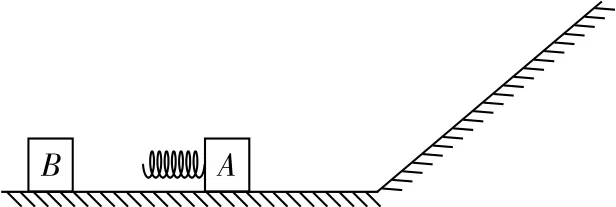
图1

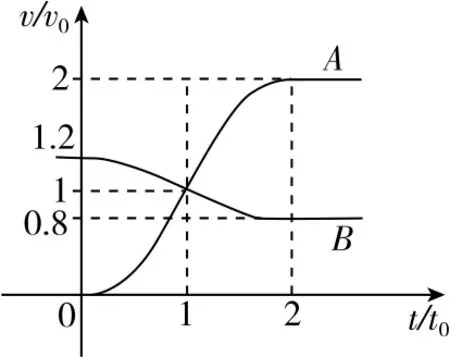
图2

(1)第一次碰撞过程中,弹簧弹性势能的最大值;

(2)第一次碰撞过程中,弹簧压缩量的最大值;

(3)物块A与斜面间的动摩擦因数。

2022年高考全国乙卷理综物理压轴题第25题,实质是二体问题。对于这种问题,如果在地面参考系与A(或B)参考系间切换,则科学思维更流畅、方程更简捷、计算更简化、解答更明了,会使问题变得十分简单;但在以A(或B)为参考系时,需要将另一物体B(或A)的质量进行折合,两质点质量分别为m1、m2,则其折合质量μ＝。下面笔者运用折合质量法进行解答。

2 解答过程

2.1 质点系的动能——柯尼希定理

Ek＝为S系中质心的动能,得出S系中质点系的动能可视为质心动能与S′系中质点系的动能之和,即著名的柯尼希定理。

第3问与第1问都是能量关系问题,解决了第1问,接着思考第3问。第一次碰撞后,物块A以2v0速度沿斜面上滑,假设上滑最大路程为s,由动能定理得

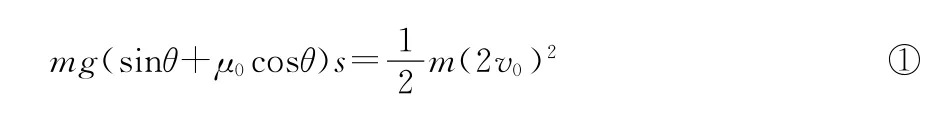
设物块A下滑离开斜面时速度大小为v,同理

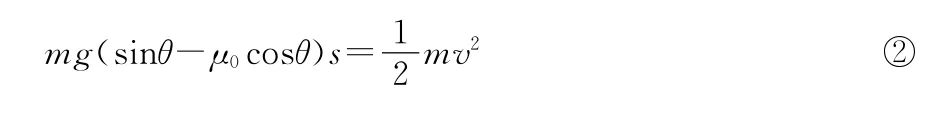
物块A以速度v向左运动,与以速度0.8v0向右运动的B相互作用,作用结束,B速度变为vB,因A到达的最高点和前一次相同,则A仍以2v0速度沿斜面上滑。取向右为正方向,由动量守恒定律得

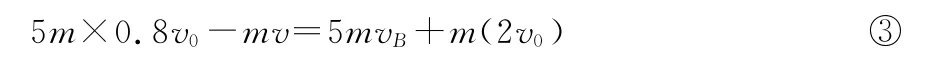
A、B作用过程是资源动能与弹簧弹性势能间的转化,有

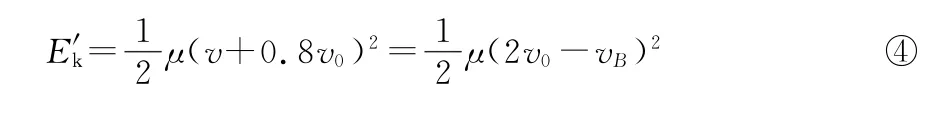
③④联立,解得vB＝0.2v0,v＝v0

将数据代入②式,并结合①式,解得物块A与斜面间的动摩擦因数μ0＝0.45。

2.2 相对运动的牛顿运动定律

两质点在运动过程中,如果以其中某个质点作为参考系,另外质点的牛顿第二定律是f＝μaμ,式中f是质点间的作用力,μ是折合质量,aμ是折合加速度,即它们的相对加速度。根据折合质量概念,可直接用牛顿运动定律讨论任何二体问题的相对运动,而无需考虑惯性力。第一次碰撞过程中,以地面为参考系,某时刻A的加速度为aiA ＝,方向向右;B的加速度为aiB ＝,方向向左。

在0～t0时间内,A的 位移

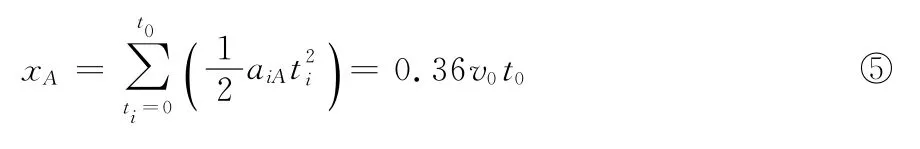
以A为参考系,0～t0时间内,B的位移即为弹簧压缩量的最大值,相对初速度是1.2v0,方向向右;折合加速度aiμ ＝aiA ＋aiB ＝,方向向左。B相对于A做减速运动,相对位移

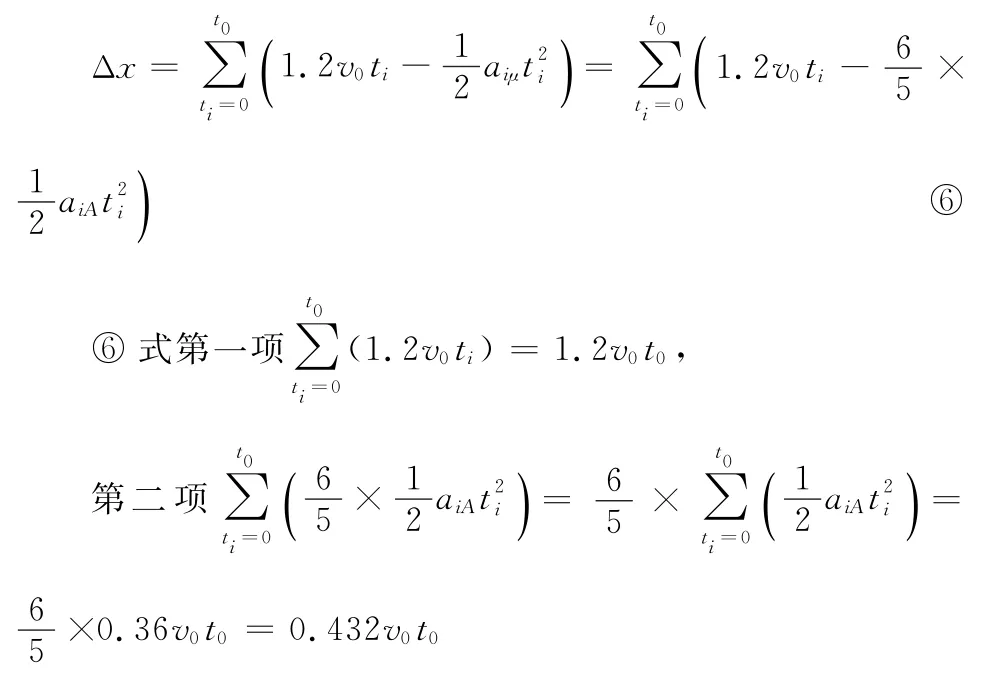
解得Δx＝1.2v0t0－0.432v0t0＝0.768v0t0。这就是第一次碰撞过程中,弹簧压缩量的最大值。

3 教学启示

3.1 拓展知识,发展思维

教学的重心不只是知识的传授,以知识为载体,提升学生核心素养才是关键,而科学思维又是物理素养的核心,发展思维,才是以不变应万变的策略。发展思维的有效路径之一是要善于延伸拓展知识,不拘泥于教材。我们不妨对此题再次进行深入挖掘。

【拓展1】弹簧弹性势能的表达式Ep＝,式中k是弹簧的劲度系数,x为弹簧的形变量。求物块A、B第二次与第一次碰撞过程的弹簧压缩量最大值之比。

第二次碰撞过程中,A、B的资源动能为(v＋0.8v0)2＝,因此这次弹簧弹性势能最大值为,则第二次与第一次弹簧压缩量最大值之比为

【拓展2】求弹簧的劲度系数k的表达式。

从0～2t0时间内,以物块B为参考系,物块A在平衡位置(弹簧原长处)以速度1.2v0向左压缩弹簧,在t0时刻,弹簧最短,A速度为零,然后反弹,2t0时刻回到平衡位置,速度是1.2v0,方向向右,整个过程做简谐运动,周期T＝4t0。由简谐运动周期公式T＝,解得弹簧的劲度系数

【拓展3】物块A和B用此弹簧相连,放在水平台面上。弹簧自然长度为l0,A、B与水平台面的动摩擦因数均和A与斜面间的动摩擦因数相同,现将它们拉开距离l,同时由静止释放,求弹簧第一次回到自然长度时,两物块的相对速度。

如此变式拓展训练,进一步夯实了学生的运动与相互作用观念、能量观念等物理观念,同时提升了模型建构、科学论证和科学推理等科学思维素养。

3.2 再度审视,进阶学习

高中物理知识点近160个,核心知识20多个,高考内容集中在这些核心知识中,为了提高熟练程度,许多学校在高考复习期间安排学生做了大量习题,为遏制刷题内卷,高考试题总是“出乎意料”,提醒教师应该提炼物理概念和规律,从新课需要的视角进行复习。学习进阶是对学生在各阶段学习同一主题的概念时所遵循连贯的、典型的学习路径的描述,一般呈现为围绕核心概念展开的一系列由简单到复杂、相互关联的概念序列。复习不是重复,而是进阶学习。

微元法渗透在不同知识板块中,着重化“变”为“不变”的物理思想,然后在“不变”的基础上连续求和的方法,⑤⑥式借用数学语言表达微元求和,是对它的一种提炼升华。新课处理双星问题时,通常引导学生理解轨道半径与星体间距离关系,角速度、周期、线速度等关系,列几个方程来求解,但如果以其中一颗星体作为参考系,就转化成了常规的行星运动模型,其质量就要用折合质量代替。折合质量法处理双星体将会“别有风味”。

4 结语

二体问题引入折合质量,质心运动不变,相对运动产生的资源动能是系统内机械能与其他能转化的总量,可以迅速转化为其他能的极值;动力学方程不用考虑是否为惯性系,将质量换算成折合质量,列式与以地面为参考系的牛顿运动定律一样。如此思考就简单明了了。

高考承担着“立德树人、服务选才、引导教学”功能,高考试题对一线教学发挥着积极的指导作用,复习不仅是要做题,更要发展学生科学思维,对于相同知识内容,不同阶段要作不同深度、广度的高阶思维学习,不能仅是重复再现。