2022年高考全国甲卷第18题再思考

广西 孙会刚 李晓晨

全国甲卷试题注重内容的基础性,突显了对学生能力的要求,实现了高考对学生“一核、四层、四翼”的考查,本文就2022年高考全国甲卷第18题进行分析,以飨读者。

一、真题展示

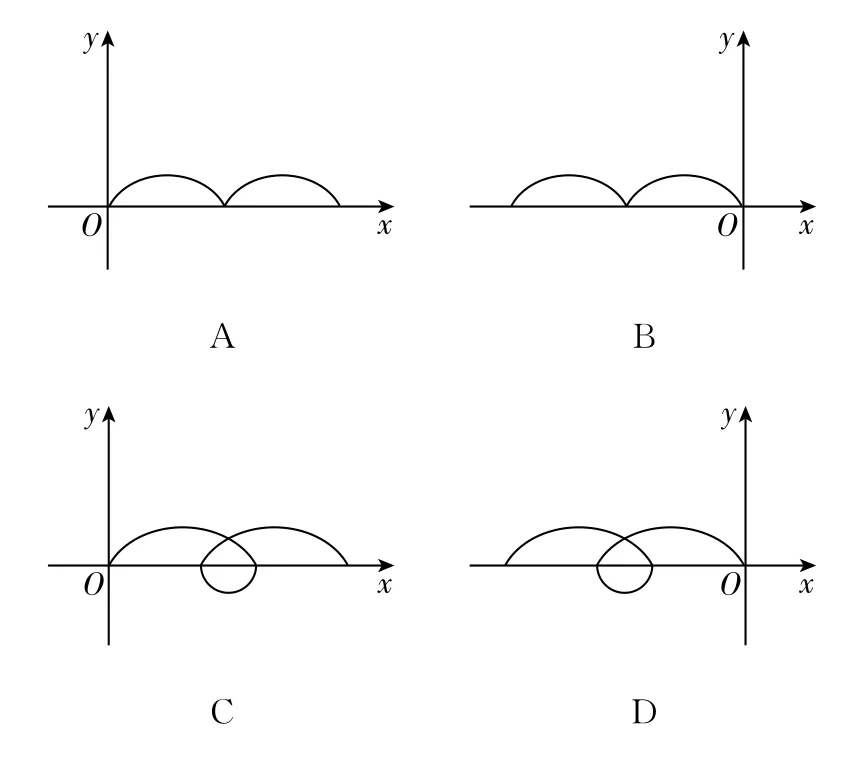
空间存在着匀强磁场和匀强电场,磁场的方向垂直于纸面(xOy平面)向里,电场的方向沿y轴正方向。一带正电的粒子在电场和磁场的作用下,从坐标原点O由静止开始运动。下列四幅图中,可能正确描述该粒子运动轨迹的是 ( )

笔者将采用多种方法,层层深入,系统解决此类复合场问题。

1.定性分析找出轨迹图

由题干可知,带电粒子受到沿y轴正方向的电场力,从坐标原点O由静止开始沿y轴正方向加速,同时运动的带电粒子还会受到沿x轴负方向的洛伦兹力,使带电粒子向着x轴负方向偏转。当粒子再次经过x轴时,由于洛伦兹力不做功,只有电场力做功,由动能定理可知,粒子速度恰好减为零,不会存在穿过x轴的现象,故B选项正确。

上述定性分析只能得出带电粒子大致的运动轨迹,但仍不知道这个轨迹是什么曲线,同时也不能对粒子的相关物理量进行定量计算。

2.定量计算求出极值

设电场强度为Ej,磁感应强度为－Bk,带电粒子的电荷量和质量分别为q、m,任意t时刻粒子的速度设为vi ＝vixi＋viyj,其受到的洛伦兹力可表示为F ＝－qviyBi＋qvixBj,由动量定理有

当粒子偏离x轴最远时,vy ＝0,此时粒子速度达到最大,设为vm,则上述结果可化为

由于只有电场力做功,根据动能定理得

显然题中x,t的关系未知,无法求得达到速度极值所用时间和对应的位移。分析发现,ym＝可改写为ym＝,正好是粒子以速率在磁场中做圆周运动的直径,则粒子的轨迹应该和圆周运动有关。

3.配速法寻找轨迹方程

假设粒子在坐标原点O处具有一对大小相等、方向沿x轴 相反的速度v0,其中沿x轴负方向的速度v0获得的洛伦兹力用来平衡电场力,以保证粒子受到的合外力仅为一个洛伦兹力,则有qv0B ＝qE,即v0＝。

此时由于粒子受到沿y轴负方向的洛伦兹力与电场力平衡,从而沿x轴负方向做匀速直线运动,同时沿x轴正方向的速度v0i获得洛伦兹力使其做匀速圆周运动,其半径和周期分别为r＝。故粒子的两个分运动分别为沿x轴负方向的匀速直线运动和速率为v0的匀速圆周运动。

其对应的轨迹方程为

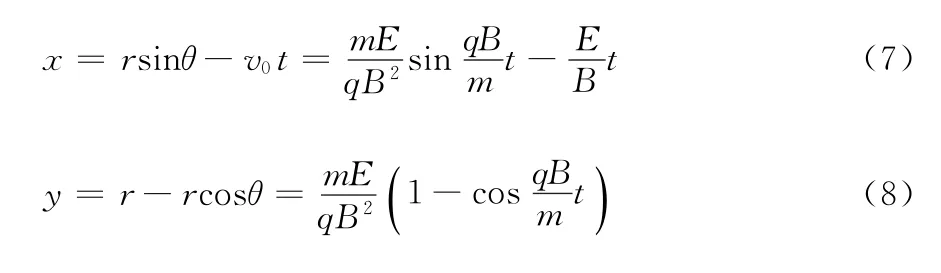
以θ为参数可化为x ＝r(sinθ－θ),y＝r(1－cosθ),此方程为滚轮线方程,其图像如图1所示。

图1

通过上述分析可定量求出粒子第一次达到最大速度时,做匀速圆周运动的分运动恰好转动半个圆,使得两个分速度恰好同向,则vm＝2v0＝,ym＝2r＝,与用动量定理计算结果完全一致。同时,我们还可以求出粒子第一次达到最大速度时经历时间为t ＝,坐标为。值得注意的是,在这个运动过程中,速度达到极值时粒子的受力并不平衡,且速度方向与电场力方向垂直。这一点是帮助学生纠正固化思维的一个难得的教学点。

配速法不仅巧妙地解决了粒子的运动轨迹,将复杂的运动分解为两个简单的分运动,使学生对粒子的运动过程有了全面地了解。那么有老师或学生会问,这个配速法会不会存在逻辑上的不足?如果粒子在O点已有速度,那么粒子的轨迹又应该如何?速度对轨迹有何影响?

4.建立微分方程,定量求得一般情况下粒子的轨迹

设粒子在O点时的速度为v0＝vx0i＋vy0j＋vz0k,任意t时刻粒子的速度设为v ＝vxi＋vyj＋vzk,其满足方程

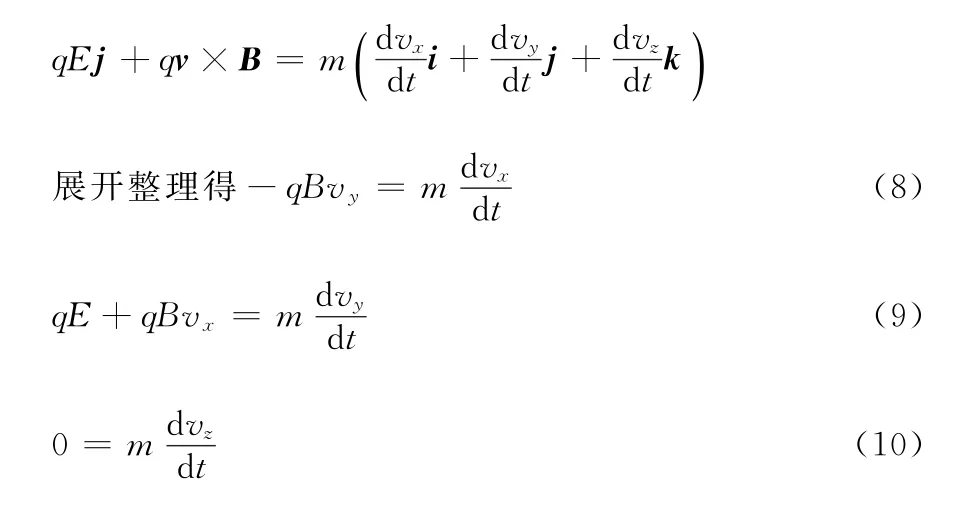
(9)式对时间t求导,并代入(8)式得

说明:

(1)粒子在z轴方向做匀速直线运动,其速度的大小不会对在xOy平面的轨迹有影响;

(2)根据x,y表达式可知,其在xOy平面的轨迹依然为滚轮线。

5.数值模拟图

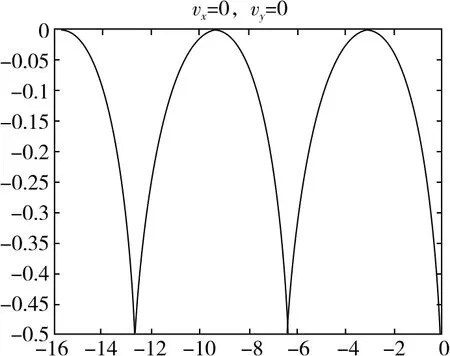
图2

vx0＝vy0＝0,轨迹不会出现越过x轴后交叉现象

图3

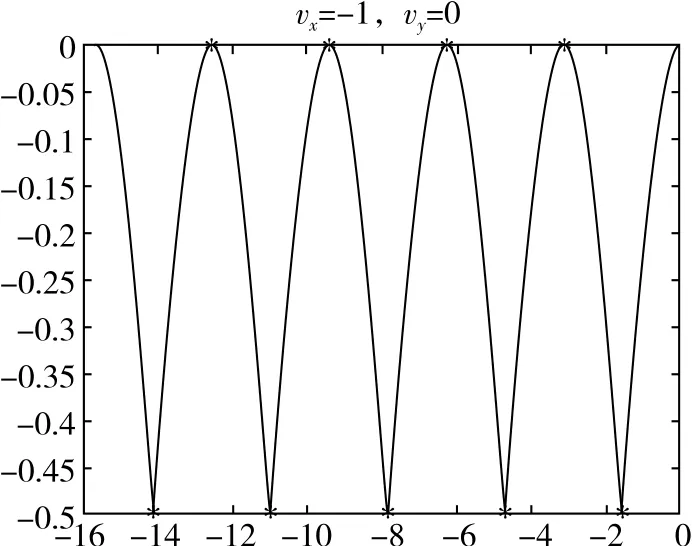
图4

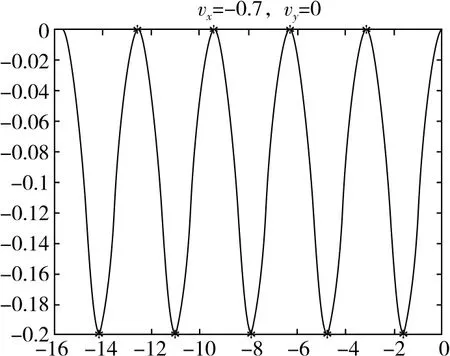
图5

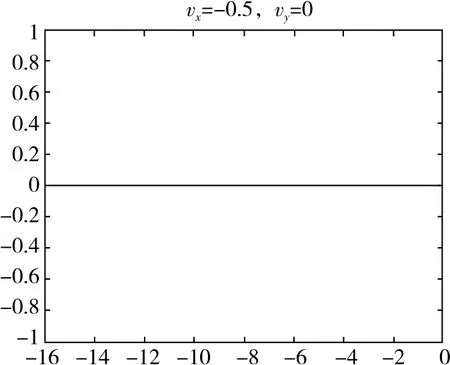
图6

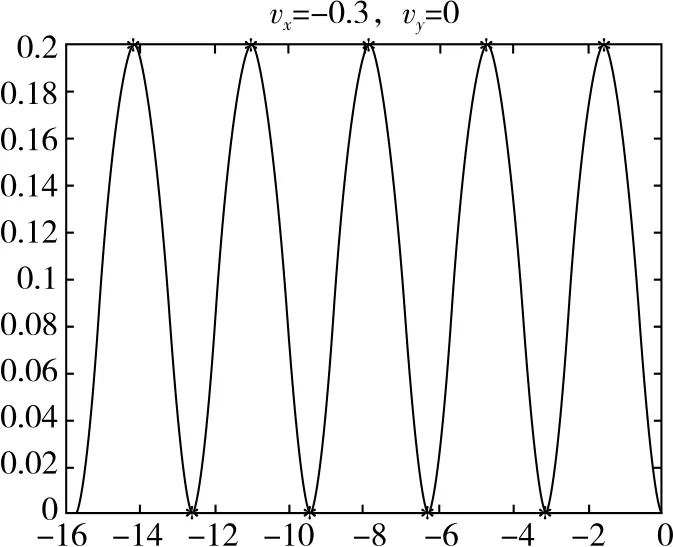
图7

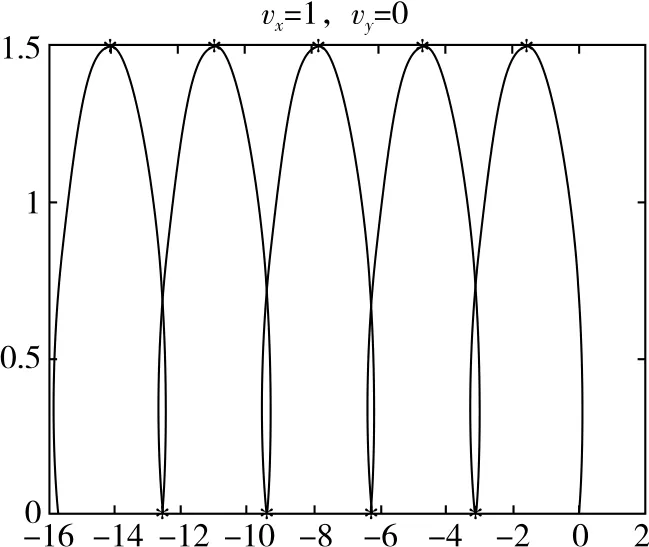
图8

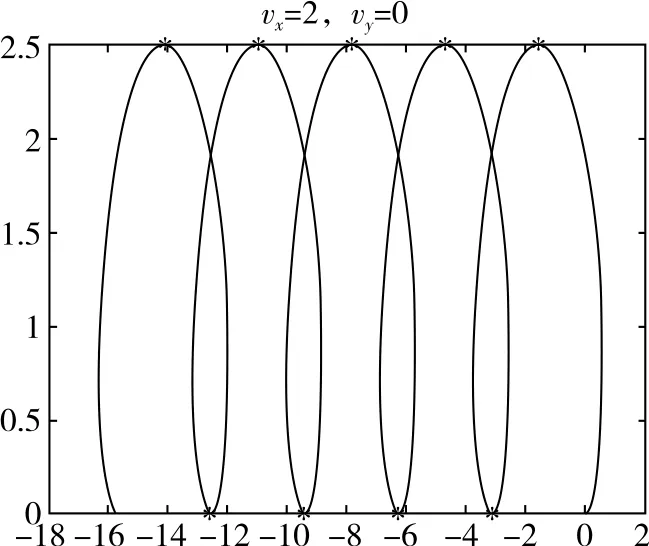
图9

由上述图像可知:

(1)vx0≠0,vy0＝0,当粒子速度较大时会出现交叉现象,速度越大交叉点越高。

(2)vx0∈时,轨迹向下偏转;vx0＝－时,轨迹为一条直线;vx0∈时,轨迹向上偏转。

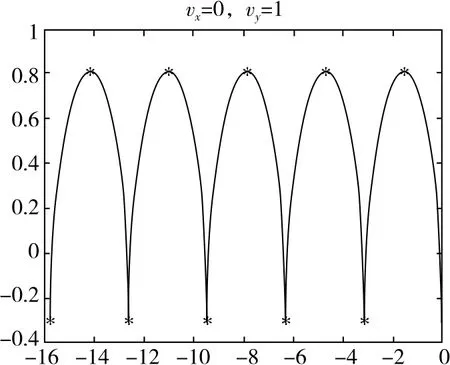
图10

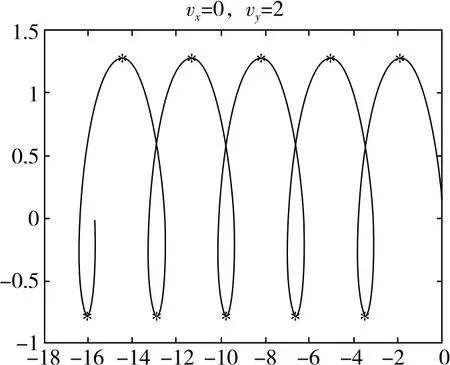
图11

图12

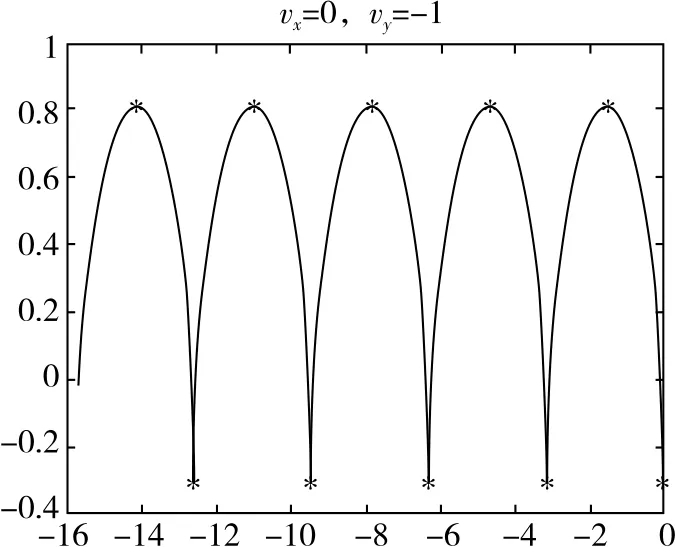
图13

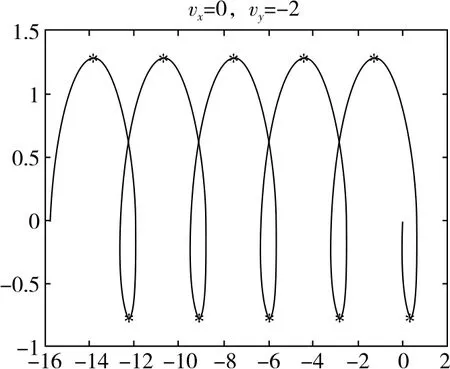
图14

图15

由上述图像可知:

(1)vy0≠0,vx0＝0时,轨迹会穿过x轴;vy0＞0时,轨迹先向上偏转,vy0＜0时,轨迹先向下偏转。

(2)当粒子速度较大时会出现交叉现象,速度越大交叉点越高。

二、小结

综合上述分析,粒子的轨迹与初速度大小、方向均有关系。在高中阶段,采用配速法可以快速有效地厘清粒子的运动情况,通过简单的运动分解,能完美地阐述粒子的运动轨迹,快速地求解相关的物理量。