运动条件螺旋管内流动换热特性研究

朱志明，李可飘，张 魁，田文喜，陈荣华，秋穗正

(西安交通大学 核科学与技术学院，陕西 西安 710049)

近些年来，小型一体化反应堆相关研究受到国内外学者的广泛关注，其具有固有安全性高、空间小、集成化程度高等优点，在海洋核动力系统中具有广阔的应用前景。螺旋管式蒸汽发生器热效率高、布置紧凑，能很好地满足小型反应堆的要求，在小型反应堆设计中得到广泛应用。相较圆管，螺旋管内的二次流效应会给流动传热带来显著影响。当反应堆在海洋中长期运行时，海洋运动对管侧流体作用的运动附加力与原本周期性变化的力叠加，会使管内流场发生复杂的非线性变化[1]。

目前已有很多针对静止条件下螺旋管流动换热特性的试验和理论研究。Naphon等[2]指出螺旋管内局部二次流的搅混作用能够提高螺旋管内的单相流动换热能力。Xiao等[3-8]针对了高压下螺旋管沸腾传热和两相流干涸后传热特性开展了一系列试验研究。Santini等[9]研究得出螺旋管内两相流动的摩擦压降与系统流量的1.19次方呈正比。Wang等[10]通过试验得出螺旋管周向壁温分布不均匀，且不同测温截面的分布规律不同。杨宇鹏等[11]采用数值模拟方法对液态金属螺旋管式蒸汽发生器流动传热特性进行了分析，结果表明螺旋管内过热蒸汽区的热流密度会明显下降。对于海洋条件下的核反应堆系统也有学者开展了相关研究。陈冲[12]对海洋条件下自然循环系统流动换热特性开展了试验和理论研究，结果表明低Re下摇摆运动对自然循环流动换热有促进作用。刘镝[13]基于SIMPLE数值方法，开发了海洋条件自然循环系统及并联通道流动不稳定性分析程序。苏光辉等[14]采用吉尔算法编写了系统分析程序，对运动条件下余热排出系统的除热能力进行了研究，结果表明回路上升过程会加强系统除热能力，下降和倾斜会削弱除热能力。但相关研究尚不充分，海洋条件下螺旋管内流动换热特性几乎是空白，并且运动附加力对管内流体的影响难以直接用程序进行模拟分析。因此，开展海洋条件下自然循环系统螺旋管流动换热特性试验研究，对海洋核动力系统和螺旋管换热器的理论设计，以及相关分析程序的开发具有重要的意义。

本文以海洋条件一体化小堆为原型，搭建海洋运动条件系统自然循环特性试验台架，开展海洋条件回路自然循环流动特性和螺旋管内流动换热特性试验研究，并将螺旋管蒸汽发生器模型和海洋运动模型引入到RELAP5/MOD3.2程序，对试验回路自然循环流动换热特性进行建模计算。

1 试验装置

1.1 试验回路

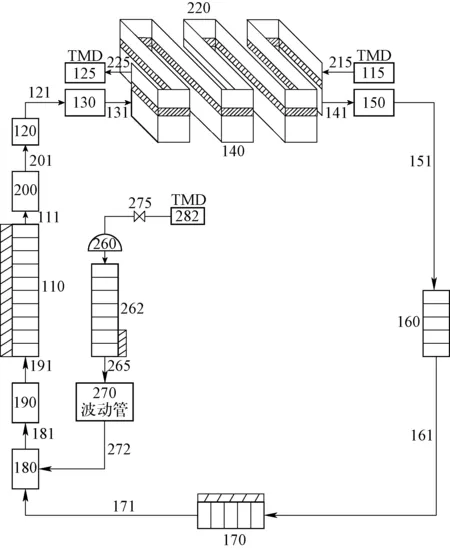
试验装置如图1所示，试验回路主要由主回路、电加热系统、冷却水系统和其他辅助系统组成。主回路主要由试验段、蛇形预热器、套管式冷凝器、稳压器、流量计、加压泵和其他仪器仪表及连接管路等设备组成，采用闭式自然循环运行模式。回路使用加压泵提供初始压力、输入工质以及为稳压器提供液体空间。主回路顶端设置有排气阀，以排出回路中的不凝性气体。工作介质为水，工质经过预热段加热后进入试验段，在试验段内模拟螺旋管式蒸汽发生器二次侧流动换热，之后流经冷凝器被冷却，经过下降段重新回到预热器再次循环。

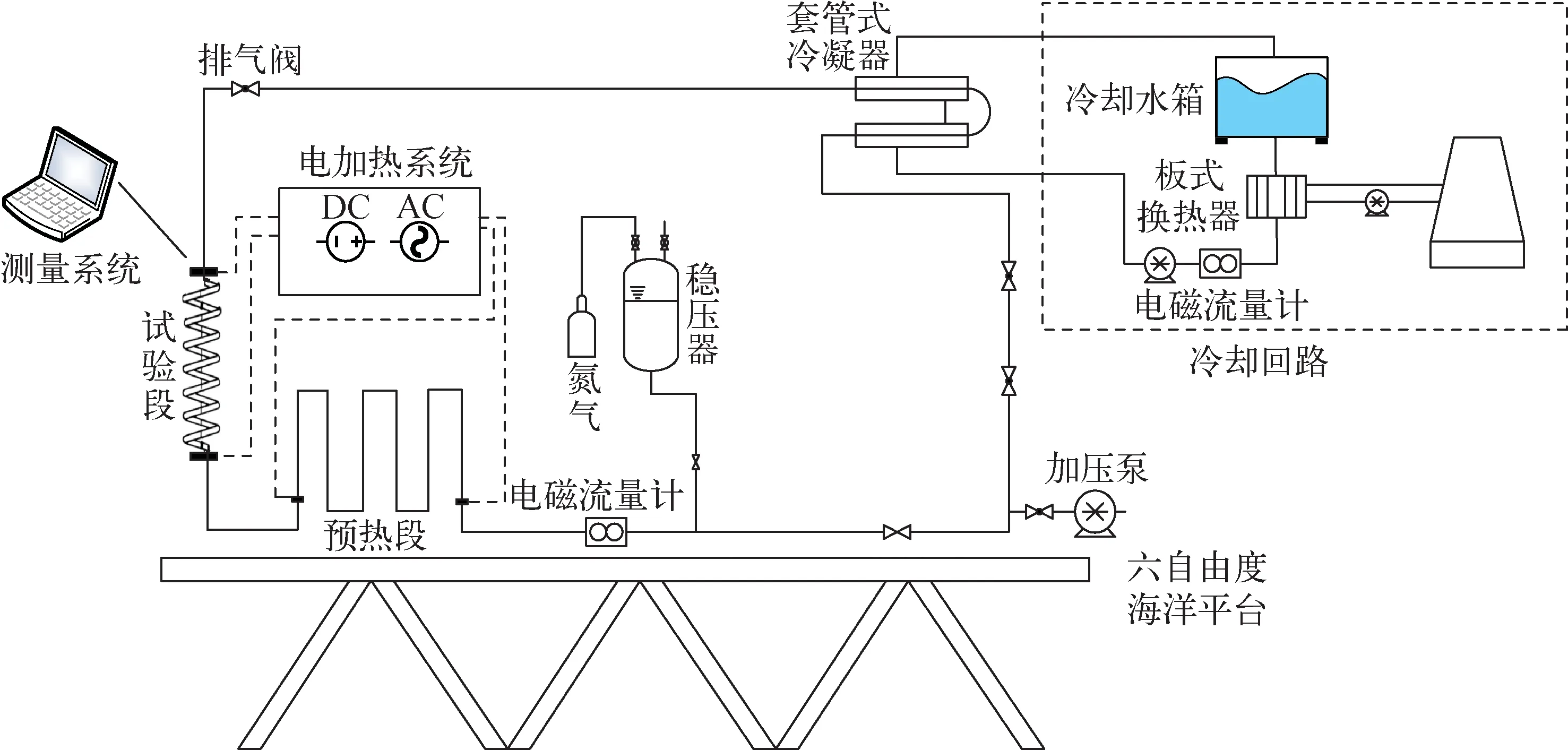
图1 试验装置Fig.1 Experimental apparatus

1.2 运动平台

试验主回路布置在六自由度运动平台上，运动台面为2 m×3 m的矩形台面，可以模拟倾斜、横摇、纵摇、起伏以及耦合运动工况的海洋条件。定义矩形台面中心点O为摇摆运动的中心，台面长边为x轴，短边为y轴，过中心点O且垂直于台面的轴为z轴，绕x轴的运动为横摇，绕y轴的运动为纵摇，沿z轴的运动为起伏。主回路在平台的放置位置如图2所示，回路总高度为3.9 m，试验段距摇摆中心水平距离为0.75 m，加热段中心高度为1.1 m。

图2 回路位置Fig.2 Position of loop

1.3 试验件

试验件采用φ12 mm×1.5 mm的304钢管材弯制而成，包括直管段和螺旋管段两部分，其中直管段长度为0.2 m，螺旋管段总加热长度约为4.65 m，主要尺寸参数列于表1。螺旋管进出口与主回路通过高压法兰进行连接，螺旋管与法兰连接口附近设置了测温组件，用以测量进出口流体温度。螺旋管沿程共设置了8个测温截面，其中第1个测温截面与螺旋管入口距离约为25 cm，第8个测温截面与螺旋管出口距离约为20 cm，各相邻测温截面距离为60 cm。螺旋管采用夹持铜电极的方法进行直流电加热，加热铜排采用三点式布置，其中螺旋管入口和出口处为正极，螺旋管中间为负极。为测量主回路压力及试验段流动压降，在螺旋管段沿流动方向设置5个φ2 mm的引压孔，各取压口等距分布于螺旋管本体，具体位置如图3所示。取压口通过焊接方式与测压绝缘法兰组件连接。

表1 试验段尺寸Table 1 Dimension of test section

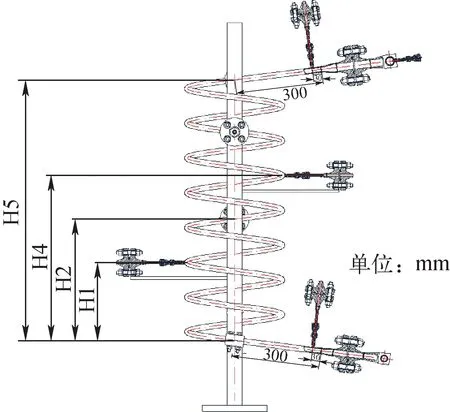
图3 螺旋管试验段设计图Fig.3 Scheme of helical-coiled tube test section

自然循环过程中，管内流体除了受浮升力及流动阻力影响，还受到离心力影响，因此沿螺旋管周向的壁温和流体换热特性差别较为明显，为研究螺旋管内流体换热能力沿周向分布的不均匀性，在每个测温截面周向布置了8个热电偶进行测量(图4)。

图4 壁温测点布置Fig.4 Arrangement of point for measuring wall temperature

2 结果与讨论

2.1 单相流动阻力特性

1) 倾斜运动条件

为了探究回路从水平静止到倾斜状态过程中两种稳态状况的转变过程，本研究中倾斜工况共分为5个阶段：t=0 s时开始数据记录，回路处于水平静止稳态；记录10 s后启动运动平台开始倾斜运动；经过约70～75 s后达到预定的倾斜位置；等待回路参数稳定后，t=300 s时启动运动平台，回路由倾斜恢复水平，时间约为30～40 s；在水平状态下等待回路参数重新稳定后停止数据记录。

倾斜运动过程试验回路流量变化如图5所示。图中：RX代表横倾；RY代表纵倾，下同。其中，单倾斜为仅有绕x轴或y轴1个自由度的倾斜状态，耦合倾斜为两自由度的倾斜状态。当回路开始倾斜后，由于运动附加力作用，回路流量先短暂增加，随后持续下降，在达到固定的倾斜角度后，回路流量经过小幅增加后达到稳态值；回路由倾斜开始恢复水平时，流量先随运动而增加，在刚回到水平位置时流量达到最大值，随后流量开始减小，达到最小流量后回升至稳态流量。倾斜会使回路自然循环流量降低，且降低幅度随着倾斜角度的增加而增大。倾斜状态下回路稳态流量减小的主要原因是回路冷热源间高度差降低，导致自然循环驱动力减小。由于回路相对位置原因，横倾工况下回路冷热源间高度差变化值小于纵倾条件下的，对自然循环驱动力影响较小，因此相同倾斜角度下横倾对自然循环流量的影响小于纵倾的。

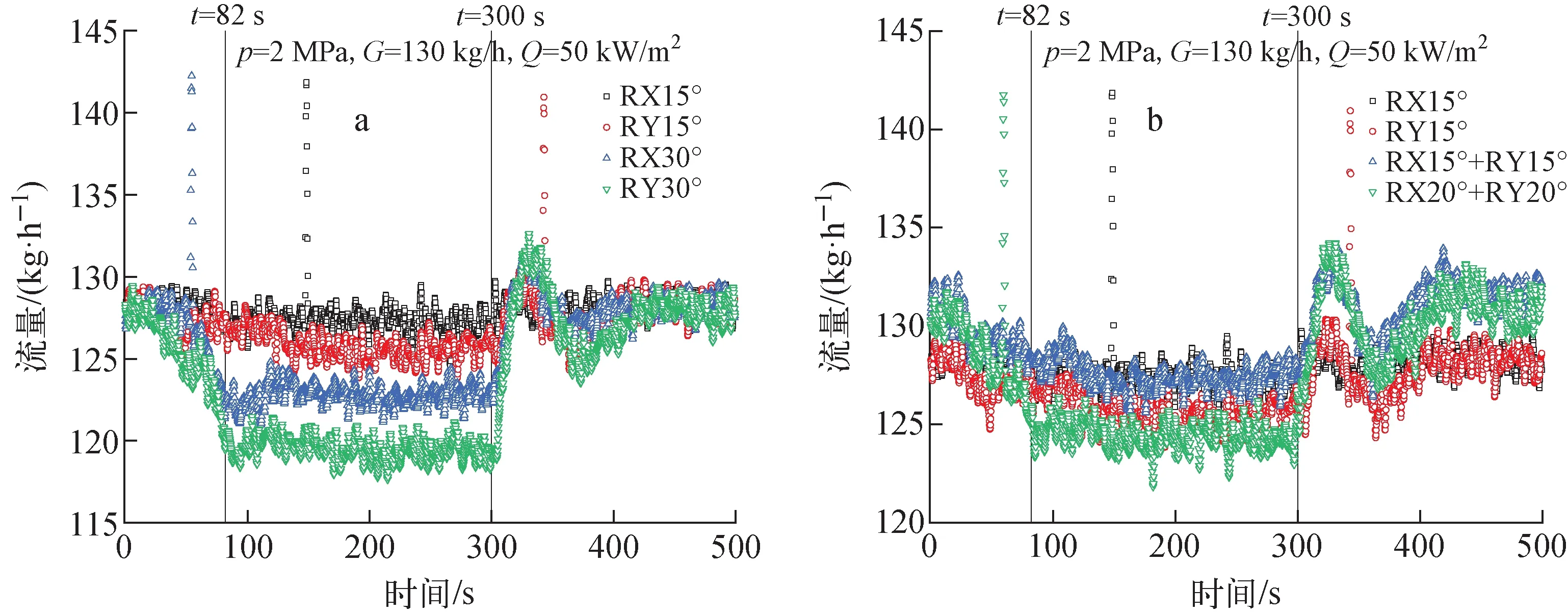
a——单倾斜工况流量；b——单倾斜与耦合倾斜流量对比图5 倾斜工况回路流量变化Fig.5 Variation of flow rate under tilting motion

图6为倾斜工况下试验段进出口压降波动情况，可以看出，纵倾对试验段压降的影响程度明显大于横倾。相同倾斜角度的横倾、纵倾复合工况下，压降变化主要受纵倾运动影响。不同倾斜工况试验段摩擦阻力系数变化的趋势与压降变化趋势一致(图7)，但倾斜稳态阻力系数相比水平状态减小幅度远小于压降。由于在倾斜条件下，稳态压降与流量均小于水平状态，且自然循环流量相比稳态的降低幅度更大，因此倾斜状态下稳态阻力系数相比水平略微降低。

a——单倾斜工况；b——单倾斜与耦合倾斜对比图6 倾斜工况试验段压降变化Fig.6 Variation of pressure drop in test section under tilting motion

a——单倾斜工况；b——单倾斜与耦合倾斜对比图7 倾斜工况试验段摩擦阻力系数Fig.7 Friction drag coefficient of test section under tilting motion

2) 横摇运动条件

定义瞬时压降与时均压降的比值为相对压降，图8为不同摇摆工况下相对压降变化。图中，X5T6表示横摇5°、周期6 s，余同。由图8可看出，相对摩擦压降随时间呈周期变化，相对摩擦压降的波动幅度随着横摇角度的增加和摇摆周期的减小而增大，并且剧烈的摇摆运动可能会导致试验段内工质产生短暂的倒流现象。另外，角加速度对压降的波动影响相较于最大角速度更为明显。

a——角度影响；b——周期影响图8 不同摇摆工况下相对压降变化Fig.8 Variation of normalized pressure drop under different rolling conditions

图9为不同Re下试验段摩擦压降和相对摩擦压降的变化，可看出，相同运动条件下试验段摩擦压降波动的绝对值随着平均Re的增加而增加，但相对值随着平均Re的增加而减小，这说明在高Re工况下，摩擦压降的相对波动幅度不仅与摇摆速度相关，而且试验段平均Re越高，摇摆运动对回路流动阻力的影响相对越弱。

图9 不同Re和摇摆条件下压降变化Fig.9 Variation of pressure drop under rolling conditions at different Re

3) 纵摇运动条件

纵摇运动下回路流量和试验段压降呈现周期变化(图10，图中，Y15T6表示纵摇15°、周期6 s)，但波动幅度远小于横摇运动。摇摆条件下，试验段压降的波动主要取决于两方面因素：首先，摇摆运动引起回路流量波动，进而使摩擦阻力产生变化；其次，运动横向附加力会加强流体对管壁的冲刷，使管内湍流更加剧烈，导致流动阻力系数和摩擦压降增加。在横摇运动下，回路流量波动幅度较大，对摩擦阻力系数起主要影响，而纵摇运动下，流量波动小，因此横向附加力引起的冲刷作用对摩擦阻力起更重要的作用。

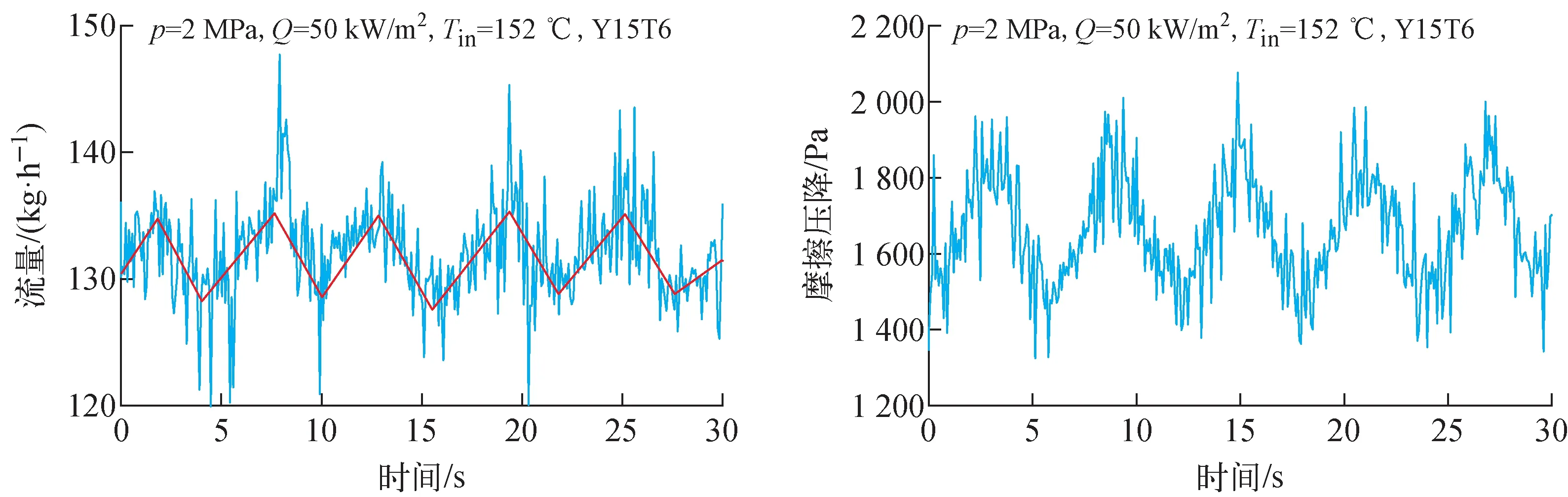
图10 纵摇运动下流量与压降波动Fig.10 Variations of flow rate and pressure drop under longitudinal rolling motion

4) 起伏运动条件

图11为运动幅值100 mm、周期分别为1 s和3 s的两种起伏工况下回路压降和流量波动情况。图中，Z表示起伏。可看出，只有周期1 s工况下，试验段摩擦压降随起伏呈现出了周期波动。起伏运动对自然循环流动的影响主要来自于起伏运动产生的竖直方向附加力与回路中流体本身受到的重力叠加作用，在本研究中受平台负载能力限制，在起伏运动加速度较小时产生的附加力相对于重力几乎可忽略，而起伏距离100 mm、周期1 s的工况下，加速度约为0.16g，此时起伏运动加速度所产生的附加力才足够影响回路的循环能力。

图11 起伏运动下流量和压降变化Fig.11 Variations of flow rate and pressure drop under undulating motion

5) 耦合运动条件

图12为横摇以及包含横摇的耦合运动下回路流量及试验段摩擦压降变化对比。从图12可看出，单横摇运动与耦合运动引起的回路流量和压降变化几乎完全相同，相对于横摇运动，纵摇和起伏对回路参数的影响较小。因此对相同周期和摇摆角度的横摇与纵摇或起伏耦合运动，可直接简化为横摇运动进行处理。

图12 横摇与耦合运动工况参数变化Fig.12 Variation of parameters under rolling and coupling motions

2.2 单相流动换热特性

1) 倾斜运动条件

不同倾斜条件对入口温度的影响如图13所示，螺旋管入口温度的最高值约出现在达到倾斜角度后20～30 s，瞬态温度最低值约出现在平台刚恢复水平位置时，且纵倾工况下温度波动的幅值以及倾斜状态下流体温度稳态值均高于同等角度下的横倾工况。倾斜工况中初始状态、入口温度最高点、倾斜稳态值以及入口温度最低点的试验段热效率如图14所示。从图14可看出，倾斜工况下稳态热效率均低于静止条件，且倾斜角度越大，稳态热效率降低越多，这是由于回路倾斜导致流量减小，因此试验段换热能力越弱。同等倾斜角度下，横倾的热效率降幅最小，横倾与纵倾耦合工况的热效率降幅最大。

图13 倾斜运动对试验段入口温度影响Fig.13 Influence of tilting motion on inlet temperature of test section

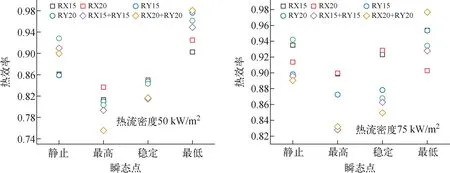
图14 倾斜工况部分瞬态热效率Fig.14 Partial transient thermal efficiency under tilting motion

2) 摇摆运动条件

图15为两组热工工况静止状态下不同截面的壁温分布。可看出，同一截面周向壁温分布不均匀，距离螺旋管轴线较近的测点壁温更高。这是由于螺旋管内流体受到与流动方向垂直、指向旋转轴线反方向的离心力作用，因此远离轴线方向的流体与管壁对流换热得到了强化，距离轴线较远的外侧区域的局部对流换热系数高于内侧区域。

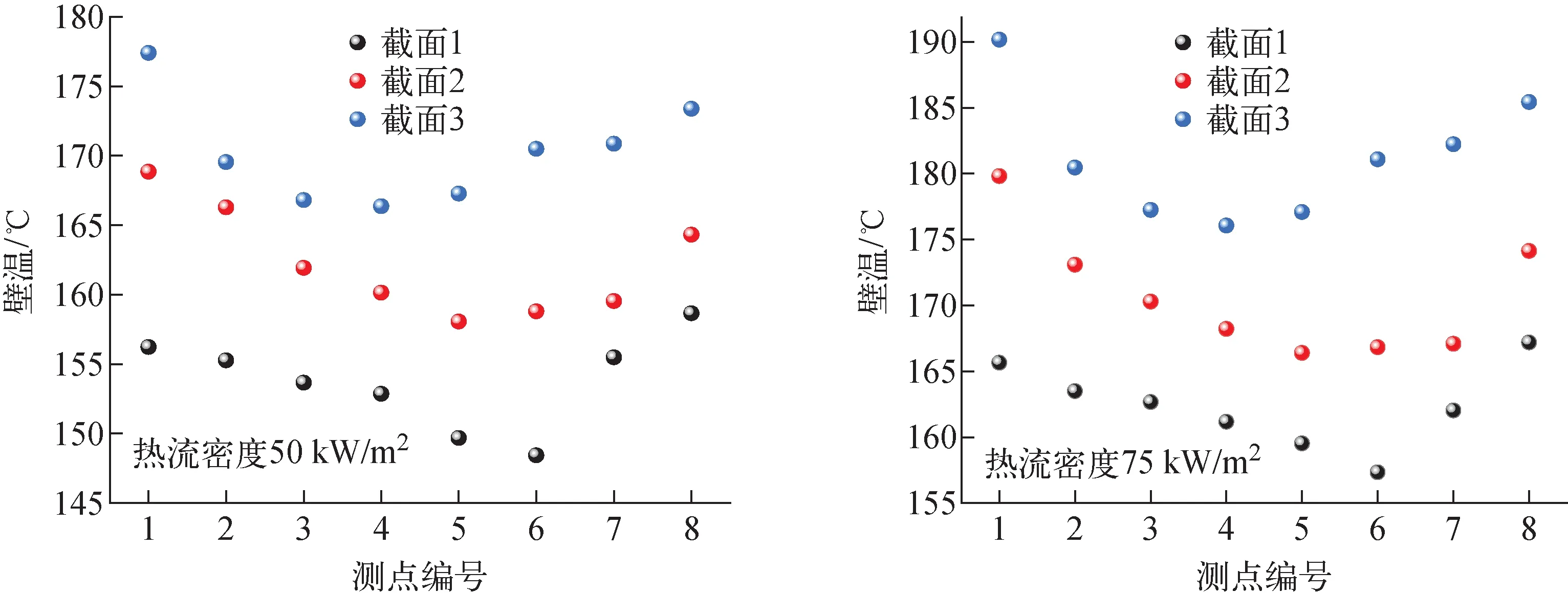
图15 静止状态下壁温分布Fig.15 Wall temperature distribution under stationary condition

摇摆运动对螺旋管壁温周期平均值的影响如图16所示。摇摆条件下壁温分布特性与静止条件下一致，壁温的波动幅值仅取决于运动条件。运动条件下同一测点的壁温高于静止条件；摇摆方向相同时，壁温上升值随着摇摆角度的增大和周期减小而增加，单横摇运动壁温上升幅度大于纵摇。摇摆运动附加力对壁温周向分布的影响较小，流体因螺旋管结构特性而受到的离心力对壁温周向不均匀特性仍起主导作用。

不同摇摆条件下，同一测温截面平均局部换热系数h如图17所示，螺旋管同一截面的周向局部换热系数差别很大，海洋条件下壁温波动会导致局部换热系数变化。将螺旋管周向分为两个不同的区域(图18)，分别是内侧区域，即壁温测点编号7-8-1-2-3的半圆形区域，以及外侧区域，即壁温测点3-4-5-6-7的半圆形。其中内侧区域壁温较高，局部换热系数低，而外侧为壁温较低的区域，局部换热系数远高于内侧区域，摇摆条件引起的壁温波动对换热系数的影响也远大于内侧区域，即海洋条件对螺旋管换热能力的影响，主要体现在外侧区域。

图17 摇摆条件螺旋管周向局部换热系数Fig.17 Circumferential local heat transfer coefficient of helical-coiled tube under rocking condition

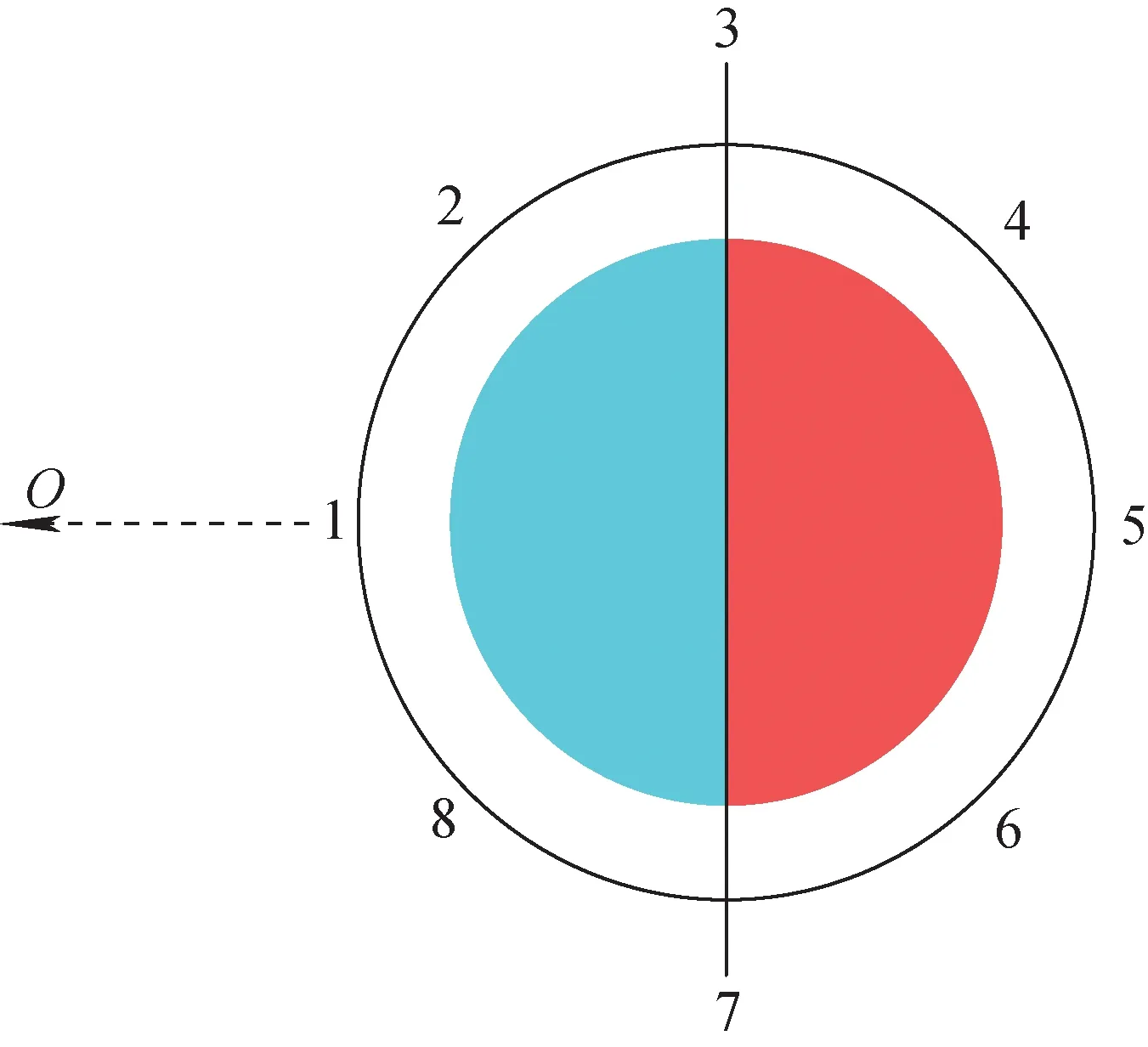
图18 螺旋管换热系数分布Fig.18 Distribution of heat transfer coefficient in helical-coiled tube

摇摆运动对螺旋管周期平均Nu的影响如图19所示，可看出，低Re工况下摇摆运动对螺旋管换热特性影响明显，当Re>32 500时，纵摇对螺旋管平均Nu的影响几乎可忽略不计，Re>35 000时，横摇运动对平均Nu的影响也可忽略不计。本研究中横摇运动下螺旋管平均换热能力低于静止状态，纵摇运动下螺旋管平均换热能力高于静止状态，且横摇、纵摇对螺旋管换热能力的影响随着运动幅值和加速度的增加而增加，随着Re的增加而降低。

图19 摇摆条件螺旋管NuFig.19 Nu of helical-coiled tube under rolling condition

3) 起伏运动条件

起伏工况下螺旋管平均壁温与静止条件下几乎无差别，流体入口温度和出口温度未随运动呈现周期性变化(图20)。说明在本研究中起伏运动对螺旋管试验段的换热特性无明显影响。

图20 起伏运动对螺旋管壁温和流体温度的影响Fig.20 Influence of undulating motion on temperatures of helical-coiled tube wall and fluid

4) 耦合运动条件

耦合运动条件下Nu的变化规律与对应的单横摇运动基本一致(图21)，这是由本研究试验回路布置及回路在运动平台上的摆放位置决定的。当回路做横摇运动时，试验回路的四条边均垂直于摇摆轴，纵摇运动时水平部分平行于摇摆轴，此时水平部分流体受到的运动附加力垂直于流动方向，对于流体流动换热的影响几乎可忽略，因此在横摇运动下流体受到的沿流动方向的附加力的分力更为显著，所以横摇对系统参数波动幅度以及流动换热能力的影响都明显高于纵摇。

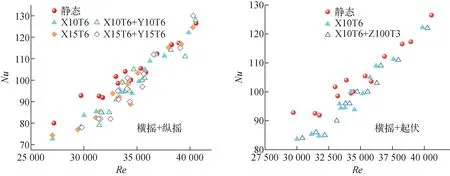
图21 耦合与单一海洋运动螺旋管Nu对比Fig.21 Comparison of Nu of helical-coiled tube under single and coupled motions

5) 流动换热经验关系式

静止状态下，螺旋管Nu试验值与D-B公式以及Hardik提出的螺旋管流动换热关系式对比如图22所示。一般以D-B公式来衡量圆管湍流区域的换热能力，本试验工况范围内，随着Re的增加，截面换热系数相较圆管明显提高，最大约高过15%。这是由于表征螺旋管弯管效应的参数为迪恩数De=Re(d/Dc)0.5，迪恩数随着Re单调递增，因此在高Re情况下，螺旋管结构引起的管内二次流效应更为显著，促进了管内流体的流动搅混，从而增强了螺旋管换热能力。

图22 Nu试验值与经验关系式对比Fig.22 Comparison of experimental values and empirical relations for Nu

基于试验数据，以D-B公式为基本形式，总结得到了本试验螺旋管静止状态下的Nu半经验关系式：

Nu=0.043 5(Dc/di)-0.16Re0.8Pr0.3

(1)

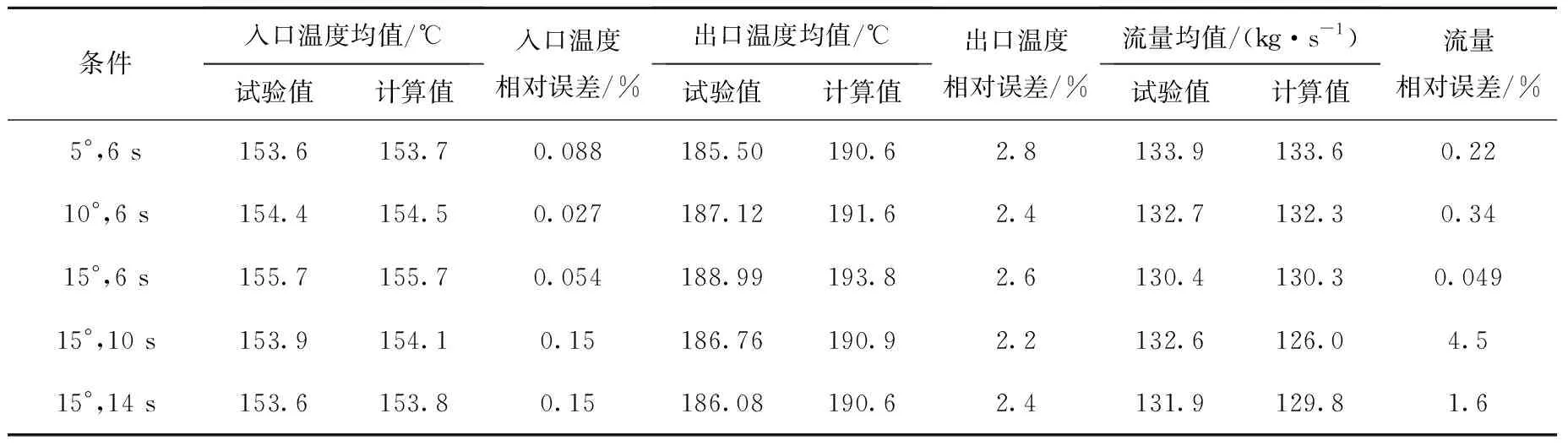
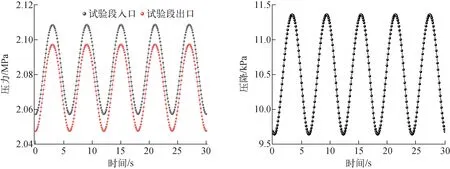
式中：Dc为螺旋直径；di为管内径；Pr为普朗特数；适用范围为25 000

本试验中，根据海洋条件试验值，对式(1)进行海洋条件修正：

Nu=(1+C)0.043 5(Dc/di)-0.16Re0.8Pr0.3

(2)

2.3 自然循环系统流动不稳定性

本研究对回路在2 MPa压力，低含气率下的自然循环发生条件进行了研究。在静止状态下提高试验段加热功率，直到发生系统流动不稳定性后，略微降低功率，使回路退回稳定状态，开启海洋平台，逐渐增大运动参数，观察是否出现流动不稳定性现象以及流动不稳定性的剧烈程度，来判断不同的运动条件对系统流动不稳定性发生点的影响。

经过试验发现，在本研究的运动工况范围内，横摇、纵摇以及起伏运动均不会使回路自然循环流动不稳定性提前出现，倾斜会使流动不稳定性提前发生，且纵倾运动对流动不稳定性的影响大于横倾。

图23为系统参数变化。从图23可看出，回路倾斜会导致流动不稳定性提前发生，且倾斜角度越大，回路参数波动越剧烈，流动不稳定性现象更加显著，同等倾斜角度下，纵倾引起的不稳定性波动大于横倾。当回路发生此类流动不稳定性时，流体出口温度波动幅度大于入口温度，且靠近试验段入口、温度较低的壁面温度波动幅度大于温度较高的壁面，与运动条件附加力引起的回路流动换热参数波动趋势不相符，温度较低的区域壁温和流体温度的平均值与静止条件下温度差别较小，而温度较高的区域流体温度与壁温均低于静止状态下的值。回路平均流量与静止条件下差别较小，因此此时回路时均换热效率较静止条件下更低，且试验段出口附近流动换热能力受影响更加严重。此状态下，回路周期平均流动压降远高于水平位置，由于平均流量变化较小，因此流动不稳定性发生时，回路平均流动阻力损失大幅增加。

图23 系统参数变化Fig.23 Variation of parameter

3 试验模拟计算

3.1 回路建模

采用基于RELAP5 Mod3.2程序进行二次开发后的系统程序[15-16]针对试验回路中的主要部件建立节点图模型，如图24所示。回路主要部件包含螺旋管试验段、冷凝器、预热器以及稳压器。

图24 试验回路的RELAP5节点图Fig.24 RELAP5 model of test loop

3.2 静止条件

静止条件的计算值与对应工况的试验值对列于表2。由结果可看出，主要热工水力参数的计算值与稳态值吻合较好，可验证所建立模型准确可靠。

表2 静止条件计算结果Table 2 Calculation result under stationary condition

3.3 运动条件

图25、26分别为横摇运动10°、6 s和15°、6 s以及横摇与纵摇叠加的复合运动的回路流量试验值与RELAP5计算值对比。可看出，程序计算的自然循环流量同样呈现出周期性波动，周期与摇摆周期一致，流量波动范围与试验值有微小差别，误差在3%以内。

图25 横摇运动流量变化Fig.25 Variation of flow rate under rolling motion condition

图26 复合运动流量变化Fig.26 Variation of flow rate under coupled motion condition

表3列出RELAP5计算得到的横摇运动下部分参数的结果与试验值的对比，可看出计算值与试验值的相对误差都在5%以内，试验值与计算值符合较好。

表3 横摇运动计算结果Table 3 Calculation result under rolling motion condition

图27为计算得到的摇摆过程中试验段进出口压力变化以及进出口压降。从图27可看出，试验段进出口压力和压降均呈现出周期性波动，波动周期与摇摆周期一致，与试验所得规律相符。

图27 压降变化Fig.27 Variation of pressure drop

由以上计算结果分析可看出，通过对本研究中的试验回路进行RELAP5建模，并进行海洋条件瞬态分析，得到的计算值与试验值的误差均在可接受范围内，计算值与试验值吻合程度较高，因此可知采用此瞬态分析程序对海洋条件下反应堆建模计算可行。

4 结论

本文典型海洋运动条件下系统自然循环特性和螺旋管内换热特性开展了试验研究和程序建模分析，得到的主要结论如下。

1) 倾斜运动会使回路稳态流量和流动压降下降。摇摆条件下，平均阻力系数较静止条件略有提高。

2) 倾斜条件下稳态热效率低于水平状态，横倾与纵倾耦合会进一步降低热效率。海洋运动条件对螺旋管对外侧区域传热系数影响剧烈。摇摆运动对平均Nu的影响随试验段平均Re的增加而减小，起伏对回路流动换热参数几乎无影响。基于试验数据和文献总结了海洋运动条件下螺旋管内换热经验关系式。

3) 试验条件下摇摆运动不会改变自然循环流动不稳定性边界，倾斜运动会降低流动不稳定性阈值，随着倾斜角度的增加，流动不稳定性程度也更剧烈。

4) 二次开发的RELAP5能较准确地对摇摆条件下试验回路流动换热特性进行计算分析，对短周期、大幅值的横摇工况模拟结果表明，剧烈的横摇会进一步削弱回路自然循环能力和螺旋管换热能力。