高陡边坡岩体结构信息无人机识别与离散元数值模拟*

沙 鹏 孔德珩 王绍亮 伍法权

(①绍兴文理学院，浙江省岩石力学与地质灾害重点实验室，绍兴 312000，中国)(②同济大学，土木工程学院，上海 200092，中国)(③浙江省工程勘察设计院集团有限公司，宁波 315012，中国)

0 引 言

岩质高陡边坡的稳定性评价需要地质工作者在现场调查、测量、分析的基础上，明确边坡岩体结构的空间展布状态(孙广忠，1993；黄润秋等，2004)。对于复杂艰险山区的自然高边坡，测量人员根本无法到达所需要测量的区域，传统测量方法无法满足大断面岩体结构测量(于天亮，2009)。对于水电、矿山等工程开挖形成的高陡边坡，现场要求快速完成地质编录工作，不仅需要投入大量人力，而且崩塌等偶发情况可能对测量人员带来安全隐患。因此，岩体工程领域需要引进快速、高精度、高效率且对地形地貌有较好适应性的调查技术。

随着三维空间影像技术的不断成熟与完善，如数字近景摄影测量(王凤艳等，2008)、无人机低空遥感技术(Giordan et al.，2018；张恺等，2019)和三维激光扫描技术(Jaboyedoff et al.，2012；Riquelme et al.，2015；梁玉飞等，2021)等，为解决上述问题提供了新的思路。其中：无人机低空遥感技术和三维激光扫描技术能够远距离、高精度快速获取点云数据，便于进行三维重建和算法智能解译，这为实现结构面的精细化识别和参数提取提供了技术支持(Feng et al.，2014；Chen et al.，2016)。基于三维点云模型识别岩体结构面的研究日益增多。基于不规则三角网模型以及不同的几何特征聚类分析，如模糊K-均值算法与改进K-均值算法等实现结构面产状与分组的自动识别(Slob，2010；Vöge et al.，2013；Liu L et al.，2019)。Kong et al.(2020)利用通过快速搜索和查找密度峰(CFSFDP)算法进行聚类来自动检测聚类的数量，提高了准确性并缩短计算时间。结构面的间距和线密度可通过虚拟精测线法、平面间距离计算等方法在三维点云数据中提取(葛云峰等，2017)。可以看出，大部分前人研究主要以某个结构参数，如产状、间距等参数的识别方法为主，尚未完整建立岩体结构模型。

另一方面，如何建立精确的数值计算模型开展数值模拟也是边坡稳定性分析中的研究热点。不少学者通过致力于进行三维地学建模与数值模拟的耦合，弥补数值模型在建立复杂三维地质模型上的不便(崔芳鹏等，2008；徐文杰等，2008)。三维点云数据可以获取边坡地形与关键块体信息，通过相关软件将DEM导入数值模拟软件，分析不同工况下的边坡形变或不稳定块体运动，实现边坡稳定性评价的目的(Havaej et al.，2016；Liu C et al.，2019；金爱兵等，2021)，但上述研究成果尚未考虑结构面对岩质边坡稳定性的影响。如何利用三维点云数据建立岩体结构模型，结合DEM快速建立三维离散元数值分析模型需要进一步开展研究。基于此，本文结合露天矿山高边坡无人机地质调查，基于获取的三维点云数据实现岩体结构几何信息的自动识别。采用曲面重构和“Rhino-Griddle-3DEC”联合建模方法，建立边坡三维离散元数值模型。结合岩体结构统计模型，构建离散裂隙网络(DFN)切割边坡模型，开展边坡稳定性分析计算。

1 工程背景

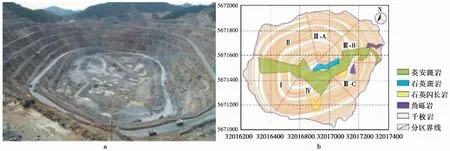
图1 银山铜矿露天边坡全景与岩体分区Fig.1 Panorama of Yinshan copper open pit slope and distribution of rock massesa.高陡岩质边坡；b.各分区岩体分布

边坡岩体主要为千枚岩，其次有安斑岩、石英斑岩、石英闪长岩等，具体岩体分布特征如图1b。其中：I区-Ⅱ区的岩体主要为绢云母千枚岩，片理发育程度不高，构造裂隙不甚发育。Ⅲ区千枚岩片理发育，岩体较破碎，构造裂隙较发育，且根据英安斑岩、石英斑岩等分布情况继续划分成A、B、C 3部分。Ⅳ区内千枚岩发育一组片理，主要产状为285°∠82°。

表 1 大疆Phantom 4 Pro 四旋翼无人机主要参数Table1 Main parameters of DJI Phantom 4 Pro UAV system

2 无人机点云数据处理

2.1 测试方案

图2 矿山边坡无人机测量Fig.2 UAV measurements of the open pit slope

2.2 无人机点云数据获取及处理

采用运动恢复结构法(Structure-from-Motion，SfM)，筛选无人机航拍图像导入Context Capture软件，生成矿山边坡各个分区的高精度三维点云模型，如图3所示。SfM法是通过图像集中的同名点来估计静止场景中运动相机的相对参数，使用相机参数以及同名点间对极几何关系来获取三维点云模型，恢复三维场景的一种方法(Westoby et al.，2012)。这个过程涉及三维几何和摄像机运动姿态的同时估计运算，因此称为运动恢复结构(孙钰杰，2016)。

图3 露天矿山边坡各区无人机点云图像Fig.3 UAV photogrammetry of districts of open-pit slope

由于分区较多，受篇幅限制下文只针对北东边坡Ⅲ-B区域进行详细分析。在Ⅲ-B区域(东处高边坡120m平台)共设地面控制标靶站点4处，获得航片872张。为了获得精确的位置，测量数据需要利用机载镜头的投影矩阵来计算出匹配点的三维坐标。此方法流程图如图4所示，包括数据预处理、特征点提取匹配、稀疏重构、密集重构。

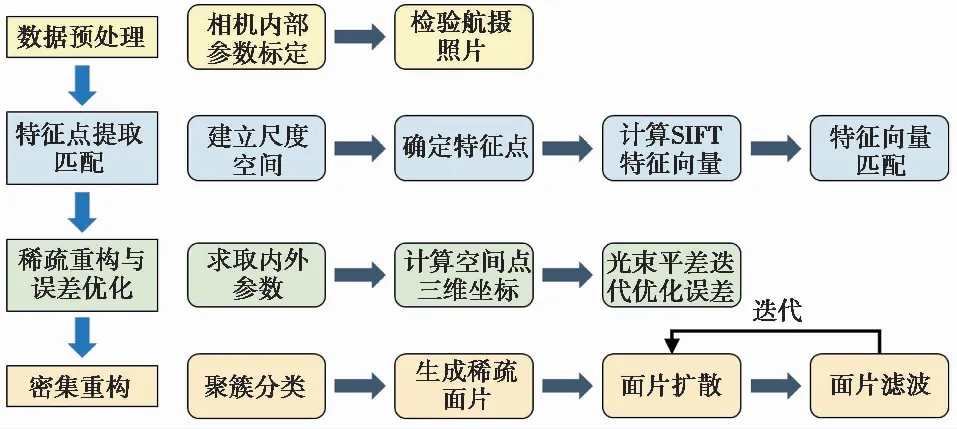
图4 SfM技术流程图Fig.4 The flow chart of SfM method

(1)数据预处理：完成相机的内部参数标定和检验拍摄照片的质量。

(2)特征点提取匹配：特征点匹配是寻找不同影像中相同特征点的过程。考虑到使用无人机进行拍摄，会出现照片尺度、旋转角度、环境光强度、模糊程度的变化，因此采用尺度不变特征变换算法(SIFT，Lowe，2004)对航摄图像进行特征提取匹配。该算法提取特征点时具有图像旋转、平移、缩放以及仿射不变型和一定的抗光照强度及视角变化能力，具体操作步骤为：

1)使用高斯卷积函数对无人机航拍图像进行尺度变换，获得图像在不同尺度下的表达序列。

2)利用尺度空间高斯差分的方程形式对图像进行卷积求取极值，这些极值所对应的极值点即是图像的特征点。

3)将坐标轴旋转到特征点方向，以保证旋转角度不变，然后计算SIFT特征向量。

4)结合无人机采集图像时的RTK-GPS坐标信息、惯性测量单元位姿角度信息建立图像间的拓扑结构，利用最邻近算法计算出图像间特征点的对应关系完成匹配工作。

(3)稀疏重构：利用上述匹配出具有同名特征的点集对测量场景进行增量式重构，得到初步的三维点云模型。基本流程是：

1)首先求取内外参数，整个测量过程中，无人机通过同一镜头拍摄，因此图像的内部参数是固定的，只需计算获得图像的外部参数即图像间的旋转矩阵和平移向量。

2)根据相邻图片的内外参数，采用三角定位方法解算空间点的三维坐标。

3)由于特征点匹配并不是绝对精确，因此步骤②中求得三维点坐标存在误差。采用光束平差法，通过逐步迭代最小化投影点和观测图像点之间的重投影误差，可以得到机载镜头最佳姿态和所测场景的三维点云坐标。

4)密集重构：由于稀疏重构所恢复的三维点云模型无法对岩体这类不规则物体进行精细描述。因此，需要对点云模型进行密集重构，即增加点云密度提高模型的精细程度。采用Furukawa et al.(2010)提出的稠密重建算法(CMVS-PMVS)，采用聚簇分类去除原始图像组中的冗余图像；选取可信度较高的稀疏匹配点生成一系列稀疏面片；将对应的图像区域进行反复的扩散、滤波，最终得到更为精细的密集点云数据。

如图5所示，通过上述4步处理，Ⅲ-B区120m平台共生成点云数量64，353，602个，构建了长度约20m，高度约12m的三维点云模型。截取长18m、高6m且结构面出露较好的矩形区域，利用点云数据包含的真实空间坐标信息开展后续的结构面的智能识别和几何信息解译。基本思路主要是通过算法自动处理整体点云数据，筛选出代表结构面的点，实现程序化识别结构面。

图5 Ⅲ-B区部分航拍照片(a)；Ⅲ-B区局部点云(b)Fig.5 Partial aerial photos of area Ⅲ-B(a)；Partial point cloud of Ⅲ-B area(b)

3 结构面自动提取方法

3.1 点法向量计算

本文采用基于Riquelme et al.(2014)提出的迭代加权平面拟合(IRPF)方法，计算区域露头点云集合内的各点法向量。具体可分为以下3个部分：

(1)估算每个点的初始法向量。利用式(1)进行迭代的加权平面拟合，其中将σd设置为局部点间距δl，将σr设置为最大拟合残差的1/3，每个点的初始拟合剩余权重设置为1。当涉及的权重稳定或迭代次数超过所设限制的20时，迭代即终止。

(1)

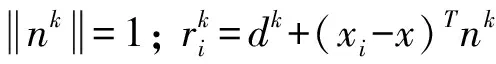
(2)

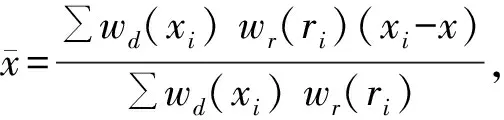
(2)估算局部自适应带宽。对于任意点，将其邻近点的法向量在3δl之间的距离内进行聚类，以便自动确定其特征系数。生成尖锐的特征点百分比曲线时，角度阈值从0开始，以2.5°为增量增加。找到合适的阈值并估计每个点的特征系数后，根据式(3)和式(4)设置3个权重带宽。

(3)

(4)

因此，对于平滑区域中的点(Fcoe=0)，距离带宽为δl。对于尖锐特征点(Fcoe=1)，距离带宽2δl将包含更多邻近点，以补偿由于剩余和正常差值权重而丢弃的邻近点的缺失。

(3)改善初始法向量。采用式(5)来改善初始法向量，迭代计算通过与式(1)中相同的方式终止。

(5)

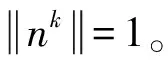
3.2 识别同组结构面并聚类分割

根据求得的各点法向量对点云数据进行相似性判断和聚类，确定主要点云集合即为同组结构面，并在赤平投影图中进行统计分析，由此得到点云集合的主要方向即该组结构面的优势产状，整个过程采用基于划分的K-Means算法(Macqueen，1967)。通过对点云集合进行聚类分割与平面拟合，得到的最佳拟合平面即为结构面，并可通过法向量计算对应的结构面产状。

为了识别单条结构面，需要从点云集合中识别出结构面所在平面的空间点簇。本文采用基于密度梯度的聚类算法(Wang et al.，2013)，从上述聚类后的点云集合进行分割提取。具体步骤如下：

(1)初始化，计算密度分布：计算各点的d近邻，以其d近邻的平均距离作为该点的密度。

(2)获取不动点，获得原始聚类：随机选择某一未分类的点O，获取其d近邻中密度最大的点P，根据以下两种情况比较点P与点O的密度：a.当点P密度小于点O密度，即D(P，d)的数值大于D(O，d)的数值时，则点O为一不动点，并赋予新的类别号。b.当点P密度大于等于点O密度时，根据点P的聚类情况进行判断，若该点类别号已经确定，可将此聚类号作为该点的聚类号；若该点类别号没有确定，点P可看作起始点的不动点。确定相应的不动点后，将该不动点的类别号赋予该路径下的所有点，由此继续循环至所有点都进行分类。

(3)调整边界点：选择边界点的d个近邻点的类别号作为该边界点的类别号。

(4)计算边界点对各聚类的分布情况进行合并及分割：将单条结构面所在平面的空间点簇分割提取出来，接下去只需将这些点簇进行平面拟合，即为所需结构面。采用最小二乘法拟合平面获得结构面所在平面的方程：

Ax+By+Cz+D=0

(6)

(7)

如果记：

(8)

那么：

z=a0x+a1y+a2

(9)

式中：a0，a1，a2为方程系数。对于属于一系列的n个点的坐标(xi，yi，zi)，i=1，2，3…n，使用最小二乘法拟合平面，则满足各点到拟合平面的距离平方和S为最小值，S的计算公式为：

(10)

若要使S为最小值，应满足下式：

(11)

联立可得：

(12)

解得：

(13)

通过代入a0，a1，a2即可得到单位法向量的分量。

对结构面进行平面拟合后，即可通过计算结构面的单位的法向量以得到结构面的产状：

(14)

其中：ua，ub，uc为拟合平面单位法向量的分量。

3.3 几何参数获取

几何参数主要是结构面位置、迹长和间距。其中结构面的位置由同组点云集合中的点云坐标决定

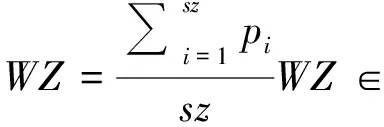
(15)

式中：sz为点云集合中所有点的总数。

Riqueme et al.(2018)将结构面假设成为不规则多边形，并通过计算所有顶点之间的距离以寻求最远距离，此时的最远距离即看作该结构面的迹长，由式(16)计算。

TL=max：ed(pipj)

=‖pi-pj‖2∀i，j∈{1，…，sz}TL，ed∈，

sz∈N

(16)

同时，定义结构面间距为同组中两个相邻结构面之间的法线距离。当结构面理想地彼此平行时，间距可以通过式(17)～式(19)计算。

结构面1：

Ax+By+Cz+D1=0

(17)

结构面2：

Ax+By+Cz+D2=0

(18)

(19)

式中：结构面1和结构面2是两个相邻结构面的平面多项式方程，由单位法向量(A，B，C)和常数参数D1和D2定义，SP12是这两个结构面的间距值。

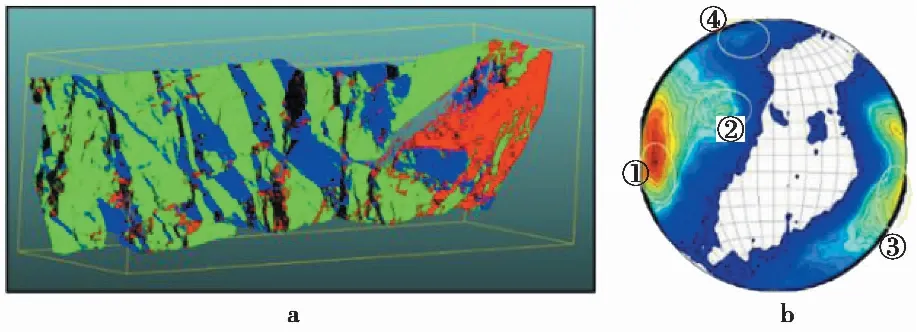
图6 结构面识别结果Fig.6 Structural surface recognition resultsa.Ⅲ-B区120平台露头结构面分组；b.赤平投影(等面积网)

3.4 结构面识别解译结果

利用上述结构面信息识别算法，对Ⅲ-B区域获取到无人机点云数据进行结构面智能识别与解译，结构面识别结果与赤平投影图如图6所示。Ⅲ-B区120m平台的岩体露头存在4组优势结构面：J1：268°∠76°，J2：310°∠40°，J3：115°∠71°，J4：344°∠78°。各组结构面解译后的产状、迹长、间距、密度等几何信息进行统计并分析，如表 2所示。

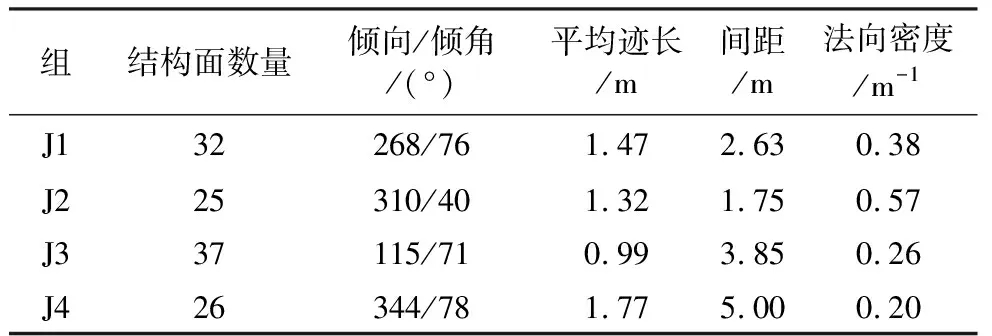
表 2 结构面统计信息Table2 Statistics of discontinuities

对于相同测线位置的结构面识别，算法识别结果和人工量测结果是很相近的(图7)。由于人工测量主观性强，受现场客观条件影响较大，很多结构面信息无法准确提取，因此机器算法所识别的结构面数更多。表 3对比展示了两种方法的量测结果，算法识别结果和人工量测结果倾向倾角角度差值在2°～6°之间；4组结构面的迹长差值在0.14～0.34m之间，间距差值在0.028～0.26m之间。差值均在可接受范围内，证明基于点云数据的结构面识别的精准程度是可靠的。

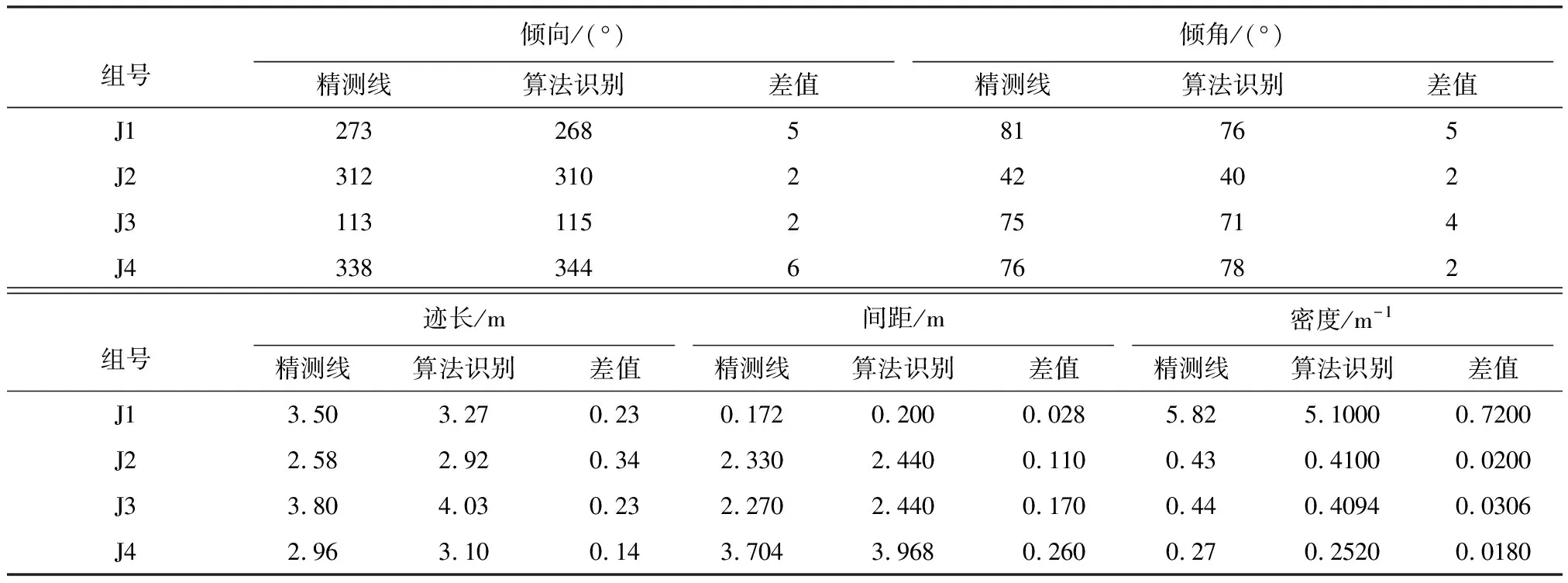
表 3 算法识别与人工量测结果参数对比Table 3 Comparison of result parameters between algorithm recognition and manual measurement

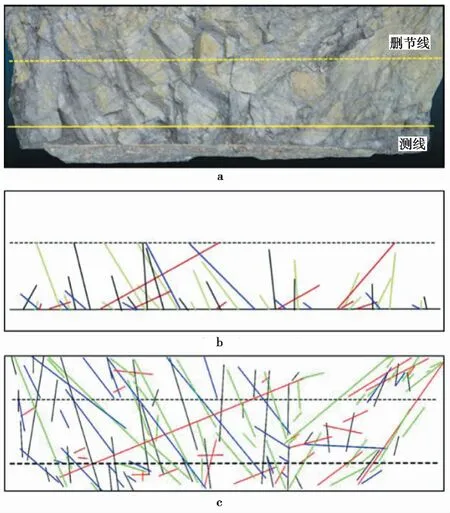
图7 两种测量结果对比Fig.7 Comparison of the measurement results between two methodsa.边坡测线编录剖面；b.人工精测线量测结果；c.算法识别结果

4 三维离散元建模流程

4.1 数值模型建立

作为常用三维离散元软件，3DEC无法直接导入点云数据进行复杂地质体的三维建模。本文借助Rhino软件的三维模型构建技术，结合Griddle软件的网格处理功能实现任意复杂地质体的数值网格模型快速剖分。整个工作过程均支持交互式界面操作，且网格剖分过程体现了高度的自动化特点。因此通过“Rhino-Griddle-3DEC”联合建模方法，可将点云数据导入3DEC完成三维数值建模。具体流程如下：

(1)确定目标对象。本文选取Ⅲ-B区120m平台长18m，高6m的点云模型开展三维数值建模(图8a)。

图8 建模具体流程图Fig.8 Specific flow chart of modeling

(2)初始点云的稀疏处理。在3DEC中将离散裂隙网络(DFN)插入数值模型时，过密的模型网格会导致DFN切割模型失败，因此需要通过对初始点云进行稀疏及优化预处理(图8b)，形成适合后期处理的点云模型。

(3)三角形网格生成与修复。将点云导入Geomagic Studio，点云中的各点以三角网格形式通过相邻边连接起来，达到紧密配合的效果。由于上述过程中可能会产生漏洞、尖锐特征和自相交三角形等错误、多余连接，影响随后的曲面生成和后续计算报错(图8c)。因此在Geomagic Studio中进行封装后需要对曲面进行漏洞修补、平滑及自相交修复，并将修复后的网格模型导入Rhino中(图8d)。

图9 离散网络模型切割后的边坡计算模型Fig.9 Slope calculation model after discrete network model cuttinga.初始离散裂隙网络；b.简化后离散裂隙网络；c.3DEC边坡计算模型

(4)三维实体模型生成。借助Rhino中的RhinoResurf插件完成非均匀有理B样条(NURBS)曲面重构及裁剪(慈瑞梅等，2004)，利用Rhino中的“挤出曲面”和“布尔运算切割”功能，根据现场调查情况设置5m的厚度和底座，形成三维实体模型(图8e)。

(5)3DEC数值模型生成。借助Griddle做水密处理，形成符合不透水定义的封闭曲面后，通过网格剖分得到三维数值模型，最终输出为3DEC可以识别的GVol.3DDAT文件格式并将其导入3DEC软件。如图8f所示，3DEC中边坡数值模型尺寸为18m8m8m，共计生成1737个离散单元体。

4.2 离散裂隙网络生成

3DEC中具有强大的离散裂隙网络(DFN)生成能力。为使DFN生成的结构面圆盘可以成功切割边坡模型且完成计算，离散裂隙网络的范围应稍大于边坡模型，尺寸为20m10m10m。DFN模型特征只受结构面各参数统计分布的影响，包括裂隙尺寸(半径)、产状、位置和密度的分布统计(Zheng et al.，2014；Kong et al.，2020)。

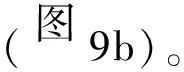
表 4 Ⅲ-B区岩体结构面参数统计Table 4 Statistics of rock mass discontinuities parameters in Ⅲ-B area

4.3 计算结果及分析

3DEC中的本构模型分为块体本构模型和节理本构模型，其中岩石材料设定为理想弹塑性模型，采用Mohr-Coulomb的本构关系(Itasca，2003)。

表 5 Ⅲ-B区120￣￣m平台边坡岩体力学参数Table 5 Mechanical parameters of rock mass in 120m platform of the Ⅲ-B area

上部边界为自由边界，模型四周及底面边界为约束边界。初始地应力天然工况下只考虑自重。根据岩石力学实验数据和现场工程资料，Ⅲ-B区120m平台边坡仅出露千枚岩，未见其他岩性出露，表 5给出了具体的岩石力学参数。

由图10可知，模型计算到6315步时达到平衡，边坡在天然工况下稳定性良好。位移集中在左侧陡坡边缘处，最大位移为0.82mm。变形主要发生在Z轴(竖向)方向，表现为结构面交切形成的楔形体移动，以坡体的沉降为主。在X方向，最大位移发生在坡体临空面，表现为结构面交切形成的楔形体移动，最大位移为0.18mm(方向沿X轴正方向)。在Y方向上，最大位移为0.3mm，为上部坡体向临空面的滑动。综上可知，Ⅲ-B区120m平台边坡的主要位移为竖直方向上的沉降。

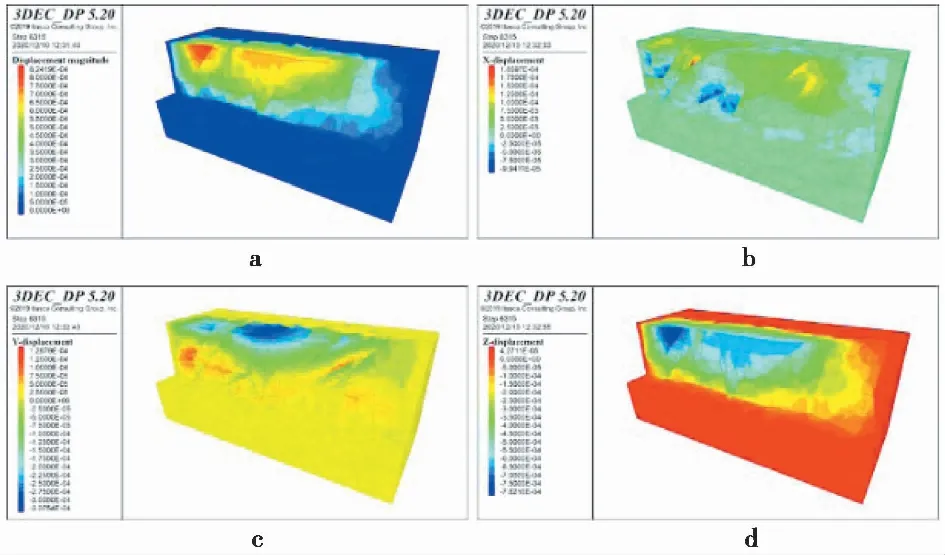
图10 3DEC计算至10000步结果Fig.10 Results when 3DEC calculates to 10000 stepsa.整体位移云图；b.X向位移云图；c.Y向位移云图； d.Z向位移云图

在边坡模型上设置6个关键点，监测其位移随时间的变化规律。图11中的曲线可以看出，监测点的Z向位移曲线都在相对较短的时间内达到稳定状态，不随计算时步变化，即位移时程曲线是收敛的，边坡处于稳定状态。根据离散元强度折减法，利用3DEC的solve fos命令进一步计算安全系数，到12363步时达到临界破坏，此时计算安全系数所得为1.27，验证了天然工况下Ⅲ-B区120m平台边坡稳定性状态良好。

图11 边坡模型监测点布置与监测结果Fig.11 Monitoring points arrangement and the resultsa.监测点位置分布；b.监测点位移-时步曲线

5 结 论

以江西德兴银山铜矿露天高边坡作为工程背景，结合无人机测量与“Rhino-Griddle-3DEC”联合建模方法，利用结构面统计信息构建离散裂隙网络切割边坡模型，实现高陡岩质边坡稳定性的三维离散元数值计算。主要结论如下：

(1)基于SfM三维重构技术建立露天矿山边坡的三维点云模型。通过计算点法向量、聚类分割等算法建立岩体结构几何参数识别与解译方法。对比现场人工测量结果验证了该方法的可靠性。对优势分组，优势产状，迹长分布，间距分布等结构面信息进行统计分析，构建岩体结构表征模型。

(2)提出“Rhino-Griddle-3DEC”的联合建模方法，将三维点云模型导入3DEC中构建边坡三维离散元数值模型。根据岩体结构表征模型建立离散裂隙网络DFN，开展边坡稳定性计算。

(3)本文提出的结构面识别解译方法量测的区域大，且测量过程不影响边坡生产作业。结构面解算精度符合后期进行岩体质量分级或稳定性计算的要求，显著提高了大规模高边坡的岩体编录效率。结合边坡三维点云建模与岩体结构面统计分析，“Rhino-Griddle-3DEC”建模方法能够快速建立岩体结构的三维离散元模型，获得更加符合实际的数值模拟计算结果。