水库型滑坡复合水动力增载位移响应比物理预测模型及其应用*

郭 璐 贺可强 周 云 陈海林 贾世祥

(①宿迁学院 建筑工程学院，宿迁 223800，中国)(②青岛理工大学 土木工程学院，青岛 266520，中国)(③青岛地质工程勘察院(青岛地质勘查开发局)，青岛 266101，中国)

0 引 言

三峡库区是我国滑坡发生频率较高且规模较大的地区，尤其是三峡工程建成后，降雨、库区高水位循环涨落等外界影响因素引起了库岸边坡地下水运行环境的改变，从而降低了库区滑坡的稳定性。多处滑坡在降雨与库水位涨落形成的复合水动力作用下发生失稳破坏，如石榴树包滑坡、黄土坡滑坡、千将坪滑坡、白家包滑坡、卧沙溪滑坡等，上述滑坡在给库区人民生命财产安全造成巨大威胁的同时，也使三峡工程的长期安全运行受到了挑战。因此，研究和建立降雨和库水耦合动力条件下水库型边坡的灾变预警预测方法，对三峡工程库区以及其他类似水动力环境条件库区滑坡的预测预报和防治都将具有重要的理论意义与应用价值。

目前，水库型滑坡稳定性评价与预测方法主要为极限平衡法和位移时序预测法。其中，极限平衡法为静态评价模型，只能对水库型滑坡进行静态稳定性计算，而无法对外界水动力变化条件下的边坡动态稳定性进行分析与评价；而位移时序预测法是一种通过观测降雨量、库水位与边坡位移随时间变化，建立位移监测预报模型对边坡进行动态稳定性分析与监测预警的方法，由于该类方法具有监测数据容易获取且误差低等特点，使得该类方法在边坡稳定性评价与监测预警领域得到了广泛应用。自日本学者Saito(1965)提出“斋腾模型”以来，国内外许多学者在寻找滑坡位移动态规律以及滑坡体稳定性预测预报方法，并建立了大量的滑坡预报模型，概括起来主要包括以下3类预报模型：(1)统计分析预报模型(陈明东等，1988；苏爱军等，1990；贺小黑等，2013；Cui et al.，2015；邓洪高等，2019；Park et al.，2019；亓星等，2019；Zhang et al.，2020)；(2)非线性预报模型(张倬元等，1988；秦四清等，1993；龙辉等，2002；贺可强等，2009；许强等，2009；谈小龙等，2010；韩贺鸣等，2019)；(3)综合预报及多源信息预报模型(钟荫乾，1995；李东山等，2003；万全等，2005；Cai et al.，2015；许强等，2020；朱崇浩等，2020；刘艳辉等，2021；罗路广等，2021)。上述位移时序预测模型大多只能反映边坡位移随时间的演化规律，而无法解释导致边坡位移变化的力学动因，且位移变化与边坡稳定性之间没有明确的一一对应关系。尤其对边界与动力条件复杂的水库型堆积层滑坡而言，由于受汛期降雨及周期性库水循环涨落等动力因素控制，其滑坡位移常出现多期非失稳的加速阶梯状振荡变化，这并不意味着滑坡会整体失稳，仅以该特征判定边坡稳定与否，容易导致大量误判。而且该类方法失稳判据所依据的位移及位移速率并不统一，其临界位移参数因滑坡的形态、水动力条件与坡体岩土力学性质的不同而有显著差异(表 1)

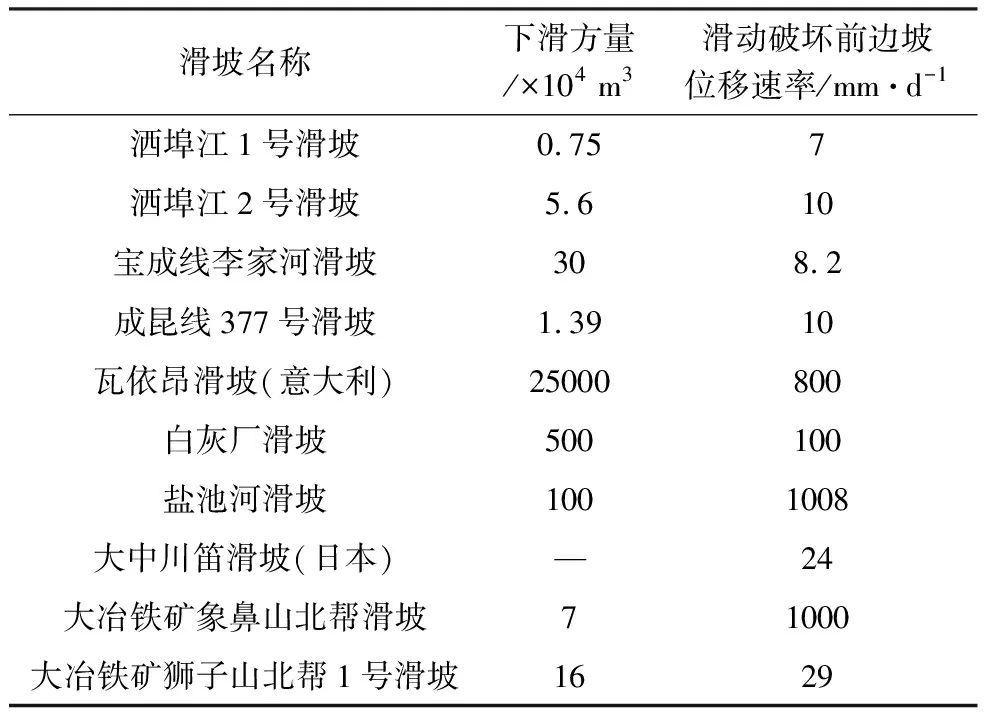
表 1 国内外某些重大滑坡滑动前位移速率(贺可强，2016)Table1 Displacement rates of some major landslides at home and abroad before sliding(He，2016)

(贺可强，2016)，因而该类方法无统一的失稳判据。作为非线性预报的位移动力学新方法，动力增载位移响应比参数与预测模型近年来得到了广泛应用。动力增载位移响应比参数主要用于研究非线性系统失稳前兆和失稳预报，诸多学者通过对滑坡的非线性动力学过程与特征进行系统研究，揭示了该参数的基本性质与边坡稳定状态的定量关系，为该类滑坡物理预测模型的建立开辟了一条新的研究途径。贺可强等(2015，2017b)首次将动力增载位移响应比物理预测参数与模型应用到滑坡预警领域，并在不断地应用研究中建立了水库型堆积层滑坡的降雨、库水位动力增载位移响应比物理预测参数与模型，推进了该参数与模型在滑坡稳定性评价与监测预警领域的应用；傅鹏辉(2017)运用库水动力增载位移响应比参数与模型，研究了库水位下降对八字门滑坡稳定性的影响，发现该参数变化与边坡稳定性演化规律具有负相关关系；包放歌(2019)以开挖边坡水平应力和位移分别作为动力增载量和响应量，建立了边坡开挖动力增载位移响应比预测模型，并运用该模型评价了采动卸荷条件下金川石英石矿山边坡的稳定性。田野(2021)建立了以地下水相对高度为增载量、对应抗滑桩桩间土体水平位移为响应量的动力增载位移响应比模型，并将其应用于返岭前滑坡，论证了采用动力增载位移响应比评价边坡-抗滑桩体系稳定状态的可行性。上述研究表明动力增载位移响应比预测模型在滑坡的位移动力学研究过程中已得到了广泛应用。然而当前该预测模型的研究都是以降雨或库水等单一水动力变量进行动力增载位移响应比计算，而对于水库型堆积层滑坡而言，库水位变化和降雨形成的复合水动力影响无疑是控制滑坡失稳破坏的主要因素，因此滑坡的动力增载效应应包括这两种因子的叠加效应。如何根据水库型滑坡复合水动力条件与位移变化规律对其稳定性进行有效评价与预测还有待于进一步研究。

鉴于当前水库型滑坡预测方法的不足和局限性，本文在综合分析水库型滑坡位移变化特征与降雨量及库水位变化动力因素关系的基础上，提出与确定了降雨与库水动力转换系数k的计算方法，以此为依据将降雨动力与库水动力这两种不同的水动力增载效应进行了有机耦合叠加，建立了复合水动力增载参数的计算方法。在此基础上，提出将复合水动力变化量及其位移变化量分别作为动力增载及其响应参数，依此建立了水库型滑坡复合水动力增载位移响应比物理预测模型，揭示了水库型滑坡复合水动力增载位移响应比参数与滑坡稳定性之间的对应关系，并验证了运用该参数对水库型滑坡进行动态稳定性评价与监测预警的可行性。

1 动力增载位移响应比物理预测参数的可行性探讨

滑坡形成和发展过程包含着滑移面的形成、延伸、连通、位错等一系列环节，该过程本质上是坡内的岩土体单元由于受到外力的持续作用而产生的相对位移累积到一定程度而引起的坡体突然失稳的过程(张学言等，2003)。从宏观上说，由于外力作用，滑动面处岩土体逐渐损伤，这种损伤的加剧和累积在达到一定规模之后会突然引起边坡失稳。因此，滑坡受力形变与稳定性演化规律的研究，要以岩土体材料为受力单元，分析其应力-应变关系及变形与破坏规律。

1.1 滑坡动力增载位移响应率参数及其变化特征

由三轴应力作用下岩土体的本构曲线(图1)可知，在三轴拉伸和压缩条件下，岩土体单元应力-应变曲线将经历以下4个阶段：(1)受力单元在OA阶段处于压缩变形状态，应力-应变曲线大致成一条直线，在该阶段几乎不产生塑性变形，经过一轮加卸载过程后，受力单元能够基本恢复原状；(2)当外力继续增大，岩土体受力单元的应力-应变曲线则进入了AB阶段，即弹性变形阶段。在该阶段完全不产生塑性变形，经过一轮加卸载过程后，受力单元能够完全恢复原状。此阶段内应力-应变曲线为直线，其应变与应力变化量Δε与Δσ成正比例关系，设比例系数为λ；(3)随着外力的继续增大，当进入BC阶段，材料开始产生塑性变形，应力-应变曲线呈现出上凸的形态，应力变化量Δσ与应变的变化量Δε呈非线性关系。若记此阶段内应变与应力变化量Δε与Δσ之比为λ，则随着应力的增加，λ逐渐增大；(4)随着外力进一步增大，受力单元的材料损伤进一步积累，当应力增至D点时，材料完全破坏，其应变变化量Δε与应力变化量Δσ的比例系数λ将趋向于无穷大。

图1 三轴应力作用下岩土体的本构曲线Fig.1 Constitutive curve of rock and soil mass under triaxial stress

岩土体受力单元的应力-应变曲线与破坏规律表明，作为一个非线性系统，材料在完全失稳破坏之前，可以将其应变变化量Δε与应力变化量Δσ的比例系数λ作为其稳定性状态与趋近失稳的定量表征，故定义该比例系数λ为动力增载位移响应率，其数学表达式为：

(1)

式(1)描述了在外力作用下，非线性系统应变对应力变化的响应程度。即使所受荷载为常量，系统响应程度也会随着本身稳定状态的不同而有所差别。边坡作为典型的非线性系统，其在发育过程中所受到的诸多外界因素，如降雨、库水波动、人类因素等，坡体在受到这些外力作用后，会产生应变和位移等响应结果，因此在边坡稳定性研究过程中，可记上述外力作用为边坡受到的广义荷载P，记坡体受到广义荷载后产生的系统响应为R，由岩土体的应力-应变曲线可推演出边坡稳定性演化过程中的动力荷载与响应的关系曲线，如图2所示。

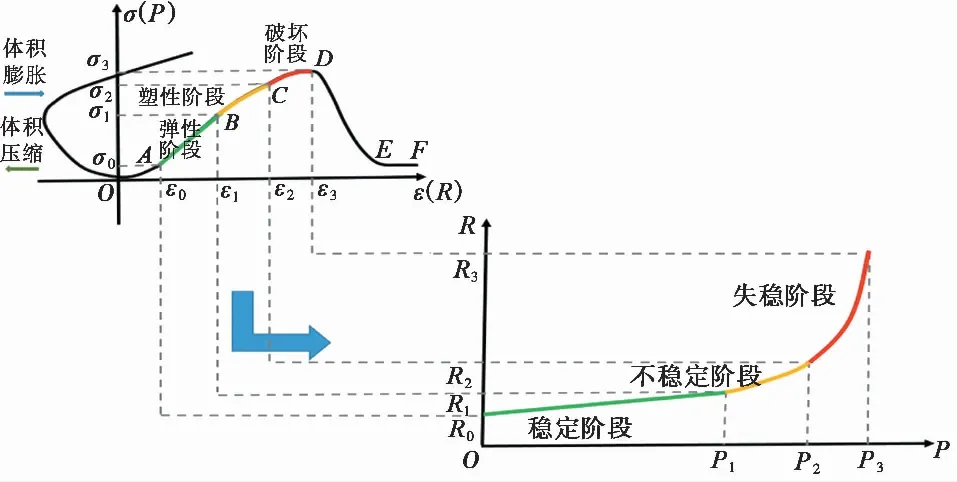
图2 滑坡演化过程中荷载与响应关系Fig.2 The relationship between load and response during the evolution of landslide

设滑坡所受广义荷载变化量为ΔP，受荷载作用的响应变化量为ΔR，则系统受荷载作用而产生的动力增载位移响应率λ可定量表示为：

(2)

由边坡荷载与响应的关系(图2)，滑坡所受广义荷载时的过程可分为初始弹性加载变形和塑性加载变形两种情况，分别记λ0为初始阶段动力增载位移响应率、λt为t时刻动力增载位移响应率。由此可将坡体受到荷载加载作用至失稳破坏划分为以下3个阶段：

(1)当系统处于稳定阶段，t时刻动力增载位移响应率与初始阶段动力增载位移响应率相等，即λt=λ0。

(2)当系统处于塑性不稳定阶段，t时刻动力增载位移响应率大于初始阶段动力增载位移响应率，即λt>λ0。

(3)当系统处于失稳阶段，t时刻动力增载位移响应率λt→∞。

1.2 滑坡动力增载位移响应比参数特性

根据弹塑性力学基本原理，动力增载位移响应比是刻画和反映非线性系统稳定性变化的一种物理评价参数，其值为系统动力响应率与其初始动力响应率之比。定义动力增载位移响应比为其t时刻动力增载位移响应率λt与其初始变形阶段内的动力增载位移响应率λ0的比值，其数学表达式为：

(3)

式中：ΔRt为t时刻增载响应量；ΔR0为初始变形阶段增载响应量；ΔPt为t时刻动力增载量；ΔP0为初始变形阶段动力增载量。

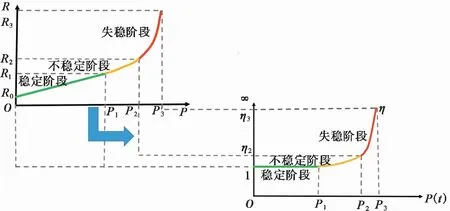
图3 边坡演化过程中动力增载位移响应比变化曲线Fig.3 Variation curve of displacement response ratio of dynamics increment during slope evolution

由边坡荷载与响应的关系(图2)及动力增载位移响应比参数的定义，可以推演出边坡演化过程中其动力增载位移响应比曲线的变化规律(图3)。从图3可以看出，动力增载位移响应比参数(η)值取决于非线性系统的稳定程度，当系统处于稳定阶段，η=1；当系统处于塑性不稳定阶段，η>1，其不稳定程度取决于动力增载位移响应比偏离1的差值；当系统处于失稳阶段，η→∞。

上述分析可知，动力增载位移响应比参数(η)是非线性系统位移与动力耦合物理评价参数，其变化特征反映了其系统稳定性变化规律，而且与稳定性具有一一对应的关系，因此该参数是刻画和反映其稳定性演化的物理评价参数；此外，该参数可有效揭示非线性系统稳定性与灾变机理，其大小仅取决于系统稳定性变化，而不受动力变化影响，因而更具有系统稳定性演化与突变的预测预报功能。因此，可运用该物理预测参数对边坡进行稳定性评价与失稳预警。

2 水库型滑坡复合水动力增载位移响应比物理预测模型研究

2.1 滑坡动力增载及其响应参数的选择与分析

边坡从稳定到失稳的过程中会经历滑移面的产生→扩展→贯通→位错等一系列损伤过程。这些过程不仅在微观尺度，而且在宏观尺度上也具有相互作用的关系，加之各种外界动力影响因素的共同作用，导致不同区域、不同类型以及不同规模的滑坡加载作用机制和变形规律存在巨大差异。由此，采用动力增载位移响应比预测参数与模型对滑坡进行有效预报时，需要解决如何对滑坡施加和进行动力加载、如何确定和量化滑坡加载与其响应参数以及如何确定滑坡加载与其响应变化周期这3个问题。

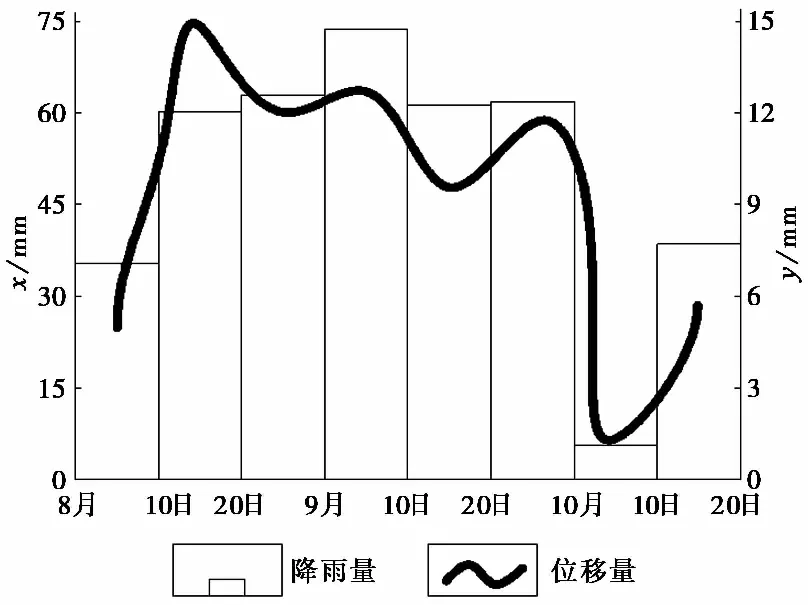
图4 石庙滑坡位移量与降雨量对比图(王发读，1995)Fig.4 The displacement curves with the rainfall of Shimiao Landslide(Wang，1995)

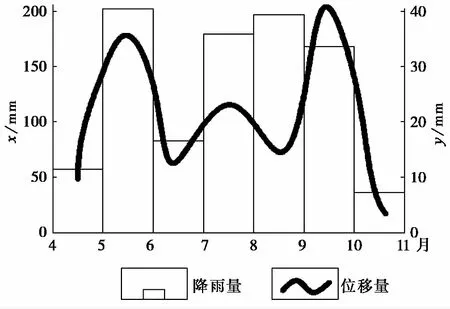
图5 李家湾滑坡位移量与降雨量对比图(王发读，1995)Fig.5 The displacement curves with the rainfall of Lijiawan Landslide(Wang，1995)

三峡库区堆积层滑坡具有孔隙大与透水性强的特点，因此当持续而集中的降雨发生时，雨水快速入渗滑体内部，加速滑面的贯通。因此，降雨量的变化应作为滑坡动力增载计算的重要动力参数。根据三峡库区降雨规律及对堆积层滑坡作用特点，降雨无疑对堆积层边坡起增载作用。降雨诱发堆积层滑坡的位移动力学特征主要取决于由降雨引起的地下水环境的变化，而且滑坡位移与其有效降雨量存在着一一对应关系(图4、图5)，即滑坡位移量和位移速率与降雨变化量之间具有明显的一致性和较好的相关关系(王发读，1995；贺可强等，2017a)。因此可以以单位时间降雨量 ΔJ作为动力增载参数。同时，对于水库型滑坡这一特殊类型滑坡而言，库水位的周期性循环涨落也是边坡失稳的主要动因，其库水动力效应主要由滑坡体渗透系数的大小决定。根据不同渗透系数的滑坡分类，可将三峡库区水库型滑坡分为动水压力型滑坡、浮托减重型滑坡、动水压力与浮托减重复合型滑坡3种类型(向玲等，2014)。

对于三峡库区滑坡而言，其大部分滑坡为动水压力型滑坡。动水压力型滑坡的特点是：滑坡体渗透系数相对较小，当库水位上升时，由于库水渗入滑坡内部速度小于库水上升速度而产生水头差，并产生了指向滑体内的动水压力，使滑坡稳定性提高；当库水位下降时，由于库水从滑体内部渗出速度小于库水下降速度而产生水头差，产生了指向滑体外的动水压力，使滑坡的稳定性降低，滑坡的位移变化也多在此阶段产生。因此，对动水压力型滑坡而言，库水位下降也是其动力增载的主要因素。贺可强等(2017b)研究了动水压力型滑坡位移变化量与库水下降的关系，结果表明在堆积层坡体物理力学参数、坡角等因素相对不变的情况下，动水压力型水库边坡的位移变化量直接受库水动力变化的影响与控制，且位移变化量与库水位的变化规律具有较好的相关关系。故可将单位时间内库水位下降量ΔH作为其动力增载参数。鉴于滑坡监测信息多以地表位移监测为主，可以通过监测得到单位时间位移(位移速率，位移加速率)变化量ΔS作为库水位与降雨增载产生的响应参数。由于边坡的变形破坏具有阶段性，处于不同稳定阶段的边坡，其距离失稳的时间并不相同。因此，加载周期的选取应根据滑坡所处的变形破坏阶段进行确定。李天斌等(1999)将滑坡预报归并为中长期预报和短临预报两类。对于处于相对稳定变形阶段的边坡，可对边坡进行中长期预测预报，选择以年为加载周期，以月为单位统计加载及其响应参数监测值；对于处于加速变形阶段的边坡，应对边坡进行短临预报，选择以月为加载周期，以日为单位统计加载及其响应参数监测值；也可以选择以日为周期，以小时为单位统计加载及其响应参数监测值。

2.2 滑坡复合水动力增载位移响应比参数及其物理预测模型

2.2.1 滑坡复合水动力增载效应及评价参数研究

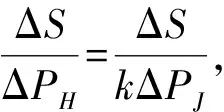
ΔP=ΔH+kΔJ

(4)

从式(4)可以看出，要准确确定降雨与库水耦合增载作用下的复合水动力ΔP的大小，其首要任务是确定出降雨与库水动力转换系数k。根据前述分析，复合水环境下水库型滑坡位移是由降雨和库水增载作用的共同结果，可认为水库型滑坡位移变化量为降雨动力引起的位移变化量和库水动力引起的位移变化量之和。因此可将库水位变化量作为库水动力增载参数、降雨变化量作为降雨动力增载参数，将总位移变化量作为降雨和库水复合动力作用的响应参数。在边坡处于初始复合水动力增载基准周期时，此时可认为边坡基本处于弹性稳定阶段，其单位降雨量导致的边坡位移变化量及单位库水位变化量导致的边坡位移变化量均为一定值。为此，本文提出通过选定一个初始复合水动力增载基准周期，运用滑坡远程自动化实时监测系统分别监测水位下降过程中降雨变化量ΔJ0、库水位变化量ΔH0及其引起的位移变化量ΔS0。分别定义单位降雨量引起的位移量与其的比值为降雨动力增载位移响应率ηJ、单位库水位下降量引起的位移量与其的比值为库水动力增载位移响应率ηH，其降雨量、库水位下降量与边坡位移变化量之间的关系为：

ηJΔJ0+ηHΔH0=ΔS0

(5)

由式(5)可以看出，只要知道任意两组ΔJ0、ΔH0与ΔS0的监测数据，即可求得一组ηJ与ηH值。基于此，本文定义初始降雨动力增载位移响应率与库水动力增载位移响应率的比值为降雨与库水动力转换系数k，即：

(6)

进而将式(6)代入式(4)即可确定单位时间内边坡复合水动力参数ΔP的大小。式(4)～式(6)表明：在确定单位降雨量ΔJ及库水位下降量ΔH及降雨与库水动力转换系数k的基础上，即可准确确定单位时间内水库型滑坡复合水动力增载参数ΔP的大小。通过将t周期内每个单位时间的复合水动力增载量ΔP进行累加，即可求得滑坡t周期的复合水动力增载量ΔPt。

2.2.2 滑坡复合水动力增载位移响应比物理预测模型

根据前述研究，将初始周期与t周期复合水动力增载量分别记为ΔP0与ΔPt，将初始周期与t周期内复合水动力增载引起的位移响应量分别记为ΔS0与ΔSt。在上述复合水动力增载及其响应参数确定的基础上，本文针对水库型滑坡降雨与库水形成的复合水动力作用特点，建立了复合水动力增载位移响应比物理预测模型表达式如下：

(7)

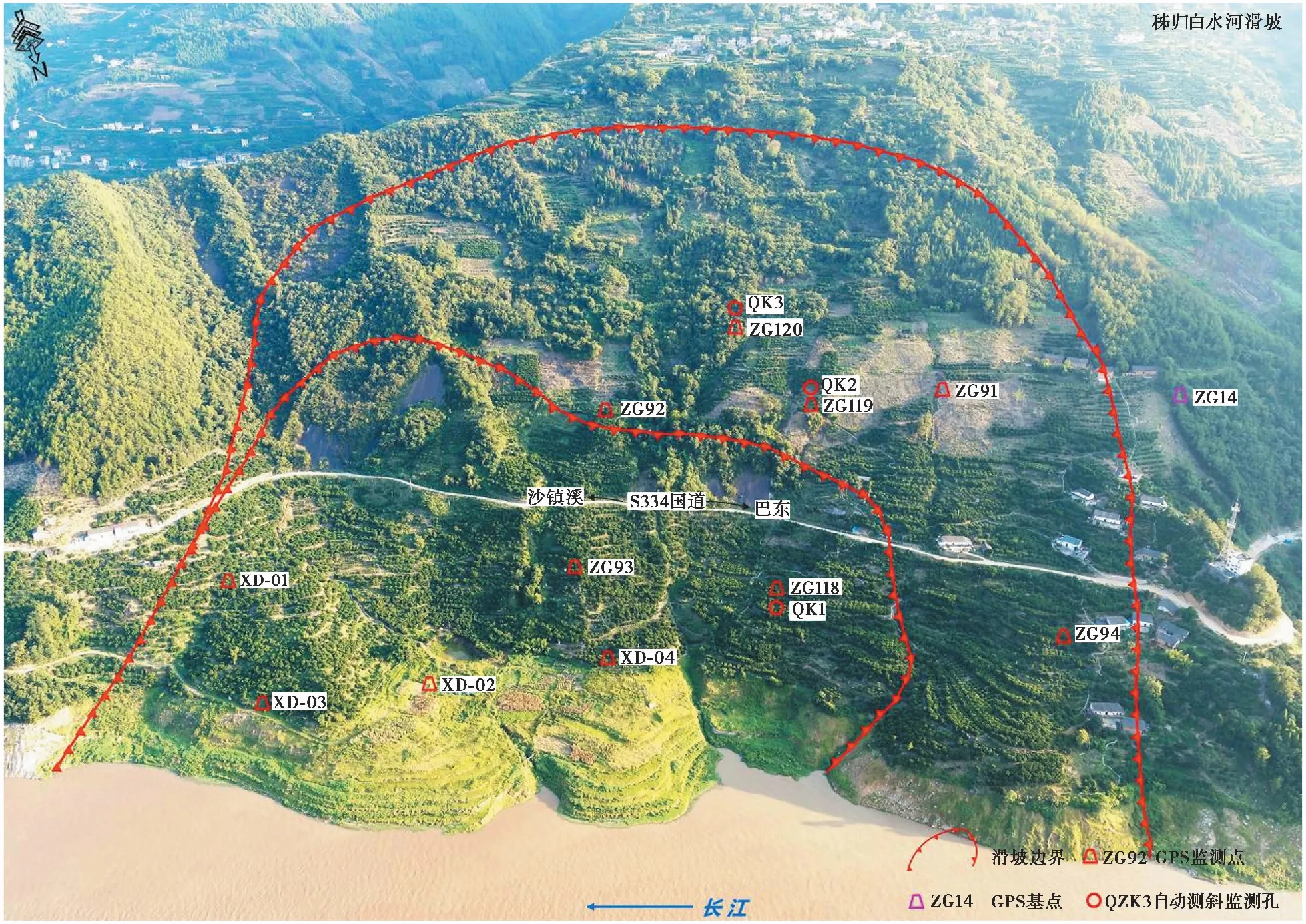
图6 白水河滑坡监测点布置图(图片来源于湖北长江三峡滑坡国家野外科学观测研究站)Fig.6 The layout of Baishuihe Landslide monitoring points

式中：ΔSt为t周期复合水动力增载响应量；ΔS0为初始周期复合水动力增载响应量；ΔHt+kΔJt为t周期复合水动力增载量；ΔH0+kΔJ0为初始周期复合水动力增载量。

3 实例分析

3.1 白水河滑坡概况

白水河滑坡位于长江南岸沙镇溪镇白水河村，距三峡大坝56km。该滑坡为典型的动水压力型堆积层滑坡，滑坡长600m，宽700m，体积1260×104￣￣m3，其地质全貌及监测点布置如图6所示。滑坡主滑方向20°，后缘高程350m，前缘高程120m。该滑坡主要由滑体、滑带、滑床3部分组成，粉质黏土以及碎块石土是形成滑体的主要物质，滑带土体以粉质黏土为主，处于堆积层与基岩的夹层中，其工程地质剖面图如图7所示(孙一清等，2019)。

白水河滑坡自2003年6月三峡库区蓄水至135m水位后开始监测。根据宏观变形和GPS监测数据，其滑坡后缘变化较小，前缘变化较大。主要原因是前缘处于145～175m库水位涨落范围内，库水位周期性循环涨落及汛期降雨引起坡体动静水压力的骤变是引起该边坡前缘变形的主要因素。

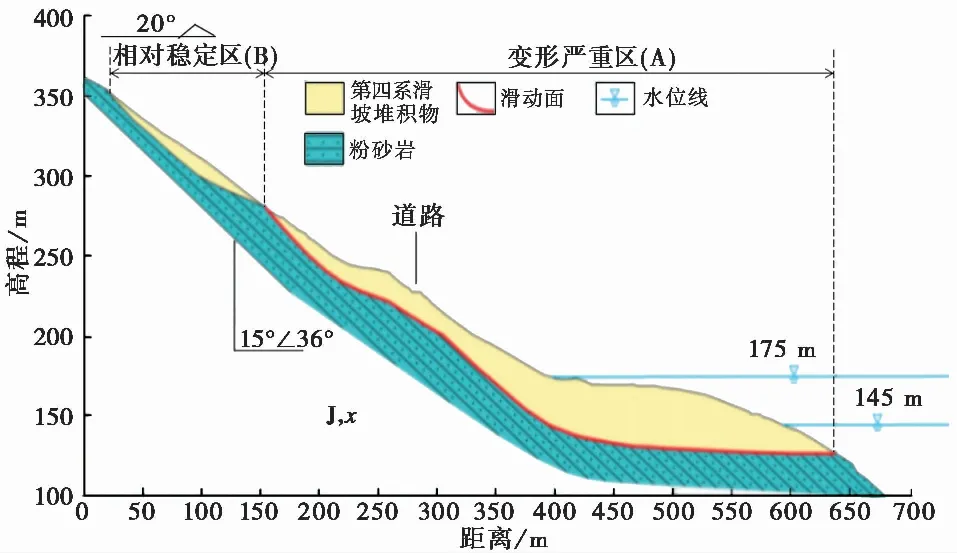
图7 白水河滑坡工程地质剖面图(孙一清等，2019)Fig.7 Engineering geological profile of Baishuihe landslide(Sun et al.，2019)

3.2 白水河滑坡稳定性及其影响因素分析.

3.2.1 白水河滑坡变形及其动力影响因素分析

根据湖北长江三峡滑坡国家野外科学观测研究站监测的白水河滑坡降雨量、库水位及变形严重区ZG93、ZG118监测点位移数据(图8)，三峡库区库水位从2006年10月逐渐升至155m左右，2008年9月汛期过后，库水位进一步升高至175m附近。此后库水位每年在145～175m间大幅波动。2006～2011年库水位涨落期间，其位移时序曲线呈典型的“阶梯状”增长，共有5次较大变形。由白水河滑坡累积位移与库水位变化及降雨量关系曲线可以看出：降雨对滑坡变形有着显著影响。三峡库区每年5～8月汛期期间库水位保持在145m附近，但由于降雨量的增加，白水河滑坡的变形量也显著增加。如2007年5月至8月期间，降雨量为651.29mm，滑坡ZG93监测点与ZG118监测点位移量分别达到了762.1mm及836.9mm；2008年7月至9月期间降雨量为641.4.6mm，滑坡ZG93监测点与ZG118监测点位移量分别达到了249.3mm及271.7mm；2011年7月至8月期间降雨量为325.8mm，滑坡ZG93监测点与ZG118监测点位移量分别达到了108.8mm及100.7mm。总体来看降雨是滑坡变形的重要影响因素，其降雨量与滑坡位移变化关系呈正相关。

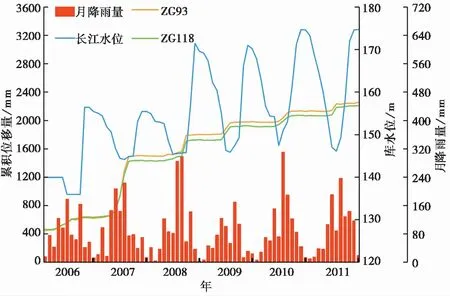
图8 白水河滑坡累计位移与降雨量及库水位关系曲线(数据来源于湖北长江三峡滑坡国家野外科学观测研究站)Fig.8 The relationship curve between the cumulative displacement of Baishuihe Landslide，rainfall and reservoir water level

另外，库水位周期性的变动也对白水河滑坡的变形产生一定的影响。由图8可以看出，2007年2月至7月，由于库水位首次上升至中水位后从155.3m下降至143.9m，滑坡位移大幅增加，其ZG93监测点与ZG118监测点位移量分别达到了600mm和665.6mm；2008年11月至2009年7月，库水位从172.8m下降至145.3m，ZG93监测点与ZG118监测点位移量分别增加了204.5mm与176mm。白水河滑坡在经过2007年从中水位到低水位的位移大变形之后，此后的每年从高水位降至低水位过程中对库水位涨落具有了一定适应性，因此其2007年之后各年滑坡位移量小于2007年位移量。自2009～2011年，每当库水位从175m附近的高水位降至145m低水位，滑坡ZG93监测点与ZG118监测点位移曲线均会出现不同程度的阶跃式上升。因此，库水下降也是诱发白水河滑坡位移变化的重要影响因素。

上述分析表明：白水河滑坡监测点变形及稳定性受每年周期性库水位下降及降雨的双重影响，可以认为该滑坡的动力增载过程是由降雨及库水位的周期性下降来完成的。

3.2.2 白水河滑坡稳定状态分析

从白水河滑坡地表变形及张拉裂缝变化特征来看，2003年6月，三峡水库水位首次上升至135m，该滑坡东侧坡体中前缘位置出现了横向拉张裂缝，表明滑坡变形开始启动；2007年是该滑坡位移变化最大的一年，其滑坡东侧及后缘边界裂缝扩展；在经历2007年大变形之后，每年滑坡变形虽然在降雨集中及库水位骤降的月份有一定幅度的增加，但之后均恢复到蠕滑变形发展状态。至2011年滑坡裂缝还没出露完整，只有东侧裂缝相对贯通，还未形成整体滑动边界(夏园园，2017；易庆林等，2017)。因此，从滑坡演化的时间和空间角度进行分析，白水河滑坡在2011年时还没有处于加速变形阶段。综上所述，尽管白水河滑坡在2006～2011年监测期间出现了多次阶梯状振荡变化，但这些变化都是由于外界水动力条件的变化所导致的，该滑坡仍处于基本稳定阶段。

根据曹阳健等(2016)的研究结果，白水河滑坡2006～2011年间的稳定性系数时序变化曲线如图9所示。由图9可以看出：白水河滑坡在2006年边坡稳定性系数为1.13，此时边坡处于稳定阶段；2007年因为三峡水库首次蓄水至156m这一较高水位后，其首次大幅度下降对滑坡稳定性影响较大，主要原因是库水改变了白水河滑坡抗滑段范围内的坡体物质组成及渗流场分布，降低了滑带下部抗滑段坡体的抗剪强度，导致该边坡稳定性突然降低，边坡稳定性系数降至1以下；2008～2011年白水河滑坡对库水位周期性涨落具有了一定适应性，其边坡稳定性系数开始逐年回升至1.05。其稳定性系数变化规律与白水河滑坡张拉裂缝变化特征与实际稳定状态相吻合。

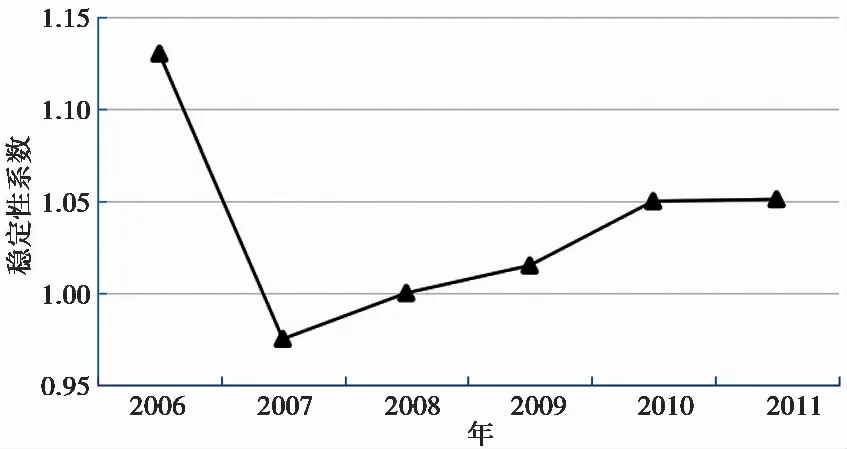
图9 白水河滑坡稳定性系数随时间变化曲线(曹阳健等，2016)Fig.9 Time-dependent curve of stability coefficient of Baishuihe Landslide(Cao et al.，2016)

3.3 白水河滑坡动力增载位移响应比分析与评价

本文选取2006～2011年间白水河滑坡的监测降雨量、库水位和该滑坡变形严重区最具有代表性的ZG93和ZG118两个监测点累计位移量监测数据(图8)为分析依据。根据本文提出的复合水动力增载参数ΔP的计算步骤(式(4)～式(6))，分别选取2006年2～4月库水位不变时降雨变化量ΔJ与位移变化量ΔS以及2006年全年降雨变化量ΔJ、库水位下降量ΔH及其引起的位移变化量ΔS数据，由式(5)和式(6)分别求得ZG93监测点处降雨-库水动力转换系数k=0.028，ZG118监测点处降雨-库水动力转换系数k=0.010。通过式(4)计算出各周期复合水动力增载量的大小(表 2)。在上述计算基础上，选取2006年降雨量与库水位下降量形成的复合水动力变化量作为滑坡初始周期动力增载参数ΔP0，其相应的位移变化量作为复合水动力增载位移响应参数ΔS0，选取2006年之后每年的降雨量与库水位下降量形成的复合水动力变化量作为该滑坡的复合水动力增载参数ΔPt，将相应的位移变化量作为复合水动力增载位移响应参数ΔSt，其计算结果见表 2。根据水库型滑坡复合水动力增载位移响应比评价模型(式(7))，确定该滑坡监测点ZG93和ZG118在不同年份所对应的复合水动力增载位移响应比值，计算结果见表 3。其监测点动力增载位移响应比变化曲线见图10。

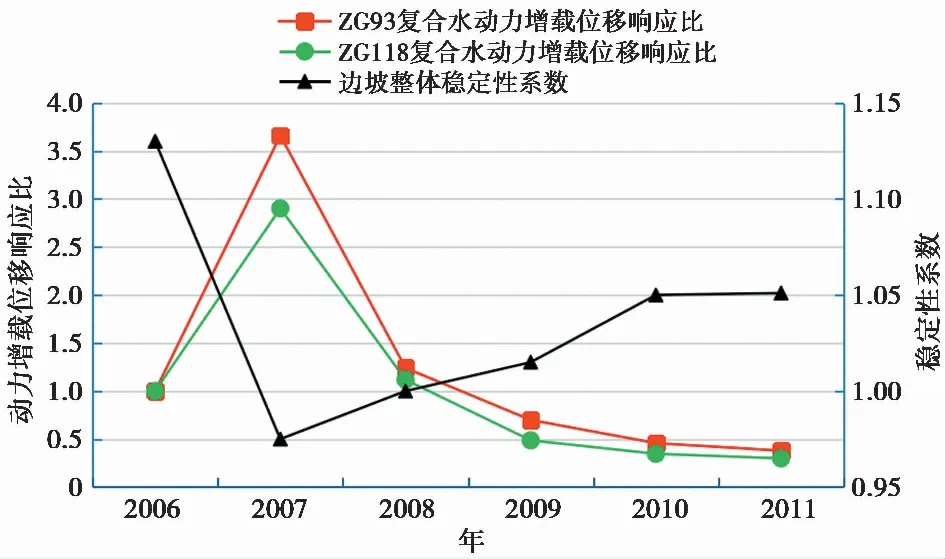
图10 白水河滑坡动力增载位移响应比与稳定性系数变化对比曲线Fig.10 Comparison curve of displacement response ratio of dynamics increment and stability coefficient of Baishuihe landslide

表 3 白水河滑坡ZG93与ZG118监测点动力增载位移响应比计算值Table3 Calculated value of displacement response ratio of dynamics increment at monitoring points ZG93 and ZG118 of Baishuihe Landslide

对比分析白水河滑坡ZG93与ZG118监测点复合水动力增载位移响应比的变化曲线与稳定性系数的关系(图10)，可以看出：白水河滑坡在2006年处于稳定状态时，其动力增载位移响应比等于1；2007年受首次库水大幅下降影响，边坡稳定性系数突然降至1以下时，其ZG93与ZG118监测点的动力增载位移响应比分别达到了3.66和2.90，均远大于1；2008～2011年边坡处于基本稳定状态，稳定性系数从1逐年回升至1.05附近，其监测点动力增载位移响应比均在1附近上下波动。上述分析结果表明：动力增载位移响应比演化规律与实际边坡的稳定状态相吻合，其复合水动力增载位移响应比参数与边坡稳定性系数间存在较好的负相关关系，即当边坡复合水动力增载位移响应比等于1或小于1时，其对应的稳定性系数较大，边坡处于稳定状态；当边坡复合水动力增载位移响应比大于1，且不断增大时，其对应的稳定性系数也相应降低，边坡处于不稳定演化阶段。

4 结 论

通过上述分析研究，可以得出以下结论：

(1)动力增载位移响应比参数(η)是非线性系统位移与动力耦合物理评价参数，其变化特征反映了其系统稳定性变化规律，而且与稳定性具有一一对应的关系，因此该参数是刻画和反映其稳定性演化的物理评价参数。 此外，该参数可有效揭示非线性系统稳定性与灾变机理，其大小仅取决于系统稳定性变化，而不受动力变化影响，因而更具有系统稳定性演化与突变的预测预报功能。

(2)水库型滑坡复合水动力增载位移响应比物理预测参数与模型综合考虑了降雨与库水动力对边坡位移及稳定性的影响，该参数与预测模型不仅可描述水库滑坡稳定性演变及其位移变化的动因与机制，而且还可对该类滑坡的动态稳定性进行定量监测与评价。因此，可运用该物理预测参数对边坡进行动态稳定性评价与失稳预警。

(3)三峡库区典型动水压力型堆积层滑坡-白水河滑坡的稳定性后验分析结果表明：动力增载位移响应比演化规律与实际边坡的稳定性状态相吻合，其复合水动力增载位移响应比参数与边坡稳定性系数间存在较好的负相关关系，即当边坡复合水动力增载位移响应比等于1或小于1时，其对应的稳定性系数较大，边坡处于稳定状态；当边坡复合水动力增载位移响应比大于1，且不断增大时，其对应的稳定性系数也相应降低，边坡处于不稳定演化阶段。因此，该位移动力参数与预测方法是水库型滑坡中、短期预测预报的一种较为有效的物理预测参数与评价方法。