考虑剪力滞的波形钢腹板连续曲线箱梁内力求解方法

杨美良,袁以鑫,钟扬,樊林杰,刘阳帆

（1. 长沙理工大学 土木工程学院，长沙 410114；2. 湖南机场建设指挥部，长沙 410114）

近年来，波形钢腹板箱梁因具有自重小、可以提高底板的有效预应力等优势正不断地被应用到实际工程中。然而，现在关于波形钢腹板箱梁的研究工作大多围绕直线梁，对曲线梁的研究仍然存在很大不足。仝波等[1]推导了波形钢腹板曲线箱梁（CCBG(CSWs)）的弯扭耦合计算公式，并得到了CCBG(CSWs)简支结构的简化求解公式；杨丙文等[2]基于力法对在恒载和活载作用下的三跨等截面连续波形钢腹板曲线箱梁进行研究，得到了波形钢腹板连续曲线箱梁的边中跨合理比值；田宝升[3]依据乌曼斯基纵向翘曲位移理论，考虑曲梁弯扭耦合影响，推导了CCBG(CSWs)简支结构的约束扭转控制微分方程；杜勋[4]通过能量法得到了CCBG(CSWs)简支结构的约束扭转微分方程，并依据伽辽金法得到该方程的求解解析式，最后通过力法提出了多跨波形钢腹板连续曲线箱梁的受力求解方法；刘蓓[5]基于能量变分法，考虑剪力滞、弯扭耦合以及剪切畸变等影响推导了弹性阶段CCBG(CSWs)简支结构的约束扭转控制微分方程。在对CCBG(CSWs)简支结构的横截面翼板纵向位移分析中，已有研究要么忽略了剪滞效应引起的翘曲位移[4]，要么在竖向弯曲位移中忽略了竖向剪力产生的剪切变形影响[5-6]；而对于波形钢腹板连续曲线箱梁的研究均未考虑剪力滞的影响，且在内力分析求解过程中还是基于传统力学方法，给计算带来极大不便。笔者基于文献[4-7]和能量法对CCBG(CSWs)一次简支超静定结构的约束扭转微分方程进行补充修正，结合三弯矩法,运用该微分方程对某三跨等截面波形钢腹板连续曲线箱梁进行受力性能研究，构建有限元模型检验理论的适用性，并将本文方法与曲杆结构力学法进行分析比较。

1 控制微分方程的建立

1.1 剪力滞引起的梁体应变能

假设CCBG(CSWs)的竖向挠度为ω，竖向剪力引起的剪切变形为θ，则横截面的纵向位移函数μ可表示为[5,7]

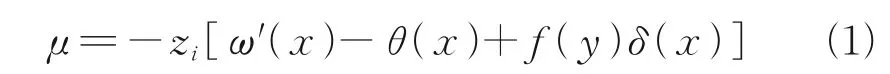
式中：x轴沿桥纵向；y轴沿桥横向；z轴沿桥竖向。

根据式(1)纵向位移函数，可得截面的弹性应变

式中：zi为梁横截面形心距顶底板形心的间距；δ为翼缘板剪切转角的最大差值；Ψ为截面的扭转角；R为曲线半径；ƒ为剪滞翘曲位移函数[5]。

结合文献[6,8-9]，由剪力滞引起的梁体应变能Wq为

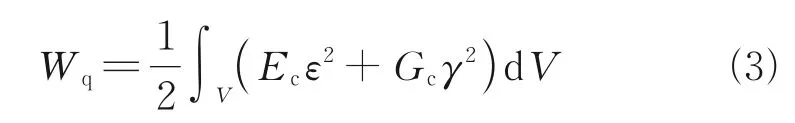
1.2 其他应变能

根据文献[4,10]，约束扭转翘曲应变能Wω为

根据文献[4,7]，腹板剪切应变能Wf为

根据文献[4,10-11]，约束扭转剪切应变能WT为

考虑到畸变引起的变形不参与到CCBG(CSWs)的内力求解，并且畸变引起的变形与上述5种变形相互独立。因此，在对波形钢腹板连续曲线箱梁的内力求解中不考虑畸变产生的影响。

1.3 外荷载势能

外荷载势能W外可表示为

式中：q、m分别为竖向分布荷载和竖向分布扭矩。

1.4 总势能

根据文献[4-5]，结构的总势能可表示为

1.5 补充修正的约束扭转控制微分方程

由最小势能原理可知：弹性体在外力作用下结构实际产生的变形是系统总势能变分为零，即ΔW=0。可推得补充修正的CCBG(CSWs)一次简支超静定结构的控制微分方程为

式中：Ec、Gc分别为混凝土的弹性模量和剪切模量；As为波形钢腹板横截面面积；Au为箱梁翼板剪滞翘曲面积；Iω为广义扇形惯性矩；Iy为箱梁横断面对y轴的惯性矩；I1、I2分别为翼板剪滞翘曲惯性积和翼板剪滞翘曲惯性矩；Id、Iρ分别为箱梁截面抗扭惯性矩和极惯性矩；β为扭转翘曲广义位移；θ为波形钢腹板剪应变；q、m分别为竖向分布荷载和分布扭矩。Ge为波形钢腹板有效剪切模量为波形钢腹板实际剪切模量；a、b、α为波形钢腹板的几何参数[12-14]，如图1所示。

图1 波形钢腹板示意图Fig. 1 Sketch of corrugated steel webs

通过伽辽金法[4,15]对约束扭转控制微分方程求解。假设各未知位移及应变的函数为

荷载q和m可表示为

式中：l为简支波形钢腹板曲线梁跨径分别为竖向荷载系数和竖向扭矩系数。

把式（10）、式（11）代到式（9）中，再利用MatLab进行求解，便可求得各未知变量。进而可求得CCBG(CSWs)一次简支超静定结构任意截面的内力。

2 连续曲线箱梁内力求解

采用多跨连续波形钢腹板曲线箱梁的支座全部为抗扭支座，图2为多跨连续平面曲线梁原结构。为了减少赘余力的个数，将波形钢腹板连续曲线箱梁在各墩墩顶支点处切开，而各墩支座仍维持抗扭简支固定，将多孔的CCBG(CSWs)一次简支超静定结构作为基本结构，见图3。

图2 原结构Fig. 2 Original structure

图3 基本结构Fig. 3 Basic structure

为了使变换后的结构与原结构的变形最终能保持一致，在切分处的梁端变形必须能满足变形协调条件，从而便求出各支点横断面的赘余弯矩。根据力法原理，取一次简支超静定曲线箱梁作为基本体系，且考虑到每个基本结构的单位弯矩只对相邻梁跨的内力有影响，因此，每个典型方程都只包含3个赘余弯矩，所得典型方程为[16]

式中：δii、Δip分别为在单位荷载和已知外荷载作用下基本结构产生的位移，可通过式（13）求得。

进而再通过叠加原理便可计算出各桥跨内所有横断面的内力。从典型方程可以看出，与文献[4]的传统力法相比，采用三弯矩法求解波形钢腹板连续曲线箱梁的内力不但减少了未知荷载的数量，而且每个典型方程的柔度系数都只有3个，大大减少了计算工作量，也保证了计算过程中的准确性。

3 算例分析

3.1 有限元模型

将某三跨等截面波形钢腹板连续曲线箱梁作为算例进行分析。该桥跨径为（35 m+50 m+35 m），中轴线在半径为110 m的圆曲线上。混凝土顶底板为C60混凝土。波形钢腹板为Q345C型钢材，1600型波形。其中，波高22 cm，腹板厚12 mm，直板段宽a=43 cm，斜板段水平宽b=37 cm。箱梁横断面的具体尺寸可见图4。在建模和理论计算时，采用将横截面高度取平均值简化为等高度的截面形式，混凝土顶、底板按照面积相等的原则等效为等厚度的截面，换算可得顶、底厚度皆为t=0.3 m。换算后的截面尺寸如图5所示。

图4 箱梁截面实际尺寸图（单位：cm）Fig. 4 Actual size drawing of box girder section（Unit:cm）

图5 箱梁截面简化尺寸图（单位：cm）Fig. 5 Simplified size drawing of box girder section（Unit:cm）

为了检验方法的适用性，利用Ansys构建算例模型。顶、底板和横隔板选用Solid45号实体单元，其中横隔板只在桥梁两端设置；钢腹板选用Shell93号壳单元。两种单元在连接处使用同一个节点，不管二者间的相对滑移。边界约束条件为：最左端两个 支 点 为ux、uy、uz和roty，其 余 支 点 为ux、uz和roty。建立的模型如图6所示。

图6 波形钢腹板连续曲线箱梁有限元模型Fig. 6 Finite element model of continuous curved box girder with corrugated steel webs

3.2 剪滞效应和剪切变形对CCBG(CSWs)简支结构的影响

取算例的50 m主跨作为CCBG(CSWs)一次简支超静定结构的模型。选用公路-I级车道荷载进行加载。均布荷载为10.5 kN/m，布置于全桥；集中荷载为360 kN，布置于跨中位置处。通过将曲杆结构力学法所求内力数据及微分方程、在忽略剪滞效应和剪切变形的情况下所求内力数据以及微分方程、在考虑剪滞效应和剪切变形的情况下所求内力数据与有限元所求内力数据比较，结果见图7。

从图7（a）可以看出：微分方程在考虑剪滞效应和剪切变形的情况下所求弯矩结果除了在跨中中点处与有限元所求弯矩结果差别较大以外，在整个桥跨内，与另外两种计算方法相比，所求弯矩结果更加接近有限元所求弯矩结果；并且微分方程在忽略剪滞效应和剪切变形的情况下所求弯矩结果与有限元所求弯矩结果差别最大。从图7（b）可以看出：在整个桥跨范围内，除了曲杆结构力学法所求扭矩结果在部分桥段内与有限元所求扭矩结果相差比较明显以外，其余桥段内，三者所求扭矩结果几乎一致。从图7（c）可以看出：在整个桥跨范围内，尽管微分方程在考虑剪滞效应和剪切变形的情况下所求剪力结果与有限元所求剪力结果差值百分比起伏比较大，但二者的剪力结果非常接近，并且3种理论所求剪力结果都与有限元所求剪力结果非常接近。

由图7可知，剪滞效应和剪切变形对CCBG(CSWs)简支结构的弯矩具有比较明显的影响，但对于扭矩和剪力产生的影响比较小；对于CCBG(CSWs)简支结构，运用补充修正的微分方程进行内力求解具有较高的精确度。

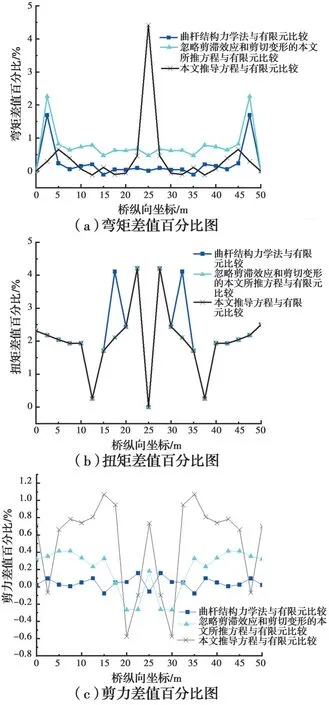
图7 CCBG(CSWs)简支结构内力比较Fig. 7 Comparison of internal forces of CCBG(CSWs) simply supported structures

3.3 剪滞效应和剪切变形对三跨等截面波形钢腹板连续曲线箱梁的影响

选用公路-I级车道荷载进行加载。均布载荷为10.5 kN/m，只布置于中跨；集中载荷为360 kN，布置于中跨跨中。为了检验该方法的适用性，采用该方法和曲杆结构力学法对某波形钢腹板三跨等截面连续曲线箱梁进行内力求解，并采用MatLab编程对理论进行计算，最后将曲杆结构力学法的内力计算结果、该方法的内力计算结果分别与有限元的内力计算结果进行对比分析；忽略剪滞效应和剪切变形影响将，采用该方法所求内力计算结果与有限元所求内力计算结果进行对比分析。所得内力差值百分比见图8。

从图8（a）可以看出：在整个桥跨范围内，与曲杆结构力学法所得弯矩结果相比，该方法所得弯矩结果更加接近于有限元模型所得弯矩结果；从图8（b）、（c）可以看出：在中跨范围内，与该方法所得扭矩和剪力结果相比，曲杆结构力学法所得扭矩和剪力结果更加接近于有限元模型所得扭矩和剪力结果，而在边跨范围内，正好相反。由图8可以看出，在整个桥跨范围内，与曲杆结构力学法所得内力结果相比，该方法所得内力结果更加接近于有限元所得内力结果。说明考虑剪滞效应和剪切变形影响，采用该方法对波形钢腹板连续曲线箱梁的内力求解具有更好的适用性和更高的准确性。

从图8也可以发现：在整个桥跨范围内，忽略剪滞效应和剪切变形的影响，采用该方法所求内力结果与曲杆结构力学法所求内力结果非常接近，表明在进行实际桥梁结构理论受力分析计算时，需要考虑剪力滞和剪切变形引起的结构变化。

图8 三跨波形钢腹板连续曲线箱梁内力比较Fig. 8 Comparison of internal forces of three-span continuous curved box girder with corrugated steel webs

通过以上分析可以发现：考虑剪滞效应和剪切变形的影响，该方法所求简支和三跨波形钢腹板曲线箱梁内力结果都与有限元所求内力结果最为接近；而忽略剪力滞和剪切变形的影响时，该方法所求内力结果与曲杆结构力学法所求内力结果非常接近。以上结论表明：考虑剪滞效应和剪切变形影响，该方法对CCBG(CSWs)内力求解具有更高的精确性和更好的适用性。

4 结论

1）通过分别对比曲杆结构力学法、考虑剪滞效应和剪切变形影响、不考虑剪滞效应和剪切变形影响所求CCBG(CSWs)简支结构内力结果与有限元所求CCBG(CSWs)简支结构内力结果可知：剪滞效应和剪切变形对CCBG(CSWs)简支结构的弯矩具有比较明显的影响，而对于扭矩和剪力的影响比较小。

2）通过对比该方法、曲杆结构力学法与有限元三者所求某三跨等截面波形钢腹板连续曲线箱梁所求内力结果可知：考虑剪滞效应和剪切变形的影响，将推导的CCBG(CSWs)一次简支超静定结构约束扭转微分方程，结合三弯矩法求解波形钢腹板连续曲线箱梁内力具有更好的适用性和准确性。

3）剪力滞效应和剪切变形对CCBG(CSWs)的内力存在着一定的影响，且对于多跨CCBG(CSWs)结构内力的影响更加明显。