桥梁型式对40 m简支梁磁浮车致动力响应的影响

李小珍,胡启凯,王渝文,王党雄

（1. 西南交通大学 土木工程学院，成都 610031；2. 西北工业大学 力学与土木建筑学院，西安 710072）

与传统的轮轨交通相比，磁浮列车通过电磁力悬浮于轨道上方，不与轨道梁相接触，具有高速、舒适、便捷、低耗等优点，其应用前景广阔[1]。中低速磁悬浮列车通过主动悬浮控制产生电磁悬浮力，使磁悬浮列车能够稳定悬浮并平稳运行，其车桥耦合振动问题涉及磁浮列车、悬浮控制系统和轨道梁3个模块之间的相互耦合作用[2]。

在磁浮系统的车桥耦合振动方面，已有学者进行相关研究，Deng等[3]提出了高温超导磁悬浮车—桥耦合系统的6个自由度动力学模型，并模拟了不同条件下的动态响应。Zhao等[4]建立了10个自由度的磁浮列车模型并讨论了随机不规则激励引起的竖向耦合振动特性。文献[5-6]探讨了悬浮间隙在不同跨度和桥梁刚度下的变化规律。Wang等[7]利用通用机械软件对高温超导磁悬浮车—桥耦合系统的动力学性能进行仿真，并对不同速度范围内的高温超导磁浮车—桥耦合系统进行了进一步的设计。Han等[8]讨论了桥梁质量、刚度和阻尼对磁悬浮列车动力性能的影响。Lee等[9]重点研究了运行速度、轨道不平顺、桥跨长度和桥梁阻尼比对悬浮间隙的影响。Milani等[10]基于自适应鲁棒控制系统，研究了具有时滞效应、参数不确定性和外部负载的磁悬浮列车运行的稳定性。Zhou等[11]对轨道不平顺引起的磁悬浮列车振动进行了调查，提出了一种自适应振动控制方案来降低磁悬浮列车的振动。韩霄翰等[12]研究了轨道梁结构对中低速磁浮车—轨耦合振动的影响。

随着桥梁建造技术的提高，在静力技术上，磁浮线路中较大跨度混凝土简支梁已经日趋成熟，设计者可以设计不同型式的简支梁来提高其竖向刚度（如箱型梁上梁、并置单线梁等），但其在磁浮列车作用下的动力性能目前未知，且研究较少。笔者在前人研究的基础上，针对梁轨一体和梁上梁两种40 m混凝土简支梁方案，建立精细的磁浮列车—简支梁系统耦合振动理论模型，深入探讨磁浮列车作用下40 m简支梁的车致动力响应特征，并对不同型式的40 m简支梁对系统耦合振动的影响机理进行剖析。

1 中低速磁浮列车—桥梁的动力相互作用模型

1.1 中低速磁浮车辆的竖向模型

以LMS中低速磁浮列车为研究对象，主要构件包括车体、二系悬挂、悬浮架等，车体通过二系悬挂与悬浮架连接，每节列车有5对悬浮架，每对悬浮架有4对悬浮电磁铁，同时，每个悬浮架上有2个二系悬挂与车体相连，图1为简化的构造示意图。

图1 LMS中低速磁浮列车的简化示意图Fig. 1 Simplified diagram of LMS medium-low speed maglev train

实际磁浮列车结构复杂，数值模型不能完全考虑所有部件和连接，因此，对磁浮列车数值模型采用一些必要的假设：数值模型中考虑了主要部件，包括车体、二系悬挂和悬浮框架，除二系悬挂外，这些组件都假定为刚体；将每个悬浮电磁铁产生的悬浮力简化为集中力；采用线性弹簧阻尼单元对空气弹簧进行建模。

车体考虑竖向（zc）、俯仰（βc）2个自由度，每个悬浮架考虑竖向（Zs）、俯仰（βs）2个自由度，因此，每节列车共计12个自由度。根据图1，作用在车体和悬架上的载荷如图2所示，其中：Fzij(i=1～5，j=1,2)表示第i个悬浮架上第j个弹簧阻尼力；fsin(i=1～5，n=1～4)表示第i个悬浮架上的第n个悬架力；ds为每个悬浮架上二系悬挂的距离；ls为相邻电磁力的间距。

根据达朗贝尔原理，磁悬浮车体的竖向和俯仰运动方程为

式中：Mc和Jc分别为车体的质量和俯仰力矩；lxij(i= 1～5, j= 1,2)为车身质心之间的纵向距离。

悬浮架的竖向和俯仰运动方程为

式中：Ms和Js分别为悬浮架的质量和俯仰力矩。

每个弹簧阻尼力可以表示为

式中：Kz和Cz分别为二系悬挂的竖向刚度和阻尼。则车辆的运动方程可写成

式中：Mv为车辆运动方程的质量矩阵；Cv为阻尼矩阵；Kv为刚度矩阵；Fv为外荷载列向量；Zv为自由度矩阵。

1.2 桥梁系统模型

将轨道结构和桥梁模型视为单个桥梁系统，并使用模态叠加理论[13]进行求解，在外荷载作用下，桥梁的运动微分方程为

式中：m、c、k分别为桥梁的质量矩阵、阻尼矩阵、刚度矩阵；f为作用于桥梁的外荷载（电磁悬浮力）列向量。

利用模态叠加法，桥梁的位移可表示为

式中：φn为桥梁的第n阶振型向量；qn为桥梁的第n阶广义坐标。

将式（8）带入式（7）中，基于振型的正交性，建立桥梁系统模型的解耦微分方程

式中：q̈n、q̇n、qn为桥梁的n阶广义加速度、速度以及位移坐标；ξn为桥梁的第n阶阻尼比；ωn为桥梁的第n阶自振频率；为关于桥梁质量归一化的桥梁各阶振型*

n为经过振型归一化后的广义外荷载。在求解桥梁系统运动微分方程时，只需求出系统的固有频率和作用在桥梁上的广义外荷载。一般情况下，通过有限元软件ANSYS对桥梁体系结构离散化，即可得到各种类型的桥梁体系在任意节点处的自振频率、振型和n阶广义外荷载值。

1.3 PID主动悬浮控制系统模型

中低速磁浮列车通过U形电磁铁和导轨之间的电磁力支撑车体，如图3所示。

图3 电磁铁悬浮模型Fig. 3 Electromagnet suspension model

由电磁理论[14]可知,电磁悬浮力和悬浮间隙的平方成反比，与线圈电流的平方成正比，其计算公式为

开环的电磁悬浮系统不稳定，即使受到很小的外部干扰都会失去平衡。为了实现稳定悬浮，必须进行主动反馈控制。采用PID主动悬浮控制系统模型，基于位移—速度—加速度反馈的PID主动悬浮控制系统的波动电流Δi(t)可以用悬浮间隙波动值Δc(t)、电 磁 铁 的 绝 对 速 度Δx̂̇(t)和 绝 对 加 速 度Δẍ(t)表示，如式（12）所示。

式中：Kp、Kv、Ka分别为位移、速度以及加速度反馈系数。悬浮间隙波动值为实时悬浮间隙与额定悬浮间隙（8 mm）的差值，然而磁铁绝对速度信号Δx̂̇(t)一般不能直接测得，需要使用状态观测器，借鉴文献[14]，状态观测器的表达式定义为

式中：ξ0、ω0分别为系统状态观测器的阻尼和特征频率，Δĉ(t)、Δĉ̇(t)、Δẑ̇(t)、Δẑ̈(t)为在状态观测器里重构的状态观测变量。

通过拉普拉斯变化求得该系统的传递方程为

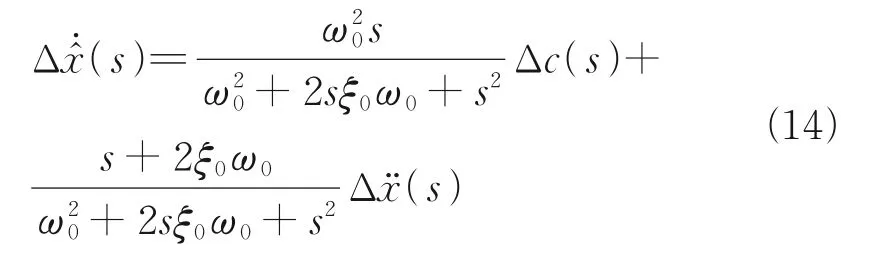
式中：Δx̂̇(s)为状态观测器构造的速度反馈变量；s为拉普拉斯变量。

结合式(11)和式(12)可得控制点处的悬浮力为

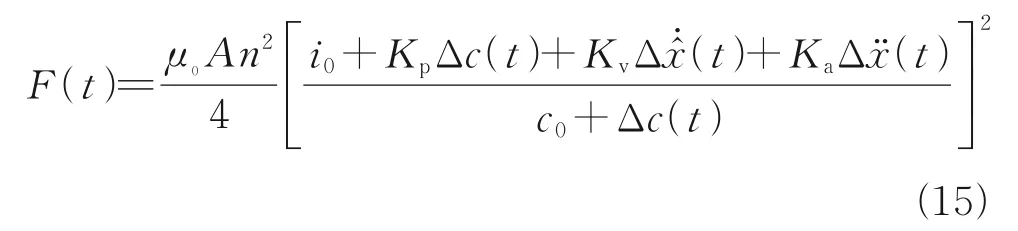
式中：u0为磁导率；i0和c0分别为额定悬浮电流和额定悬浮间隙；A为磁极面积；n为线圈匝数。

通过PID主动悬浮控制，将该悬浮力作用于轨道和磁浮列车的电磁铁之间，可维持悬浮间隙的稳定，悬浮力与车辆和桥梁的运动状态密切相关。

1.4 耦合振动模型求解

不同于传统轮轨，磁悬浮列车在运行过程中没有轮轨接触，但轨道不平顺会对悬浮间隙造成扰动。为稳定悬浮间隙，电磁铁与桥梁间的控制器产生电磁力并作用于列车与桥梁，使二者产生振动，加剧了磁浮间隙波动，因此,磁浮列车与桥梁是一个耦合系统。电磁力作为纽带，将桥梁与车辆的运动联系在一起，与桥梁及车辆的运动状态紧密相关，形成磁浮列车—桥梁耦合运动的状态，如图4所示。

图4 磁浮列车—桥梁耦合振动系统示意图Fig. 4 Diagram of maglev train-bridge coupling vibration system

将式（6）和式（9）结合，可得到磁浮列车—桥梁耦合系统的动力相互作用方程

式（16）是一个非线性时变大系统的动力学方程，在求解系统动力学方程过程中，车辆与桥梁系统的等效刚度在车辆运行过程中发生变化，可采用基于Newmark-ß积分的分离迭代法求解，将桥梁系统的运动方程与车辆分离，再用Newmark积分法逐步求解，具体可见文献[15]。

1.5 耦合振动模型的可靠性验证

基于MATLAB编制磁浮车—桥耦合振动分析程序，联合有限元软件ANSYS提供桥梁结构的计算信息。以长沙磁浮试验中典型的25 m简支梁作为验证对象，图5所示为长沙中低速磁浮列车空载以80 km/h的车速在25 m简支梁上运行时的仿真与实测曲线对比。

由图5可以看出，由于未考虑F轨，25 m简支梁竖向挠度的仿真值刚度较小，挠度较大，但波形相近；简支梁、车辆和悬浮架的动力响应仿真值与实测值均较吻合，证明了所建立磁浮车—桥耦合振动模型的正确性和仿真分析程序的可靠性。

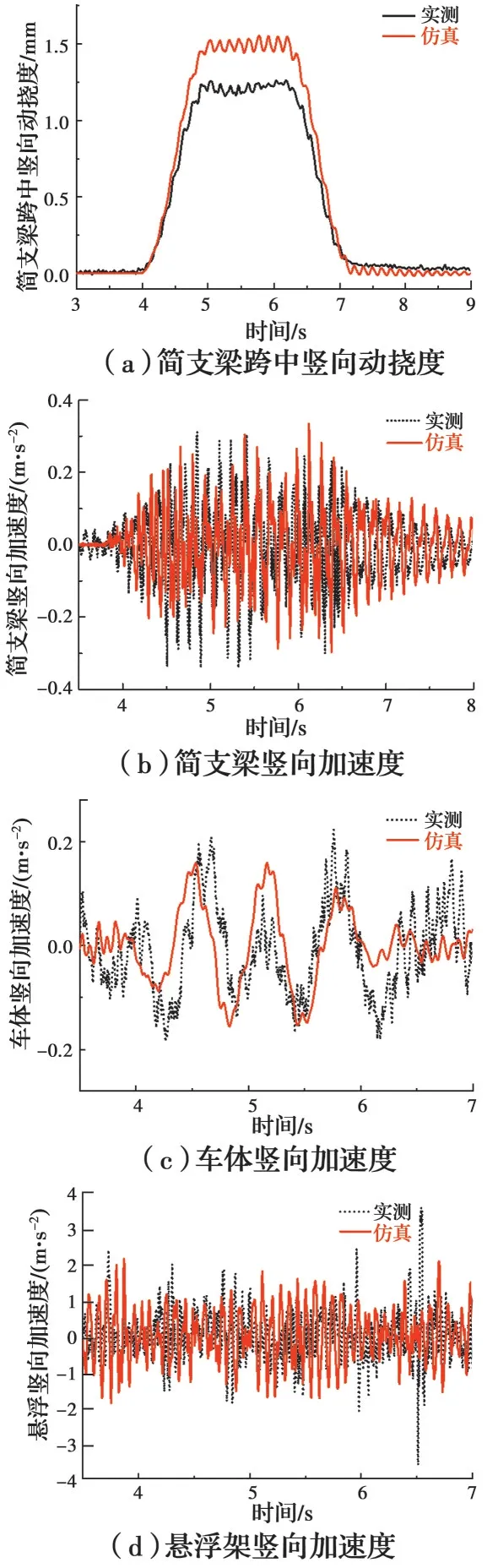
图5 实测与仿真对比图Fig. 5 Comparison diagram of measurement and simulation

2 不同型式40 m简支梁的车致系统动力响应

2.1 方案

采用梁轨一体方案和梁上梁方案两种型式的40 m混凝土简支梁，梁轨一体方案将简支梁和轨道结合成一体，采用并置箱梁，结构构造简单，其板件结构尺寸较小，而梁上梁方案将承轨梁置于简支箱梁之上，采用大箱梁，存在顶板、腹板、翼板和底板等板件，而相比于梁轨一体方案，这些板件尺寸较大，相互间的约束较弱。

2.1.1 梁轨一体方案 简支梁桥跨度40 m，为并置单线箱梁。梁体采用C50混凝土，跨中截面见图6。二期恒载为每线22 kN/m。

图6 梁轨一体方案简支梁跨中截面（单位：cm）Fig.6 Mid span section of simply supported beam in beam rail integration scheme (Unit: cm)

采用通用大型有限元分析软件ANSYS建立40 m简支梁梁轨一体方案动力分析模型，全桥使用板壳单元建模，在简支梁左侧支承处约束所有的平动自由度和绕x轴方向的转动自由度，在右侧支承处约束y轴、z轴方向的平动自由度和绕x轴方向的转动自由度，如图7所示。

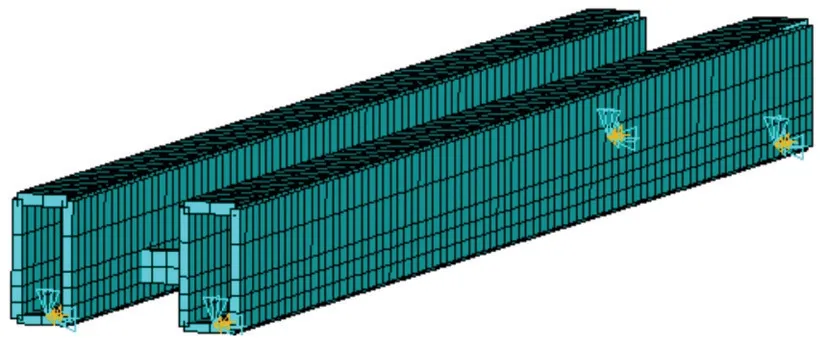
图7 梁轨一体方案简支梁ANSYS有限元模型Fig 7 ANSYS finite element model of simply supported beam in beam rail integration scheme

2.1.2 梁上梁方案 梁上梁跨度40 m，为双线轨道梁。梁体采用C50混凝土，跨中截面见图8。二期恒载采用每线69 kN/m，其中轨道梁的重量为40 kN/m，实际轨道梁为匹配轨道结构，采用短跨布置，其刚度对箱梁整体刚度贡献较小，所以将其作为二期恒载加在简支箱梁上。

图8 梁上梁方案简支梁跨中截面（单位：cm）Fig. 8 Mid span section of simply supported beam in beam on beam scheme (Unit:cm)

同样地，建立40 m简支梁梁上梁方案的动力分析模型，全桥也使用板壳单元建模，在简支梁左侧，两处支承分别约束x轴、y轴、z轴方向和x轴、z轴方向的平动自由度；在右侧，两处支承分别约束y轴、z轴方向和z轴方向的平动自由度，如图9所示。

图9 梁上梁方案简支梁ANSYS有限元模型Fig. 9 ANSYS finite element model of simply supported beam in beam on beam scheme

2.2 模态对比分析

表1分别列出了梁轨一体方案和梁上梁方案下简支梁的自振特性频率分析结果，图10为不同方案中简支梁典型的模态图。由表1可知，梁轨一体方案和梁上梁方案的一阶正对称竖弯和一阶反对称竖弯的频率较为接近，并且梁上梁方案在第15阶模态依然发生整体振动，而梁上梁方案在第6阶模态就开始出现了局部振动，这是由于梁上梁方案的简支梁为大箱梁结构，各个板件均较薄弱，根据文献[16]的研究可知，其较易产生板件的局部振动。

图10 不同方案典型模态图Fig. 10 Typical modal diagrams of different schemes

表1 不同方案自振特性对比Table 1 Comparison of natural vibration characteristics of different schemes

2.3 40 m简支梁的动力响应

在后续分析中，均使中低速磁浮列车在超载的状态下以最大车速120 km/h通过两种不同型式的简支梁，图11、图12为两种型式下简支梁的跨中竖向最大动挠度和加速度的对比图。

从图11可以看出，梁轨一体方案的简支梁竖向动挠度大于梁上梁方案，最大值分别为5.41、2.75 mm，说明在单线行车的情况下梁上梁方案整体刚度更大。从图12的时域图可以看出，梁轨一体方案的桥梁跨中竖向加速度小于梁上梁方案，最大值分别为0.31、0.57 m/s2；从频域图可以看出，梁轨一体方案的桥梁振动主要集中在0～5 Hz，主要为低频振动，优势频率为3.01 Hz。除了整体振动外（一阶竖弯频率为3.70 Hz），梁上梁方案还存在明显的丰富的局部振动模态（主要集中在20～50 Hz），除整体振动外，还表现为高频振动。结合图11、图12可知，梁上梁方案虽然整体刚度较大，但由于在高频段（20～50 Hz）存在较明显的局部振动，从而导致竖向加速度在高频段显著大于梁轨一体方案。综合来看，梁上梁方案的振动加速度仍然大于梁轨一体方案。

图11 简支梁跨中竖向动挠度对比Fig. 11 Comparison of vertical dynamic deflection of simply supported beams in mid span

图12 简支梁跨中竖向加速度对比Fig. 12 Comparison of vertical acceleration of simply supported beams in mid span

2.4 车辆的动力响应

图13、图14为两种简支梁型式下车体的跨中竖向最大动位移和加速度对比图。

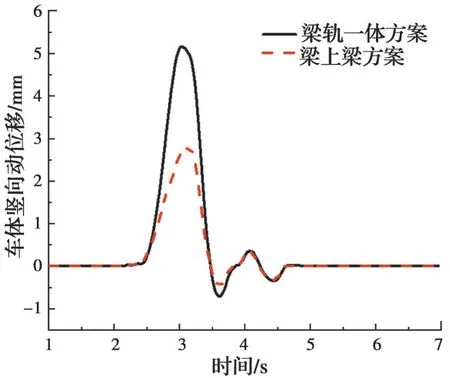
图13 车体竖向动位移对比Fig. 13 Comparison of vertical displacement of car body

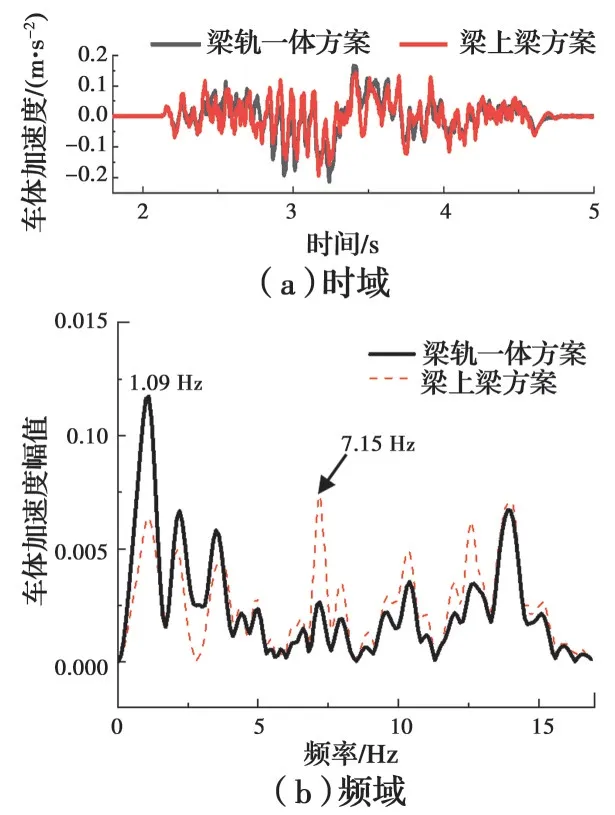
图14 车体竖向加速度对比Fig. 14 Comparison of vertical acceleration of car body

从图13可以看出，梁轨一体方案的车体竖向动位移规律同简支梁竖向动挠度相似，几乎为梁上梁方案的2倍，最大值分别为5.17、2.79 mm。从图14的时域图可以看出，两种方案的车体竖向加速度波动规律和数值均相近，最大值分别为0.22、0.20 m/s2；从频域图可以看出，两种方案下车体的振动主要发生在0～15 Hz，梁轨一体方案的优势频率为1.09 Hz，梁上梁方案的优势频率为7.15 Hz。

2.5 主动控制系统的动力响应

采用基于位移—速度—加速度反馈的PID主动悬浮控制系统来模拟磁浮列车的悬浮控制，图15为两种型式下悬浮间隙和悬浮力的对比图。

图15 悬浮系统的动力响应对比Fig. 15 Comparison of dynamic response of suspension system

由图15（a）可知，悬浮系统通过调节电磁悬浮力，使悬浮电磁铁持续稳定在额定悬浮间隙（8 mm）附近波动，并且波动范围都较小，单幅波动幅值不超过2 mm，总的波动幅值不超过4 mm。这说明磁浮列车平稳运行时电磁悬浮系统能够很好地进行主动控制调节，因此，磁浮车体的动位移与桥梁的动挠度数值基本相等。从图15（b）、（c）可以发现，两种方案的悬浮力和悬浮间隙的波动规律和数值几乎相同，并且悬浮力波动值的优势频率均为11.14 Hz。

悬浮系统的振动和轨道不平顺有关，悬浮系统有自身的优势频率，这是固有的属性，与外界的干扰无关，两个方案的桥梁型式不同，但轨道不平顺相同，结合图15（c）可知，两个方案中悬浮系统的优势频率相同，其动力响应受桥梁型式影响微弱。

2.6 方案对比

由上述分析可知，和梁轨一体方案相比，梁上梁方案的桥梁刚度更大，变形更小；磁浮列车对低频振动较为敏感，仅考虑低频振动时，梁上梁方案的桥梁振动加速度较小，但由于局部振动的影响，总体来看梁轨一体方案的桥梁振动加速度更小；梁轨一体方案是将两个箱梁用一个个横隔板连接，其整体性不如梁上梁方案。笔者研究的是40 m简支梁，在研究更大跨度的简支梁时，梁上梁方案更优。

由文献[17]可知，从经济性角度出发，由于承轨梁不参与结构受力，梁上梁方案材料浪费较多，经济性较差，而梁轨一体方案梁体体量较小；从施工角度出发，梁上梁方案施工较为复杂，施工精度难以保证，而梁轨一体方案受控因素少，施工更为灵活；从后期维修的角度出发，梁上梁方案维护方便，梁轨一体方案维修较为困难。

综合桥梁动力响应、经济性、施工、后期维修等因素，梁轨一体方案更优。

3 不同型式对系统耦合振动影响的机理分析

3.1 简支梁的波长效应影响

磁浮力对简支梁结构的激励频率的定义如式（14）所示。

式中：v为车辆运行速度，m/s；λ为简支梁结构振动波长，m；f为周期性不规则引起的激励频率，即磁浮力对简支梁结构的激励频率，Hz。磁浮列车的运行速度为120 km/h，激励频率和波长的关系如图16所示，由于梁轨一体方案中简支梁的顶板和底板宽度较窄，腹板对顶底板的约束较大，所以，梁轨一体方案在低阶模态中只有整体振动，局部振动只存在于高阶模态，整体振动产生的典型波长为80、40 m（对应表1中的一阶正反对称竖弯）。而梁上梁方案中则存在丰富的局部振动模态，局部振动产生的典型波 长 为40、20、13.33 m（对 应 表1中 的 局 部 振 动模态）。

图16 简支梁振动的典型波长Fig. 16 Typical wave length of simply supported beam vibration

轨道不平顺特性会影响简支梁的频率，磁浮列车对简支梁的影响是周期性的，当简支梁变形为规则正弦波时，简支梁也会产生周期性振动，由于梁上梁方案中存在较多的局部振动，使得简支梁振动的波长减小。由图16可知，激励频率随波长的减小而增大，导致梁上梁方案振动加速度幅值更大，所以，简支梁振动的波长会影响简支梁本身的频谱频率分布特征。

3.2 不同型式的模态影响

由模态对比分析可知，在梁上梁方案中，第6阶及之后的模态都出现了局部振动，从而引起的桥梁结构变形中同时存在整体变形和局部变形，文献[18]指出，中低速磁浮列车中，若考虑F轨的影响，由于其局部振动较为明显，导致轨道—桥梁系统的位移导纳在F轨的局部一阶竖弯存在峰值，说明局部振动对桥梁自身变形影响较大，所以，模态的不同会对桥梁变形产生影响；结合图12的频域图可知，由于局部振动发生的频率较高，和梁轨一体方案相比，梁上梁方案简支梁的振动主要发生在较高的频率；结合图14的频域图可知，桥梁的局部振动会反作用于车体。文献[19]指出，在考虑F轨的局部振动后，车体的竖向振动加速度增大，所以局部振动同时也会影响车体的动力响应，由于局部振动主要存在于高频中，从而导致梁上梁方案中车体振动的优势频率大于梁轨一体方案。

4 结论

建立了考虑主动悬浮控制的中低速磁浮列车—桥梁系统竖向耦合振动模型，针对两种不同型式的简支梁，将所建模型进行对比，分析两种不同方案下40 m简支梁中低速磁浮车致系统的动力响应，进而探讨不同桥梁型式对系统耦合振动的影响机理，得到以下结论：

1）相较于梁上梁方案，梁轨一体方案的桥梁竖向动挠度更大，加速度更小，桥梁振动的优势频率分别为3.01、3.70 Hz；梁轨一体方案的车体竖向动挠度大于梁上梁方案，两种方案的车体竖向加速度相近，车体振动的优势频率分别为1.09、7.15 Hz；综合桥梁动力响应、经济性等因素，梁轨一体方案更优。

2）悬浮系统有自身的优势频率，其动力响应与外界干扰无关，受桥梁型式影响微弱，本文中悬浮系统的优势频率为11.14 Hz。

3）梁上梁方案中简支梁存在丰富的高频局部振动模态，故存在较密集的短波振动效应，增大了桥梁变形和桥梁与车体的振动优势频率。

4）由于桥梁型式不同，简支梁变形的波长和模态不同，从而通过波长效应、局部振动等影响磁浮列车—轨道—桥梁系统的耦合振动。