以槽电势为分析单元的大型发电机定子接地故障定位方法

乔 健，尹项根，王义凯，谭力铭，徐 雯，李 伟

（1. 华中科技大学 强电磁工程与新技术国家重点实验室，湖北 武汉 430074；2. 国网新源控股有限公司抽水蓄能技术经济研究院，北京 100053）

0 引言

大型发电机作为主力支撑电源，其安全运行是保障电力系统可靠供电的基础。定子绕组的单相接地故障（定子绕组与铁芯间的绝缘破坏）是发电机最常见的一种故障［1］。随着发电机单机容量的增大，相应的单相接地电流也随之增大。若不采取措施，则会危及定子铁芯，易演变为匝间或相间短路故障［2］。目前大型发电机通常配置双频式100%定子接地保护（基波零序电压+3 次谐波电压保护）和注入式定子接地保护［3-4］（下文简称注入式保护）。在定子接地保护动作发信号后，应解开发电机与外部的连接，利用保护装置的录波数据实现定子绕组的接地故障定位，以减少故障排除工作量和缩短停机检修时间。

目前，已有多种基于不同保护装置的录波数据的定子接地故障定位方法。文献［5］提出一种仅使用基频测量信息的故障定位方法，该方法利用机端三相基波电压和基频零序电压计算接地过渡电阻，进而推算出故障位置。文献［6］利用回路电流法构建故障后的3 次谐波等效电路，基于中性点和机端处测量的3 次谐波电压求解故障位置和过渡电阻。文献［7］提出一种基于注入式保护的定子接地故障定位方法，该方法利用注入式设备的低频信息测量过渡电阻，进而实现故障定位。然而，上述方法忽略了定子绕组电势分布的相位特征［8］，计算结果存在理论误差。文献［9］以线圈匝电势为单元分析故障分支的电势分布特征，利用注入式设备测量过渡电阻，最终通过查表法定位故障所在线圈。文献［10］利用基波电势的分布特征计算各线圈末端故障时的基频零序电压轨迹圆弧，通过与故障录波数据进行对比判断故障所在线圈，在高阻故障时可能存在多解，需借助注入式设备辅助判断。文献［11］基于绕组电势的相位特征分析首次提出了绕组电势分布的公式表示，从而实现了故障位置的数值求解。但上述方法均是以线圈匝电势为单元分析绕组的电势分布。对于短距绕组的机组，忽略了线圈两边槽电势的相位差异。此外，线圈是由2 个跨度较远的槽导体串联组成的。对于故障检修，将故障定位结果精确到槽编号更有实际意义。因此，文献［12］提出了一种能够将故障位置精确至槽编号的故障定位方法，但该方法需在发电机内部安装测量装置，实现较为困难。

为此，本文提出一种以槽电势为分析单元的大型发电机定子单相接地故障定位方法。发生定子单相接地故障后，基于绕组连接顺序在线辨识基波槽电势和3次谐波槽电势，进而建立绕组基波和3次谐波电势分布的精确解析表达。对于配备了注入式保护的发电机，利用注入式设备测量过渡电阻，基于发电机的基频零序等值电路构造故障评价指标。对于未配备注入式保护的发电机，通过引入3 次谐波测量值构造不含过渡电阻的故障评价指标。最后，在故障相各分支上设置多个虚拟参考点，计算各虚拟参考点的故障评价指标，将计算值最小的虚拟参考点视为故障位置并将其所在槽编号发送给检修部门。利用在PSCAD 中搭建的准分布参数模型验证了本文所提方法不受故障位置和过渡电阻的影响，能够满足实际工程的需要。

1 以槽电势为分析单元的绕组电势分析方法

大型汽轮机组和核电机组由于转速较高，多为隐极式结构。以某核电机组为例，该机组采用双层叠绕组的绕线形式，其定子槽数为48，极对数p为2，极距τ为12，定子每相分支数为2，槽距电角度为15°，定子的基波槽电势相量图见附录A 图A1。图中：数字表示槽编号；U表示槽内上层边导体；L表示槽内下层边导体。例如，1U 表示槽编号1 中上层边导体。该发电机每个分支由2 个极相组串联组成，具体地，A1 分支（A 相第一分支）的连接顺序见附录A 图A2。图中：节距为10，是短距绕组形式；O为中性点；H为A1分支的中点（2个极相组的连接处）；每个极相组由4 个线圈串联组成，相邻线圈的匝电势相差15°，构成2 个60°相带分布，见附录A 图A3；F1和F2是2个可能发生的单相接地故障，分别位于2个极相组上。

由线圈匝电势组成的极相组电势分布近似为60°相带的圆弧。因此，文献［13-15］基于该相位特征提出了一种绕组电势的公式解析法。当故障位置位于中性点侧的极相组上时，以故障F1为例，故障绕组（故障点至中性点的绕组）的基波电势E(α1)为：

式中：α1为绕组OF1与绕组OA1的长度比值；EOA1为A1 分支的合成基波电势；EOF1为故障F1所在位置至中性点的绕组电势。

当故障位于机端侧的极相组上时，以故障F2为例，故障绕组的基波电势E(α2)为：

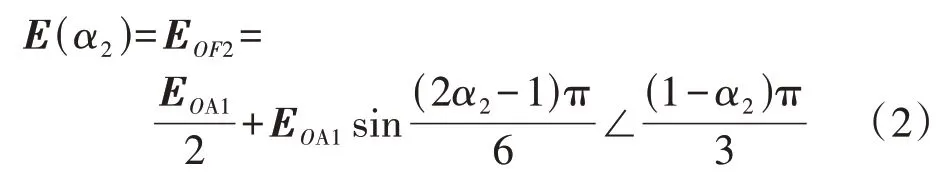
式中：α2为绕组OF2与绕组OA1的长度比值；EOF2为故障F2所在位置至中性点的绕组电势。

由于短距绕组具有端接连线较短、成本较低的优势，大型发电机组普遍采用短距的绕线形式。该绕线形式下，线圈两边槽导体的感应电势存在相位差异。实际的绕组电势分布应以槽电势为单元进行分析，见附录A 图A4。对比图A3、A4 可以发现，短距绕组的机组的实际绕组电势分布与圆弧分布存在一定差异。为更直观地展示该差异，采用故障绕组在该分支绕组中的占比α表示故障位置，令α由0变化至1（从中性点到机端），以线圈匝电势和槽电势为分析单元的分析方法得到的故障绕组的基波电势E(α)的幅值和相位变化情况如图1 所示。图中：α=0和α=1分别表示中性点和机端。由图可见，2种分析方法得到的E(α)幅值几乎相等，在各匝线圈的中点存在少许差异；但E(α)相位的差异较大，尤其在靠近中性点侧发生定子接地故障时，相位差异超过20°，可能导致故障定位结果出现较大误差。因此，对于短距绕组的机组应以槽电势为单元进行分析计算，不能直接套用式（1）、（2）计算绕组电势分布。

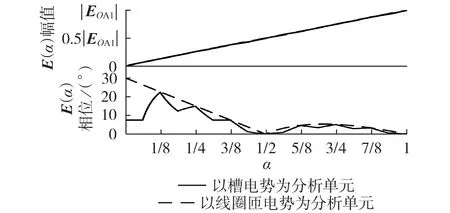
图1 不同故障位置下E(α)的幅值和相位Fig.1 Amplitude and phase of E(α) with different values of α

发电机转速恒定时，可认为所有槽导体的感应电势幅值相等。普遍地，假设定子S相（S=A，B，C）某分支的绕组共由i匝线圈串联组成，其连接顺序为：（x1U，x2L）→（x3U，x4L）→…→（x2i-1U，x2iL）。其中，x1—x2i为槽编号。槽电势的相位见图A1，分别记为βx1—βx2i，则有：

式中：j=1，2，…，2i；EO和ES分别为在分支的中性点和机端处测量得到的基波电势；EX为基波槽电势，EX的相位是槽电势的参考相位与测量电势的参考相位的夹角。因此，可对基波槽电势进行在线辨识，如式（4）所示。

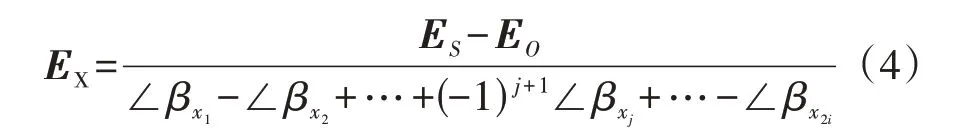
由于以槽电势为分析单元得到的绕组电势分布特征复杂，故障绕组的基波电势E(α)无法如式（1）、（2）那样用一个简单的解析式表达，但可以根据绕组连接顺序以槽导体为单元进行分段，构造分段函数解析式为：

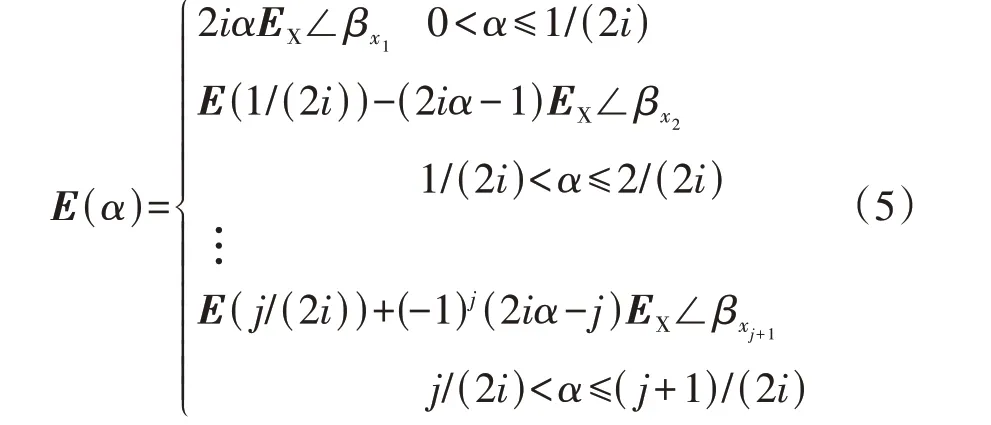
式中：j=0，1，…，2i-1。则E(α)是被分为2i段的分段函数。

2 定子接地故障定位方法

2.1 配备注入式保护

定子接地故障的基频零序等效电路如图2 所示［6］。图中：Cg为定子绕组的每相对地电容；Cz为机端外部等效的每相对地电容；C∑为总体的等效对地电容；RN为发电机的中性点接地电阻一次值；Zk为接地变压器短路阻抗一次值［10］；Rk为短路电阻；Lk为短路电感；Rf为定子接地故障的过渡电阻。根据基尔霍夫电流定律可得：

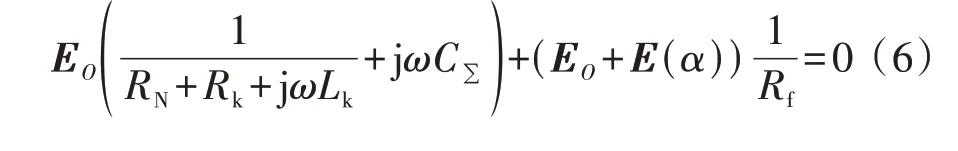
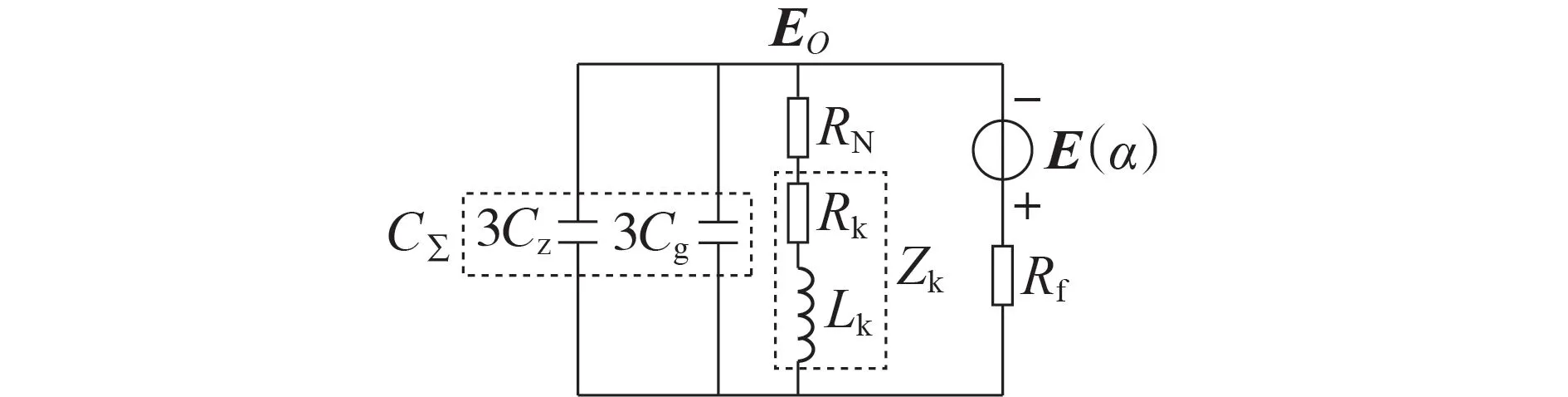
图2 基频零序等效电路Fig.2 Fundamental frequency zero-sequence equivalent circuit

大型发电机为实现定子接地故障的双重化保护，通常会配置100%定子接地保护和注入式保护。注入式保护能够测量Rf［16］，若故障定位程序能够获取Rf的测量值，则式（6）中仅含有E(α)这1 个未知量。联立式（5）、（6）可对α进行数值求解。然而，式（5）是一个多分段的非线性复数函数，求解过程困难，计算耗时较长，直接进行数值求解不可取。

因此，为了简化求解计算量，基于式（6）构造故障评价指标f(E(α))如式（7）所示。

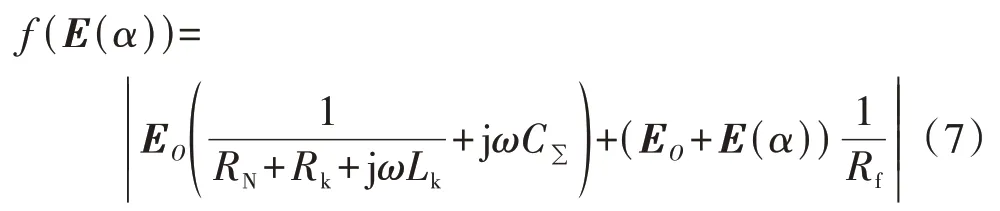
由于不同位置的E(α)是唯一的，只有真实故障点的故障评价指标f(E(α)) 为0，而其他位置的f(E(α))必定不为0，且距离真实故障点越远，对应的f(E(α))越大。考虑到故障检修时是对定子槽内的整根导体进行排查，将故障定位结果精确至槽编号就能满足工程需要，无需得到α的数值解。因此，在每根槽导体上设置3 个虚拟参考点Ri，分别位于槽导体的1/6 处、1/2 处和5/6 处，即相邻虚拟参考点相差1/3个槽导体长度，见附录A图A5。

根据式（5）可计算每个虚拟参考点对应的基波电势E(Ri)。进一步地，利用式（7）计算各虚拟参考点对应的f(E(Ri))并互相对比，将f(E(Ri))计算值最小的虚拟参考点视为故障参考点，进而确定故障所在槽编号，该求解方式本质上是穷举法，无需考虑求解约束条件。以图A5中的虚拟参考点R4为例，若f(E(R4))的计算值最小，则认为定子接地故障位于定子11槽中。

2.2 未配备注入式保护

对于未配备注入式保护或配备了注入式保护但无法获取过渡电阻测量值的发电机，由于式（7）中存在E(α)和Rf这2 个未知量，2.1 节所提方法不再适用。考虑到发电机运行时定子绕组存在较大的3次谐波电势，可结合3次谐波信息进行定子接地故障定位。

类似于基波电势的分析，以3 次谐波槽电势为分析单元可得到定子绕组的3 次谐波电势分布见附录A图A6。由于中性点处和机端处的3次谐波电势E3-O和E3-S是实时测量值，因此，可实时在线辨识3次谐波槽电势E3-X。在不同的运行工况下能够自适应地计算当前时刻的3次谐波槽电势，类似于式（4）有：

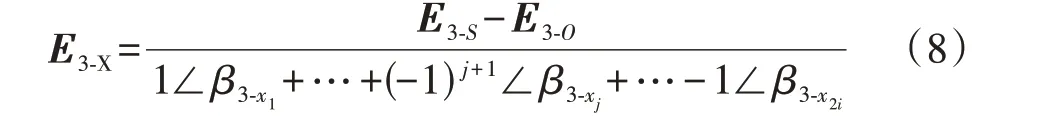
式中：j=1，2，…，2i；β3-xj=3βxj。同理，故障绕组的3次谐波电势E3(α)的解析式为：

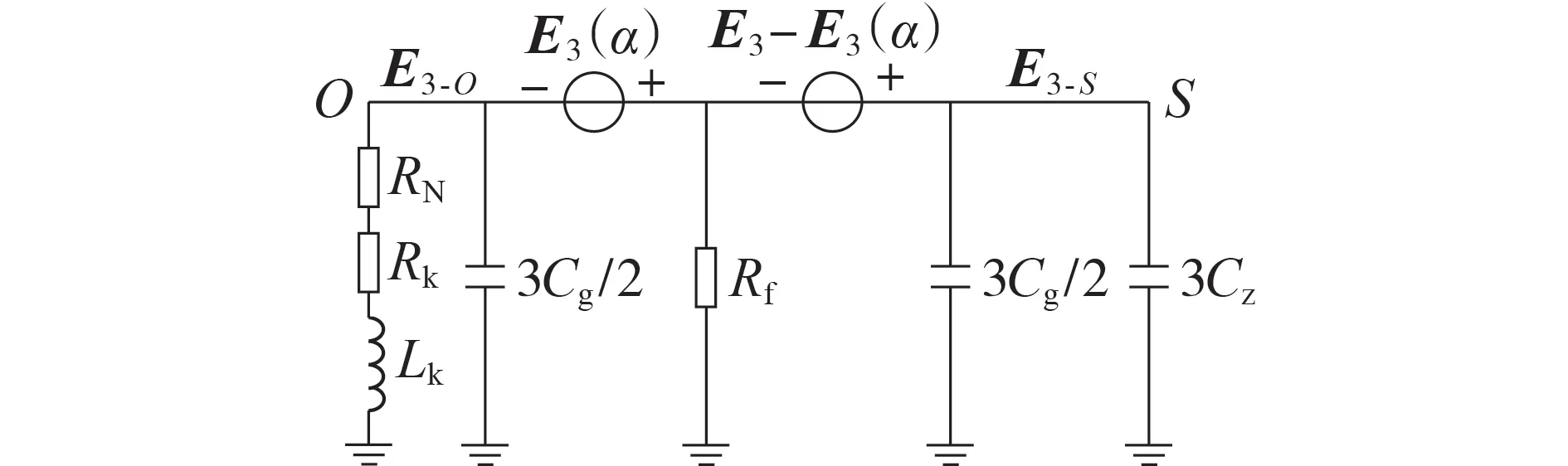
图3 3次谐波等效电路Fig.3 Third harmonic equivalent circuit

联立式（6）和式（10）可得：

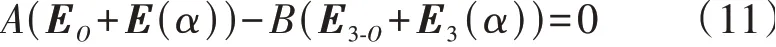
式中：A和B不含有未知量，可由测量值得到，具体如式（12）所示。

式（11）中仅含有E(α)和E3(α)这2个未知量，可构造不含过渡电阻Rf的故障评价指标f(E(α)，E3(α))，如式（13）所示。

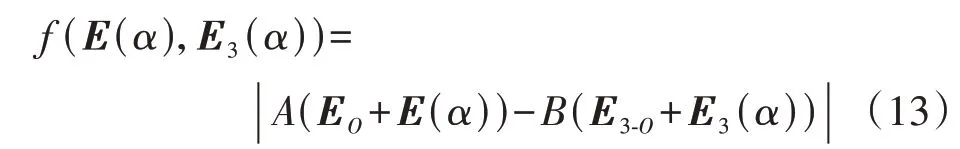
基于式（5）和式（9）可分别计算每个虚拟参考点对应的基波电势E(Ri)和3 次谐波电势E3(Ri)。利用式（13）计算各虚拟参考点对应的f(E(Ri)，E3(Ri))并互相对比，将故障评价指标计算值最小的虚拟参考点视为故障参考点，进而确定故障所在槽编号。

2.3 故障定位流程

本文所提的定子接地故障定位方法的实现流程如图4 所示。对于中性点经高阻接地的发电机，可直接根据故障相电压最低［16］判断故障相。因此，只需在故障相的各分支上设置虚拟参考点，而无需在所有分支上设置虚拟参考点。

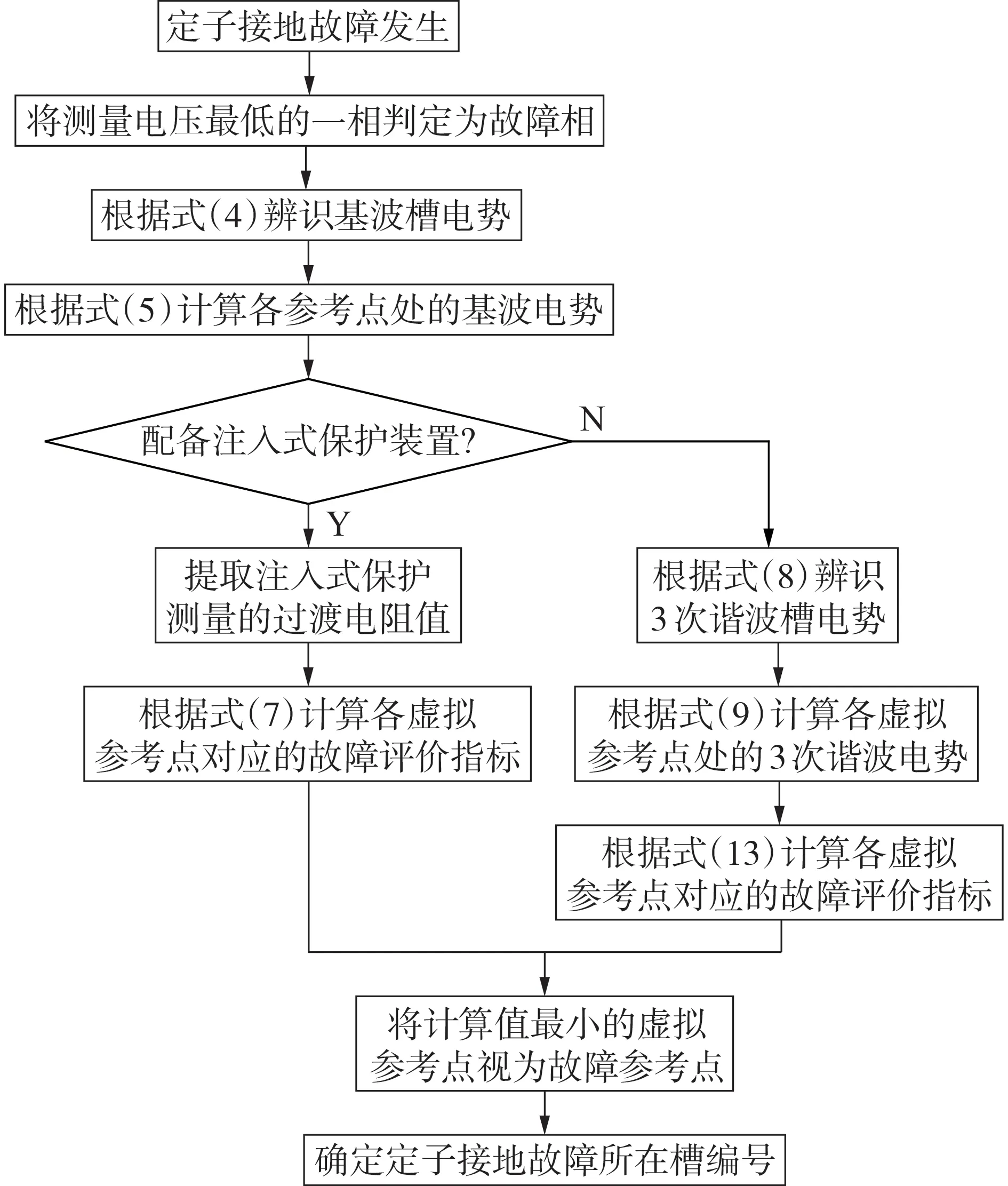
图4 本文所提故障定位方法的实现流程图Fig.4 Flowchart of proposed fault location method

3 仿真分析与验证

3.1 仿真模型

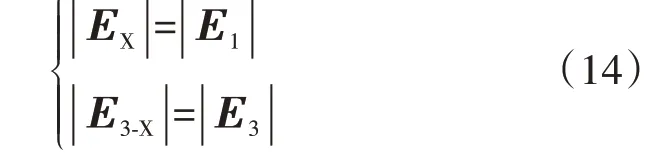
式中：E1和E3分别为实际的基波槽电势和3 次谐波槽电势。

考虑到实际的故障位置可能发生在线圈导体上的任意位置，为了仿真这种情况，在仿真模型中将故障位置所在的单元电路拆分成两部分，并根据故障位置的占比确定这两部分的电气参数，见附录A图A8。

仍以上述核电机组为例，该机组的基本参数如附录A 表A1 所示。由于各分支均由8 匝线圈组成，1 个分支上设置48 个虚拟参考点。该机组A1 分支由中性点到机端的绕组连接顺序为：（1U，11L）→（2U，12L）→（3U，13L）→（4U，14L）→（25U，35L）→（26U，36L）→（27U，37L）→（28U，38L）。

在A1 分支上的6 个位置设置定子单相接地故障，具体如下：f1为第1 匝线圈的下层边导体11L 的中点，即故障位置为虚拟参考点R5；f2为第3 匝线圈的下层边导体12L 的末端1/6 处，即故障位置为虚拟参考点R12；f3为第4匝线圈的上层边导体4U的首端1/6 处，即故障位置为虚拟参考点R19；f4为第5 匝线圈的下层边导体35L 的首端1/3 处，即故障位置为虚拟参考点R28和R29的中点；f5为第6匝线圈的下层边导体36L 的中点，即故障位置为虚拟参考点R35；f6为第8 匝线圈的上层边导体28U 的首端1/4 处，即故障位置介于虚拟参考点R43和R44之间且更靠近虚拟参考点R43。

根据式（4），利用故障前一周期的录波数据对基波槽电势大小进行在线辨识。基波槽电势的实际大小为936.204 1 V，辨识结果为936.361 0 V，相对误差为0.0168%。

3.2 配备注入式保护时故障定位方法的性能分析

当f1—f6处发生过渡电阻为50 Ω 的定子接地故障时，A 相电压最低，被判断为故障相。计算A1分支和A2 分支上所有虚拟参考点的故障评价指标f(E(α))，A1 和A2 分支各有1 个f(E(α))计算值最小的虚拟参考点，而实际的故障位置一定是二者中f(E(α))计算值更小的虚拟参考点。为定量化展示不同分支的区分度，各故障情况下两分支上f(E(α))计算值最小的虚拟参考点及其f(E(α))见表1。表中：Rmin为f(E(α))计算值最小的虚拟参考点；fmin为对应的f(E(α))计算值最小值。由表可见，不同分支的f(E(α))计算值最小值的区分度至少为1 个数量级，不会出现故障分支误判的情况，故障定位结果见附录A 图A9 和表2。可以发现：在不同故障位置下本文所提方法的故障定位结果误差均不超过1 个虚拟参考点间距，能够将故障位置精确到槽编号；当故障恰好位于虚拟参考点上时，该虚拟参考点的故障评价指标最小，f(E(α))几乎为0；当故障位于2个虚拟参考点之间时，更靠近真实故障的虚拟参考点的故障评价指标最小，其f(E(α))略微增大，但仍接近于0。

2019年中国家电市场的预期仍然十分严峻。首先，整个市场环境并没有明显的改善迹象。我国经济持续步入平稳期，2019年的经济发展未见任何明显提振因素。预期2019年经济持续放缓，房地产市场持续下行。而随着城镇化进行的不断推进，城镇化建设也已经放缓，这些因素都将影响家电产品的购买需求。此外，股市的低迷，以及物价的提升，也令很多消费者的购买欲望降温。当然还有中美贸易战的影响，加大了企业的出口压力，或将引起部分企业出口转内销，加大国内市场的竞争压力。整体而言，2019年的外部市场环境趋于恶劣。

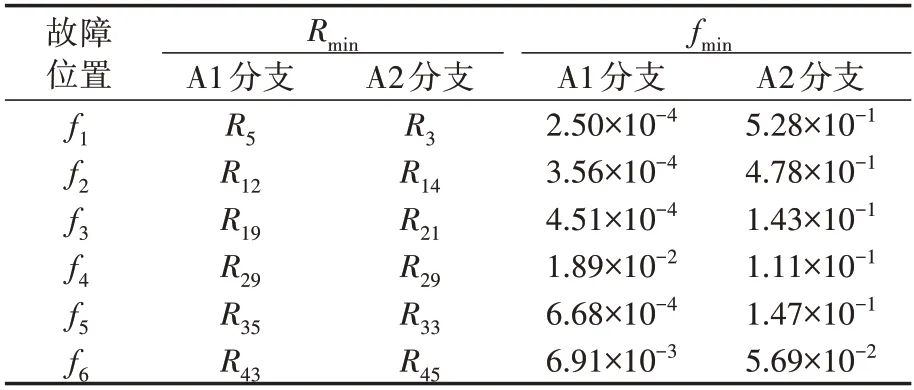
表1 不同分支的f(E(α))区分度Table 1 Differentiation of f(E(α)) between different branches

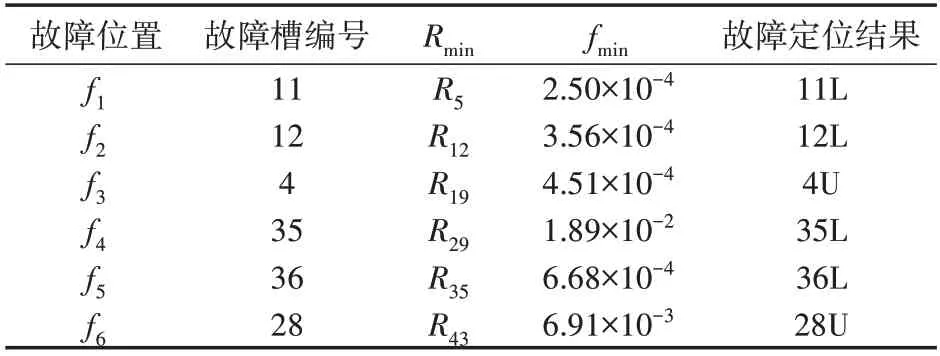
表2 配备注入式保护时，不同故障位置下的故障定位结果Table 2 Fault location results under different fault positions when injection protection is equipped

为了验证本文所提方法在不同过渡电阻下的性能，假设启动判据能够动作，对过渡电阻为100 Ω、1 kΩ、5 kΩ 和10 kΩ 这4 种情况分别进行验证。计算故障分支A1 上的所有虚拟参考点的故障评价指标，故障定位结果见附录A 图A10。可以发现，当过渡电阻的测量值准确无误时，本文所提方法的性能不受过渡电阻变化的影响，故障定位误差不超过1个虚拟参考点间隔（1/3个槽导体长度），具有较高的定位精度。

在实际工程中，基于注入式设备的过渡电阻测量值存在一定的误差，试验结果表明测量误差与接地过渡电阻呈线性相关，随着过渡电阻阻值的增大，相对误差由负到正增大。但在一定的阻值范围内（0～10 kΩ），该相对误差可控制在±5%之内［20-21］。以f2和f5处发生故障为例，当实际过渡电阻为50 Ω时，对过渡电阻测量值分别施加-5%和-10%的测量误差；当实际过渡电阻为10 kΩ 时，对过渡电阻测量值分别施加5%和10%的测量误差。计算故障分支A1上的所有虚拟参考点的故障评价指标，故障定位结果见附录A图A11和表3。可以发现：当过渡电阻较小且存在较大测量误差时，本文所提方法仍能准确定位故障位置；当过渡电阻较大且存在较大测量误差时，本文所提方法存在一定的故障定位误差，但故障定位误差不超过2 个虚拟参考点间隔（2/3 个槽导体长度）。因此，对故障定位结果按绕线顺序两侧临近的槽导体一同进行故障排查一定能准确找到故障点。

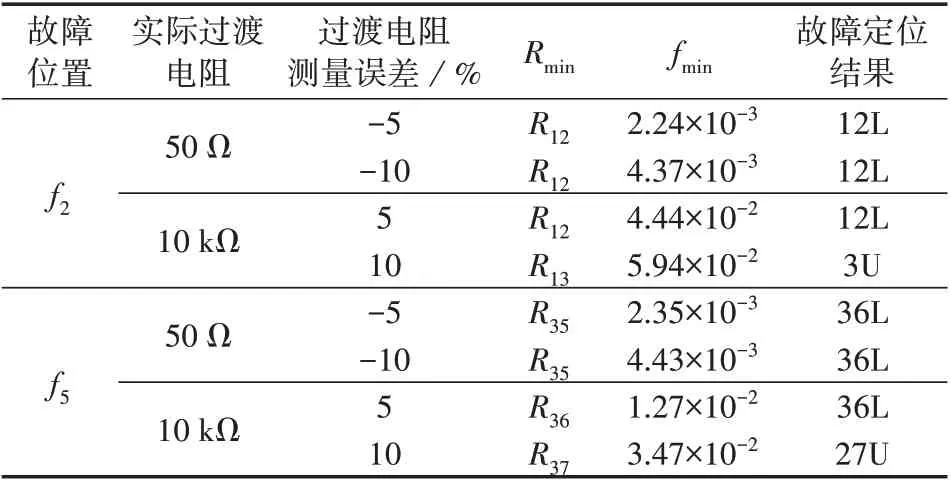
表3 过渡电阻存在测量误差时的故障定位结果Table 3 Fault location results of transition resistance with measurement error

3.3 未配备注入式保护时故障定位方法的性能分析

对于未配备注入式保护或无法获取注入式保护的过渡电阻测量值的发电机，根据式（8），利用故障前一周期的录波数据对3 次谐波槽电势进行在线辨识。3次谐波槽电势的实际大小为312.0680 V，辨识结果为309.2826 V，相对误差为-0.89%。

假设f1—f6处发生过渡电阻为50 Ω 的故障，计算A1、A2 分支上所有虚拟参考点的故障评价指标f(E(α)，E3(α))，A1、A2 分支上f(E(α)，E3(α))最小的虚拟参考点以及f(E(α)，E3(α))的计算值见表4。表中：R′min为f(E(α)，E3(α))计算值最小的虚拟参考点；f′min为对应的f(E(α)，E3(α))计算值最小值。由表可见，不同分支的f(E(α)，E3(α))计算值最小值的区分度至少为1 个数量级，不会出现故障分支误判的情况。故障定位结果见附录A 图A12 和表5，可见本文方法的故障定位结果误差均不超过1个虚拟参考点间距，能够将故障位置精确到槽编号。对比表2、5 可以发现，表5 中f(E(α)，E3(α))的计算结果整体较大。这一方面是因为式（7）和式（13）中评价指标的量纲不同，另一方面是因为3 次谐波槽电势的辨识结果存在更大的误差。但图A12中所有虚拟参考点的故障评价指标整体变大，因此不影响故障参考点的准确判断。

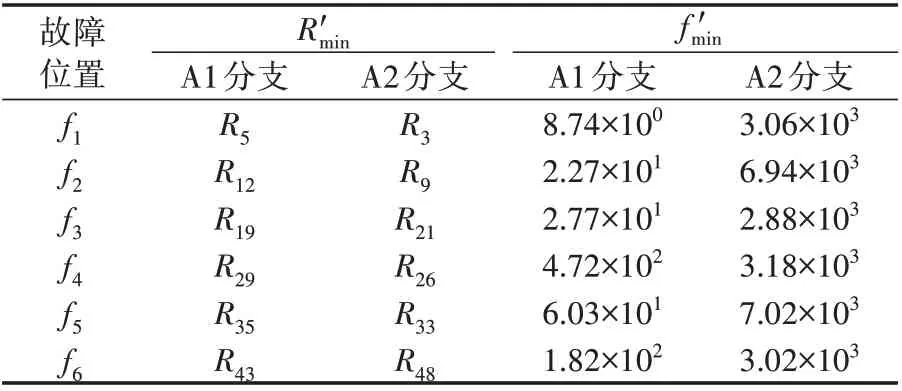
表4 不同分支的f(E(α))，E3(α))区分度Table 4 Differentiation of f(E(α))，E3(α))between different branches

表5 未配备注入式保护时，不同故障位置下的故障定位结果Table 5 Fault location results under different fault positions when injection protection is not equipped

以f1、f3、f4和f6处发生故障为例，若启动判据能够动作，对过渡电阻为5 kΩ 和10 kΩ 这2 种情况分别进行验证。A1分支上各虚拟参考点的f(E(α)，E3(α))计算结果如附录A图A13和表6所示。可见，随着过渡电阻的增大，虚拟参考点的f(E(α)，E3(α))整体变小，故障参考点与非故障参考点的差异性不再明显，本文所提方法的性能逐渐变差。当过渡电阻为5 kΩ 时，不同故障位置的定位误差均不超过3个虚拟参考点间隔（半匝线圈），能够满足应用要求。当过渡电阻达到10 kΩ时，f1、f3和f4处发生故障时，本文所提方法的故障定位误差均不超过3 个虚拟参考点间隔。但f6处发生故障时，本文所提方法将故障位置误判为36L，与实际故障位置相差7个虚拟参考点间隔（1.17 匝线圈长度）。考虑到过渡电阻达10 kΩ 的定子接地故障发生频率较低，且1.17 匝线圈的故障定位误差仍对故障排查有指示作用。因此，当启动判据动作后，本文所提方法在定子经高阻接地故障下仍具有一定的工程应用价值，且对于过渡电阻小于5 kΩ的定子接地故障具有高可靠性。

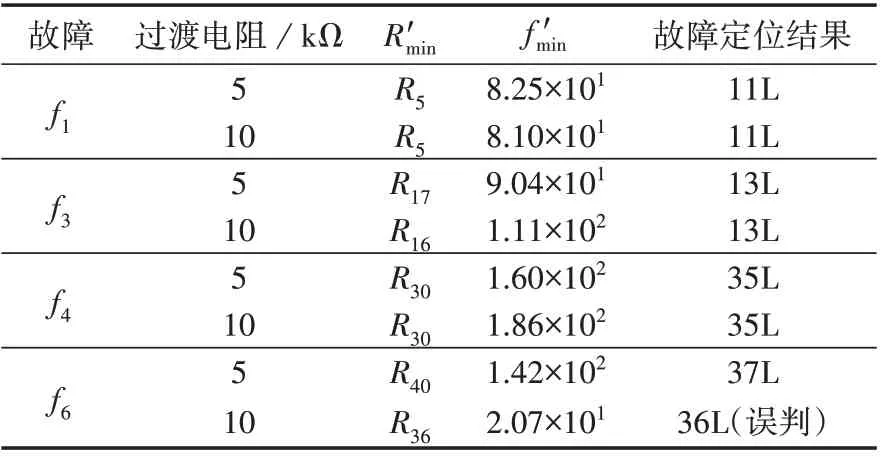
表6 未配备注入式保护时，不同过渡电阻下的故障定位结果Table 6 Location results under different transition resistances when injection protection is not equipped

考虑到发电机机端和中性点处的3 次谐波电压受运行工况影响变化范围较大［22-23］，应考虑机端3次谐波电压E3-S和中性点3 次谐波电压E3-O存在测量误差时本文所提方法的工作性能。对E3-S和E3-O施加-3%～3%的测量误差，3 次谐波槽电势的辨识结果见附录A 表A2。以f3和f4处发生故障为例，假设故障过渡电阻为5 kΩ，计算故障分支A1上的所有虚拟参考点的f(E(α)，E3(α))，故障定位结果见附录A图A14。可以发现，此时本文所提方法的最大定位误差不超过4个虚拟参考点间隔（不超过1匝线圈），说明本文所提方法在3 次谐波电压存在少量测量误差时，其故障定位结果仍具有一定的指示性。但能够预见，若测量误差进一步增大，本文所提方法可能将不再适用。

4 结论

精确的大型发电机定子接地故障定位方法能够有效减少故障排除工作量和停机检修时间，具有显著的经济效益。本文提出一种以槽电势为分析单元的大型发电机定子单相接地故障定位方法，并得出以下结论。

1）提出以槽电势为单元分析定子绕组的电势分布，该分析方法不对绕组电势分布进行任何简化，能够适应短距绕组形式的大型发电机。

2）针对配备注入式保护的发电机，基于注入式保护过渡电阻测量值构造故障评价指标。在故障相上布置多个虚拟参考点，计算各虚拟参考点的故障评价指标，将计算值最小的虚拟参考点视为故障参考点。该方法具有较高的故障定位精度，且对于注入式保护的过渡电阻测量误差具有鲁棒性。

3）针对未配备注入式保护的发电机，提出结合3 次谐波测量值构造不含过渡电阻的故障评价指标，并计算故障相所有虚拟参考点的评价指标，进而确定故障参考点和故障所在槽编号。该方法在3 次谐波电压存在少量测量误差时仍然适用。

附录见本刊网络版（http：//www.epae.cn）。