基于改进贝叶斯网络的风电机组动态可靠性评估

符 杨，苗育植，黄玲玲，刘璐洁，魏书荣，张智伟

（1. 上海电力大学 电气工程学院，上海 200090；2. 上海东海风力发电有限公司，上海 200433）

0 引言

风力发电作为一种技术成熟、应用广泛的新能源发电形式，已经成为我国实现“30·60”双碳战略目标的重要途径之一。截至2020 年底，我国风电总装机容量已达到2.8×108kW，占电源总装机容量的12.8%，风电发电量占全年总发电量的比例也达到了6.12%。风能已逐渐成为一种影响电网电力电量平衡的重要能源形式［1］。开展风电机组实时、动态的可靠性评估，对实现风电场降本增效具有重要意义。

近年来，国内外专家学者针对风电机组／风电场的可靠性评估开展了广泛而深入的研究。在可靠性数据统计方面：文献［2-3］对不同风电机组的故障率、故障停运时间以及不同部件的故障分布等进行统计与分析；文献［4］进一步从状态评估与故障特征提取的角度进行分析，为后续运维决策提供了数据基础。在风电机组的可靠性建模方面，文献［5-6］针对外界环境中风速、温度及机组自身参数的变化对风电机组中叶片和齿轮箱等重要部件可靠性的影响进行建模与分析。在可靠性评估方法方面，故障树法、贝叶斯网络模型等常被应用于可靠性分析的相关性模型中［7］。

上述关于风电机组可靠性的研究，较少考虑风电机组个体实时运行数据在其可靠性评估中的影响和价值。事实上，目前已经能够获得智能化风电机组的振动、温度、声发射、应力、润滑油参数等非电气量信息［8］，以及电压、电流、功率等电气量信息［9］。根据风电机组不同部件的材料、结构、运行特点等，按照不同类型、精度的状态信息对风电机组健康状态进行分析与评估，这些状态信息表现出明显的“多元异质”特点。文献［10］较为全面地梳理和总结了当前常用的风电机组及其关键部件的状态监测与健康诊断技术。风电机组的数据采集与监视控制SCADA（Supervisory Control And Data Acquisition）系统及状态监测系统CMS（Condition Monitoring System）可获取较为全面的机组实时运行状态数据，但是这些“多元异质”特性的数据也给机组的可靠性评估带来了困难。

贝叶斯网络模型由于具有能较好地表示变量的不确定性及变量间的相关性等优点，在基于实时数据的设备可靠性评估中得到了较为广泛的应用［11-12］。文献［13］提出一种基于贝叶斯优化的风电机组发电机故障预警方法，验证了贝叶斯模型的泛化性能。上述研究大多基于某种电气量和非电气量信息，缺乏对“多元异质”状态信息的同质化处理，且传统的贝叶斯方法在推理过程中简化了贝叶斯网络条件，通常缺乏状态信息-故障-部件间的相关性分析，这会导致推理效果不理想，对可靠性评估的结果造成不确定性影响。

针对上述问题，本文提出一种基于改进贝叶斯网络的风电机组动态可靠性评估方法，即根据在风电机组运行过程中收集到的关于其随机行为（或状态劣化情况）的新信息或新知识，对风电机组的可靠性函数进行实时更新［14］。为了清晰阐述改进贝叶斯网络的构建过程与动态可靠性评估方法，本文以风电机组的一个关键部件为例进行说明。算例分析结果表明，所提方法不仅可以有效地基于“多元异质”实时状态信息对机组可靠性进行定量评估，而且可以结合贝叶斯网络的拓扑结构更加全面地描述部件不同故障与各种状态信息间的耦合特性，推导出部件各种状态信息对不同类型、不同等级故障的敏感程度，从而有助于梳理出风电机组不同故障及其典型关键病症信息。

1 研究思路与框架

本文提出的基于改进贝叶斯网络的风电机组动态可靠性评估方法主要包含改进贝叶斯网络的构建与动态可靠性评估2个部分。

首先，针对传统贝叶斯分析方法未能充分考虑实时状态信息“多元异质”的特点、部件与状态信息间的耦合关联关系等问题，提出一种融合故障树分析FTA（Fault Tree Analysis）方法、云模型CM（Cloud Model）与无标度网络的改进贝叶斯网络。针对风电机组故障事件建立故障树模型，以此构建风电机组的基于FTA的可靠性贝叶斯网络FR-BN（FTA based Reliability-Bayesian Network）；针对状态监测信息“多元异质”的特性，构建风电机组状态信息云模型，将FR-BN 转化为更易于诊断与描述动态过程中变量复杂关系的单纯可靠性贝叶斯网络pR-BN（pure Reliability-Bayesian Network）；针对贝叶斯网络中多变量之间的耦合关系造成可靠性评估准确性受限的问题，建立无标度网络［15］，定量分析多变量之间的耦合关系对可靠性分析的影响。

然后，构建动态贝叶斯推理过程与可靠性分析方法。具体而言：在上述改进贝叶斯网络的基础上，引入动态性的迭代更新时刻来构建并优化参数学习与监测信息更新过程；基于无标度网络进行节点变量的耦合分析，并利用加权形式对推理过程中的状态监测信息更新环节进一步优化，在提高动态可靠性评估准确性的同时，实现对状态信息关联特性的表达。基于贝叶斯网络的动态可靠性评估流程图见附录A图A1。

2 改进贝叶斯网络的建模

2.1 基于FTA建立可靠性贝叶斯网络

FTA 具有可以定性推理复杂系统初始失效及事件的影响、建模简单等优势，在可靠性分析领域应用广泛［16］。本文将FTA 的定性演绎推理分析融入贝叶斯网络，构建FR-BN。

这里以风电机组的一个关键部件为例说明FR-BN 的构建过程。首先，根据对该部件的故障分析建立该部件的故障树模型，主要包含顶层事件、中间事件与基本事件3 个部分：顶层事件E为该部件的故障状态；中间事件u为该部件的故障子节点的集合，u=｛u1，u2，…，uN｝，其中ui（i=1，2，…，N）为第i种故障类型，N为该部件故障类型总数；基本事件v为反映该部件病症根节点的集合，v=｛v1，v2，…，vn｝，其中vi（i=1，2，…，n）为第i种病症，n为可能反映该部件病症的总数。部件故障树层间的逻辑关系为：顶层事件E代表该部件的故障状态，中间事件u可以被某种或多种基本事件v中的病症表征。由此，可以得到风电机组关键部件的故障树，如图1 所示，图中q、p、k均为正整数且1＜q＜p＜k＜n。然后，将该风电机组关键部件的故障树进行贝叶斯网络转化，从而得到该部件的FR-BN，见附录A图A2。

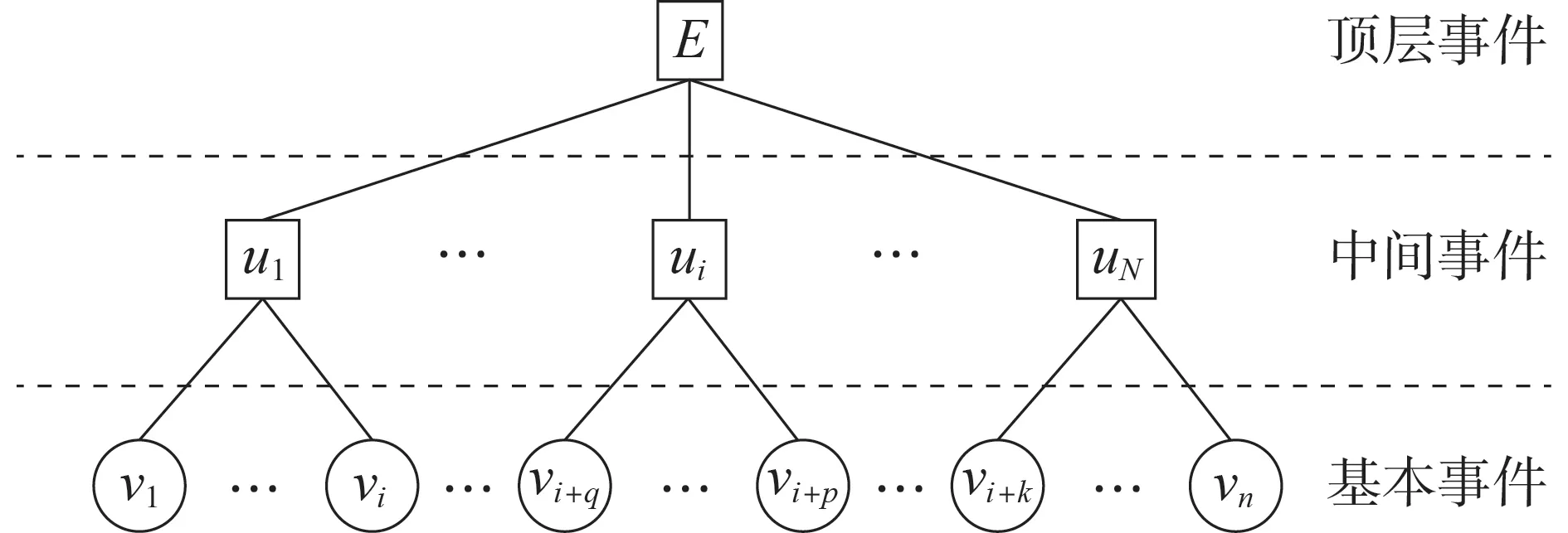
图1 风电机组关键部件的故障树Fig.1 Fault tree of key component of wind turbine

2.2 基于云模型的FR-BN变量区间分析

FR-BN 中存在大量病症根节点vi及其对应的部件监测信息节点mi。本文利用云模型区间分析的优势来解决状态监测信息“多元异质”特性所带来的状态区间多样性问题，将FR-BN改进为pR-BN，具体步骤如下。

步骤1：定义随机变量ξ=｛ξ1，ξ2，…，ξn｝，确定初始化状态空间，其中ξi（i=1，2，…，n）为第i个随机变量，表征FR-BN中的监测信息节点mi的状态。

步骤2：定义区间离散化后的状态数为y，则可将随机变量的定性论域D划分为y个子域［D1，D2，…，Dy］，每个变量将产生对应的云模型［C1，C2，…，Cy］，其中Di（i=1，2，…，y）为第i个子域，表征状态变量所对应的状态区间，Ci（i=1，2，…，y）为第i个区间云模型，表征Di所对应的状态区间。

步骤3：针对多变量多区间的状态信息云模型，利用云发生器，由各个区间云模型的数字特征参数Ci［xExi，xEni，xHei］（i=1，2，…，y）可以产生得到符合各区间要求的变量值，其中xExi、xEni、xHei分别为Ci的期望、熵及超熵。

步骤4：将云模型参数代入隶属度函数进行区间分析，可以得到不同离散状态的隶属度μi（i=1，2，…，N）。

2.3 基于无标度网络的pR-BN耦合关系分析

贡献度矩阵方法［15］可以有效地定量分析系统多元参数之间的贡献度关系，本文通过构建风电机组pR-BN 各节点间的贡献度矩阵Lc，实现对pR-BN 中各节点间耦合关系的量化，即：

式中：lij（i，j=1，2，…，S）为节点j对节点i的重要性贡献比例，其值越大，表示节点间的关联性越强，S为pR-BN中的节点总数。

为了将贡献度矩阵Lc从描述节点间的关系推广至描述节点对整体特征的影响（如描述状态信息vi、vj（i≠j）对部件节点E（反映部件状态）的共同影响），本文引入无标度网络的概念［15］，对pR-BN 进行进一步优化。

首先，基于pR-BN 构建图G=（U，V，E）的网络拓扑。图G共有S个节点，其中包含n个病症根节点、N个故障子节点和1 个部件节点，网络图见附录A 图A3。图中：u1、u2、…、uN构成所有故障子节点集合U；v1、v2、…、vn构成所有病症根节点集合V；w（i，j）为节点i与节点j间的局部权重。

根据图A3的网络拓扑结构，可以得到部件节点E与故障子节点ui间的关联矩阵，记为AN×N=（aE(ij)）N×N，其可表示不同故障原因与部件之间的关系，矩阵元素为：

将故障子节点ui与病症根节点vj间的关联矩阵记为Bn×n=（bij）n×n，其可表示不同故障病症与不同故障之间的关系，矩阵元素为：

根据图论理论［15］，可以得到任意节点i的邻接度Q(i)，表示与节点i相连的所有邻居节点的度之和，如式（4）所示。

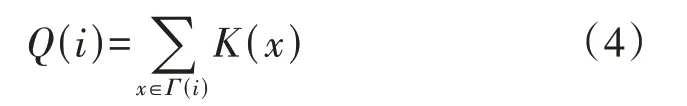
式中：Γ(i)为节点i的邻居节点集合；K(x)为节点x的度。

为更好地反映节点在整个网络中的拓扑关系，引入节点i的次邻接度。由式（4）结合2 类关联矩阵AN×N、Bn×n，可得到节点i的次邻接度I(i)，如式（5）所示。当节点i为部件节点E时，I(i)表示在风电机组状态信息v能表征故障u的情况下，故障u导致部件E运行异常或发生故障的程度。

为明确节点间相互影响的耦合关系，定义一种状态结构洞［15］来研究相邻节点间的贡献关系，结构洞数量能够在一定程度上反映网络结构的稳定性，数量越多，网络结构越稳定［17］。定义约束系数作为测量指标，以衡量网络中大量的病症根节点vi及故障子节点ui在形成结构洞时受到相邻节点的约束情况。节点i的状态结构洞指标Li为节点i的约束系数与网络中所有节点约束系数的比值，即：

结合式（2）、（3）、（6），可以得到节点j对节点i的重要性贡献比例，即：

通过结合贡献度矩阵Lc与关联矩阵，可以计算修正后的节点局部权重矩阵w(i，j)，如式（11）所示，可将其应用于后续贝叶斯推理中的加权优化。

基于此，拓展到整个网络结构，可以得到：

式中：W为综合表征节点局部特征与全局信息的权重关系矩阵；W1Z和W2Z分别为病症根节点与故障子节点所对应的自身初始权重。结合式（10）与式（12），可以得到敏感度矩阵，如式（13）所示。

式中：Hc为敏感度矩阵，其元素值大小可用来描述风电机组各部件的各种状态信息对不同类型、不同等级故障的敏感程度。

上述为风电机组单部件的贝叶斯网络建模思路与方法，根据贝叶斯网络的拓扑结构特点可以将多个部件的贝叶斯网络进行拓展和整合，从而构成更加复杂的多部件系统的贝叶斯网络模型。

3 基于改进贝叶斯网络的推理与可靠性分析

传统的静态贝叶斯分析根据先验概率和相关条件来推导节点（部件）后验概率，即：

式中：P(H)、P(A)分别为事件H和事件A的先验概率；P(H)|A为已知事件A发生后事件H发生的条件概率，即事件H的后验概率。通过对先验概率和后验概率的迭代更新，可以获得可靠性的动态变化过程。

为了描述风电机组动态可靠性评估中的动态贝叶斯推理过程，这里定义贝叶斯推导过程中第k个迭代更新时刻为Tk。考虑到待输入动态贝叶斯网络推理的数据主要来自于风电机组实时数据系统——SCADA 系统，为了满足不同时间精度的计算需要，更好地利用状态监测信息进行动态推理，Tk可以取值为SCADA 系统数据采样时刻的整数倍。基于动态贝叶斯推理的风电机组动态可靠性评估流程图见附录A图A4。

3.1 参数学习

参数学习是指网络的先验概率、条件概率及后验概率的学习。

1）先验概率。

先验概率一般由经验或数据统计得到。通常可以假设风电机组主要部件的故障率数据服从指数分布［16］，因此，通过监测信息节点mi获取的关于某种故障病症vi反映部件可能发生不同严重程度故障（一般故障、中度故障及严重故障）的概率可以表示为：

式中：P{·}表示概率；λd为部件故障率，d=2 表示发生一般故障，d=3 表示发生中度故障，d=4 表示发生严重故障；t为部件运行时间。基于上述部件不同严重程度的故障，结合状态空间的多变量概率分析，可将定性论域D分为4个子域，分别对应节点的4种风险状态，以突出监测信息“多元异质”的特点，即D1表示极低风险状态区间，D2表示中风险状态区间，D3表示高风险状态区间，D4表示极高风险状态区间。由于风电机组当下的风险状态概率之和为1，因此有：

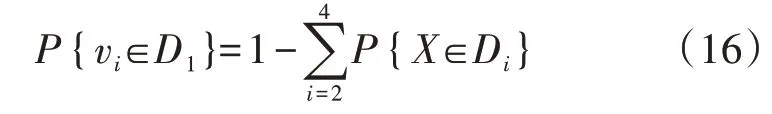
2）条件概率及后验概率。

引入迭代更新时刻Tk后，由式（14）结合式（15）和式（16）可得到式（17），其表示在已知病症vj的条件下，能反映发生故障ui时部件E的状态隶属于各个风险状态区间的概率。

类似地，可以将式（18）中的P(uki，vk1，vk2，…，vkj)作为先验概率，结合式（14）推导Tk时刻的部件风险概率，如式（19）所示，化简后如式（20）所示。

式中：P(Ek，uki)为Tk时刻在故障子节点ui的影响下，部件E发生故障位于各风险区间的概率，Ek为Tk时刻部件E的取值。根据式（20）可以得到已知部件故障ui的条件下，部件E隶属于各个风险状态区间的概率。

3.2 监测信息更新

监测信息更新是指随着更新时刻Tk的推移，不断获取新的状态监测信息，从而不断更新各个节点的状态概率。

1）实时状态概率。

若将Tk+1时刻病症根节点新的监测信息记为ec，将该时刻故障子节点新的监测信息记为eF，则可将实时监测的信息作为更新依据，结合式（18）和式（20），变量之间的相关概率可以表示为：

2）状态转移概率。

结合本文的云模型设备状态健康区间，这里的状态转移概率是指设备状态由隶属于一个健康区间向隶属于另一个区间转移的概率，可以表示为：

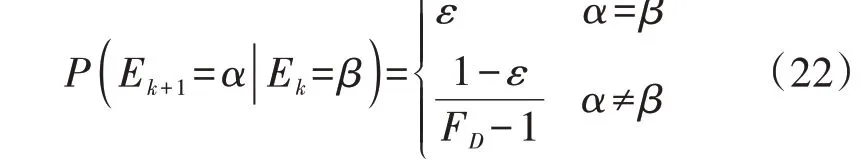
式中：α、β分别为Tk和Tk+1时刻设备所属的风险状态类型；ε为Tk和Tk+1时刻设备状态属于相同风险状态区间的概率；FD为云模型中定性论域D的子域个数。

3.3 耦合分析

由于pR-BN 节点变量之间相互独立，因此，式（21）中病症根节点的依赖性可以展开为：

3.4 可靠性分析

由上述分析过程可见，式（26）确定了部件在Tk时刻隶属于给定健康状态（D1、D2、D3、D4）的概率，因此，结合式（22）、（24）、（26），可以得到式（27）。

式中：R(Tk+1)为基于Tk时刻的状态信息更新的Tk+1时刻的部件可靠度；Ei(Tk)为在Tk时刻第i个部件节点E的取值；V(Tk)为Tk时刻故障子节点的状态取值；ΔT=Tk+1-Tk。

4 算例分析

这里以我国某近海风电场的多年运行数据为基础，对齿轮箱这一关键部件的可靠性评估过程进行分析。相关的运行与监测数据取自该风电场的SCADA系统。

4.1 pR-BN的建立

根据风电机组齿轮箱运行与故障特征规律［18-19］，选择几种典型关键状态参数来构建故障树：顶层事件E为齿轮箱状态；中间事件u=｛u1，u2，u3｝，其中u1为齿轮箱齿弯曲故障，u2为齿轮箱齿面胶合故障，u3为轴承过热故障；基本事件v=｛v1，v2，v3，v4，v5，v6｝，其中v1为冲击载荷位移，v2为子轴承状态，v3为齿间润滑效果，v4为润滑油温度，v5为轴承润滑效果，v6为传感器状态。

以状态变量v1、v4为例，运用云模型对其进行变量多区间离散化处理，计算结果见附录A表A1。

4.2 动态贝叶斯推理

根据式（15）、（16）获得部件节点的先验概率，结合式（18）、（20），可以计算得到故障子节点及部件节点在初始时刻T1的后验概率，分别见附录A 表A2和表A3。

由表A2 可以看出，在T1时刻，u1、u2、u3隶属于D1的概率分别为0.699 75、0.448 42、0.499 80，这说明齿轮箱部件在T1时刻不易发生这3种类型故障。表A3中齿轮箱部件E的状态概率为0.48265，这说明该部件在T1时刻大概率属于极低风险状态区间。

根据式（10）计算得到部件与状态信息之间的贡献度矩阵为：

由式（29）可以看出：矩阵Lc对角线元素为1，对角线以上与以下对应元素大多呈现倒数规律；元素Lc（1，4）、Lc（4，8）最大，均为5/2，元素Lc（2，9）最小，为1/6，这说明节点1 与节点4、节点4 与节点8 之间的耦合关联性最强，节点2与节点9之间的耦合关联最弱。具体而言：风电机组齿轮箱部件的正常运行与否与轴承是否过热密切相关，且润滑油温度v4最能反映轴承过热故障u3；轴承润滑效果v5与齿轮箱齿弯曲故障u1之间的关联性最弱。该结果与文献［20］采用深度变分自编码网络方法得到的结果一致，证明了本文所提分析方法的正确性和有效性。

4.3 模型有效性分析

截取风电机组齿轮箱四五年运行期间的4 个典型时段数据，共9 000 个更新时刻。4 个典型时段分别为：TA为新设备时段，TB为长时间正常运行后的磨损时段，TC为突发某一故障之后的故障时段，TD为更换维护后的修复时段。同一时段内的相邻更新时刻的时间间隔ΔT=Tk+1-Tk=240 min。

经过上文的动态贝叶斯推理和计算，得到齿轮箱部件在上述给定的各个运行时段的状态风险概率变化结果图，见附录A 图A5。由图可以看出：计算得到的健康状态区间的隶属概率正确地反映了部件可靠性的变化。具体而言：在TA时段，P｛E∈D1｝逐渐增大，并且从T982时刻开始P｛E∈D1｝逐渐接近于1，这说明经过一段时间的磨合运行，新安装齿轮箱的工况性能趋于稳定；在TB时段，从T3001时刻开始P｛E∈D1｝逐渐降低，这说明经长时间运行后，齿轮箱可能发生故障的概率升高；在TC时段，P｛E∈D1｝急剧降低，在TD时段，P｛E∈D1｝逐渐升高，均符合故障发生前与新部件更换后设备可靠性的变化特征。这表明本文提出的基于改进贝叶斯网络的状态区间隶属概率能够定性反映齿轮箱部件可靠性的变化趋势。

为了体现改进贝叶斯网络定量分析动态可靠性的作用，对比本文方法与文献［21］中传统蒙特卡罗方法在TB、TC、TD时段的可靠性分析结果。蒙特卡罗方法可靠性分析流程见附录A 图A6。2 种计算方法的结果对比如图2所示（图中可靠度R(Tk)为标幺值）。

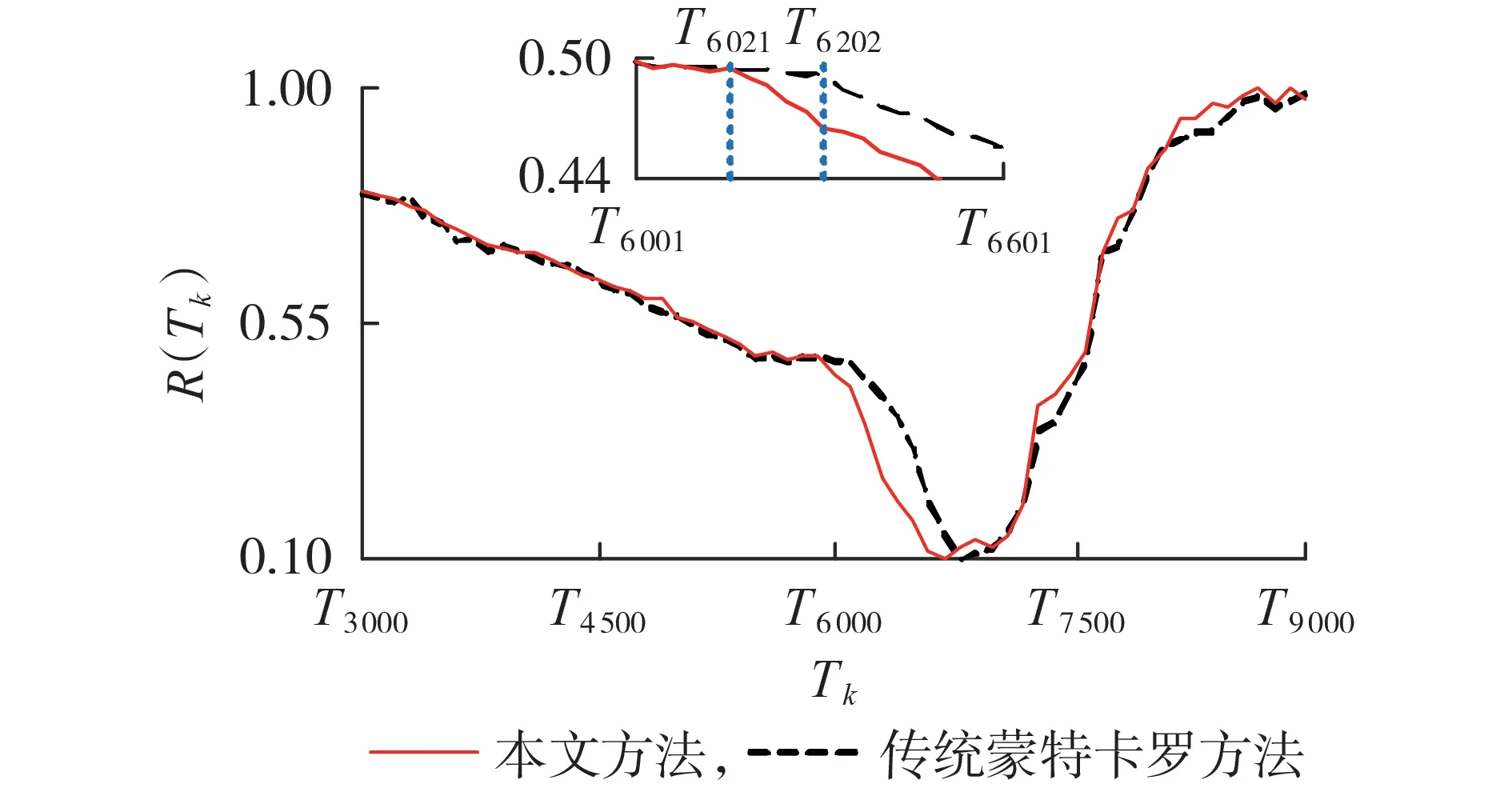
图2 本文方法与传统蒙特卡罗方法对比Fig.2 Comparison between proposed method and traditional Monte Carlo method

由图2 可知：本文方法较好地贴合了传统蒙特卡罗方法的结果，最大误差为6.323%，验证了本文方法的有效性；对于发生于T6001时刻的突发故障，本文方法能够在T6021时刻反映突发故障后可靠度快速下降，而传统蒙特卡罗方法则需在T6202时刻才能反映突发故障后可靠度的变化，相比于本文方法滞后了181 个更新时刻，即本文方法能够提前1 086 h 表征突发故障后可靠度的变化，这表明本文方法能够准确描述可靠度的变化趋势，为后续状态运维决策提供更加充分的决策时间。

4.4 模型优越性分析

为了进一步体现改进贝叶斯网络的优越性，探究网络中部件、状态间拓扑结构对可靠性评估准确性的影响，这里将加权无标度网络方法和未加权传统蒙特卡罗方法［21］进行对比，关联性分析结果如图3 所示（图中耦合系数为标幺值），其中不同耦合系数下的结果对比图见附录A图A7。

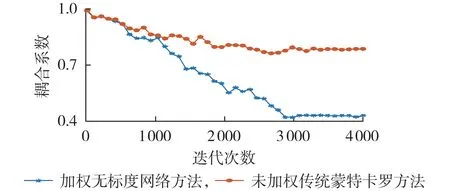
图3 2种方法拓扑结构耦合关联性对比Fig.3 Comparison of topological structure coupling correlation between two methods

由图A7 可以看出：当迭代次数达3 000 时，利用加权无标度网络方法得到的耦合系数下降到0.4189，而利用未加权传统蒙特卡罗方法得到的耦合系数下降到0.8570，这充分描述了部件、状态间的复杂耦合关系；通过将耦合系数的数值降低到0.49，可以得到更加贴合基准的风险概率变化趋势，这说明耦合系数反映了网络中节点间相互影响的大小，通过改变节点的连接关系来适当降低耦合系数，有利于提高可靠性分析时的准确性。

在上述分析的基础上，进一步借助加权无标度网络方法对敏感度矩阵Hc进行分析。选取3 种故障（u1—u3）、6种状态信息（v1—v6），对比不同状态监测信息对不同类型故障的故障敏感度（标幺值），如图4所示。

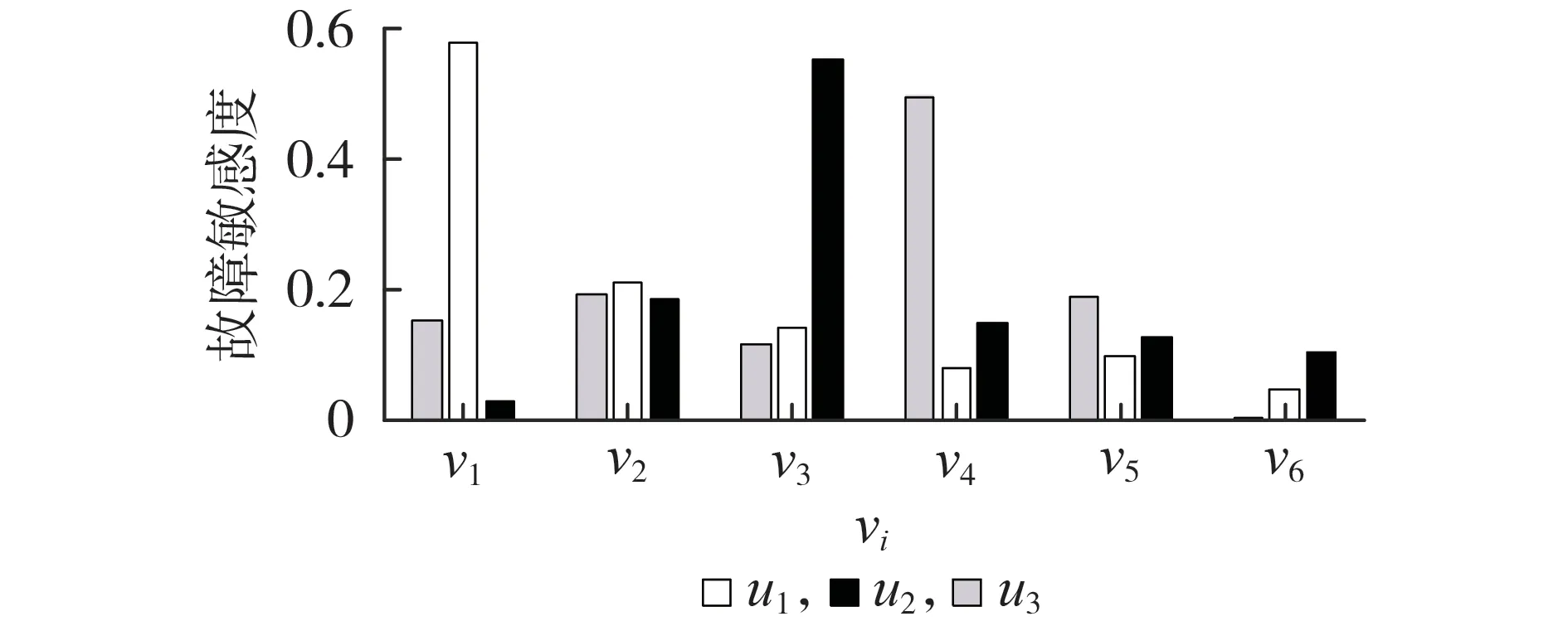
图4 不同部件状态信息的故障敏感度Fig.4 Fault sensitivity of different component status information

此外，选取3 个典型监测时刻τ1、τ2、τ3，由矩阵Hc分析得到这些典型监测时刻下不同状态信息的故障敏感度结果，见附录A图A8。

结合图4 和图A8 可以看出，在给定的几种故障类型中，齿轮箱齿弯曲故障u1中的状态信息冲击载荷位移v1最为灵敏，齿轮箱齿面胶合故障u2中的状态信息齿间润滑效果v3最为灵敏，而轴承过热故障u3中的状态信息润滑油温度v4最为灵敏。这表明不同状态信息指标对不同故障类型呈现出不同的敏感性，而本文方法有助于对不同故障的典型状态信息进行筛选与提取。

以状态信息v4丢失为例，分析轴承过热故障下的网络稳定性情况。结构洞数量随迭代次数的变化趋势见附录A 图A9。采用加权无标度网络方法得到经过迭代后的结构洞数量为37，多于未加权传统蒙特卡罗方法的结构洞数量22，这表明本文方法得到更多的结构洞，使得网络结构更加稳定，具有更强的鲁棒性。

5 结论

针对“智慧型”风电机组技术的快速发展，本文提出一种基于风电机组实时状态监测信息的动态可靠性评估模型，通过分析与验证得到的主要结论如下。

1）本文提出一种融合方法的改进贝叶斯网络模型的动态可靠性模型。算例分析表明，所提模型能够结合状态信息的实时变化，准确地计算机组的可靠性水平。

2）本文所提方法实现了对状态信息与“部件-状态”结构关联特性的表达，并能够推导出系统中各种状态信息对不同类型故障的敏感程度，同时减少了节点信息缺失可能给动态可靠性评估带来的不利影响，提升了鲁棒性。

3）基于无标度网络贡献度矩阵Lc构建的敏感度矩阵Hc，能够对不同故障的典型状态信息进行筛选与提取，可为构建风电机组快速准确的健康诊断系统提供参考。

可将单部件的贝叶斯网络建模思路和方法推广到多部件，从而构成更加复杂的多部件系统的贝叶斯网络模型。关于多部件的可靠性分析是下一阶段的研究工作。

附录见本刊网络版（http：//www.epae.cn）。