考虑频率与区间联络线功率安全约束的两区互联电力系统机组组合

申家锴，刘 洋，李卫东，顾泰宇，巴 宇，王海霞

（1. 大连理工大学 电气工程学院，辽宁 大连 116024；2. 国家电网公司东北分部，辽宁 沈阳 110180；3. 国网辽宁省电力有限公司电力科学研究院，辽宁 沈阳 110006）

0 引言

互联电力系统的日前调度包括联络线交易计划制定、机组组合等。我国电网主要采用分级调度模式，其中上级调度机构负责制定区间联络线交易计划，下级调度机构负责完成区域内的机组组合。随着“双碳”目标下新型电力系统的发展，由“双低”（低惯量、低一次调频能力）特征引发的频率稳定问题受到了广泛关注［1-3］，在机组组合中考虑频率稳定问题成为研究的热点之一［4］。与单一系统不同，互联电力系统的频率稳定控制需要区域之间的协同配合，由于各区资源的特性差异及分布差异，实际系统中，频率具有时空分布特征，区间联络线功率存在振荡［5-6］。由于区域调度机构无法事先获知相邻区域的开机方案，因而无法从整体考虑频率差异及功率振荡对系统安全的影响。考虑到上级调度机构的信息优势与协调作用，互联电力系统的频率及联络线功率安全校验可由其负责完成。

由于先前系统的频率差异与功率振荡并不显著，在制定机组组合方案时，可依据各区电网固定的频率调节系数来估计区间联络线功率增量，并基于统一频率模型估算频率最大偏移等［7-8］。这种忽略区域间运行状态变化的静态视角分析方法尽管存在一定偏差，但仍可接受。随着电源结构与电网形态的转变，频率时空分布特征更加显著［9-10］，再沿用静态视角分析方法制定机组组合方案将产生较大误差，可能导致误判而危及系统运行安全。以动态视角在机组组合中考虑频率稳定问题，关键是在安全约束中计入频率时空分布特征。已有的频率安全约束机组组合研究［11-17］大多基于统一频率假设，显然无法考虑这一特征因素。与已有研究相比，动态视角下互联电力系统安全约束机组组合的理论增量为：①在安全约束构建中，需基于互联电力系统频率响应模型考虑区域频率差异与区间联络线功率振荡；②在机组组合求解中，需根据调度模式考虑多个区域的多个非线性安全约束的协调。

就构建安全约束的解析安全量化指标而言，文献［18］基于扰动区与非扰动区的两区划分，建立了两机等值频率响应模型并推导了区域频率闭式解，但未给出区域频率最大变化率等安全指标的解析方法；文献［7］解析考虑了区间联络线功率准稳态值，但未考虑其峰值；文献［6］建立了两区联络线功率振荡模型并解析推导了区间联络线功率峰值表达式，文献［19-20］进一步研究了直流闭锁等故障下的功率峰值计算，但均未计及发电机的一次调频作用；文献［21］基于频域泰勒展开的方法推导了区域频率与区间联络线功率的多个安全量化指标表达式，但具备精度的表达式需要保留上百项，极其复杂。综上，目前仍然缺少能够准确描述区域频率与区间联络线功率安全的解析量化指标。

就互联电力系统安全约束机组组合的优化算法而言，由于目前关于互联电力系统的研究主要以提升经济性和灵活性为主，关注多区域间频率安全及资源互济的研究还较少［3］。文献［21］在考虑区域频率与区间联络线功率安全约束的机组组合中，采用了布尔函数法解决安全约束带来的非线性问题，但该方法空间复杂度爆炸，难以应用于大规模系统；针对频率安全约束非线性的两阶段迭代方法［15-17］，其有效性仅在基于统一频率假设的频率安全约束机组组合中被证明，但如何解决区域频率与区间联络线功率多个安全约束带来的非线性问题，以及如何根据调度模式在两阶段迭代中协调多个安全约束，还需进一步研究。综上，目前仍缺少针对互联电力系统的安全约束机组组合优化算法。

对此，本文针对两区互联电力系统安全约束机组组合展开研究，主要贡献如下。

1）基于两机等值频率响应模型进一步推导了区间联络线功率振荡首摆与准稳态闭式解；基于闭式解的快、慢变化项划分，推得区域频率最低点、最大变化率、准稳态值，以及区间联络线功率振荡峰值、准稳态值等解析安全量化指标。

2）基于所得指标建立了考虑区域频率与区间联络线功率安全的机组组合模型；基于指标的参数灵敏度分析，采用分段线性化方法构造了线性优化割；并基于各区参数对指标的影响，设计了安全约束的校验策略，提出了兼顾区域能力保障与区间能力协调的两级两阶段迭代求解算法。

1 两区互联电力系统的解析安全量化指标

互联电力系统中，区域频率最低点、最大变化率、准稳态值以及区间联络线功率振荡峰值、准稳态值等指标影响系统的安全稳定运行，并受各区开机方案的影响。本节将针对两区互联电力系统，基于两机等值频率响应模型，推导区域频率与区间联络线功率的解析安全量化指标。

1.1 两区互联电力系统频率响应模型

考虑到互联电力系统频率时空分布特征主要由区域间联系较弱导致的区域振荡模式产生，且频率动态由有功变化主导，假设各区内频率一致，分别将各区聚合为一台等值发电机。等值机组及互联电力系统部分参数定义如下：H、R、FH、TR和D分别为机组调速器的惯性时间常数、调差系数、高压缸做功比例、再热时间常数和等效阻尼；f、δ和Pm分别为频率、机组的功角和机械功率；Pd为扰动功率（功率盈余时为正，功率缺失时为负）；PP和PF分别为一次调频比例反馈与一阶惯性反馈环节功率；Km为发电机增益。后文中，变量左侧Δ表示对应变量的增量；上标“′”表示变量在两机等值模型中的对应参数；下标k（k=1，2）表示区域k。

含区外直流的两区互联电力系统示意图如图1（a）所示，基于直流潮流简化网络结构，并采用低阶调速器降低阶数，可得两机等值电力系统频率响应模型［17，21］，如图1（b）所示。图中：s为拉氏算子；B′S，1，1和B′S，2，1为机组间功率交换系数矩阵B′S中的元素；ω0为额定角速度；P′T为区间联络线功率（流出为正，流入为负）；ΔP′S，1，2和ΔP′S，2，1为机组间振荡功率矩阵ΔPS中的元素。

图1 含区外直流的两区互联电力系统及频率响应模型Fig.1 Two-area interconnected power system with DC outside area and its frequency response model

为方便计算，本文以SB为基准容量。区域k中发电机的增益系数Km，k，i为：

式中：κ为区域集合；Uk，i为区域k中机组i的启停状态变量，其值为0 表示停机，其值为1 表示开机；Pmax，k，i为区域k中机组i的额定功率；Vk为区域k中机组集合。

随着风电、光伏等可再生能源电站的一次调频功能改造［22］，可再生能源的调频控制应当被计及。当前，一次调频功能改造主要为在可再生能源电站有功功率控制系统中，增加模拟常规机组调频特性的频率控制环节（虚拟惯性控制与下垂控制）。由于添加的频率控制环节与常规机组具有相似结构，可与常规机组同时等值聚合［15-17］。图1（b）中调速器参数的等值聚合公式见附录A式（A1）、（A2）。

定义扰动所在区域为扰动区，相邻区域为非扰动区，本文设区域1为扰动区，则区域2为非扰动区。区间联络线功率增量ΔP′T为非扰动区对扰动区的支援功率，等于扰动区电磁功率增量。根据图1（b），区域1 中电磁功率增量ΔP′T为ΔP′S，1，2与ΔP′d，1之差，如式（2）所示。

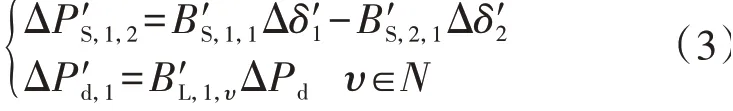
式中：B′L，1，υ为区域1 中初始扰动功率分配矩阵B′L的元素；N为系统节点集合；υ为扰动发生节点。由文献［18］可知机组间功率交换系数矩阵B′S与初始扰动功率分配矩阵B′L中的元素分别存在如下关系：

式 中：BS，i，τ为 机 组i、τ间 的 功 率 交 换 系 数。由 于B′S，1，1=B′S，2，2=-B′S，1，2=-B′S，2，1，为方便后文计算，记w′=ω0B′S，1，1。

1.2 模型闭式解

1.2.1 模型的振动方程与区域频率闭式解

图1（b）所示模型为2 个3 阶系统互联组成的6阶系统，无法直接求取闭式解。为解决考虑区间关系与调速器动态带来的高阶问题，根据调速器一阶惯性反馈环节增量ΔP′F，k的低通滤波特性，采用文献［18］提出的频率反馈解环、频率近似替代、模态分解等方法，可将该模型系统动态方程转换为以y1(t)、y2(t)为主模态坐标的二阶二自由度强迫振动方程，如式（5）所示。

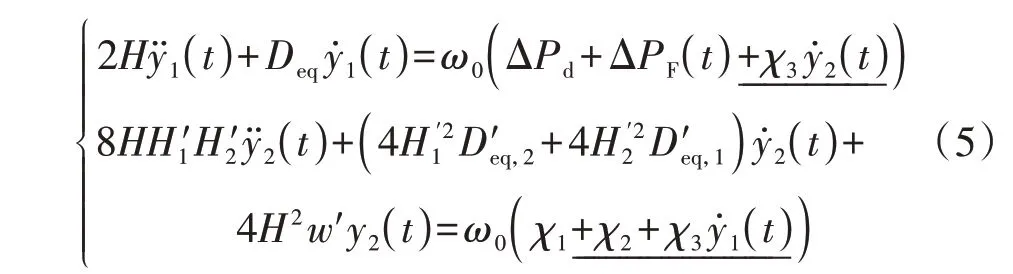
式中：Deq=D+KmFH/R，D′eq，k=D′k+K′m，kF′H，k/R′k；等号左侧的系数2H与8HH′1H′2为模态质量，Deq与4H′21D′eq，2+4H′22D′eq，1为模态阻尼，4H2w′为模态刚度系数；等号右侧为模态坐标下的强迫输入，ΔPd与χ1为初始扰动产生的强迫输入，ΔPF(t)与χ2为调速器一阶惯性反馈环节产生的强迫输入，χ3y˙1(t)与χ3y˙2(t)为模态阻尼矩阵非对角元素产生的强迫输入，带下划线的表达式为标记项。χ1、χ2、χ3的表达式分别为：

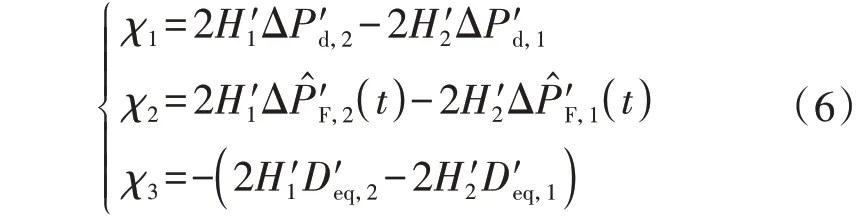
式中：变量上方“＾”表示变量的近似值。频率、模态坐标与模态矩阵Φ的关系如下：

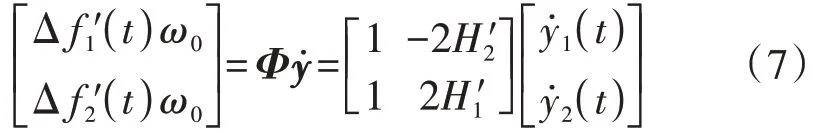
经验证，在式（5）中χ3y˙2(t)对y˙1(t)影响很小，χ2与χ3y˙1(t)对y˙2(t)影响很小。忽略标记项，可解耦y1(t)与y2(t)；分 别 求 解y˙1(t)与y˙2(t)，然 后 代 入 式（7），则可得区域频率闭式解；对闭式解求导可得区域频率变化率闭式解。闭式解的详细求解过程见附录B式（B1）—（B8）。

1.2.2 区间联络线功率闭式解

联立式（2）、（3）、（7），可得机组间振荡功率ΔP′S，1，2(t)与模态坐标的关系为：

图2 区间联络线功率振荡的仿真值与解析值对比Fig.2 Comparison of simulative value and analytical value of inter-area tie-line power oscillation

经验证，该偏差由求解式（B2）、（B4）时忽略标记项引起。这些标记项对区域频率影响很小，但其积分对区间联络线功率影响显著，因此在求解区间联络线功率闭式解时应被考虑。然而计及上述标记项会导致方程变量的耦合，无法解析。考虑到求解闭式解的目的为求取安全量化指标，可根据待求指标特点采取针对性简化。需要说明的是，由于后续推导结果仅与y˙1(t)有关而与y1(t)无关，且χ3y˙2(t)对y˙1(t)影响很小，因此χ3y˙2(t)将被继续忽略。

1）区间联络线功率振荡首摆。

区间联络线功率最大值出现在区间联络线功率振荡的首摆峰值［6］。在该时间尺度内，可作如下假设：

（1）假设1，调速器时间常数较大，可认为调速器一阶惯性环节未响应，仅考虑比例反馈环节，即ΔPF(t)与ΔP′F，k(t)恒为0；

（2）假设2，频率下降斜率变化缓慢，可采用初始下降斜率近似。

基于假设1，忽略式（5）中的ΔPF(t)及含ΔP′F，k(t)的χ2；基于假设2，忽略式（5）中Deqy˙1(t)。则式（5）可以改写为：

式中：Atan（·）为自定义的方位角函数，其表达式见附录B式（B9）。

2）区间联络线功率准稳态值。

对于准稳态而言，动态过渡过程已结束，区间联络线功率和区域频率均达到准稳态值。此时所有动态元件的时间常数均不再起延迟作用，即等效为0。设该时刻为t∞，则y˙1(t∞)与y2(t∞)均为常数，y¨1(t∞)与y˙2(t∞)均为0，将上述参数代入式（5），可得准稳态频率闭式解Δf′ss(t)为：

1.3 解析安全量化指标

本节将基于所得闭式解推导区域频率最低点、最大变化率、准稳态值以及区间联络线功率振荡峰值、准稳态值等关键特征的解析安全量化指标。

对于区域频率与区间联络线功率准稳态值，由于式（12）、（14）所示闭式解恒为常数，因此式（12）、（14）分别为区域频率与区间联络线功率准稳态值的解析安全量化指标。对于区域频率最低点、最大变化率以及区间联络线功率振荡峰值，由于式（B2）、（B4）及式（B6）、（B7）与式（10）所示闭式解仍为超越函数构成的超越方程，无法直接解析，因此本节将基于闭式解的快变项、慢变项划分，推导安全量化指标的近似解析值。

1.3.1 基于快变项、慢变项划分的解析求解方法

由式（B2）、（B4）及式（B6）、（B7）与式（10）可以看出，表达式均由不同角频率的函数组成（常数项、一次项和指数项角频率为0）。根据角频率大小，表达式可被分为快变项（角频率大）与慢变项（角频率小）。依据该方法，划分结果如下：式（B2）、（B4）及式（B6）、（B7）中第1 项为慢变项，第2 项为快变项；式（10）前2项为慢变项，第3项为快变项。设原闭式解描述的为原曲线，则原曲线以及划分后的快、慢变项曲线如图3 所示。由图可知，原曲线的极点时刻很大程度上由快变项直接决定，受慢变项影响不大。基于该特征，在求解原曲线极点时采用快变项曲线的极点时刻近似替代原曲线的极点时刻，可得具有较高精度的近似极点。下面基于该近似方法推导解析安全量化指标。

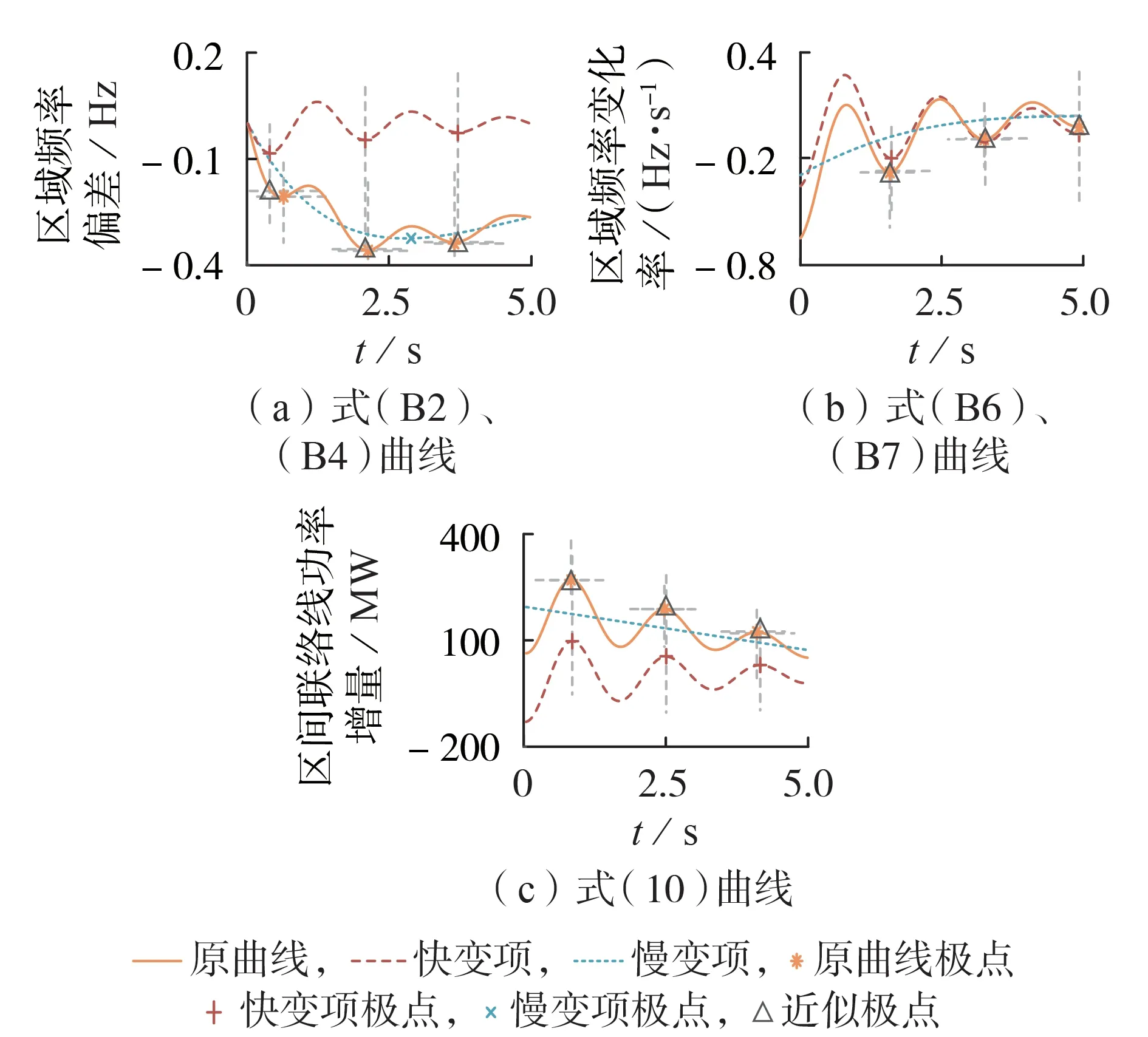
图3 原曲线分解与极值点近似示意图Fig.3 Schematic diagram of original curve decomposition and extreme point approximation

1.3.2 区域频率安全量化指标1）频率最低点。

当大功率缺失故障发生后，受频率时空分布特征影响，频率最低点相较系统频率最低点向下偏移，如图3（a）所示（图中原曲线的最小极点、慢变项曲线的最小极点分别表示频率最低点和系统频率最低点）。在参数取值范围内仿真发现，由于快变项曲线振荡是衰减的，且振荡幅值小于慢变项曲线的偏移幅值，因此频率最低点会出现在慢变项曲线极小值点对应时刻前后的快变项曲线极小值点时刻。

分别令式（B6）、（B7）中慢变项与快变项为0，可得慢变项与快变项极小值点时刻的表达式分别为：

1.3.3 区间联络线功率安全量化指标

区间联络线功率振荡最大值为首摆振荡峰值，即为式（10）的首个极值点，同样可依据该式快变项曲线的极值点时刻近似求取。式（10）快变项导数为：

2 机组组合

本节将基于解析安全量化指标，针对两区互联电力系统，构建考虑区域频率与区间联络线功率安全的机组组合模型，并根据指标特点，设计多个安全约束的校验策略，分别构建线性优化割，进而提出兼顾区域能力保障与区间能力协调的两级两阶段迭代求解算法。

2.1 目标函数

为了在机组组合中最大化消纳可再生能源，本文将可再生能源作为无发电成本资源［15-16］，综合考虑区域内常规机组的发电成本、启停成本，构建目标函数如下：

式中：ak，i、bk，i、ck，i为区域k机组i的发电成本系数；dk，i为区域k机组i开机成本；Pk，i，j为区域k机组i调度时段j（j=1，2，…，T）的出力，T为调度周期总时段数；Uk，i，j为区域k机组i调度时段j的启停状态。

2.2 约束条件

本文根据由大功率扰动故障组成的预想故障集构建安全约束条件。根据安全稳定导则［23］，本文考虑的预想故障包括直流闭锁、大容量发电机跳闸、大负荷突然变化等单一元件造成的大幅功率波动。

为保证机组组合方案的频率安全，需保证区域频率及区间联络线功率等安全指标在所有预想故障下均不越限。安全约束包括区域频率的最低点约束、最大变化率约束、准稳态约束以及联络线功率的峰值约束、准稳态约束等。基于解析安全量化指标，构建安全约束如式（28）—（32）所示。

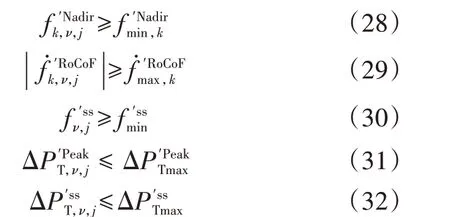
除安全约束外，还应考虑功率平衡约束、常规机组出力约束、风电出力约束、爬坡约束、最小开机时间约束、最小停机时间约束、备用容量约束、最大弃风量约束等常规约束，分别如附录C 式（C1）—（C8）所示。

2.3 优化求解算法

由于式（28）—（32）为非线性约束，本文机组组合为包含多个非线性安全约束的混合整数非线性规划问题。考虑到上级调度机构的协调作用，以及多个非线性约束的变化特点，依据基于主子问题划分的两阶段迭代方法［15-17］，提出如下求解算法。

1）基于两级调度的主子问题划分。

基于两阶段迭代求解思路，分级调度模式下机组组合的主子问题划分如下：主问题为已知联络线交换功率的区域内机组组合，包括目标函数式（26）与常规约束式（C1）—（C8），为混合整数线性规划问题，该问题由下级调度机构完成并将结果上传至上级调度机构；子问题为已知机组组合方案的区域频率与区间联络线功率安全约束校验，包括式（28）—（32），为非线性约束校验问题，由上级调度机构完成；优化割为连接主子问题的补充约束，作用为缩小优化求解的可行域，当校验不合格时由上级调度机构更新后下发给下级调度机构。

2）多个安全约束的线性化优化割构造。

根据3.1 节安全量化指标的参数灵敏度分析结果，本文进一步将子问题校验分为3 个子校验阶段。子校验1 由式（31）、（32）组成，目的为保证联络线功率安全，方式为更新扰动区不合格约束对应的优化割；子校验2 为式（29），目的为提升本区域的惯性响应能力，方式为更新约束不合格区域对应的优化割；子校验3 由式（28）、（30）组成，目的为提升系统整体调频能力，方式为更新调频成本增加较少区域的不合格约束对应的优化割。Flag初始值为1，表示扰动区1，求解流程如附录C 图C1 所示。当预想故障中存在造成后果最为严重的功率扰动时，在子问题安全校验中仅校验该扰动即可。

3 算例分析

为便于对解析安全量化指标做范围更广的参数灵敏度分析及鲁棒性验证，本文在算例1 采用结构较简单的IEEE 两区4 机系统；为便于验证本文所建机组组合模型及所提求解算法的有效性，在算例2中采用了机组较多、规模较大的IEEE 两区96 节点系统。

3.1 安全量化指标验证与分析

IEEE 两区4 机系统见附录D 图D1，基本参数取自文献［18］，其中动态参数及取值范围见附录D 表D1。设系统扰动为初始时刻7 号节点（区域1）的300 MW 负荷突增为系统容量的7.5%。安全指标的参数灵敏度分析及对比采用控制变量法进行（改变区域1 或区域2 模型的动态参数）。需要说明的是，由于无论系统规模大小，基于系统容量的参数标幺值均落在相同范围，因此基于该取值范围进行参数灵敏度分析可保证结论的普适性。

分别采用仿真方法（SIM-ASI，标杆值）、本文方法（TEFR-ASI）、统一频率解析方法［8］（SFR-ASI）、区间联络线功率解析方法（REF-ASI，峰值与稳态值计算方法分别来自文献［20］和文献［7］）等不同方法计算频率与区间联络线功率安全量化指标的参数灵敏度，结果分析见附录E图E1—E3。由图可得主要结论如下。

1）稳态指标不受频率时空分布特征的影响，各方法所得稳态指标结果相同。除此以外，与SFRASI方法以及REF-ASI方法相比，本文方法的准确性大幅提升，指标精度最少提升67%，最多提升99.47%。

2）增加系统调频能力的优先原则为：对于频率最大变化率安全指标，优先考虑本区域成本较低的调频资源；对于频率最低点与准稳态安全指标，优先增加任意区域中成本较低的调频资源；对于区间联络线功率安全指标，优先增加扰动区成本较低的调频资源。此外，安全指标的变化具有分段线性特征，可依据分段线性化方法进行进一步的线性化处理。

3.2 机组组合方案分析

3.2.1 方案设计与基础数据

IEEE 两区96 节点系统见文献［24］。该模型含有2 个区域、66 台发电机组，其中区域1 含有域外直流输入，并通过交流联络线与区域2 相连。为计及可再生能源参与调频，分别在节点11、19、35、43 接入300 MW 风电机组，改进后系统如附录F 图F1所示。算例基本参数取自文献［24-25］。此外，机组动态参数见附录F 表F1，日内小时负荷系数见附录F 表F2，节点负荷系数见附录F 表F3，日联络线功率交换计划见附录F 图F2，日风电功率预测见附录F 图F3，区域1 与区域2 的日总负荷分别设为75 400、44 400 MW。系统线性优化割系数如附录F表F4所示。

设直流闭锁为系统遭遇的最严重扰动，系统允许的频率最低点、准稳态值、最大频率下降斜率分别为49.25 Hz、49.68 Hz、1 Hz／s，区间联络线功率波动允许的最大峰值与准稳态值分别为520、390 MW，备用容量系数与弃风系数为5%。

为分析机组组合求解过程，验证机组组合模型的有效性，本文设置4种对比方案：①方案1，不考虑区域频率与区间联络线功率安全约束的机组组合；②方案2，在方案1的基础上考虑区域频率最大变化率安全约束的机组组合；③方案3，在方案1 的基础上考虑区域频率最低点与准稳态安全约束的机组组合；④方案4，在方案2、3的基础上，考虑区间联络线功率峰值与准稳态值安全约束的机组组合。设机组组合调度时段为［1，24］，每个调度时段为1 h。基于MATLAB 平台，采用YALMIP 工具箱调用CPLEX 12.10求解。

3.2.2 4种方案下的机组组合结果分析

4种方案在时段［10，16］的机组启停如附录G图G1、G2 所示。分别计算各方案下24 个时段区域1（2）频率最低点Δf˙′Nadir1(Δf˙′Nadir2)、区域1 频率最大变化率Δf˙′RoCoF1、准稳态值Δfss以及联络线功率增量峰值ΔP′PeakT、准稳态值ΔP′ssT，结果如图4 所示。需要说明的是，由于区域2 中频率最大变化率始终小于允许值，因此后续不再分析。

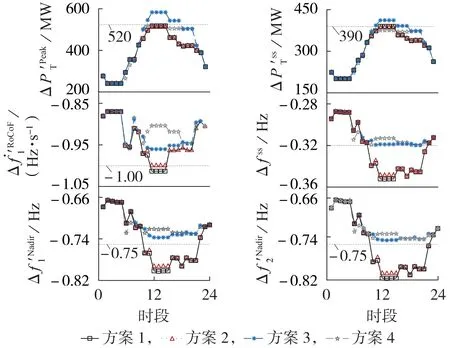
图4 4种方案的频率与联络线功率安全指标Fig.4 Frequency and tie-line power safety indicators under four schemes

可以看出，方案1 中2 个区域开机数量均较少，系统频率响应能力明显不足，扰动后多个时段的区域频率最低点、准稳态值以及时段［12，15］中区域1的频率最大变化率均不满足安全约束。区间联络线功率稳态值与峰值虽未超过允许值，但多个时段已非常贴近，优化不当可能导致越限。

相较方案1，方案2 结果增加了区域1 的开机数量，有效提升了惯性响应能力，使得扰动后区域1 的频率最大变化率下降至允许范围，频率最低点与准稳态值等指标虽有一定改善，但仍然越限。相较方案1、2，方案3 同时在2 个区域增加了更多机组，系统频率遏制能力得到大幅提升，各区域频率最低点、稳态值均被抬升至安全范围，但由于未考虑两区的协调能力，区间联络线功率波动峰值与准稳态值大幅增加，出现越限现象。

方案2、3 中，区域频率变化率约束与区域频率最低点约束在保障区域频率安全上分别发挥了良好作用，但一味增加两区开机数量而不做协调可能会导致区间联络线功率安全指标越限。相较方案2、3，方案4结果适当增加了区域1机组的开机数量，减小了区域2 机组的开机数量，在提升区域频率指标安全水平的同时，有效降低了区间联络线功率峰值与准稳态值，全面保障了区域频率与区间联络线功率安全。

4 种方案的发电成本对比如表1 所示，方案4 的发电成本增加最多，方案3、2 次之。这是由于为保证扰动后的区域频率或区间联络线功率稳定，方案2—4均依次增开了更多发电机组，导致发电成本有所提升。

表1 4种方案发电成本对比Table 1 Comparison of power generation cost under four schemes

3.2.3 机组组合求解过程分析

为更加清晰地说明本文求解算法的有效性，下面给出方案4 的优化求解过程，如图5 所示。由图可知：整个优化求解过程进行了37 次迭代，可分为①—⑦这7 个部分，其中，⑦为结束判断，其余分别对应于3 个子校验阶段，更新不同优化割指标。具体而言：①、④针对区间联络线功率指标；②针对区域频率最大变化率指标；③、⑤、⑥针对区域频率最低点及准稳态值指标。可以看出：在优化求解的过程中，每当区间联络线功率指标越限，均能被及时限制在安全范围；每当区域频率最大变化率需要减小，均可优先选取本地资源；每当区域频率最低点与准稳态需要提升，均可灵活选取各区资源。因此，本文所提两级协调的两阶段迭代算法能够实现区域能力保障与区间能力协调，从而保障系统区域频率与区间联络线功率的安全稳定运行。

图5 方案4机组组合模型优化求解过程Fig.5 Optimization solution process of unit commitment model under Scheme 4

4 结论

本文针对两区互联系统频率安全，在解析安全量化指标推导中考虑了频率时空分布特征的影响，基于所得指标建立了两区互联电力系统安全约束机组组合模型并提出了求解算法。所得结论如下：

1）基于两机等值频率响应模型进一步推导所得解析安全量化指标，与统一频率指标相比，不仅可准确描述两区互联电力系统区域频率最低点、最大变化率、准稳态值，还可准确描述区间联络线功率变化峰值、准稳态值等安全特征，且具有较强鲁棒性；

2）基于指标参数灵敏度分析所得增加调频能力的优先原则，相比经济优先原则，能够考虑资源位置的影响，调频资源选择的目的性更强、效率更高，可为调度决策提供支撑；

3）依据优先原则提出的两级协调的两阶段迭代求解算法，可利用两级调度机构的协作关系，完成频率与区间联络线功率等多个安全约束的有序校验，实现系统能力的保障与协调，更好地维护两区互联电力系统的频率安全。

本文针对两区系统展开，其研究框架与范式同样可适用于多区互联电力系统。随着多机频率响应解析分析方法的突破，在本文研究的基础上，后续可进一步开展多区互联电力系统的机组组合研究。

附录见本刊网络版（http：//www.epae.cn）。