基于阻抗偏差最小判据和改进自适应蝙蝠算法的系统侧谐波阻抗估计方法

程卫健，林顺富，许亮峰，刘持涛，李东东，符 杨

（1. 上海电力大学 电气工程学院，上海 200090；2. 国网上海市电力公司青浦供电公司，上海 201700）

0 引言

随着电力系统中新能源渗透率的不断提高与非线性负荷的大量增加，谐波污染问题愈发严重，电力谐波已成为公共电网亟待解决的问题之一［1-2］。为了实现对电力谐波的有效治理，有必要合理量化供用电双方的谐波责任。而系统侧谐波阻抗估计是谐波责任划分的关键步骤之一，对于谐波治理具有重要意义［3］。

典型的谐波阻抗估计方法包括波动量法［4-5］、协方差法［6］、盲源分离法［7-9］、回归分析法［10-12］等。以上方法多基于一定的前提，例如：①系统侧谐波阻抗在分析时段内恒定；②用户侧谐波阻抗远大于系统侧谐波阻抗；③背景谐波波动较小。随着现代电网新能源渗透率的不断增加，以上前提逐渐难以被满足。系统运行方式的改变、设备的投切和无功补偿方式的变化都可能导致系统侧谐波阻抗发生大幅度突变。当用户侧存在新能源并网时，由于并网侧多配置滤波器和无功补偿设备，可能导致用户侧谐波阻抗不再远大于系统侧谐波阻抗。此外，新能源的谐波发射具有更强的随机性和波动性，当系统侧存在新能源并网时，背景谐波电压将具有更大的波动性。基于以上因素，系统侧谐波阻抗估计问题面临巨大的挑战。

文献［13］和文献［14］分别采用斜率比较法和小波变换模极大值法辨识阻抗突变的时间点，从而分段求解系统侧谐波阻抗，但这2 种方法均未考虑背景谐波波动的影响。文献［15］筛选出谐波电压和电流间的弱相关时刻，从而削弱背景谐波波动的影响；文献［16］构造最小背景谐波波动能量目标函数，筛选出背景谐波波动最平稳的样本点，在此基础上估计系统侧谐波阻抗。但当背景谐波电压在分析时段内始终保持较大的波动时，这2 种方法难以筛选出满足要求的样本点。文献［17］根据背景谐波电压的大小对谐波数据进行分组，使得每组数据对应的背景谐波波动平缓，比数据筛选类方法具有更大的适用范围。然而文献［17］的方法对公共连接点PCC（Point of Common Coupling）处的复数谐波相量进行实虚部分解，从而在实数域上求解系统侧谐波阻抗，不可避免地引入了一定误差；且该方法在寻优过程中采用固定步长寻优策略，易陷入局部最优解。文献［11］直接在复数域上求解系统侧谐波阻抗，避免了实虚部分解所带来的误差影响，但该方法所得估计值的准确性基于背景谐波恒定的前提。

考虑到系统侧谐波阻抗估计结果对背景谐波波动敏感和实虚部分开求解影响估计精度的问题，本文结合文献［11］和文献［17］的相关思想，直接在复数域对谐波数据进行分组并求取系统侧谐波阻抗；同时，考虑到寻优过程对系统侧谐波阻抗估计值的结果影响较大，采用改进自适应蝙蝠算法进行寻优操作。蝙蝠算法可实现全局搜索到局部搜索的自动转换，具备模型简单、进化效率高、鲁棒性强等优点，被广泛应用于工程实践。改进自适应蝙蝠算法克服了标准蝙蝠算法后期收敛速度慢、易陷入局部最优等缺点，进一步提高了系统侧谐波阻抗估计的准确性。多个算例分析结果验证了本文所提方法的有效性和适用性。

1 方法原理

当仅关注单一谐波源的谐波发射问题时，可将关注用户等效为用户侧，其他部分都等效为系统侧，单用户谐波分析模型可以等效为图1 所示的等效电路。图中：Upcc和Ipcc分别为PCC 处的谐波电压和谐波电流；Zs和Zc分别为系统侧和用户侧的等效谐波阻抗；Us为背景谐波电压；Ic为用户侧等效谐波电流。

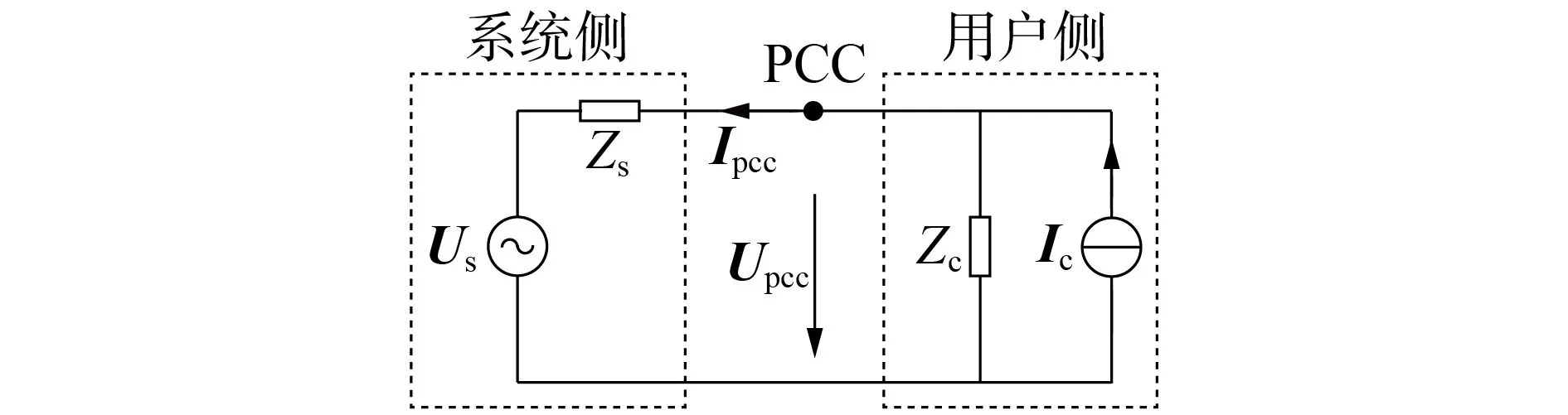
图1 谐波分析等效电路Fig.1 Equivalent circuit for harmonic analysis

基于图1分析可得等效电路方程如式（1）所示。

基于式（1）构建回归方程，可通过回归分析法求解Zs［10］。由于式（1）中各变量均为复数，传统的回归分析法将式（1）按实虚部展开为2 个方程，分别求解Zs的实部和虚部。文献［18］指出，实虚部分开进行回归求解得到的使得各自方程误差平方和最小的最小二乘解并非原问题的整体最小二乘解。而在复数域直接进行回归计算，其回归结果误差模的平方和具有更小值。基于此，文献［11］采用复最小二乘法求解Zs，其估计结果更接近真实值。复最小二乘法的计算步骤如下。

首先，将式（1）改写为式（2）所示的矩阵形式。

回归系数矩阵X在复数域上的最小二乘解可由式（4）得到。

式中：inv（·）表示矩阵求逆运算；上标H 表示共轭转置。

在得到回归系数的前提下，可由式（5）得到系统侧谐波阻抗估计值Ẑs。

复最小二乘法进一步提高了线性回归的估计精度，但其准确求解的前提是分析时段内系统侧谐波阻抗和背景谐波电压值基本不变，而实际情况下背景谐波电压具有一定的波动性。当背景谐波电压波动较大时，该方法的计算结果与实际值偏差较大，难以满足实际应用需要。

考虑到背景谐波波动性对系统侧谐波阻抗估计的影响，若能将PCC 谐波采样数据按照背景谐波电压的大小进行分组，使得每组数据的背景谐波电压值波动平缓，则各组数据采用复最小二乘法求得的系统侧谐波阻抗估计值将更接近真实值。由于在复数域内无法直接通过大小排序等方法对背景谐波电压值进行分组，本文通过K-means 聚类算法进行聚类处理使得每簇内的Us波动较小，K-means 聚类算法的具体流程如附录A图A1所示。

K-means聚类算法要求提前给定聚类数目m，可采用手肘法、DBI 法或轮廓系数法确定m值。文献［19］给出了一种简便的经验公式来确定m值，其表达式如式（6）所示。

式中：n为样本个数。

考虑到若聚类后簇内数据量过少，回归算法难以得到准确的估计值，设定m值的上限为n/50，则m值的最终取值为：

式中：floor（·）表示向下取整运算。

以上分析是基于背景谐波电压Us已知的前提，而实际情况下Us为未知量，需要通过间接的方式进行分析。首先，可随机给定系统侧谐波阻抗初值Zs0，根据式（1）求解其对应的背景谐波电压值Us。对Us进行K-means 聚类操作，并根据聚类结果将对应的PCC 谐波样本数据划分为m簇。对于每簇数据，分别采用复最小二乘法求得相应的系统侧谐波阻抗估计值（i=1，2，…，m），定义与Zs0之间的偏差Vdev如式（8）所示。

偏差Vdev与系统侧谐波阻抗初值Zs0之间并非光滑函数关系，如果寻优策略不合适，则极易陷入局部最优解，使得误差增大。因此，本文选用改进自适应蝙蝠算法进行寻优计算以得到更精确的系统侧谐波阻抗估计结果，图2 给出了本文所提方法的基本流程。

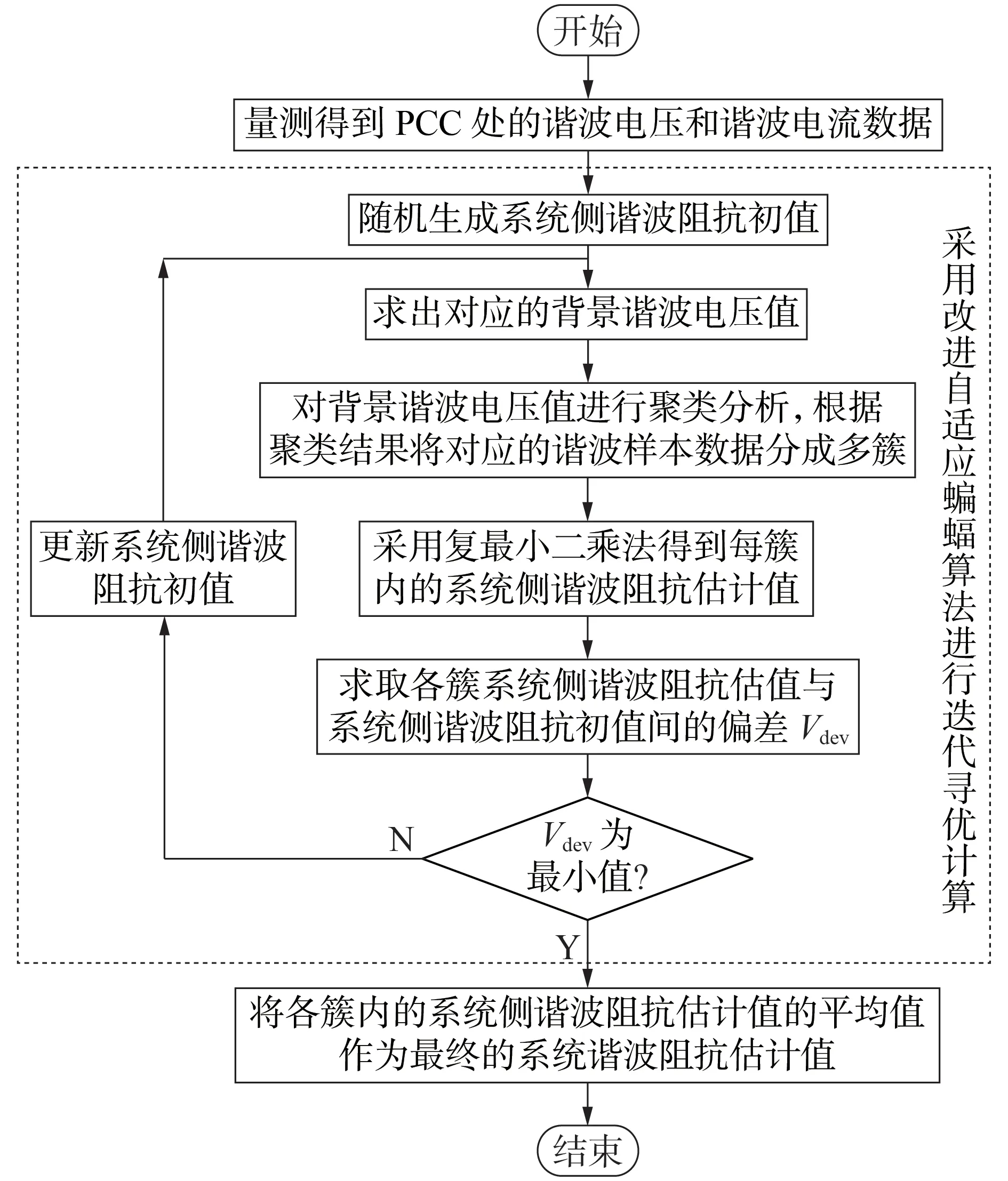
图2 本文所提方法的流程图Fig.2 Flowchart of proposed method

2 改进自适应蝙蝠算法

蝙蝠算法在寻优过程中可实现从全局搜索到局部搜索的自动转换，具备模型简单、进化效率高、鲁棒性强等优点，适用于复杂目标函数下的寻优运算。但标准蝙蝠算法存在后期收敛速度慢、易陷入局部最优等缺点，限制了其进一步应用［20］。

为克服标准蝙蝠算法的固有缺陷，提高寻优结果的精确度，本文对标准蝙蝠算法进行优化，提出了一种改进自适应蝙蝠算法：首先，通过混沌映射策略提高蝙蝠初始种群的多样性，并采用自适应步长控制机制提高算法的求解精度［21-22］；为了避免算法在寻优过程中过早陷入局部收敛，引入自适应变异机制以及时跳出局部最优解［23］。改进自适应蝙蝠算法的具体运算过程如附录B所示。

本文以系统侧谐波阻抗初值Zs0为变量，以偏差Vdev为适应度值，采用改进自适应蝙蝠算法进行迭代寻优，得到使Vdev最小的Zs0值，从而进一步得到系统侧谐波阻抗的精确估计值。在寻优过程中，设定蝙蝠个体维度为2，分别代表Zs0的实部和虚部。设置蝙蝠种群规模Nbat=40，最大迭代次数tmax=100。算法终止条件为最优解的凝滞步数达到10 或迭代次数t=tmax。

3 算例分析

3.1 诺顿等效模型算例分析

参考文献［17］建立诺顿等效仿真模型以验证本文所提方法的有效性，具体仿真参数设置如下。

1）用户侧等效谐波电流源：Ic的幅值Ic=100 A；Ic的相角∠Ic=-60°；在Ic上叠加±15%Ic的随机扰动和±20%Ic的正弦波动，在∠Ic上叠加±40%∠Ic的随机扰动。

2）系统侧等效谐波电流源：系统侧等效谐波电流Is的幅值Is=kIc，其中k的取值为0.1、0.3、0.5、0.8、1，且k值越大，背景谐波波动越大；Is的相角∠Is=60°；在Is上叠加±15%Is的随机扰动，在∠Is上叠加±40%∠Is的随机扰动。

3）谐波阻抗：Zs=5+j10 Ω；Zc=pZs，其中p的取值为1、1.5、3、5、7、9；Zs与Zc的实、虚部均添加±10%的随机扰动。

按照以上设置仿真得到3000个数据点，分别采用4种方法估算系统侧谐波阻抗：方法1为复最小二乘法［11］；方法2 为主导波动量法［5］；方法3 为文献［17］所提方法；方法4 为本文方法，且由式（7）计算得到m=38。利用式（10）计算各方法的系统侧谐波阻抗相对估计误差Erel（下文简称相对估计误差）以评价各方法的估计精度。

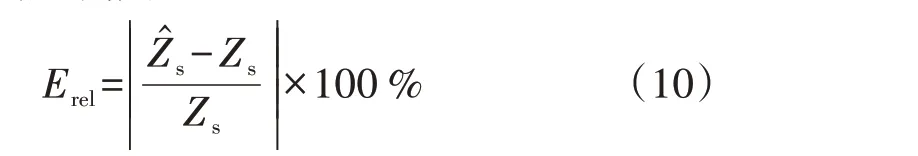
附录C图C1给出了不同阻抗初值Zs0条件下，偏差Vdev的计算结果。图中，k、p取值分别为0.5 和3。由图可见，当系统侧谐波阻抗初值Zs0与Zs的真实值相近时，偏差Vdev接近最低值。可以Vdev最小为寻优目标，得到接近Zs真实值的最优系统侧谐波阻抗初值，从而进一步计算更精确的系统侧谐波阻抗估计值。

为了评估背景谐波的波动大小对4 种方法的估计效果的影响，固定p值以给出不同k值下4 种方法的相对估计误差。固定p=7的情况下，Zc=35+j70 Ω，此时用户侧谐波阻抗远大于系统侧谐波阻抗，4 种方法的相对估计误差如图3 所示。固定p=1.5 的情况下，Zc=7.5+j15 Ω，两侧谐波阻抗相近，此时4 种方法的相对估计误差如附录C图C2所示。由图3和图C2 可以看出，在这2 种场景下，随着k的增大，4 种方法的相对估计误差都增大，但误差的大小和增长率有所不同：方法1、2 对k值非常敏感，其相对估计误差随着k值的增长而急剧增大；与方法1、2 相比，方法3、4 具有更小的相对估计误差且误差增长更平缓；方法4 的相对估计误差始终低于其他3 种方法，且对于背景谐波波动的变化具有更强的鲁棒性，具有更好的系统侧谐波阻抗估计效果。

图3 p=7时4种方法的相对估计误差对比Fig.3 Comparison of relative estimation errors among four methods when p is 7

为了进一步验证各方法对两侧谐波阻抗比p的敏感程度，分别固定k值为0.3和1，分析背景谐波波动较小和较大时，各方法在不同p值下的有效性。k=0.3和k=1时，4种方法的相对估计误差分别如图4和附录C 图C3所示。由图4和图C3可以看出：随着p值的减小，4 种方法的相对估计误差都增大；方法1、2对p值敏感，其估计结果随p值的变化波动较大。方法3、4 对p值的变化具有更强的鲁棒性，在p值较小的情况下仍能保持较低的相对估计误差，且方法4的估计结果始终更接近真实值。

图4 k=0.3时4种方法的相对估计误差对比Fig.4 Comparison of relative estimation errors among four methods when k is 0.3

为了更直观地展现所提方法的优越性，以p为X轴，以k为Y轴，以Erel为Z轴，绘制三维对比图如附录C图C4所示。由图可见：在不同场景下，方法4的相对估计误差小于其他3 种方法的相对估计误差；方法4对k、p的变化具有更强的鲁棒性，在背景谐波波动较大和用户侧谐波阻抗非远大于系统侧谐波阻抗的情况下可得到更精确的系统侧谐波阻抗估计结果。

3.2 三馈线模型算例分析

本节建立典型三馈线模型以分析4 种方法在多谐波源场景下进行系统侧谐波阻抗估计的有效性，仿真电路模型如附录D 图D1 所示。图中：Zci和Ii（i=1，2，3）分别为用户侧馈线i的等效谐波阻抗和等效谐波电流源；Ici为馈线i所在支路的量测电流相量。仿真电路模型的具体参数设置如附录D表D1所示。仿真中在系统侧、用户侧各谐波源的幅值和相角中均添加±40%的随机波动，仿真共采样3 000 个数据点。

分别采用4 种方法估计PCC 和各馈线的等效系统侧谐波阻抗值，结果如表1 所示。由表中的数据可以看出，在多谐波源场景下，方法4 的估计值更接近理论值，说明本文方法的估计结果比其他3 种方法更准确。

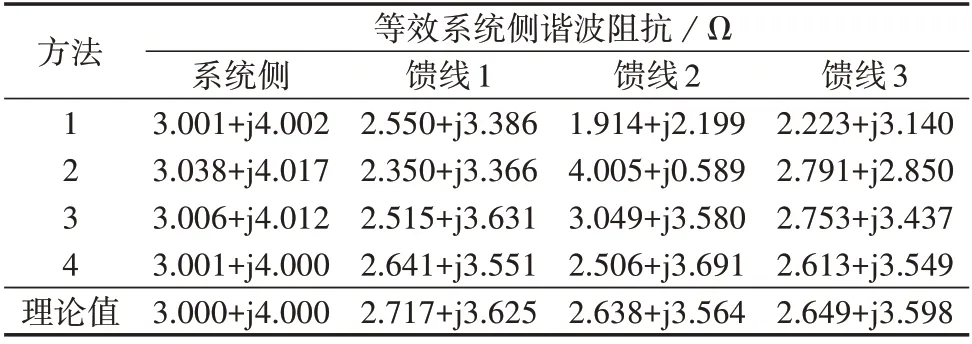
表1 4种方法的系统侧谐波阻抗估计结果Table 1 Estimation results of system-side harmonicimpedance with four methods

为了更清晰地体现各方法的系统侧谐波阻抗估计性能，采用图5所示的柱状图来展示4种方法在系统侧和各馈线处的相对估计误差。由图可见，方法4 在系统侧和各馈线的相对估计误差始终是4 种方法中最小的，说明本文方法在多谐波源场景下依然具有较高的准确性。

图5 各方法的相对估计误差柱状图Fig.5 Histogram of relative estimation error with each method

3.3 典型中／低压电网基准测试系统算例分析

谐波分析、谐波责任划分等方向的研究需要一个一致的测试系统以验证各类方法的有效性。鉴于这一需求，IEEE-PES 提供了一个为工业负荷供电的典型中／低压电网基准测试系统以进行谐波建模和算例分析，该基准测试系统的基本模型见附录E 图E1。图中，负荷1 和负荷2 建模为三相晶闸管整流器，分别为PCC 处用户侧和系统侧的主要谐波源。本节基于该基准测试系统进行算例分析以进一步验证本文方法在系统侧谐波阻抗估计中的有效性，对该系统的具体参数设置详见文献［24］。在PCC处进行谐波数据收集，其11、13 次谐波电压和电流幅值的变化趋势分别如附录E 图E2、E3 所示，共采样5000个数据点。

分别采用4 种方法进行系统侧谐波阻抗估计，表2 给出了各方法的估计结果和相对估计误差。由表可见：方法1、2 受到背景谐波波动的影响，其估计结果与理论值偏离较远，估计性能较差；方法3、4 通过寻优计算得到最优阻抗初值，从而得到背景谐波电压值，并进一步分段估计以在背景谐波波动较大的场景下得到更接近理论值的系统侧谐波阻抗估计值；且与方法3 相比，方法4 直接在复数域进行系统侧谐波阻抗估计值计算，并利用改进自适应蝙蝠算法提高寻优性能，从而进一步提高了系统侧谐波阻抗估计精度；另外，方法4 在估计该基准测试系统PCC 处的11次和13次系统侧谐波阻抗值时，具有比其他3 种方法更高的估计精度。综上所述，该算例分析结果进一步验证了本文所提方法的有效性和适用性。

表2 基准测试系统PCC处系统侧谐波阻抗估计结果Table 2 Estimation results of system-side harmonic impedance at PCC of benchmark test system

3.4 实例分析

本节采用现场实测数据进行分析计算以验证本文所提方法的有效性。数据源自给某工业电弧炉供电的35 kV 母线（即PCC），采样频率为12 800 Hz。基于获得的实测录波数据，每秒采用快速傅里叶分解计算得到各次谐波数据。附录F 图F1 展现了其11 次谐波电压以及电流的幅值变化趋势，共采样3 000个数据点。

分别采用4 种方法对PCC 对应的系统侧谐波阻抗值进行滑窗迭代计算，滑动窗口大小为300 个数据点，计算结果如附录F 图F2 所示。由图可见，4 种方法计算得到的系统侧谐波阻抗估计值较为接近，具有较高的一致性。考虑到实际电网中的系统侧谐波阻抗在短时间内波动不大，可通过系统侧谐波阻抗估计结果的稳定性评价各方法的性能［16］。从图F2 可以看出，方法4 得到的系统侧谐波阻抗估计值曲线更为平稳。4 种方法的系统侧谐波阻抗估计值的方差如表3所示。由表可见，方法4的系统侧谐波阻抗估计结果具有最小的方差，由此可知，相比于其他3 种方法，本文所提方法的估计结果更为平稳。综上所述，实例分析结果证明了本文所提方法在实际工程应用中的适用性和有效性。

表3 4种方法的系统侧谐波阻抗估计值方差对比Table 3 Comparison of variance of system-side harmonic estimation value among four methods

4 结论

针对现有系统侧谐波阻抗估计方法对背景谐波波动敏感的问题，提出一种系统侧谐波阻抗估计新方法。该方法基于阻抗偏差最小判据，采用改进自适应蝙蝠算法迭代寻优得到最优阻抗初值，从而得到接近真实值的背景谐波电压值。通过对求得的背景谐波电压值进行聚类分析，将样本数据按照聚类结果分为多簇，从而减少每一簇数据的背景谐波波动水平。在此基础上，利用复最小二乘法求得更精确的系统侧谐波阻抗估值。算例分析结果表明，本文所提方法对背景谐波波动和两侧谐波阻抗比的变化具有更高的鲁棒性，所得系统侧谐波阻抗估计值与理论值更接近。

本文所提方法能有效估计系统谐波阻抗值的前提是系统谐波阻抗在分析时段内基本不变。当系统谐波阻抗值时变或发生大幅度突变场景下，如何进行准确的估计系统谐波阻抗，尚需进一步研究。

附录见本刊网络版（http：//www.epae.cn）。