基于数学核心素养对高考真题的深度探究
——以2022年新高考Ⅱ卷第22题为例
甘肃 刘延明
高考命题往往设置综合性的问题和较为复杂的情境,重视基于数学核心素养的关键能力的考查,而以函数、导数与数列不等式结合为载体的综合问题则是高考命题考查的重点和热点,往往处于解答题压轴题的位置.2022年新高考Ⅱ卷的第22题就是基于数学核心素养与关键能力考查的一道综合试题,该试题将函数、导数、数列与不等式等知识有机结合,考查学生灵活应用函数、不等式思想解决复杂问题的能力,对抽象概括能力和推理论证能力有较高的要求,无论是在数学知识层面、数学能力层面,还是在创新思维层面都很好地体现了基于数学核心素养与数学关键能力的考查.为此,本文以该试题为母题,从解法和变式等不同视角进行深度探究.
一、母题呈现
【例】(2022·新高考Ⅱ卷·22)已知函数f(x)=xeax-ex.
(1)当a=1时,讨论f(x)的单调性;
(2)当x>0时,f(x)<-1,求a的取值范围;
二、母题分析
该母题是以高考中高频次出现的基本函数“ex”为背景的导数应用试题,其中第(3)问是数列不等式的证明问题,解答这一小问的基本思路是:逆向“执果”分析,寻求与目标不等式等价的不等式→构造函数,由导数知识证明或推理得到函数的基础不等式结论→将结论通过赋值转换为数列的不等关系→运用数列中诸如裂项、累加等方法或结合“放缩法”的应用→数列不等式得以证明.
三、母题解答
(1)当a=1时,f(x)=xex-ex,所以f′(x)=(x+1)ex-ex=xex.
所以当x≥0时,f′(x)≥0;当x<0时,f′(x)<0,
故f(x)在[0,+∞)上单调递增,在(-∞,0)上单调递减.
(2)解法1:令g(x)=f(x)+1=xeax-ex+1(x>0),
则由f(x)<-1,得g(x)
又g′(x)=eax+axeax-ex,所以g′(0)=0.
令h(x)=g′(x)=eax+axeax-ex,
则h′(x)=aeax+a(eax+axeax)-ex,h′(0)=2a-1.

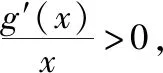




点评:解法1直接转化,构造函数,借助导数定义在分析和推理论证的基础上求解,落实了数学抽象、逻辑推理等数学核心素养.
解法2:由题意可知f′(x)=(1+ax)eax-ex,f′(0)=0.
令g(x)=f′(x)=(1+ax)eax-ex,则g′(x)=(2a+a2x)eax-ex,g′(0)=2a-1.
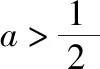
所以g(x) 在(0,x0)上单调递增,又g(0)=0,所以g(x)>0在(0,x0)上恒成立,


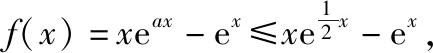
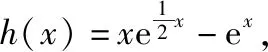
则h(0)=-1,



点评:解法2首先对函数求导,然后构造函数,借助“二阶”导数在分析和推理论证的基础上求解,落实了数学抽象、逻辑推理等数学核心素养.
(3)证法1(分析法):令Sn=ln(n+1),


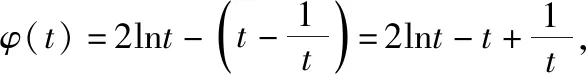
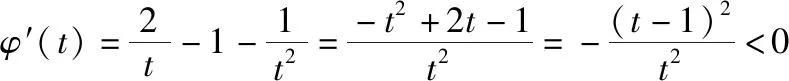
故不等式得证.
点评:证法1首先将所证数列不等式逆向分析、转化,发现其结构形式、特点,然后换元、构造函数,利用导数研究函数的单调性证明不等式结论,从而利用该不等式结论证得不等式.

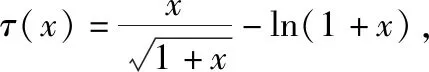

所以τ(x)在(0,+∞)上单调递增,所以当x>0时,τ(x)>τ(0)=0.
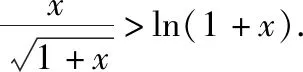
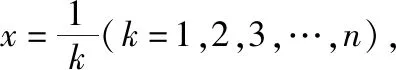
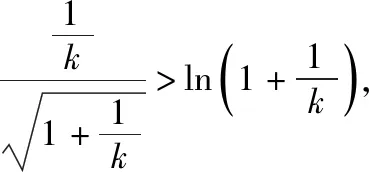


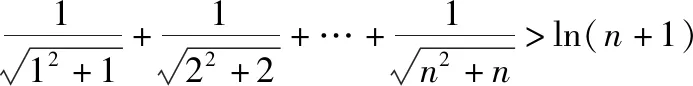

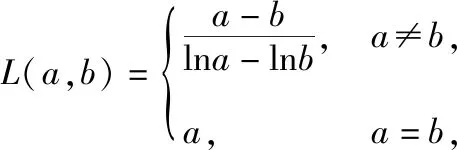
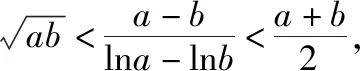

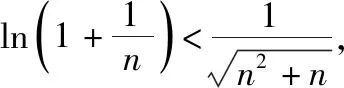
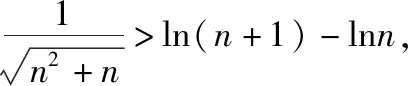

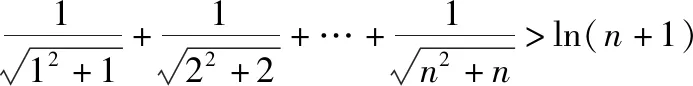
点评:证法3直接利用对数均值不等式来证明,过程简洁,十分巧妙.这里需要说明的是,在考试中对数均值不等式不可以直接应用,需要先进行证明.
四、考查模式
导数及其应用是高考考查的核心内容,其解答题常处于高考压轴题的位置.在导数及其应用解答题中融入数列不等式证明问题,不仅体现了高考命题知识间的交汇、综合,也使得“导数题”起到了高考“把关定向”的作用.在高考中,数列不等式的证明往往设置在导数及其应用解答题的最后一问考查,先由导数知识证明或推理得到函数的基础不等式结论,然后将结论通过赋值转换为数列的不等关系,再运用数列中如裂项、求和、累加等知识或方法并结合“放缩法”的应用,使得数列不等式得以证明.
五、母题变式
若只改变母题的题设中的函数形式,数列不等式不变,可有:
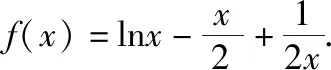
(1)解关于x的不等式f(x)>0;
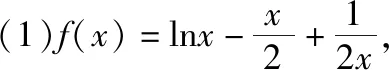
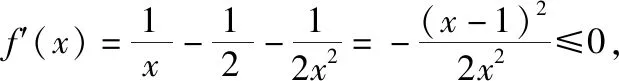
所以f(x)在(0,+∞)上单调递减.
又f(1)=0,所以f(x)>0的解集为(0,1).

当n≥2且n∈N*时,由(1)可知,


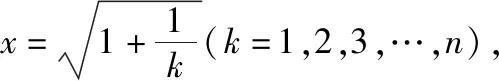

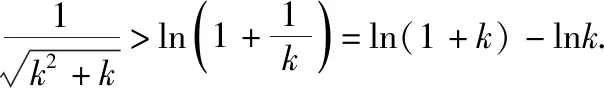
然后赋值、累加证得不等式,下同母题第(3)问证法2.
若母题的题设中的函数形式不变,改变第(3)问所证明的数列不等式,可有:
【变式2】已知函数f(x)=xeax-ex.
(1)当a=1时,讨论f(x)的单调性;
(2)当x>0时,f(x)<-1,求a的取值范围;
解析:(1),(2)见母题的解析.


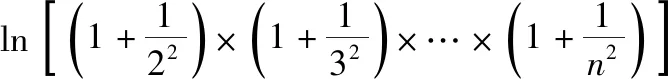
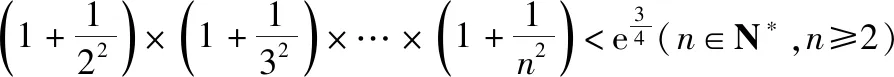
若母题的题设中的函数形式,深度改变第(3)问所证明的数列不等式,可有:
【变式3】已知函数f(x)=xeax-ex.
(1)当a=1时,讨论f(x)的单调性;
(2)当x>0时,f(x)<-1,求a的取值范围;

解析:第(1),(2)问解析见母题的解析.
(3)因为Sn=2n-1,
所以当n=1时,a1=S1=21-1=1,
当n≥2时,an=Sn-Sn-1=2n-1-(2n-1-1)=2n-1,当n=1时,等式成立.
故数列{an}的通项公式为an=2n-1.
所以bn=2(log2an+1)=2(log22n-1+1)=2(n-1+1)=2n,
证法1:从不等式左边式子是分式连乘积的形式等结构特点,联想到运用累乘法,首先研究、变形“通项”,然后运用累乘法来证明.
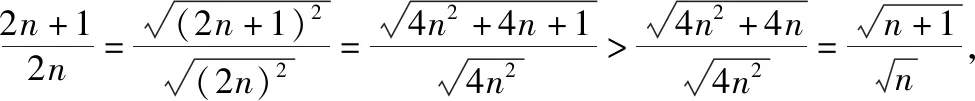
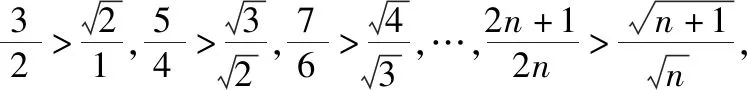
上述各式左、右两边分别相乘,得


点评:证法1由不等式左边式子的特点,联想累乘法,通过“放缩”变形左边连乘积的分式的“通项”,运用累乘法证得不等式.
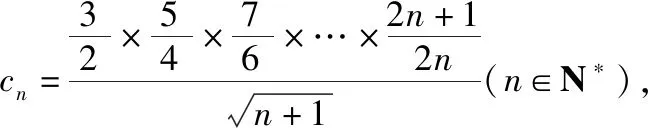
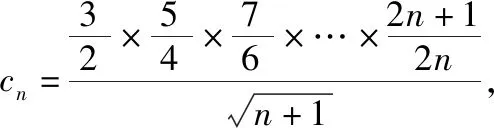
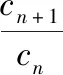
所以cn+1>cn,所以数列{cn}是单调递增数列.

所以cn>c1>1,


点评:证法2首先通过构造数列,推证数列的单调性,利用数列的单调性证明不等式成立.在推证不等式的过程中运用了“分母扩大,分式缩小”的放缩技巧,值得重视.
证法3:由于所证不等式是与正整数n有关的数列不等式,所以考虑运用数学归纳法来证明.
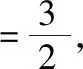
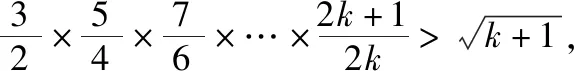
则当n=k+1(k∈N*)时,

所以当n=k+1时,不等式也成立.

点评:证法3运用数学归纳法证明不等式,思路清晰、自然,但有两点值得注意:一是由n=k时不等式成立,证明n=k+1时不等式也成立,务必要用归纳假设;二是在n=k+1在证明不等式时,用到配方、分离、放缩等代数式的变形技巧.
六、方法规律
通过上面母题和变式题的解析可以看出,解答函数、导数与数列不等式结合的综合问题的关键是数列不等式的证明,在证明数列不等式的过程中往往需要用到 “放缩法”.“放缩法”灵活多变、技巧性强,如何把握放缩的“度”,使得放缩“恰到好处”,这正是“放缩法”的精髓和关键所在.在解题中要多观察、分析、思考和体会,深入剖析问题特征,抓住规律进行恰当地放缩,从而顺利完成数列不等式的证明.在数列不等式证明时,用到的“放缩法”主要有:
1.裂项放缩证明数列不等式
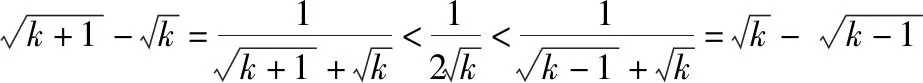
2.分式放缩证明数列不等式
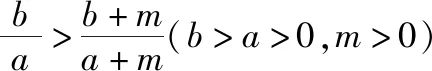
3.添舍项放缩证明不等式
根据数列不等式的特点,将数列不等式的一边添项或舍项进行放缩以达到解决问题的目的.如变式2.许多时候是多种方法共用,比如测试题或经过多次放缩后才能达到证明不等式的目的.
七、教学启示


