一种基于宽度学习的高精度光谱重建方法

杨艳红，万晓霞，薛智爽，刘段，邢海峰

（1.武汉大学 图像传播与印刷包装研究中心，武汉 430072；2.湖北广彩印刷有限公司，湖北广水 432721）

数码相机可以非常容易地获取被摄物体图像的RGB 响应值，但是获得的颜色与设备和光照条件相关，为了使颜色能够在不同的媒介间保真传递，需要使用更为精确的颜色表征方法。光谱反射率是决定物体颜色的本质属性，是一种更为准确的表征方法，获取到物体的光谱反射率，即可准确还原物体在不同光照和不同观察者条件下的真实颜色[1]。近年来，直接从数码相机响应值进行光谱重建的方法受到越来越多研究者的关注，它具有低成本、快响应、高分辨率等特点，而且可以有效避免光学带通滤波器多光谱系统中存在图像几何失真等的固有问题[2]，在遥感、电影电视、出版印刷、文物修复和艺术品研究、在线商品展示等多个领域都有广泛应用。

光谱重建算法是多光谱成像技术的核心。目前，基于训练样本的光谱重建方法已经成为基于数码相机光谱重建研究的主流方法，传统方法包括伪逆法、主成分分析法、核算法、回归法、R 矩阵法等[3]。Shen等[4]针对传统最小二乘法过拟合的问题，提出采用偏最小二乘法求解光谱估计矩阵的全局光谱重建算法，重建精度优于维纳估计和普通的多项式回归，但仍有很大的提高空间。Amiri 等[5]对全局加权形式的非线性回归方法进行了研究，虽然加权非线性回归方法光谱重建精度优于其他方法[6]，但是色度误差较大，需要解决，经测试得出不同加权形式对光谱重建的光谱精度和色度精度的影响不同，但整体精度还有待提高。随着计算机视觉技术的快速发展，基于深度学习的光谱重建技术逐渐得到关注和研究，在图像分类、目标识别和图像超分辨率等领域有重要应用。在NTIRE 2018 和NTIRE 2020 光谱重建挑战赛中，排名领先的从RGB 三通道图像进行光谱重建的方法都采用了基于深度学习的神经网络模型法来进行光谱重建[7-8]。此类方法对数据集提出了更大的需求，当数据规模庞大时，深度学习模型权重调整耗时，容易陷入局部最优解；而传统简单的神经网络在小数据集上应用时容易“过拟合”，使用小样本的此类方法的应用稳健性较差。

宽度学习系统（broad learning system，BLS）是在深度学习的快速发展和应用中应运而生的，相对于深度学习的多层复杂耦合结构，宽度学习通过特征映射和增强映射的方式在宽度上构造网络，结构更为精简，训练速度更快，且具有很好的特征提取和逼近能力，准确率高，适用于数据特征不多但对预测实时性要求较高的系统[9]。基于此，文中提出一种基于宽度学习的光谱重建算法，并采用十次十折交叉验证的实验方法，将文中所提算法（New）与Shen 的偏最小二乘算法（SHEN）以及Amiri 和Fairchild 的全局加权非线性回归算法（A-F）进行对比。为评估新方法的性能，分别计算光谱均方根误差和光谱拟合优度误差作为光谱精度评价指标，计算CIE DE1976 和CIE DE2000 作为色度精度评价指标。

1 原理

1.1 光谱重建基本原理

假设数码相机的光电转换函数为理想线性化模型，则其成像过程的数学模型可表示为式（1）[10]。

式中：d为一个像素点的K×1 维响应值向量；K为成像系统的通道数，对于三色数码相机来说，K=3；r为一个像素点的N×1 维光谱向量；M为包含了l(λ)、t(λ)、f i(λ)和s(λ)在内的K×N维系统整体灵敏度函数矩阵。光谱重建算法实质就是实现上述成像模型的反向求解，具体如式（3）所示，即实现由多通道响应信号d到对应光谱信息r的计算，确保对于给定的任意三维通道响应值d，均能重建得到其对应光谱数据r，其中f( )代表光谱重建所采用的具体方法。

1.2 基于宽度学习的光谱重建算法

基于BLS 的光谱重建方法的整体设计思路为：首先，将数码相机获得的三维响应值进行多项式拓展，为了提升重建的精度，大多方法通常会采用多项式拓展项数的方法，这种方法已在很多研究中被证实是有效的[11]。然后，将拓展后的设备响应值作为输入数据，通过一些特征映射和稀疏表示转化为随机特征，作为网络的特征节点，这些特征节点通过非线性激活函数进一步连接，形成增强节点。最后，所有映射的特征和增强节点直接连接到输出端，即训练样本的光谱矩阵，其中该输出层的权重将通过系统方程的快速伪逆或迭代梯度下降训练算法来确定[12]，训练过程见图1。测试过程只需按步骤直接应用训练好的权重矩阵即可通过设备响应值预测出其真实的光谱反射率，下面是基于BLS 的光谱重建方法的详细描述，网络结构见图1。

图1 基于宽度学习的光谱重建网络结构图Fig.1 Framework of spectral reconstruction network based on BLS

式中：Wm为连接特征节点和增强节点层与输出层的权重。这里使用岭回归近似可以计算得出：

由此得到整个网络的权重Wm。

最后测试样本的响应值作为输入，通过训练好的权重生成相应节点即可估计出重建的光谱反射率，公式为：

2 实验与分析

本研究采用广泛应用于彩色成像设备颜色特性化的多项式模型作为相机响应值拓展的参考模型，d经多项式模型扩展为dex，样本集输入为N个拓展响应值的集合，矩阵表示为：

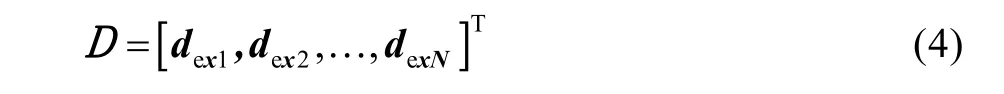
生成特征节点。对拓展后的响应值进行特征映射，对于n个特征映射，每个映射生成k个节点，用方程形式可以表示为：

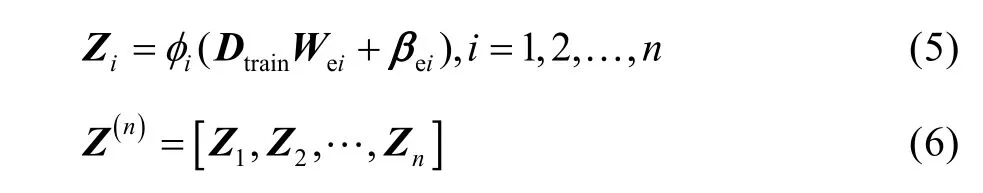
式中：Zi为特征节点，且Zi∈RN×k；Wei和βei分别是随机产生的权重系数矩阵和偏置向量；Z(n)为n个Zi串联成的矩阵。为了获得输入数据的稀疏表示，减少新生成特征节点的线性相关程度，使得新生成的节点不至于过于“浪费”，可通过线性反向最优化求解对随机初始化的权重矩阵Wei进行微调[13]，公式为：

2.1 实验设置

模拟实验采用孟塞尔亚光彩色谱（Munsell matt colors，MMC）数据集和Agfa IT8.7/2 （IT8.2）数据集[14]。 MMC 数 据 集 是 由 Jouni Hiltunen 用Perkin-Elmer lambda 9 UV/VIS/NIR 分光光度计从孟塞尔彩色亚光图集的1 269 块色块上测量的，测量了380～800 nm 的光谱数据，采样间隔为1 nm。IT8.2数据集是根据IT8.7 标准设计的，由Elzbieta Marszalec 用Minolta 分光光度计CM-2002 测得，测量了289 个色块400～700 nm 的光谱数据，以10 nm 为间隔。实验中为了统一取样范围和间隔，在MMC 中同样取出400～700 nm 范围，采样间隔为10 nm 的数据。CIE L*a*b*色度图中2 个光谱数据集的色度坐标见图2，由CIE 1931 标准观察者和CIE D65 标准照明体计算得出。

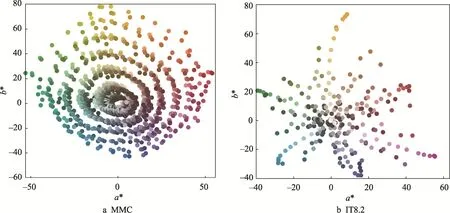
图2 数据集的色度坐标分布Fig.2 Chromaticity coordinates distributions of datasets

基于式（2）中的成像模型，忽略真实相机系统的非线性因素，对数据集的相机响应进行了模拟。模拟成像装置采用Nikon D7200 相机传感器的光谱灵敏度函数，光源采用CIE 标准光源D65，相机光谱灵敏度函数和光源的光谱分布如图3。彩色数码相机的响应值通常是三维的，表示为[r g b]，在实验过程中，我们发现仅仅是三维重建，宽度学习系统重建的效果并不理想，而将响应值拓展为二阶项数之后，重建效果则明显加强，重建为三阶则几乎不再提升，故本研究选择二阶多项式模型[1 r g b rg rb gb r2 g2 b2]来处理输入数据。由于宽度学习系统的训练过程中需要寻找随机系数矩阵，可能会导致测试结果的微小差异，为了更可靠、更公平地测试模型，使用了十次十折交叉验证的实验方法来评估所提出的方法。将MMC 样本集和IT8.2 样本集分别随机划分为大约10 个大小相等的子集，在这10 个子集中，一个子集被保留为测试模型的验证数据，其余9 个子集被用作每个折叠测试的训练数据，相当于每个样本随机划分循环验证了100 次，计算100 次测试指标的平均数参与最终的对比评价[15]。

图3 整体系统光谱灵敏度函数Fig.3 Spectral sensitivity functions of the whole system

2.2 结果与分析

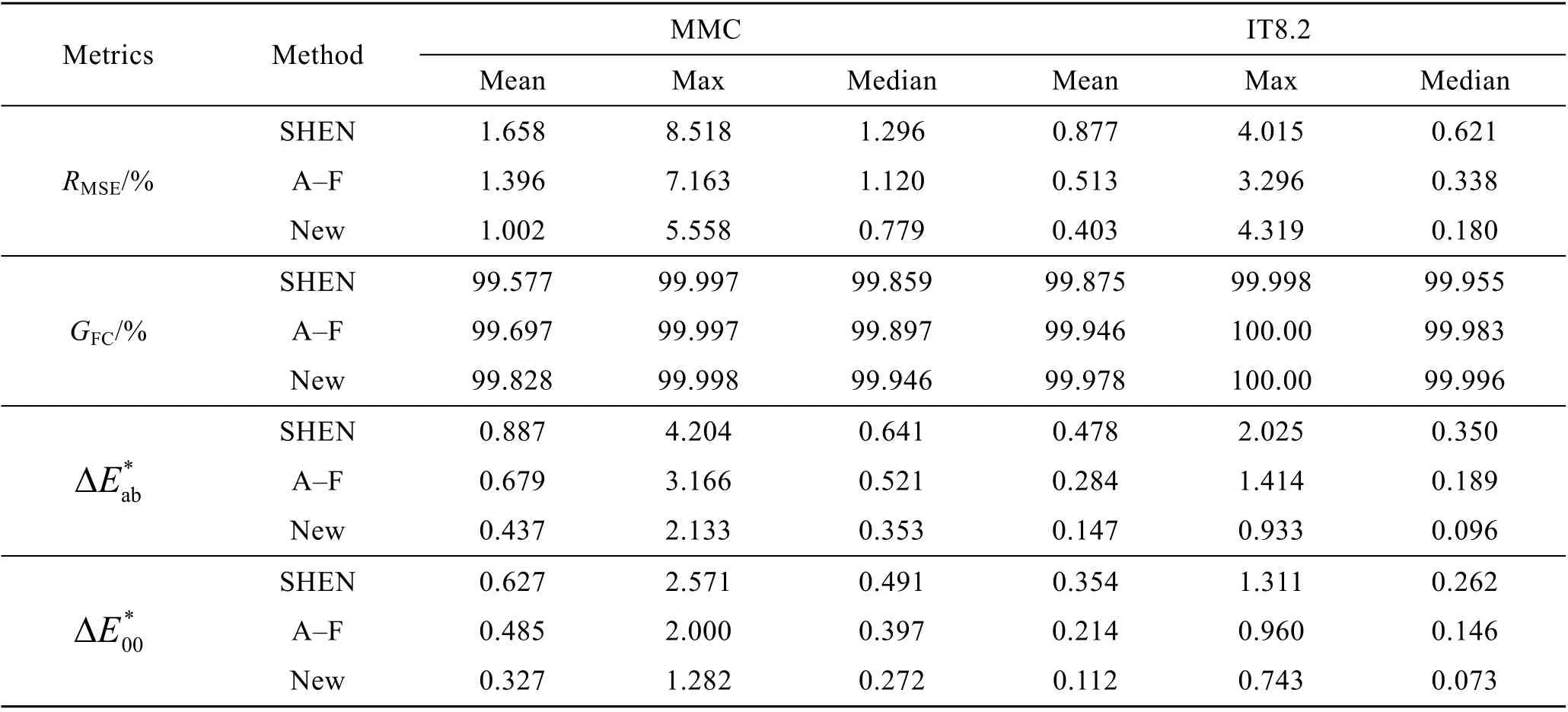
表1 2 种样本在不同算法下的光谱重建精度比较Tab.1 Comparison of spectral reconstruction precision between 2 different samples under different algorithms

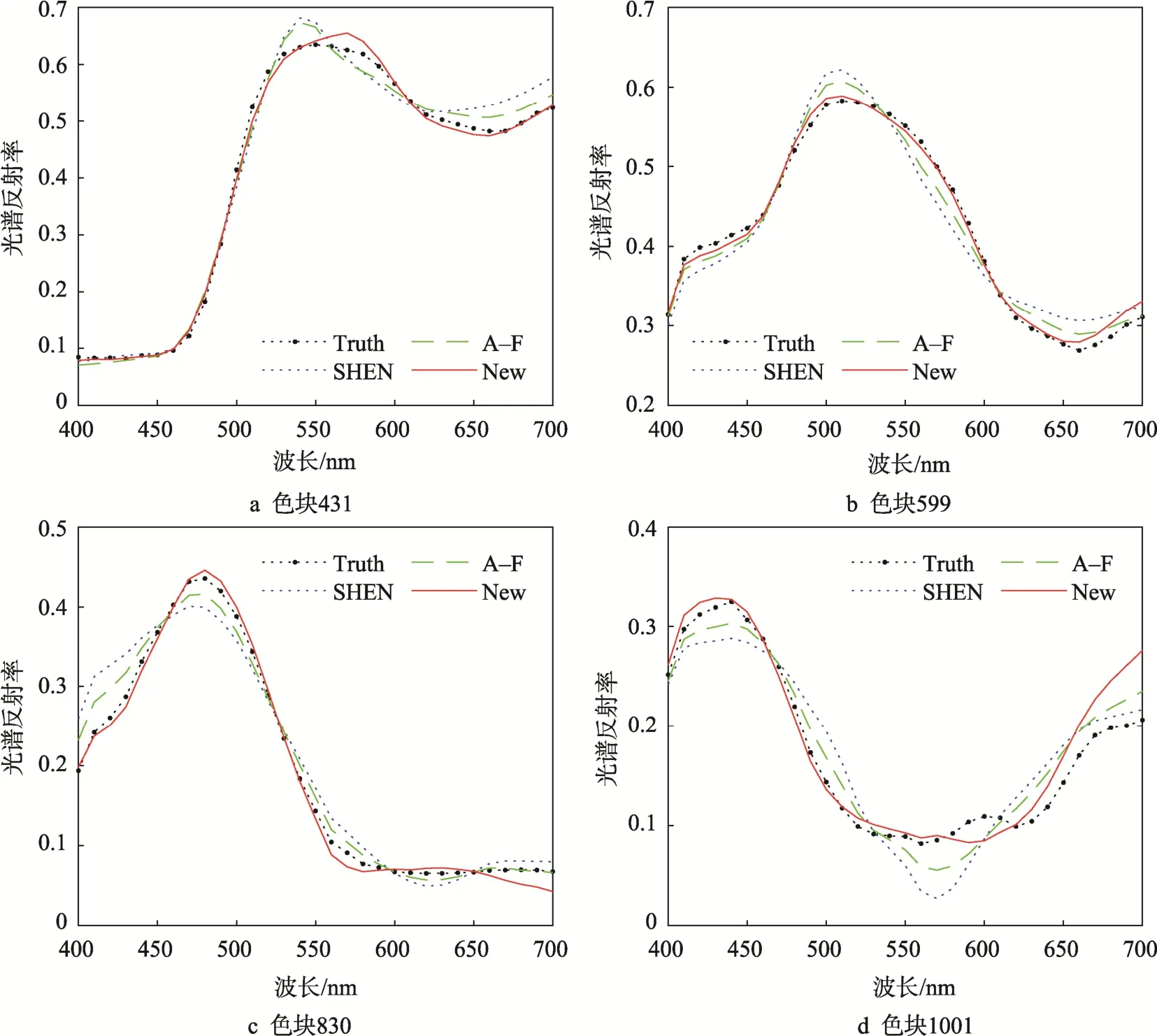
图4 MMC 中部分测试样本3 种方法光谱重建拟合曲线Fig.4 Spectral reconstruction fitting curves of some test samples in MMC by 3 methods

3 结语

文中针对数码相机的多光谱成像技术，将宽度学习系统应用于光谱重建，在重建的过程中采取了多项式拓展的方式以适应于宽度学习系统，提出一种新的全局训练的光谱重建方法。该方法网络结构简单，训练速度快，准确率高，重建结果在光谱精度和色度精度上都取得了较好的效果。与2 种现有的基于全局训练的方法相比，文中方法的重建效果无论是在光谱误差还是色度误差方面都表现更佳，说明宽度学习系统在相对较少的训练样本的学习下，可以很好地适用于光谱反射率重建，在数码相机的光谱成像领域有很好的应用前景。