射频SAW器件非线性信号的测量及产生机制分析

李百川，罗 阳，傅肃磊，王为标，张巧珍

(1.上海师范大学 信息与机电工程学院，上海 200234；2.清华大学 材料学院，北京 100084；3.无锡市好达电子股份有限公司，江苏 无锡 214124)

0 引言

声表面波(SAW)双工器作为射频前端的关键组件，被大量生产并广泛应用于移动通信系统。第五代移动通信技术(5G)应用中的多频带和高功率问题，对射频前端的封装体积和功率耐受提出了更严苛的要求。射频前端的高度集成和高能量密度使SAW器件的非线性问题愈发严重。一方面，发射(Tx)信道产生的非线性谐波信号会对相邻频带的接收(Rx)信道形成干扰；另一方面，Tx信号与天线(ANT)传入的干扰信号之间会发生互调失真(IMD)，严重恶化信号接收灵敏度[1]。因此，研究非线性信号的产生机理和抑制方法，对提高SAW器件线性度具有重要意义。

将理论仿真与实验测量结合是研究非线性产生机制及其抑制的重要途径。经典的SAW器件理论分析工具包括等效电路、耦合模(COM)和P矩阵等[2]，很多学者借助此类方法对常规SAW器件的非线性进行了建模分析。Chen等[3]使用梅森(Mason)等效电路模型计算了SAW双工器中的三阶非线性失真。Nakagawa等[4]建立了SAW谐振器的非线性COM模型，并使用该模型分析了常规SAW谐振器中多种非线性产生机制对三阶非线性信号产生的贡献。Chauhan等[5]将其拓展为P矩阵形式，用于分析温度补偿型SAW(TC-SAW)器件的非线性。然而，近年来涌现了大量的多层复合薄膜结构SAW器件，例如村田提出的IHP SAW器件，该类层状器件中存在复杂的多界面边界条件和材料组合，上述3种方法难以精确求解此类器件的非线性响应。因此，许多学者使用更具通用性的有限元方法(FEM)研究SAW器件的非线性[6-8]。

实验测量方面，Gawasawa等[9]和Solal等[10]分别测量了常规SAW和TC-SAW器件的非线性信号，而国内尚未见相关报道。因此，本文设计搭建了SAW器件的非线性测量系统，对不同结构SAW谐振器的二次谐波(H2)和三次谐波(H3)信号进行测量；讨论了非线性谐波的两种产生机制，通过非线性FEM模型[11]仿真并与测量结果进行对比，验证了其对谐波产生的贡献。

1 非线性测量系统设置

1.1 测量系统

本文搭建的SAW谐振器谐波测量系统示意图如图1所示。图中，信号发生器(SG)产生的连续波(CW)信号经功率放大器(PA)放大后，通过同向双工器1(Diplexer)低通带送入待测器件(DUT)，在工作频率范围激励DUT。DUT产生的二次、三次谐波信号经过同向双工器2高通带和高通滤波器(HPF)后，由频谱分析仪(SA)在对应频率范围进行观测。由于SAW器件的非线性信号十分微弱，为了实现对其准确有效的测量，必须选择高线性度的SG和SA，以减少测量系统自身非线性的对测量的干扰。此外，DUT两端的阻抗匹配也是测量系统设置的关键考虑因素。

图1 SAW谐振器谐波测量系统示意图

DUT端口1处的CW输入信号功率设置为+15 dBm。图1所示测量系统使用定向耦合器、功率传感器和功率计进行功率监控，以确保测量全过程中DUT输入功率恒定。测量系统中DUT、同向双工器和高通滤波器均为频率选择性器件，在其各自的通带外存在阻抗失配。因此，在DUT的两个端口插入衰减器可以改善测量系统的阻抗匹配情况。此外，衰减器的插入能够抑制PA端自生谐波信号以及来自HPF端高频信号的反射，提高了测量系统线性度。

为消除SG和PA自身产生的非线性信号对测量的干扰，在SG和DUT端口1之间接入同向双工器1，使用其低通带滤除高频非线性信号。同理，在DUT端口2和SA之间接入同向双工器2。同向双工器2高通带和HPF的级联可以提供更好的带外抑制，提高系统测量灵敏度。另外，同向双工器1高通带和同向双工器2低通带与终端负载连接，这不仅可以吸收射频反射和泄漏，而且能使DUT两端阻抗在带内外保持50 Ω良好匹配。

1.2 待测SAW器件

待测器件选用衬底为42°YXLiTaO3(42-LT)的常规SAW谐振器，其具体结构参数如表1所示。为了对比不同工作频率的SAW器件非线性，本文对两个不同波长(λ)的谐振器进行测量。其中，谐振器1(R1)和谐振器2(R2)的波长分别为5.33 μm和5.81 μm。

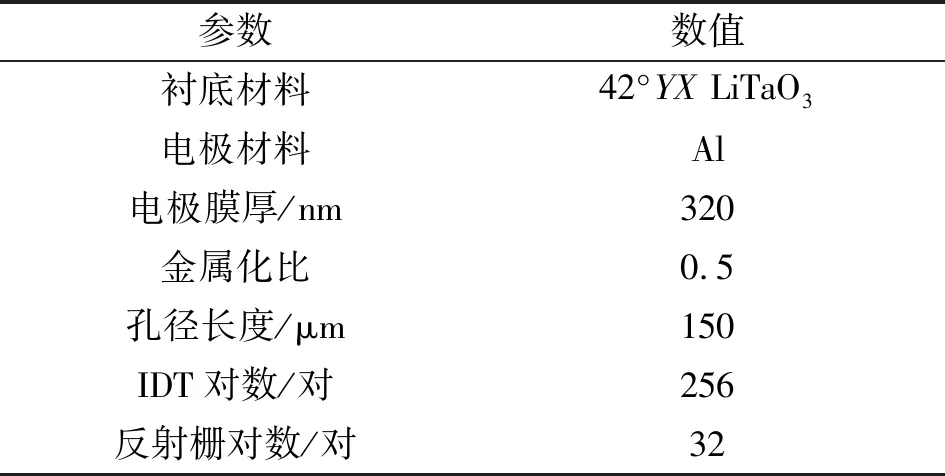
表1 待测SAW谐振器的结构参数

使用带有SMA接头的印刷电路板(PCB)将谐振器与其微带线串联，接入测量系统。R1和R2的回波损耗S11和插入损耗S21在矢量网络分析仪上测量的结果分别如图2(a)、(b)所示。由图可见，R1的谐振频率(fr)和反谐振频率(fa)分别为759.5 MHz和773 MHz；R2的fr和fa分别为697.5 MHz和710 MHz。R1和R2在频率略高于fa处存在寄生模式，其出现频率fsp分别约为783 MHz和717.5 MHz。

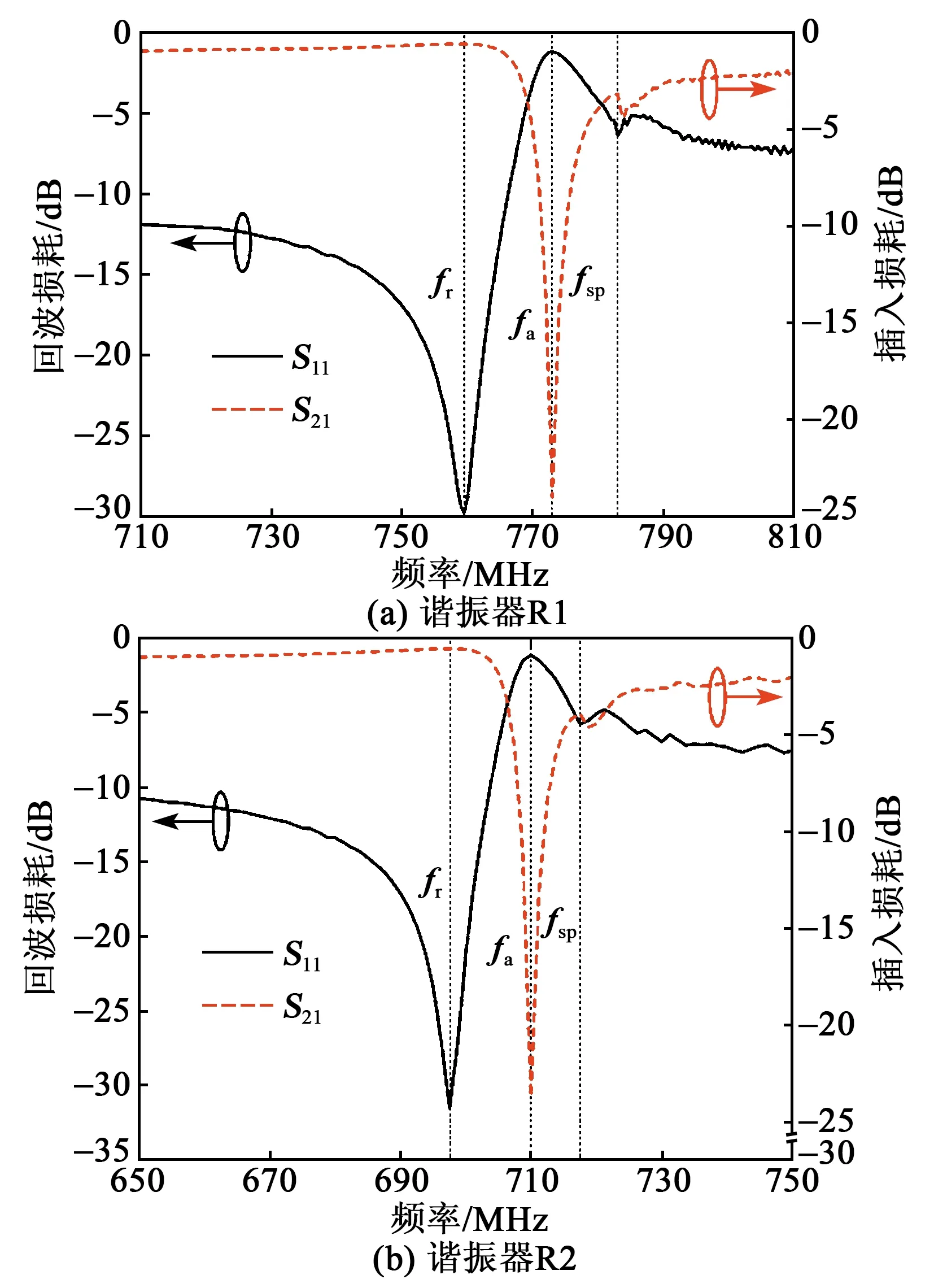
图2 S参数测量结果

2 测量结果与讨论

本文使用图1非线性测量系统对DUT的二次、三次谐波信号进行测量。测量中，SG频率扫描设置如表2所示。SG产生输入频率为f1和f2的CW信号分别用于激励R1和R2。扫频中心保持在fr和fa附近，以确保谐振器在工作频率范围产生的非线性信号的频率特性可被SA在对应输出频率范围完整地测量。

表2 谐波测量扫描频率设置

2.1 二次谐波测量

图3为两个谐振器H2信号的测量结果。如图3(a)所示，R1的二次谐波响应在其输出频率(2f1)范围整体呈缓慢下降趋势，最大值出现在远离谐振频率fr的低频处。H2两个连续的谷值分别出现在略低于谐振频率fr和寄生模式fsp处，一个峰值在略低于反谐振频率fa处。如图3(b)所示，R2的二次谐波响应在其输出频率(2f2)范围同样呈下降趋势，两个谷值分别在略高于fr和fsp处，峰值出现在fa附近。

图3 二次谐波测量结果

使用与R1、R2相同规格的谐振器进行重复实验，其测量结果与图3一致。该步骤排除了测量系统自身非线性对测量的影响，同时消除了单次实验的偶然误差。因此，图3所示的H2频率特性是谐振器R1和R2固有的。

2.2 三次谐波测量

图4为R1、R2两个谐振器的三次谐波信号测量结果，这两个谐振器三次谐波的输出频率分别是其输入频率的三倍频3f1和3f2。如图4(a)所示，R1的H3曲线峰值出现在fr处，随后其幅度快速衰减约30 dB，在频率略低于fa和fsp处形成两个邻近的下凹尖峰。如图4(b)所示，R2的H3曲线频率特性与R1相似，H3在fr附近达到峰值，随后分别在fa和fsp附近陡峭下降，形成两个下凹的尖峰。在两个谐振器H3测量结果中，下凹尖峰处的谷值与测量系统非线性背景水平(约-135 dBm)接近，需要以更小的扫频步进在fa和fsp附近进行重复测量，以便排除背景噪声的干扰。重复测量的尖峰频率和幅值与图4差异微小，表明图4中H3曲线的频率特性是两个测试谐振器固有的。

图4 三次谐波测量结果

2.3 谐波产生机制分析

非线性谐波的产生机制可以借助非线性压电本构方程进行分析。基于微扰理论，非线性压电本构方程[11]可表示为

T=cES-eE+TN

(1)

D=eS+εSE+DN

(2)

式中：T,D,S和E分别为应力、电位移、应变和电场；cE,e,εS分别为线性弹性常数、压电常数和介电常数。非线性应力TN和非线性电位移DN作为微扰项，可表示为S和E的非线性组合：

(3)

(4)

式中χij为非线性系数，下标i与j的和为其对应的非线性阶数。

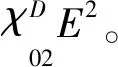
图5 谐振器R1的三次谐波仿真与测量拟合结果

3 结束语

本文搭建了SAW器件的非线性测量系统，对42-LT衬底上两个常规SAW谐振器的二次谐波和三次谐波信号进行了测量。通过分析测量结果，对非线性谐波的主要来源进行了讨论。对比测量与FEM仿真结果，验证了介电非线性和声应变非线性效应对谐波产生的贡献。本文所搭建测量系统的非线性背景水平低于-135 dBm，可以灵敏地测量非线性谐波信号。本文结合非线性的理论仿真与实验测量，为探究SAW器件非线性的产生机制和抑制方法提供了思路。后续工作将考虑进一步加强测量系统的可靠性，尝试拓展测量系统以实现对包括互调失真信号等各类非线性信号的准确测量，更加全面和深入地研究SAW器件的非线性产生机理，探究有效的非线性抑制方法。