迭代逼近法偏角摄影校正技术

樊少勇 王梓入 包 清,2

（上海市公安局刑事侦查总队 上海 200083 ；上海理工大学光电信息与计算机工程学院 上海 200093）

1 引言

传统物证摄影中，一般都要求相机镜头垂直于痕迹物证所在平面，即使有偏差，但不能超过5度。但实际案件的现场勘查中，尤其是一些疑难痕迹物证的提取过程中，采用偏角摄影的方法提取痕迹物证存在不可忽视的价值。一是痕迹物证受到场景制约不便于垂直提取；二是一些疑难物证的拍照提取中存在最佳偏角，使得痕迹和承痕体的反差最佳，当痕迹物证和承痕体反差较小时，只有在最佳偏角附近才能提取到高反差和较高质量的图像。由于偏角拍摄的影响，痕迹物证图像的变形不可避免，尤其是在大偏角提取时图像变形大，严重影响了后续的检验鉴定。为使偏角摄影图像能够很好地应用于检验，图像校正变得至关重要[1-2]。本文在包清[3]等人的校正方法基础上，利用迭代逼近法的校正技术，对8组偏角摄影提取图像校正开展比较实验，所提出的方法均优于比较方法。

2 偏角摄影校正技术现状

偏角摄影图像校正的方法主要分为两大类，一是物理校正法，利用光路的可逆性对偏角提取的图像进行校正。该方法需要额外的设备，还会受到操作人员的经验和主观影响[4-6]。二是软件校正法，通过相应的算法对图像的变形进行估计和消除。软件校正法是目前主流的校正方法。

李克伟[7]等人提出了对图像中的特殊标识复原的图像校正技术，但是该方法校正效果一般，尤其是在远离标识物时效果不佳。宋超[8]提出了构建标准图像与变形图像之间的函数关系，利用插值技术校正图像的方法，该方法缺少在大偏角提取条件下校正后的实证。孙雯[9]等人提出了一种改进的透视变换算法，该方法只考虑了投影形变，没有考虑到透镜组在偏角提取时的非线性形变，因此，在校正非线性形变的偏角图像时效果不佳。王道累[10]等人提出了一种利用棱镜多目视图的校正方法，该方法校正效果较好，但需要多目立体视图，不适用于现场勘查中提取到的偏角物证图像的校正。杜召斌[11]等人提出了一种基于透视消失线的方法，通过对一组正交的消失线的校正达到校正变形图像的目的，该方法计算量大，需要记录和测量的参数多，并且需要特定的参考线，无法应用于当前的现场勘查实际。田利文[12]提出的基于霍夫直线检测的透视变换算法，该方法通常应用于校正有明显文字行文档，主要包含了平移变换、仿射变换等线性校正方法，该方法对大偏角提取的图像效果不佳。管海兵[13]提出了基于投影法的校正策略，通过在一组正交方向上的小角度旋转引起的投影变化进行校正，该方法精度依赖于单次旋转角度，为了压缩误差需要将单次的旋转角度控制得很小，图像校正的计算量过大。王垒[14]等人提出了一种基于点阵坐标的非线性手印校正方法，但该方法需要建立特征点之间的对应关系，在校正非线性变形的指纹中取得了良好的效果，应用于鞋印校正时，估计的畸变场误差较大。上述校正方法在应用于犯罪现场勘查中提取痕迹物证时，均存在实用性差的问题。

包清[3]等人提出了一种基于泰勒展开的双线性插值校正算法，该方法实操性强，在针对大偏角提取的鞋印校正中取得了良好的效果，但是该方法在校正过程中仅选取了两个标记点，对于图像的变形信息没有充分利用，本文正是在其基础之上提出了一种迭代逼近的校正技术，在保留其实践性强适用于现场勘查的同时，缩小了校正误差。

3 实验原理与方法

3.1 实验原理

使用偏角摄影方法提取固定痕迹物证时，产生变形的原因如图1所示，其中dl1为原物长度，θ为偏角角度，dl2为投影长度，x为物点到焦平面的偏移量，L2为焦距，f像为像距，dl3为投影长度的成像结果，dl4为原物长度的成像结果。造成图像形变主要是两种形变叠加后的结果：一是投影而造成的缩放，使得图像沿着某一方向各处均等的线性形变。二是痕迹物证距离焦平面的位置不同而导致的放大率的不同，使得图像沿着某一方向各处不同的非线性形变。

图1 形变示意图

包清[3]等人提出的校正方法虽然具备可操作性强校正效果良好的优点，但依然存在一些缺陷，主要体现在三个方面，一是校正过程中仅测量两个标识点，对形变图像的畸变场估计过于简化，存在误差较大的问题，如图2所示。二是为防止高阶参数过于敏感的问题，防止在远离焦平面处出现明显的“过校正”现象，在泰勒展开的过程中只是采用了二阶展开，导致了在远离焦平面时校正可能会存在较大的偏差，如图3所示。三是泰勒展开中的偏移量在偏角图像中是形变后的累积结果而不是标准的偏移焦平面的偏移量，偏移量与物点到焦平面之间的距离不为线性关系，如图4所示。本文提出的结合迭代逼近的泰勒二阶展开双线性插值校正方法，通过迭代法，在缩小校正误差的同时保留了原先校正方法可操作性强的优点。

图2 包清等人的校正方法示意图

图3 校正图像边缘可能存在较大误差

图4 偏移量与物点到焦平面之间的距离不为线性关系

依据包清[3]等人的校正方法，泰勒展开如式1所示，应用迭代逼近法调整后，展开如式2所示。

在迭代的过程中参照包清等人[3]的方法，每迭代一次就重新取两个标识点进行计算，选取的规则为初始标识点靠近中性线，随着迭代次数的增加标识点的选取逐渐远离中性线。通过多次选取标识点可以降低单次选取的误差对校正效果的影响，而依照距离中性线由近至远地选取标识点迭代，则在保留校正方法限制条件少可操作性强的基础上，对图像不同区域的畸变场的估计更充分、更准确。本文校正方法的伪代码如图5所示。应用迭代逼近法的校正图例如图6所示，从左至右依次为每一次的迭代结果，最右侧为最终校正结果。

图5 校正算法伪代码

图6 迭代逼近法示意图

3.2 实验方法

在光滑的瓷砖地面上遗留4个灰尘鞋印，参照现场勘查中鞋印提取的方法，采用掠入式的配光方式并放置比例尺进行光学拍照提取，拍摄的角度分别为垂直拍摄、偏角30度拍摄、偏角45度拍摄，如图7～10所示。

图7 鞋印1

图8 鞋印2

图9 鞋印3

图10 鞋印4

对鞋印1～4中偏角提取的图像分别采取通用图像处理软件Ps、包清[3]等人的方法、本文方法分别校正。在垂直拍摄的鞋印1～4中测量鞋印的长、宽，同时选取8个稳定可靠的特征点分别标记为a～h，按顺序连接上述8个特征点形成7个特征点之间的距离，共计9个指标，如图11所示。

图11 鞋印1～4特征点标注示意图

使用上述不同方法对偏角拍摄的图像进行校正，在校正图像中选取并测量相同特征点之间的距离，以该组数据与垂直提取图像中测量得到的数据进行比较，衡量不同方法之间的校正效果。

4 实验结果和讨论

4.1 实验结果

对实验中偏角拍摄的变形鞋印图像校正后的结果记录如表1～8所示，校正图像结果如图12～19所示。

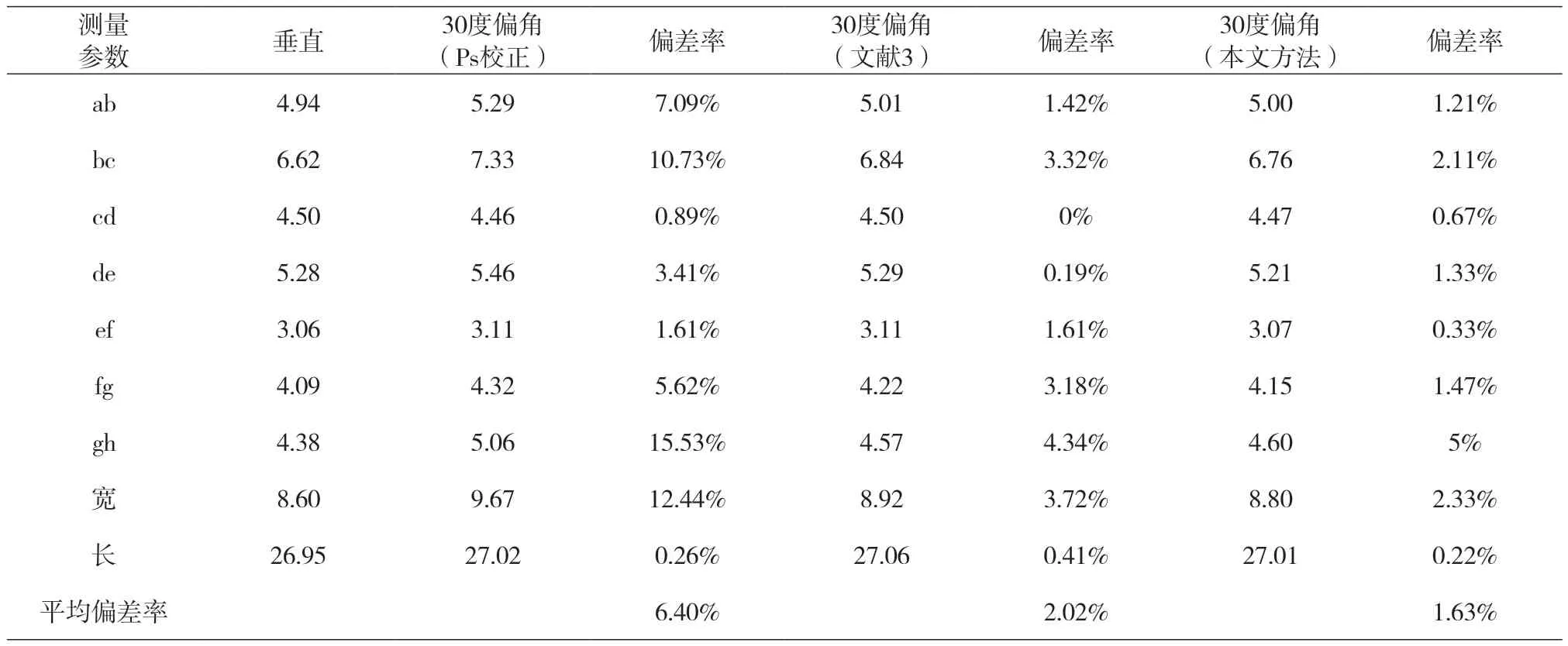
表1 30度偏角提取鞋印1图像校正比较结果

表2 30度偏角提取鞋印2图像校正比较结果

表3 30度偏角提取鞋印3图像校正比较结果

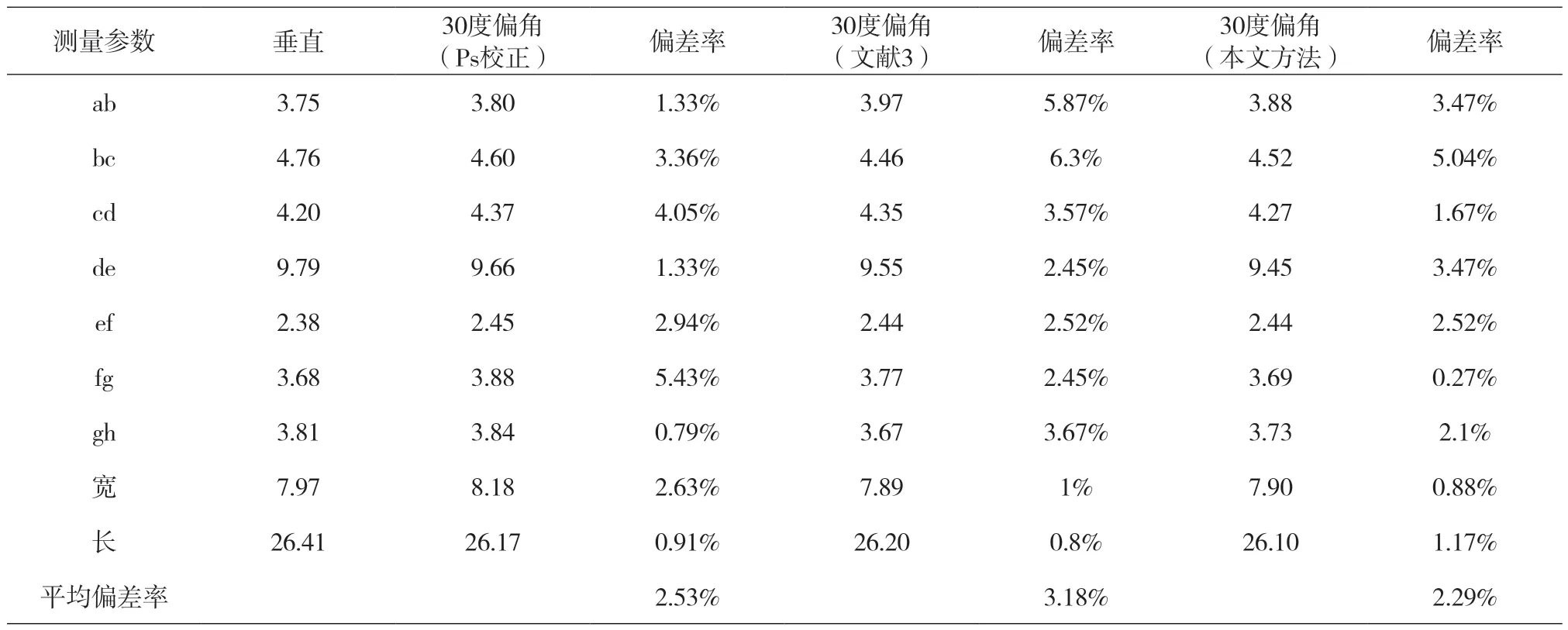
表4 30度偏角提取鞋印4图像校正比较结果

表5 45度偏角提取鞋印1图像校正比较结果

表6 45度偏角提取鞋印2图像校正比较结果

表7 45度偏角提取鞋印3图像校正比较结果

表8 45度偏角提取鞋印4图像校正比较结果

图12 鞋印1 -30度校正比较结果

图13 鞋印2-30度校正比较结果

图14 鞋印3-30度校正比较结果

图15 鞋印4-30度校正比较结果

图16 鞋印1-45度校正比较结果

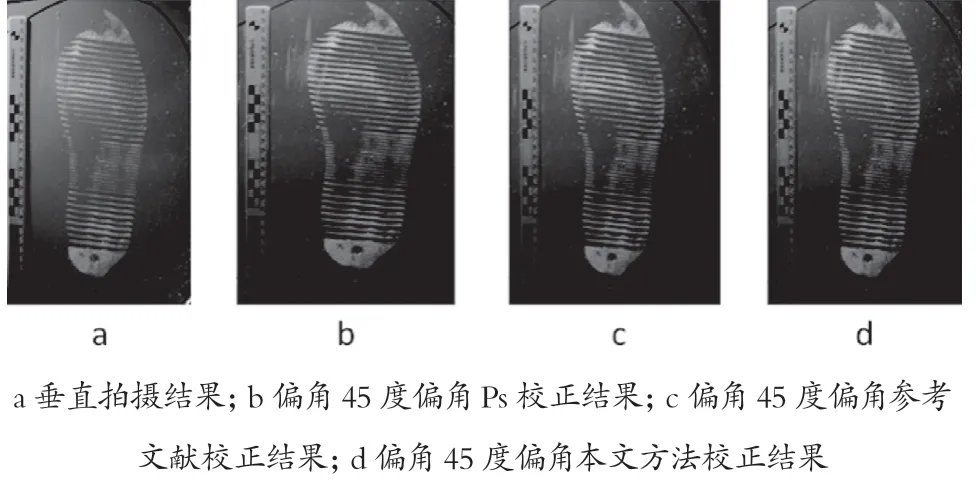
图17 鞋印2-45度校正比较结果

图18 鞋印3-45度校正比较结果

图19 鞋印4-45度校正比较结果

4.2 实验讨论

在4枚8组变形鞋印的校正实验中，本文方法的校正效果在平均误差及最大误差的指标上均显著优于Ps方法及参考文献方法。Ps方法与其他两种方法相比对操作人员的主观经验依赖很大，对畸变场的校正依靠人工估计缺乏客观可靠的依据，存在平均误差和最大误差偏大等问题。参考文献方法限制条件少，操作简便，有着良好的校正效果。但是，仍然存在着平均误差较大，在远离焦平面处校正误差大等问题。

本文的方法与参考文献方法相比，既保留了限制条件少、操作简便的优势，又通过迭代逼近法更准确地估计了偏角提取图像的畸变场，缩小了平均误差和最大误差。通过对实验结果的比较可以发现30度偏角提取的鞋印3校正后的误差相对较大。可能是由于在偏角拍摄时对焦位置明显偏离了画面中心，使得图像上半部分的大块区域距离焦平面距离远所导致，如图20所示。为保证本文校正方法能够取得良好的效果，在使用偏角拍摄的方法提取痕迹物证图像时，对焦位置应选择在画面中心附近。

图20 鞋印3-30度偏角拍摄鞋印中性线明显偏离画面中心

5 结论

使用迭代逼近法优化的基于泰勒展开的双线性插值图像校正技术具有校正效果好、限制条件少、实操性强等优势，适用于现场勘查中偏角摄影技术提取到的痕迹物证图像的校正。使得痕迹物证的光学提取不再局限于垂直方向拍照提取，较好地解决了受场景制约、痕迹和载体之间反差太小等疑难痕迹物证提取的情况。该方法丰富了物证摄影中图像校正的技术体系，显著提升了现场勘查中疑难痕迹物证的提取率和利用率。