“任意角”概念不同引入方式的比较研究
孙信玲
(江苏省南京市建邺高级中学 210019)
教师普遍认为“任意角”这一节的内容难度不大,在教学中很容易处理.在初中,学生学习过“角”的概念,是0°~360°范围的角.教师通过生活情境的引入,让学生感受现实生活中随处可见超过0°~360°范围的角,比如跳水中的“翻腾三周半”、体操中的“前空翻转体720°”、车轮旋转两圈等.然后教师逐一介绍关于角的概念的相关规定,包括角的定义、角的始边与终边、角的正负、终边相同的角等,于是完成了角的扩充.
然而,“任意角”这一节作为《三角函数》这个章节的章首课,担负重要的功能,在大单元视域下,将这节课与全章内容联系,可以发挥其更大的作用.同时,“任意角”作为一节概念课,是“角的概念”的扩充,知识点比较多且散,应具有其合适的教学规律与方法.
1 三种不同的“任意角”概念的引入方式
在本学期的南京市公开课中,开设的三节课设计了不同的概念引入方式,笔者参与了研究过程,也进行了学习思考,现将三种不同的概念引入方式记录与分析如下.
1.1 教学设计A
问题1在初中阶段我们学习过角,它是如何定义的?你认识哪些角?
设计意图在初中阶段,角的定义是:具有公共端点的两条射线组成的图形叫做角.这个公共端点叫做角的顶点,这两条射线叫做角的两条边.这是角的静态定义.初中教材中也介绍了角的动态定义:角也可以看成是一条射线绕着它的端点旋转到另一个位置所成的图形.学生已经学习过的角是锐角、直角、钝角、平角、周角,角的范围是0°~360°.这既是复习旧知,也是为角的扩充作准备.需要说明的是,高中教师往往认为初中只讲了角的静态定义,高中的重点是将角的概念推广到“旋转成角”以及扩大范围.其实在初中已经介绍了角的动态定义,高中推广的是角的旋转量和旋转方向.
问题2(1)游乐园中的摩天轮旋转了两周半,如何用角度来量化“两周半”?
(2)假如你的时钟快了30 min,现在要校正,需将分针怎样旋转?如果慢了30 min,又该如何校正?
设计意图感受旋转量和旋转方向与之前所学的不同.摩天轮旋转两周半,是旋转了900°,这个度数超出了以前角的范围,角不够用了,说明了扩充角的必要性.时钟快了30 min,需要将分针逆时针旋转180°,慢了30 min,需要顺时针旋转180°,通过旋转分针体现了角的动态定义中的“旋转”,也区别了角的方向.
问题3实际生活中这些角与初中所学的角有所不同,这些角的不同体现在哪几个方面?你能举一些实际生活中的角的例子吗?
设计意图与之前所学的角相比较,一方面,遇到了超过360°的角;另一方面,同样是180°的角,旋转方向不同作用不同.通过归纳,得出角的旋转量和旋转方向与之前所学不同,这就产生了扩充角的必要性.通过举例,进一步感受实际生活中存在超过360°的角,以及不同的旋转方向带来不同含义的角.
1.2 教学设计B
问题1日出日落,寒来暑往……自然界有许多“按一定规律周而复始”的现象,称为周期现象.你们还能举出一些周期现象的例子吗?
设计意图“任意角”是《三角函数》这一章的章首课,三角函数是刻画周期现象的函数模型.让学生通过举例感受自然界存在许多周期现象,如一周七天的变化,一年四季的更替,摩天轮转动时与水平方向的夹角、距离地面的高度等.而已经学习过的函数模型都不能用来刻画这种现象,于是有研究新的函数模型的必要.
问题2刻画周期现象最常见的模型是圆周运动.若点P在以点O为圆心、r为半径的圆周上运动,哪些量是周而复始的?
设计意图研究周期运动,就先研究它的典型代表——圆周运动.带领学生经历数学抽象的过程,将圆周运动抽象为圆O上一点P的运动.在这一过程中,周而复始运动、具有周期性的量有OP与水平方向的夹角、点P的横坐标与纵坐标等.
问题3你能刻画圆周上一点P的位置吗?
设计意图可以用点P的坐标来刻画,这个方法学生最容易想到,建立平面直角坐标系可以准确地表示点P的位置,那么就需要讨论如何建系更合适.这也为后续将角都统一在同一个平面直角坐标系内研究提供了可能.在半径r确定的情况下,点P的位置还可以用射线OP转过的角度或弧长来刻画,这种表示方法也为后续学习“弧度制”作了准备.问题3将《三角函数》这一章要学习的知识有机整合在一起,是对单元教学内容进行整体设计.
问题4如图1,点P1,P2,P3从水平位置A起转过的角分别是多少度?如何区别它们?

图1
设计意图从图形上看,∠AOP1=30°,∠AOP2=30°,∠AOP3=30°,但三个点从水平位置起转动的角度和方向不同,这说明我们需要引入新的概念来区别它们.几何画板动画显示,点P1与点P3相差一圈,出现了超过360°的角;点P1与点P2的运动方向不同,需要引入正角与负角的概念加以区别.这就是扩充角的必要性.
1.3 教学设计C
问题1如图2,摩天轮的半径r为40 m,圆心O距离地面的高度为48 m,摩天轮做逆时针匀速转动,每8 min转一圈.摩天轮上点P的起始位置在最低点处.(1)请用一个量来刻画 1 min后点P的位置.
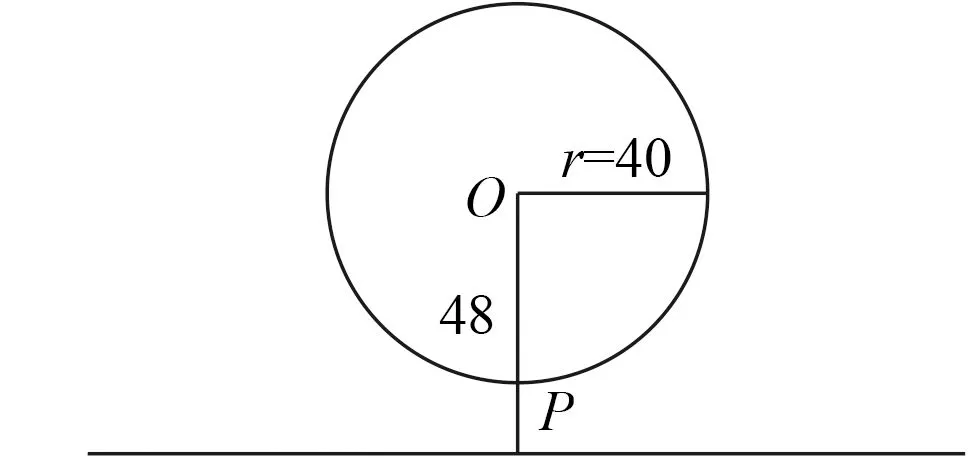
图2
设计意图摩天轮的运动作为例子在这一章的教材中多次出现,贯穿始终.这是一个很典型的周期运动的案例,其中有许多素材与角、三角函数相关联.刻画点P的位置有多种方法,可以培养学生的数学抽象核心素养.点P的位置可以用转过的角度表示;可以用转过的弧长表示;可以用点P距离地面的高度表示;还可以以圆心O为原点、水平方向为x轴建立平面直角坐标系,用点P的坐标刻画.其中,选择角度刻画更直观,点明本节课首先研究角.
(2)1 min后、2 min后、3 min后、4 min后、 8 min后,OP从起始位置所转过的角分别是多少度?
设计意图感受“旋转成角”,并复习初中所学过的锐角、直角、钝角、平角、周角的概念.
(3)9 min后、16 min后,OP从起始位置所转过的角又分别是多少度?
设计意图转过的角分别是405°和720°,遇到了超出0°~360°范围的角,引起了认知冲突,初中所学的角不够用了,需要推广.

图3
问题2摩天轮的半径r为40 m,圆心O距离地面的高度为 48 m,摩天轮做匀速转动,每8 min转一圈.摩天轮上点P的起始位置所对应的半径与地面平行.当摩天轮转动2 min后,求点P离地面的高度.
设计意图由于没有规定旋转方向,转动 2 min后,点P可能运动到最高点,也可能运动到最低点.相同的起始位置、相同的旋转量和不同的旋转方向,得到的角不同.
问题3你能再举一些生活中由于旋转方向不同而角的含义不同的例子吗?
设计意图通过举例,进一步感受角与旋转方向有关.比如拧紧螺帽和拧松螺帽、前滚翻和后滚翻等.
2 三种引入方式的比较分析
2.1 共性
这三种引入环节的教学设计都围绕学生对角的认知冲突展开,充分展现了对角进行推广的必要性;都以问题串的形式呈现,层层递进,每个问题都是学生思维的阶梯;都与生活实际相联系,都通过学生举例的方式将抽象的概念具体化,从而深化对任意角的理解.
2.2 锐角与立意的不同
教学设计A立足于概念产生的必然性,也就是“为什么角的概念要推广”.教师从摩天轮旋转两周半、校准时钟等丰富的生活实例出发,让学生充分感受“角不够用”,再通过比较归纳得出角的概念在旋转量和旋转方向上都需要推广.
知识推广的原则是必要性和可行性.类比数系的扩充,每一次都是数不够用了,于是引入新的数,解决在原有数集中某种运算不能进行的问题.角的概念的扩充,是角不够用了,于是扩大角的范围和规定角的方向,从而解决初中所学的角在现实世界中不够用的问题.
教学设计B立足于大单元教学思想,把一个小节的内容融入整章去通盘考虑.《三角函数》这一章研究的是周期现象,问题1就从这里出发,先请学生举例,感受自然界和生活中的周期现象.问题2将周期运动抽象为圆周上一点的运动,问题3研究圆周上点的位置.在这些问题的研究过程中,虽然没有立即推广角的概念,却在围绕半径、角、弧长、坐标等对象展开,而这些将是本章的重要研究对象,为后续研究作了准备,体现了章首课应有的作用.
数学大单元教学是对知识结构、方法体系和数学思想的整体性教学,是数学教学设计与核心素养的有效对接.一方面,“教前顾后”,为后面的学习开一扇窗、播一粒种,让它在那儿慢慢推开一扇门、萌出一颗芽.另一方面,“学后想前”,引导学生把学习过程中习得的方法迁移到新的问题中,使他们通过主动类比、形成结构并内化为数学学科的核心素养与关键能力.
教学设计C立足于课时整体设计,对核心内容“再建构”,对核心素养“重落实”.整节课用摩天轮的问题将任意角的概念串起来,在引入部分,对摩天轮转过角度的研究使学生感受旋转成角、产生角不够用的冲突,对摩天轮距地面高度的研究使学生直观感受旋转方向对角的影响.在本节课的后续内容中,教师还通过研究摩天轮转到相同位置时转过的角之间的关系来研究终边相同的角的表示方法.本节课行云流水,概念在同一个情境中自然流淌生成.
通过对核心概念的重组和再建构,可以将概念课中比较零散的概念串起来,使概念之间有序、有关联,使整节课有主线.而在有些课堂中,我们看到,学生被教师设计好的一个又一个情境牵着走,虽然也得到了概念,但不能更直接地感受到概念发生发展的过程.对于概念比较零碎的课,比如向量的概念、复数的概念等,都可以采用这个办法.
3 教学启示
3.1 研究章引言,上好起始课
教材的每一章都有章引言,是对本章所涉及的知识和思想方法的介绍,也是这一章的统领.在教学中,这个部分常常被忽视.而教师认真研究章引言,有助于深入理解教材,理解这部分的内容、结构和思想方法,可以说,章引言在教学中发挥着“导游图”的作用.
《三角函数》这章的章引言介绍了周期现象,然而之前所学的函数模型无法刻画周期现象,所以提出问题“用什么样的数学模型来刻画周期运动?”这就使得研究三角函数成为必然,而研究三角函数,首先就要研究角.研究圆周上一点的运动,用不同的量描述同一事物,那么它们之间必然有联系.这就为后续扩充角、引入弧度制、建立三角函数奠定了基础.
“任意角”是《三角函数》一章的起始课,站在整个章节的角度来设计本节课,是建立在课程标准、核心内容、基本学情的深度分析基础上的“再建构”,可以更好地体现推广任意角的作用,教学设计B正是这么建构的.当然,章引言只是引言,涉及到的内容跨度较大,不需要面面俱到,也不宜过分深入,其全部内容随着章节学习的深入而推进展开.
3.2 抓住生长点,引入新概念
在新概念的引入过程中,要关注学生的认知发展水平和已有的知识经验,找准知识生长的起点.本节课的生长点有小学对角的认识、初中学习过的角的概念、实际生活中的需要、数系扩充的体验等,这些都是先行组织者,都为角的扩充奠定了基础.在此基础上发展新概念是自然而然的,也是必然合理的.
教学设计A和教学设计C都抓住任意角的生长点,引导学生亲历新概念的发生发展过程,自然适切.引导学生积极主动地参与学习是落实学科核心素养的关键.如果概念凭空而来,如果仅仅只是规定,学生不可能主动参与学习,核心素养就不可能落地.
3.3 设计好问题,指向有效性
学习发生的基本条件是产生学习需要,教师的一个重要任务就是提出有效的问题,创设学习发生的条件,激发学习需要.我们在听课中,常常听到指向不明确的问题、学生无法回答的问题、细碎随意的问题等.这样的问题不仅不能促进学生思考,反而会阻碍学习的发生.
在这三种引入部分的教学设计中,教师都设计了有效的问题串.问题指向明确,把问题问在学生的最近发展区里,让学生既熟悉又陌生,开始积极思考.问题分层递进,一步一步地揭示知识本质,引导学生由浅入深地思考.问题包含方法,在解决问题的同时也教给学生研究问题的方法路径.

