面向低精度环境的安全高速批图像加密

吴潇飞，岑娟，王振伟，游大涛*，武相军

1.河南大学软件学院,开封 475000; 2.河南大学药学院天然药物与免疫工程重点实验室,开封 475000;3.郑州电力职业技术学院信息工程系,郑州 450000

0 引 言

随着医学、航空航天、军事、云计算和物联网(internet of things, IOT)等领域的发展，通过互联网和无线网络进行数字图像传输的需求也越来越高(Dhall 等，2018)。数字图像具有直观清晰的信息表达能力，承载着大量有价值的信息，因此数字图像信息的安全保护工作至关重要，针对这一需求，研究人员提出了一系列图像加密方法，其中主要有基于小波变换的加密方法(Li等，2018a)，基于DNA编码的加密方法(Zefreh，2020；张晓宇和张健，2021；Ben 等，2018)，基于可逆细胞自动机的加密方法(Souyah和Faraoun，2016)，基于置乱的加密方法(Zhang等，2016；梁颖和张绍武，2018)以及基于混沌系统的加密方法(Chen 等，2020； Liu 等，2021；Xian和Wang，2021；周辉 等，2021；Wang 等，2019)等。

混沌系统因具有初始条件敏感性、不可预测性和便利性等内在特性，使得基于混沌系统的加密方法成为最具代表性和应用最广泛的图像加密方法。然而近期研究表明，大多数现有的图像加密方法的安全性非常值得怀疑(Preishuber 等，2018)，特别是在低计算精度条件下，一些声称具有较高安全性的图像加密方法很容易被攻击者破解(Li等，2018a，b)。为了提升加密方法的安全性，涌现了一些高维加密方法，如改进版2D-SCL(a new 2D hypher chaotic map based on the sine map, the chebysher map and a linear function)加密方法(Chen 等，2020)，这些方法在高精度环境下表现出较高的安全性，然而在研究中发现这些方法的时间复杂度与低维方法相比较高，而且在低精度环境下的安全性也存在严重缺陷。

基于置乱的加密方法(Zhang等，2016)和基于DNA编码的加密方法(Zefreh, 2020)是潜在的可有效运行于低精度环境下的图像加密方法。前者在加密过程中一般直接在像素级或bit位级对图像进行置乱和扩散；后者在加密过程中通常将每个像素分为4组4进制数，之后用DNA的4种碱基分别表示一个4进制数，最后借鉴DNA编码规则对像素内的各组进行置乱和扩散。据此分析可知与混沌加密方法不同，它们主要基于像素的bit位信息进行加密，不需要运行于对精度要求较高的浮点数系统之上，因此它们具有在低精度环境下有效运行的潜力，但是这两类方法在加密过程中通常需要借助混沌系统生成的随机数进行置乱和扩散，这不可避免地严重影响了它们在低精度环境下的安全性。

为了提升加密速度，研究人员提出了几种批量加密方法，主要有压缩加密、多线程加密和组合加密等批量加密方法。压缩加密(Liu 等，2021；Li 等，2021)具有降低传输带宽的优点，但是这类方法不仅会造成图像信息的丢失，而且还依赖于高性能计算设备的支持；多线程加密(Song 等，2020)具有加密速度快的优点，但是对硬件的计算性能要求较高，在计算性能较低的硬件环境下难以正常工作；现有的组合加密方法(Wang 等，2021)虽然是无损加密，但即使在高计算精度环境下其安全性也存在着严重的缺陷，在低计算精度环境下其安全性更低。综上所述，这些组加密方法也难以满足IOT环境下的实际需求。

针对IOT环境下的实际需求及现有加密方法的不足，本文提出了一个基于素数模乘线性同余产生器的批图像加密方法。该加密方法不仅在低精度环境下(如2-8)表现出较高的安全性，而且时间复杂度较低，可以在确保较低时间开销的基础上大幅提升低计算精度下图像加密的安全性。

1 基于素数模乘线性同余产生器的批图像加密方法

混沌加密方法是现有最具代表性的图像加密方法，这类加密方法依赖于浮点数运算，而且对浮点数的精度要求较高，所以在低计算精度环境下这些混沌系统的随机性会遭到严重破坏，导致相应加密方法的安全性急剧降低。研究发现，单字节长度的素数模乘线性同余产生器不仅可以产生取值范围为[0,255]的符合均匀分布的伪随机数序列，而且也可以在加密方法中取代目前广泛使用的混沌系统，使加密方法运行于单字节长度的低精度环境下，摆脱对高精度计算环境的依赖。

在研究中还发现，加密方法的速度虽然受优化方法的影响，但主要取决于加密过程的时间复杂度。现有主流的混沌加密方法大致可分为两类：一类是加密过程中每个像素对应一组混沌随机数，另一类是多个像素对应一组混沌随机数。前者所用的混沌系统每产生一个随机数往往需要数十次的浮点数运算，安全性较高的高维混沌系统所需的计算次数更多；后者虽然需要产生的随机数数量相比前者大幅降低，但是在加密过程往往需要多轮加密，因此它们的时间开销均较大。本文方法提升加密速度的核心思路是在尽可能降低产生一个随机数所需计算次数的同时，使多个像素对应一个随机数且仅需单轮加密。该思路可以从理论上保证本文方法具有相对较低的时间复杂度。

基于上述思路，提出了一个基于素数模乘线性同余产生器的批图像加密方法。

1.1 素数模乘线性同余产生器

在研究中发现，基于单字节长度的素数模乘线性同余产生器可以在低精度环境(如2-8)下产生符合均匀分布的取值范围为[0,255]的伪随机数列，该数列可以取代混沌系统用于低精度环境下的图像加密。根据上述发现，本文在 Wichmann和Hill(1982) 的基础上提出了一个单字节环境下素数模乘线性同余产生器(prime modulo multiplication linear congruence generator，PMMLCG)，具体计算为

(1)

为了分析PMMLCG的随机性能，展示了PMMLCG生成的伪随机序列的直方图和散点图。图1和图2分别是使用式(1)生成伪随机数的归一化直方图和依据生成时间序列显示的前13 000个伪随机数的散点图。从图1和图2可以看出，由素数模乘线性同余产生器产生的伪随机数列符合均匀分布，因此可以在加密方法中使用该产生器代替经典的混沌系统。

1.2 基于PMMLCG的批图像加密方法

该加密方法可以分解为7个步骤，分别是图像集哈希值的生成、组合图像的生成、组合图像的更新、加密序列矩阵的生成、图像置乱、置乱图像的加密和加密序列矩阵的加密(如图3)，具体内容如下：

1)生成图像集的哈希值。为了增强加密方法的敏感性，采用SHA-1(secure hash algorithm-1)方法生成图片集的哈希值。具体方法是将尺寸为M×N的K幅图像作为SHA-1的输入，其输出可转化为20个单字节的数字H(s),s=1,2,…,20，每个数字H(s)的取值范围是[0,255]。

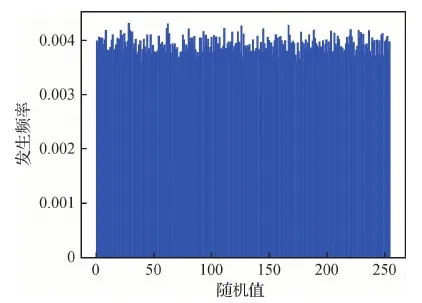
图1 PMMLCG生成的伪随机数序列的直方图Fig.1 Histogram of generated pseudo random numbers by PMMLCG

图2 PMMLCG生成的伪随机数序列的散点图Fig.2 Scatter plot of generated pseudo random numbers by PMMLCG

图3 加密方法流程图Fig.3 The flow chart of encryption method

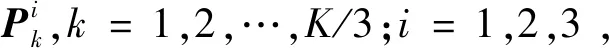
(2)

之后，依次对第1组内所有图像中位置为(1,2),(1,3),…,(2,1),(2,2),(2,3),…,(M,N)的像素值分别进行上述异或操作(⊕)，直至生成一幅尺寸为M×N的新图像p1；最后，分别在第2组和第3组内进行上述操作，生成p2和p3。

3)更新p3。为了提高加密方法的敏感性，借助哈希值H(s)对p3进行更新。具体更新为

p3(m,n)=p3(m,n)⊕H(s)

(3)

式中，p3(m,n)表示组合图像p3中坐标为(m,n)的像素值，N表示图像中每行的像素数量，s表示哈希值的编号，计算为

s=[(m-1)×N+n] mod 20

(4)

4)加密序列矩阵的生成。为了对图像集内的所有图像进行加密，这里基于PMMLCG和上述组合图像生成一个伪随机数列矩阵。生成方法为

(5)

式(5)是式(1)的具体应用。式中，p1(m,n)、p2(m,n)和p3(m,n)分别表示p1、p2和p3内坐标为(m,n)的像素值，q1、q2和q3代表经过异或后的像素值，Q(m,n)表示根据q1、q2和q3计算得到的图像Q内坐标为(m,n)的伪随机数。该步骤生成的Q作为加密序列矩阵用于后续步骤中的图像置乱和扩散。

(6)

1.3 解密方法

解密部分主要由加密序列矩阵解密、密文解密和逆置乱3部分组成：

(7)

2 实验仿真分析

仿真实验中计算机的配置为Intel(R) Core (TM) i7-10710 CPU @ 1.10 GHz，内存是16 GB，操作系统是Windows10；仿真软件采用Pycharm2019.2.4×64。本文使用基于DNA的加密方法(Zefreh, 2020)、比特置乱加密方法(Zhang等，2016)和混沌加密方法(Chen 等，2020; Liu 等，2021)作为实验对比对象，此4种方法可以分别代表现有的经典图像加密方法。实验图像来自于USC-SIPI-Miscellaneous数据集，从中随机选出100幅512×512 像素的图像作为测试数据。为了便于展示加密效果，选择4幅具有代表性的图像进行展示(见图4)。

2.1 相关性分析

相邻像素相关性通常用于评价图像加密方法的性能。两个相邻像素序列的相关性可以计算为

(8)

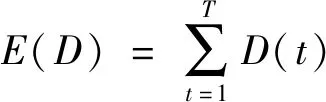
2.2 信息熵

信息熵是评价图像加密方法随机性的一种常用方法。图像c的信息熵使用I(c)表示,具体计算为

(9)

式中，i表示范围从0到255的图像像素值，Pc(i)是图像c像素值为i的概率。对于每个通道的彩色图像或灰度图像，它们最大信息熵的值为8。表2列出了不同图像及其在不同方法下对应的加密图像的信息熵。该表显示所有加密方法生成的密文的信息熵都极其接近8。

2.3 像素敏感性

为了测试本文加密方法的敏感性，采用通用的明文敏感性检测方法对本文加密方法进行测试，并计算相应图像的近邻相关性用于量化展示本文方法的像素敏感性。具体测试方法为(图6)：首先改变明文图像集100幅图像中一幅图像的一个像素值，如图6(a)(b)，将图6(a)减去图6(b)可得图6(c)，之后计算图6(c)的近邻相关性，在水平、垂直和对角线上均约为1，从图6(c)及相关系数可知图6(a)与图6(b)间高度相关，它们区别很小。接着将图6(a)和图6(b)按照本文方法进行加密，分别得到图6(d)与图6(e)，之后将图6(d)减去图6(e)得到图6(f)，最后计算图6(f)的近邻相关性，在水平、垂直和对角线上分别为-0.022 5、0.002 8和-0.007 3，从图6(f)及相关系数可知，图6(d)和图6(e)间不相关，它们区别极大。从上述分析可知，本文加密方法的像素敏感性较高，对任一像素的微弱变化极为敏感。

在密钥方面，本文加密方法与现有混沌加密方法存在较大差异。前者在加密图像时直接使用以组合图像为初始值产生的伪随机数列矩阵，之后使用任何合适的现有加密方法对该矩阵加密，因此本文加密方法加密后的组合图像并不作为密钥使用，可以直接丢弃；而后者在加密图像时使用基于初始值产生的伪随机序列，加密后还需保存初始值作为后续解密的密钥。因此现有密钥敏感度测试方法并不适用于评估本文加密方法的密钥敏感度，所以不对密钥敏感度进行评估和展示。

图4 4幅图像的加密解密效果图Fig.4 Encryption and decryption results of four images((a) four images；(b) histogram of images；(c) encrypted images；(d) histogram of encrypted images；(e) decrypted images)

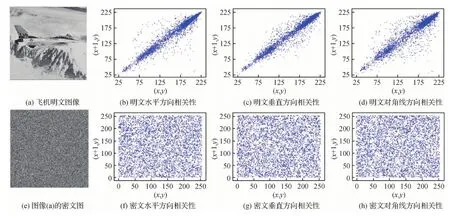
图5 飞机图像相邻像素的相关性Fig.5 The adjacent correlation of airplane((a) airplane image；(b) horizontal direction of (a)；(c) vertical direction of (a)；(d) diagonal direction of (a)；(e) encrypted image of (a)；(f) horizontal direction of (e)；(g) vertical direction of (e)；(h) diagonal direction of (e))

表1 相邻像素的相关系数Table 1 The correlation coefficient of adjacent pixels

表2 不同图像信息熵Table 2 The information entropy of different images

图6 像素敏感性Fig.6 Pixel sensitivity((a) airplane image；(b) airplane image changed one pixel；(c) subtraction of (a) and (b)；(d) encrypted (a)；(e) encrypted (b)；(f) subtraction of (d) and (e))

2.4 密钥空间

众所周知，为了确保加密安全性，加密方法的密钥空间应不小于2128。本文和对比方法在不同计算精度下的密钥空间记录于表3中。从表3可知，在计算精度为2-16和2-8环境下，本文的密钥空间均为2(8×512×512)，远大于2128，足以满足密钥安全性的要求；而改进版2D-SCL加密方法虽然在计算精度为2-16环境下的密钥空间是0.3×2158，可以满足密钥安全性的需求，但是在计算精度为2-8环境下的密钥空间是0.3×294，远小于2128，不满足密钥安全性的要求。基于DNA、混沌和哈希值混合模型加密方法的密钥空间在计算精度为2-16和2-8情况下的密钥空间都小于2128，低于安全性要求；基于耦合分段正弦映射和敏感扩散结构的混沌图像加密算法在计算精度为2-16和2-8情况下的密钥空间都远小于2128，不能满足安全性要求；采用比特置乱的加密方法的密钥空间虽然在计算精度为2-16环境下是0.4× 2128+2131，可以满足密钥安全性的需求；但是在计算精度为2-8环境下的密钥空间为0.4×264+267，不能满足密钥安全性要求。

表3 不同算法密钥空间对比Table 3 The key space of different encryption algorithms

2.5 抗差分攻击分析

差分攻击是一种常用且高效的安全攻击方法。像素数量变化率(number of pixel changing rate, NPCR)和统一平均变化强度(umified average changed intensity, UACI)是评价抵抗差分攻击能力的两个常用指标。NPCR用于统计不同像素的数量，而UACI用于统计两幅图像之间像素的平均变化。假设d1和d2是两幅密文图像，它们对应的明文图像只有一个比特值的差异，则NPCR和UACI计算为

(10)

式中，δ是一个符号函数，如果d1(t)等于d2(t)，那么δ(d1(t),d2(t))=0。否则，δ(d1(t),d2(t))=1。此外，T表示密文图像的总像素数量，F表示最大允许像素值，通常设置为255。理想情况下NPCR的值为μN=0.996 1，UACI的值为μU=0.334 6，根据Chen 等人(2020),在α水平上，通过式(11)和式(12)判断当前NPCR是否处于标准范围内。

(11)

(12)

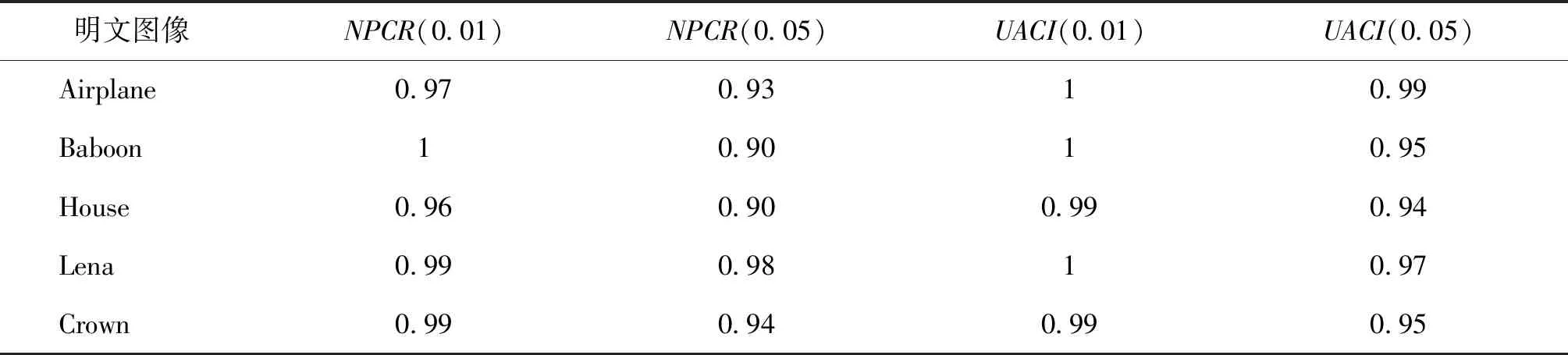
当NPCR

与NPCR类似，UACI也有相应的标准，在α水平上，由式(13)和(14)判断当前UACI是否处于标准范围内。

(13)

(14)

借鉴Chen 等人(2020)的参数设置,这里将显著性水平α设置为0.01和0.05。通过计算可得，N*(0.01)=99.581 0,N*(0.05)=99.589 3,

实验将每幅图像测试100次，每次在某幅图像随机选取一个像素并改变其中1个bit位的值，然后使用本文方法对数据集进行加密。根据上述公式计算得到的结果展示在表4中。表4显示，本文加密方法的通过率可以稳定达到90%以上，根据Wu 等人(2011)可知，本文方法能够有效抵抗差分攻击。

表4 不同显著性水平下NPCR、UACI通过率Table 4 The pass rate of NPCR and UACI with different levels of significance

2.6 抗明文攻击

已知明文攻击和选择明文攻击是破解加密图像的常用方法。一个安全的加密方法应该具备较强的抗明文攻击能力。纯白和纯黑色图像会使加密方法的置乱效果失效。黑客经常使用这种类型的图像来破解加密方法。因此，它们常用于评估加密方法对已知明文和选择明文攻击的抵抗力，图7展示了纯白和纯黑色图像加密的效果，可以看出加密图像都是类噪声图像，并且直方图是均匀分布的，这意味着不能从这些加密图像中获得任何关于普通图像的信息。表5展示了纯白和纯黑色图像密文的相关性、信息熵以及NPCR与UACI值。数据显示密文的近邻像素的相关性、信息熵、NPCR和UACI均接近于理想值，进一步证实了本文方法具有较强的抗明文攻击能力。

2.7 抗遮挡和抗噪声攻击

在加密图像传输过程中，不可避免会存在数据丢失或变异的问题，使加密图像必然面临遮挡和噪声的干扰，因此抗遮挡和抗噪音攻击也是图像加密方法需要具备的必要能力，对进一步提升加密方法的安全性具有重要意义。这就意味着对于一个理想的加密方法来说，它必须对普通图像的微小变化甚至一个像素的变化极其敏感，而加密图像的像素变化对解密过程的影响较小。具体评估方法如图8所示。抗遮挡攻击的评估方法如下：将加密图像(图8(b))遭受遮挡攻击后得到遮挡图像(图8(c))，之后对遮挡图像(图8(c))再用普通的方式进行解密，得到图像(图8(d))。抗噪音攻击的评估方法如下：将原图(图8(a))加密得到密文图像(图8(b))，在密文图像(图8(b))中加入散斑噪音得到遭受噪音攻击后噪音图像(图8(e))，之后对图像(图8(e))进行解密，得到噪音攻击后的解密图像(图8(f))。由解密后的图像(图8(d)和图8(f))可知，该方法对遮挡攻击和噪音攻击具有一定的鲁棒性。

图7 纯白和纯黑色图像加密结果Fig.7 Encryption results of all-black and all-white images((a) all-white image；(b) encrypted image of (a)；(c) histogram of (b)；(d) all-black image；(e) encrypted image of (d)；(f) histogram of (e))

表5 纯白色与纯黑色性能评估指标Table 5 The performance assessment results of all-black and all-white images

2.8 时间开销对比

除了加密方法的安全性以外，运行速度也是评价图像加密系统性能的一个重要指标。由于本文方法在加密过程中使用多像素对应同一个伪随机数，因此有效降低了加密的时间开销，提升了加密速度。表6展示了对50～800幅普通图像进行加密所需的时间开销，可以看出在多图像加密时，本文方法所需的加密时间开销不仅低于目前具有较低时间开销的混沌加密方法(Chen等，2020)，而且也远低于基于DNA和位置乱的代表性加密方法所需的时间开销，证实了本文方法具有较高的加密速度和效率，达到了预期目标。

3 结 论

本文针对在低计算精度环境下现有图像加密方法的安全性和速度均较低的问题，基于素数模乘线性同余产生器提出了一种具有较高安全性和加密速度的批图像加密方法。通过使用基于单字节的素数模乘线性同余产生器代替混沌系统，确保该加密方法可以安全有效地运行于低精度计算环境下。在加密过程中使用多像素对应同一个伪随机数，有效降低了加密的时间开销，提升了加密速度。此外，借助哈希值提升了加密方法的敏感性。实验结果表明，该方法显著提升了低计算精度环境下图像加密的速度和安全性。然而组合图像的生成及加密序列矩阵的生成等方面的时间开销依然较大，在确保安全性的基础上，如何进一步降低上述过程的时间开销是后续研究需要关注的问题。

图8 抗遮挡攻击与抗噪声攻击Fig.8 Anti-occlusion attack and anti-noise attack((a) airplane image；(b) encrypted image；(c) encrypted image with 0.2 data loss；(d) decrypted image with 0.2 data loss；(e) encrypted image with 0.05 speckle noise；(f) decrypted image with 0.05 speckle noise)

表6 不同方法时间开销对比分析Table 6 The test result of time consumption of different schemes /s