从一道高考题变式谈指对混合式的五种处理思路
李志娜
(河北省邯郸市第一中学 056002)
邯郸市2022届高三质检考试的压轴导数题,是一道指对混合的不等式恒成立问题.题目如下:
已知函数f(x)=aex-1-x.
(1)讨论函数f(x)的单调性;
(2)若f(x)+x-1≥lnx-lna恒成立,求实数a的取值范围.
可以看出,此题第(2)题与2020年山东高考试卷的第21题基本相同.此题可从不同角度解决,有多种思路和方法,略去第(1)问,现将第(2)问的5种思路整理分析如下.
1 含参分类讨论


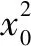
3.2 齐次化构造函数
点评这类构造将多元变量利用齐次式变成单一变量,再构造函数进行解决,可以减少多变量带来的麻烦.
目前,纸病在线检测系统普遍采用“电荷耦合器件(Charge Coupled Device,CCD)相机+计算机”的硬件结构模式,通过CCD高速相机实时采集纸张图像数据并传送至检测系统PC端,系统的核心处理器利用图像处理技术对纸张图像进行处理和辨识,实现对黑斑、孔洞、划痕、裂边等缺陷的识别和分类[1- 3]。但是随着纸机车速的提升、纸幅的加宽以及对纸病辨识精度的提高,CCD相机采集到的海量图像数据,给系统的快速性甚至稳定性带来了巨大冲击,如何解决打破纸病辨识快速性这一瓶颈已成为当前研究纸病检测技术的关键问题。
4 结语
新高考背景下函数的运用依然广泛,对于构造函数,需要打破原题中的思维束缚,灵活地运用构造法,找准最能反映考题结构特点的函数,以便使问题得到快速的解决.这就要求学生在平时的学习中要善于积累,大胆尝试,将“构造”摆心间,这样面对复杂的压轴题时才能做到“不畏浮云遮望眼”.

当a=1时,g(x)≥g(1)=0,故a=1符合题意.
当0 综上所述,a的取值范围是[1,+∞). 方法2(必要性探路+换主元) 令g(1)=a- 1+lna≥0,得a≥1.令t(a)=aex-1+ lna-lnx-1,因为ex-1>0,所以t(a)为[1,+∞)上的增函数,故只须证明a=1时,g(x)=ex-1-lnx-1≥0.因为ex-1≥x,lnx≤x-1,所以g(x)≥0. 上述思路是处理不等式恒成立问题的常见思路,但由于指对数同时出现,使得构造的含参函数最值经常会出现隐零点的问题,计算量和思维量都较大. 方法3(和型同构1) 由于aex-1-1≥ lnx-lna恒成立,即eln aex-1≥lnx-lna+1,所以ex+ln a-1+x+lna-1≥eln x+lnx.因为y=et+t为增函数,所以x+lna-1≥lnx恒成立. 或ex+ln a-1+ln ex+ln a-1≥x+lnx,利用y= lnt+t的单调性,转化为ex+ln a-1≥x恒成立,即x+lna-1-lnx≥0,由常见不等式x-1≥ lnx易得a的范围. 图1 上述思路需要学生能够从指对数同时出现的式子中,观察并构造出同构,即同为和型或积型.这种思路对学生处理代数式的变形能力要求比较高. 方法8(放缩法1) 因为x>0,a>0,所以 ex≥x+1,ex-1≥x,故aex-1≥ax(当x=1时取等号).又因为lnx≤x-1(当x=1时取等号),所以aex-1-lnx+lna-1≥ax-x+1+lna-1=(a-1)x+lna. ①a=1时,ex-1-lnx-1≥x-x+1+ ln 1-1=0,此时不等式恒成立; ②a>1时,aex-1-lnx+lna-1≥(a-1)x+lna,因为x>0,a>1,所以(a-1)x+ lna>0,即不等式恒成立; ③0 所以,a≥1. 方法9(放缩法2) 将aex-1-lnx+lna-1≥0变为ex+ln a-1-lnx+lna-1≥0.因为ex+ln a-1≥x+lna(当x+lna=1时取等号),lnx-lna+1≤x-lna(当x=1时取等号),所以ex+ln a-1-lnx+ lna-1≥x+lna-(x-lna)=2lna.令2lna≥0,得a≥1.以下同方法8的③. 采用指数和对数式同时放缩是非常大胆的尝试,也有可能放缩过度.可以鼓励学生只对指数或对数放缩.另外,放缩后参数范围是否保持不变,如aex-1-lnx+lna-1≥0恒成立与ax-lnx+ lna-1≥0恒成立,理论上是否等价?不等价又如何处理?可进一步思考. ②当0 所以,a≥1. ①令lna≥-lna,则由f(x)min≥g(x)max,故a≥1(此范围可能偏小); ②当0 所以,a≥1. 本题为指、对混合的不等式恒成立问题,解题思路非常广泛,用所有处理指对混合式的方法基本都可以解决,可见此题非常经典,擅长各种方法的学生都可以上手一试.2 同构法




3 反函数法
4 放缩法
5 凹凸转换法



6 结语

