面向资源均匀使用需求的工业5G实时调度方法
田 宇,陈文谣,关锁玲,许 驰,夏长清,金 曦
1(中国科学院 网络化控制系统重点实验室,沈阳 110016)2(中国科学院 沈阳自动化研究所,沈阳 110016)3(中国科学院 机器人与智能制造创新研究院,沈阳 110169)4(中国科学院大学,北京 100049)5(沈阳工业大学,沈阳 110870)
1 引 言
随着无线技术应用的日益普及,在一些特定工业场景中无线通讯技术正逐渐取代有线通讯技术[1-3].目前,在诸多的无线网络中,最接近工业运动控制系统需求的是5G无线传输技术,5G所支持的高可靠性超低时延在一定程度上满足了运动控制系统以及工业实时系统对无线网络的基本需求.本文关注非授权频段的私有5G技术,该技术无需运营商支持,具有灵活性高、可控性高、隐私安全保障性强等特点.但由于非授权5G使用带宽有限的ISM(Industrial,Scientific,Medical)频段,在这种情况下,数据传输所用资源的分配会对关键数据传输的实时性造成较大影响,而关键数据的实时到达对保证工业实时控制系统的稳定运行具有重要意义.如果数据延迟到达,不仅影响实时控制系统的稳定运行,还可能导致控制系统的瘫痪,甚至严重危害人员生命安全.因此为确保关键数据传输的实时性,需在低时延5G无线传输技术的基础上为其分配确定性的传输资源.
比如在实时控制的移动机器人系统中,如图1所示.控制器通过与5G基站相连下发控制命令,携带移动终端的机器人通过5G移动终端接收控制命令并执行,进而产生反馈信号通过同一无线链路返回到控制器.
在这样的一个面向运动需求的实时控制系统中,既存在固定周期的周期性数据,也存在特定事件触发的突发数据.对于固定周期的时间触发数据,可以进行预先的资源分配,平衡各控制回路之间的资源占用,同时保证各控制回路之间资源占用不冲突,并满足其截止时间限制.而对于事件触发的环境,动作是按需执行的,即由某个事件触发.事件发生的时刻无法预知,因此无法预先为其分配资源.现有工业无线网络的实时调度研究中,大部分只关注时间触发数据的实时调度,仅有少量研究考虑了事件触发数据的传输需求,但都为事件触发数据添加了行为限制条件,例如限制了最短的事件触发数据生成间隔,限制了事件触发数据的并发性等.这些限制使理论模型不同于真实系统,相关研究也无法实际应用.事件触发数据的生成时间完全随机,为使任意时刻生成的事件触发数据都能够得到所需的传输资源,分配给时间触发数据资源后,剩余的空闲资源应均匀分布在时间维度上.因此本文提出一种时间触发数据的调度算法,该算法不仅能确保时间触发数据的实时性和可靠性,还能够为事件触发数据均匀的预留空闲资源.从而为不可预知的事件触发数据的资源分配做出最快速的响应.
2 相关研究
工业无线网络的实时调度已被广泛研究,在文献[4,5]中该问题是NP难问题的推论被首次证明,同时该研究给出了网络可调度的必要条件.此后,为了提高工业无线网络的实时性能,研究人员提出了许多针对周期性时间触发数据的实时调度算法,例如5G中可变参数集与资源位置的协同优化[6,7],根据节点数据流进行分段时隙的分配[8],通过算法分离对工业无线网络的实时性和可靠性进行优化[9],以及资源空间复用[10]等.这些方法在考虑将时隙资源分配给时间触发数据的同时,追求的是工业无线网络在可靠性和实时性方面的提升.如果考虑事件触发的数据包的加入,则会对时间触发的数据包的时隙资源分配结果产生影响,从而导致资源利用率降低.甚至对系统可靠性产生影响.
为了处理事件触发的数据包,一些方法允许事件触发数据包占用时间触发数据包的资源[11],或者分配两种数据包可共享的时隙资源[12],并在事件触发的数据包到来的时候,暂停时间触发的数据包的传输[13].但是在这些方法中,事件触发的数据包的引入可能会引起时间触发数据包的延迟到达甚至丢失.另外,在文献[14,15]中的工作通过抢占式方法对事件触发数据包进行调度,但该方法同样可能会影响时间触发数据包的分配方案,甚至通过抢占造成数据包的丢失.本文提出一种为时间触发数据包均匀分配资源的方法,在不允许事件触发的数据包抢占时间触发的数据包的前提下,以及在不暂停时间触发的数据包传输的同时,在最短时间内保证对事件触发数据包的资源响应.
3 系统模型及问题描述
本文针对时隙分配进行理论及算法上的研究,解决尽可能将时间触发数据占用资源在时间维度均匀分布的问题.
如图1所示,在大多数面向运动控制需求的实时控制系统中[16],均可以有如下控制过程描述,其中,Ci(i∈[1,n],n∈Z+)代表控制器节点,多个控制器与5G基站相连.Oi(i∈[1,n],n∈Z+)代表被控对象节点,与5G终端相连.此类系统中,控制拓扑如图2所示,控制器Ci发送控制命令ci,依次经由5G基站和终端达到执行器,此过程称为下行传输.被控过程包括执行器、设备以及传感器[17],Oi执行控制命令后,传感器产生反馈信号fi,经由5G终端和基站返回控制器Ci,此过程称为上行传输.其中{fi,ci|i∈[1,n],n∈Z+}的传输和被控过程构成一条闭环反馈控制回路,各控制回路在控制层面相互独立.

图2 控制系统拓扑图
每个控制回路中的数据传输可视为一个任务流.一个任务流每隔一个周期时间发起一个控制命令数据包,该数据包必须在该周期内完成回路内的上下行传输,即该回路视为任务流的路径,周期视为传输的相对截止期.
本文采用N={n1,n2,…}表示任务流集合.任务流ni对应一个二元组属性

图3 处理时间在周期中的位置
本文中周期采用调和周期(harmonic period),可以表示为每个周期性任务流的周期Ti=s′×2n,n为非负整数,s′为单位周期中时隙的数目.由于调和周期可以通过改变n的数值刻画差异性较大的多种周期,因此在工业网络中被广泛使用.由于本文对周期性时间触发数据进行实时调度,故将不同任务流周期的最小公倍周期定义为超周期(既最大调和周期),并针对一个超周期内的时隙资源进行调度.由于每个超周期内调度需求与调度结果完全相同.因此本问题只关注一个超周期内被占用资源的分布情况.
在网络层面,任务流数据之间的资源占用冲突,任务流本身的命令先后顺序依赖.基于该问题,本文针对单一信道进行时隙资源调度,即对于单一任务流而言,由于实时控制系统传输的控制命令大多为不超过20字节的短包,故可认为一个时隙资源就可以满足一个控制命令所需资源,对于反馈信号也基于此设定.如图3所示,控制信号ci占用一个时隙资源,反馈信号fi占用一个时隙资源,两个信号之间要满足处理时间不小于ti限制.并且假设在时隙0时,所有时间触发的数据流释放第一个数据包.
当将本文的问题模型考虑为一个可满足性问题时,并将该问题的ti变为0,则该问题规约成与文献[5]中的问题相同,文献[5]中的问题是NP-hard问题,因此本文仅约束部分就NP-hard问题,加上该模型的目标后,本文的问题至少是NP-hard问题.
4 调度方法
各任务流之间存在复杂的依赖和冲突关系,数据包由控制器节点C{C1,C2…Cn}经过5G无线链路到达被控对象节点O{O1,O2…On},在单一信道中,由于存在调度冲突,使得传输无法并行,基于这些限制,本文进行了如下规划.
设xi,j表示任务流i是否占用时隙j,xi,j∈{0,1}.
·xi,j=1 表示任务流i占用时隙j;
·xi,j=0 表示不占用.
其中i表示任务流的序号,j是超周期中数据时隙的编号,设路径上的任务流个数为n,超周期中时隙总数为m,则有1≤i≤n,1≤j≤m.此时最小任务流周期占用时隙的最大值可以表示为:
(1)
其中p表示任务流周期集合Ti中的最小周期,即p=minTi,Smax表示时隙占用数目最多的最小周期p内所占用的时隙数目.本文时隙分配的目标就是均衡每个最小周期内的资源占用,因此目标为最小化Smax的值,即:
(2)
问题规划满足以下约束:
1)唯一性约束.多个任务流不可占用同一时隙j,因此:
(3)
2)实时性约束.每次回路控制从控制命令生成到收到反馈必须在一个周期内完成,即任务流i在每个Ti内需占用2个时隙,因此:
(4)
3)处理时间约束.任务流i在该任务流周期Ti内所传输的两个数据包在时间上满足时间差不小于处理时间ti,因此:
(5)
根据公式(1)-公式(5),本文使用ILOG CPLEX对该规划进行求解,ILOG CPLEX是IBM推出的一款优化模型工具箱,并提供特定的编程语言.对于0-1整数规划问题,在存储空间和时间允许的情况下,ILOG CPLEX一定能找到最优解.对于本文的问题,公式(1)-公式(5)可以表示为0-1整数规划问题,其中xi,j为变量,通过ILOG CPLEX自身语言将公式(1)作为CPLEX的目标函数,公式(2)-公式(5)作为规划的约束条件,再利用CPLEX调用自身优化算法进行最优解的求取.
5 改进问题模型
对于本文中的问题模型,在时间和存储允许的情况下,规划求解器可以求得该问题的最优解,但随着问题规模的增大,求解时间也随之急剧增加,因此本文进一步提出了改进算法,以缩短求解器求解时间.
由于本文中问题目标是使占用的时隙资源尽量均匀的分配在时间维度上.具体来说是使每个最小任务流周期p内占用时隙数目最多的周期占用时隙数目最少.基于这样的一个目标,从最优解的方向考虑,本文进一步提出了最小任务流周期p内占用时隙总数的限制S.即:
(6)
在式(6)的限制条件下,解空间大小受S约束,通过由小至大调整S的取值,可指导求解器的寻优过程,改进算法如算法1所示.
算法1.相对最优限制算法
输入:S,set_t,s_add=1
输出:调度结果,求解时间
2.whileS 3.Solver(S,set_t)//定义求解函数Solver() 4. 记录时间; 5.if!solvethen//无解 6.S←S+s_add; 7.else 8.returnSolver调度结果和求解时间; 9.endwhile 10.return调度失败; 本文提出的相对最优限制算法(算法1)是通过公式(6)对第4节模型进行简化,在公式(6)极大缩短求解时间的前提下,能够快速找到可行解. 虽然用CPLEX求解器可求得该问题的最优解,但随着问题规模的增大,求解时间随之增大,即使在改进问题模型下,求解时间依然急剧增加.因此本文又提出启发式算法用以提高问题规模的可扩展性. 规则1. 对最小周期任务流即周期为T0的任务流进行调度,为使占用资源尽量平均(设该任务流开始周期为第0个周期),当i为偶数时,将第i个周期内的后一个数据包放到第i个周期末尾处,即X(i+1)T0-1=1,在该周期内时隙间隔为T0/2处(通过改变时隙间隔来确定ti),放置第2个数据包,即X(i+1)T0-1-T0/2=1.当i为奇数时,将第i周期内的第1个数据包放到第i个周期开始处,在该周期内时隙间隔为T0/2处,放置第2个数据包.如果最小周期的任务流不唯一,则在偶数周期内按该方式向前移动一个时隙,在奇数周期内向后移动一个时隙,依此规则,放置周期均为最小周期的任务流.如果时隙占用冲突,则无解. 对于非最小周期任务流中最小周期的任务流,分为以下两种规则. 规则2. 如果该任务流周期为T0的2倍,则将该周期内的两个数据包分别放在周期首尾处.若有相同周期的任务流,则分别从首尾处向前移动一个时隙,放置数据包,如果占用冲突,则无解.根据规则1的推导,该任务流一个周期内的两个数据包之间的距离满足ti限制. 规则3. 若周期不是T0的2倍,则从前到后查找该任务流每个周期内的第1/4周期和第3/4周期中的空时隙,若有空时隙,则在第0-1/4周期的第1个空时隙放置第1个数据包,在第2/4-3/4周期的第1个空时隙放置第2个数据包.若其中一个1/4周期内无可占用时隙,则无解.对于拥有同样周期的任务流,则在1/4-2/4周期内和3/4-1周期内分别放置一个数据包,而后据此规则循环,若其中一个1/4周期内无可占用时隙,则无解. 规则4. 对于剩余任务流,执行规则3. 算法2.启发式算法 输入:时隙总数m,任务流总数n 输出:调度序列X 1. 随机生成n个任务流数组T 2.T←sort(T)//定义排序函数sort() 3. 计算相同周期的个数,并存入数组K 4.Xi={0} 5. 数组arrd记录空时隙位置 6.fork∈[0,K0)do 7.fori∈[0,m/T0)do 8. 执行规则1 9. 更新X,addr 10.endfor 11.endfor 12.if(K1==0)return求解结果 13.endif 14.elseif(K1!=0&&TK0==2*T0)then 15.fork∈[0,K1),i∈[0,m/TK0)do 16. 执行规则2 17. 更新X,addr 18.endfor 19.endelseif 20.else 21.fori∈[1,n)do 22. 执行规则3,4 23. 更新X,addr 24.endfor 25.endelse 26.return求解结果 算法2在初始化随机任务流数组T后,对T进行排序(第2行),并计算相同周期的个数,存入K(第3行),同时初始化调度序列X={0}(第4行),记录空时隙位置(第5行),然后根据规则1对最小周期任务流进行分配(第6-13行),根据规则2对非最小周期进行分配(第14-18行),最后根据规则3、规则4对剩余任务流进行分配(第19-25行). 本实验通过对比CPLEX方法(公式(1)-公式(5))、改进模型算法(算法1)、均分算法和启发式算法(算法2)的执行效果与执行时间,说明各算法特性.其中均分算法是指上行资源与下行资源只允许分别使用整个任务周期的一半.该方法通过一种直观的方式限制了变量的取值范围,达到了缩短求解器求解时间的目的. 图4描述了CPLEX方法,改进模型算法,均分方法对2000个任务流调度执行时间的分布.该组对比中a=0.2,n=4,在这种情况下,极少数任务流的求解时间大于10秒,说明在10秒的时间范围内,得到了绝大多数的最优解.同时,在执行时间长短分布状态上,均分方法优于改进模型算法,改进模型算法优于CPLEX方法. 图4 不同方法执行时间分布 图5(a)表示不同方法执行时间的对比.在任务流数目为4-7的情况下,改进模型算法的执行时间逐渐接近CPLEX求解器的执行时间,说明随着任务流数目的增多,改进模型算法的在执行时间上的优势逐渐减小.而均分方法在执行时间上优势明显,原因是限制变量的取值范围来换取执行时间的减少.随着节点数目的增加,在n=8时,CPLEX方法与改进模型算法在不限制执行时间的情况下,两小时未得到最优解. 图5(b)对比了改进模型算法,均分方法和启发式方法的调度成功率,在n=12时,启发式算法的调度成功率开始下降,随着n的增大,3种方法的调度成功率均有所下降,原因是调度复杂度增加,时隙占用冲突增加.而在调度成功率方面,改进模型算法由于限制较少,可调度行更加灵活,成功率更高.启发式算法相比于均分方法,灵活性较低,调度成功率相对较低. 图5 执行时间与调度成功率对比 图6对比了改进模型算法(算法1),均分方法和启发式算法所调度结果的优劣程度,在不同任务流数目的情况下,改进问题模型算法和均分方法所调度的结果的方差波动范围小,说明这两种方法的调度结果接近理论值.原因是这两种方法均能在时间和存储空间允许的范围内找到非劣解.但相比来说,改进模型算法优于均分方法,原因是改进模型算法对变量的限制条件相对少,可求解范围大,非劣解可选择数目多. 图6 结果方差对比 启发式算法在n=4时,调度结果较好,但随着n的增加,启发式算法的调度结果与理论值之间的方差增大,原因是启发式算法在均匀分配调度空间的时候,并未考虑时隙占用数目最少的周期p这一因素.但该方差反映在时隙数目和理论值的差距上时,结果可以接受. 为使事件触发数据能够尽快得到5G网络的响应,本文将时间触发数据占用的资源均匀的分布在时间维度上,提出了时隙资源均匀占用的调度模型,并将该模型描述为求解器可解的0-1整数线性规划问题.之后,为缩短求解器的执行时间,对该模型进行改进,通过变量控制解空间大小,实现了在较小解空间内的快速求解.但随着问题规模的增大,本文又提出一种启发式算法来增加问题可扩展性.最后通过实验可以得出,改进模型算法,均分方法,启发式算法各有优劣,可根据不同需求选择相应的调度方法.6 启发式调度
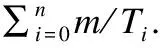
7 实 验




8 结 论

