主跨150m自锚式悬索桥体系转换施工监控实践研究
梁家熙 彭世杰 刘 阳
(珠海交通集团有限公司,广东 珠海 519000)
自锚式悬索桥多采用“先梁后缆,再张拉吊索”的施工工序,通过张拉吊索逐渐将主梁自重转换到主缆上,实现全桥的体系转换,在吊索张拉过程中主缆几何非线性突出,吊索索力相互影响,过程控制难度大[1]。体系转系既是自锚式悬索桥的施工难点,又是施工监控的关键工作。该文以一座主跨150m的双塔自锚式悬索桥为背景,对该工程中所做的体系转换施工监控实践研究工作进行总结。
1 工程概况
该文所研究的双塔自锚式悬索桥全长294m,跨径组成为(32+40+150+40+32)m,矢跨比为1/5.3,全桥共设2根平行钢丝主缆,主跨侧设28对镀锌高强钢丝吊索,主跨采用钢-混叠合梁,边跨及次边跨采用预应力混凝土连续箱梁,主塔及边墩上设约束横向位移的支座及纵向阻尼器,桥型立面布置如图1所示。
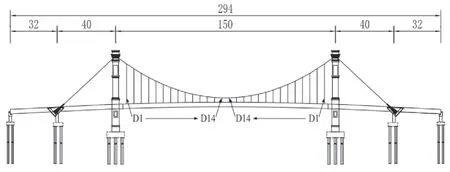
图1 桥型立面布置图(单位:m)
大桥总体采用“先塔梁同步施工、再挂设主缆、最后张拉吊索(体系转换)”的施工工序,在吊索张拉完成后大桥完成体系转换。该文针对在大桥体系转换过程中的主缆挂设控制、索夹定位及安装复核、吊索张拉及索鞍顶推、二轮调索等施工监控要点进行总结。
2 有限元仿真分析计算
该文先基于无应力状态法[2],根据设计基础参数和实测数据,采用有限元软件MIDAS CIVIL建立仿真计算的成桥状态模型,其中主梁、桥塔均采用空间梁单元模拟,主缆、吊索采用索单元模拟,边墩及次边墩实际支承条件采用一般支承模拟,计算模型如图2所示;再通过倒装分析法确定空缆线形;最后以空缆状态作为初始状态,通过正装分析法对大桥体系转换过程进行仿真分析,确定体系转换过程中的关键理论参数。

图2 全桥有限元分析模型
3 主缆挂设控制
通过有限元分析可计算出主缆中心索股的无应力长度,再根据锚端及主索鞍处主缆的空间位置分布对各索股的无应力长度进行精细化计算,确定主缆各索股的下料长度[3]。
当主缆挂设时,以底缘的索股作为基准索股,考虑现场实际温度与设计基准温度偏差对主缆垂度的影响[4],以主、边跨的跨中垂点为控制测点进行主缆挂设控制。在基准索股架设完成后,分别在主、边跨的跨中垂点处布设自动化温度传感器(图3),并采用测量机器人,以每小时1次的监测频率同时测量基准索股垂点高程及温度变化;分析连续72h监测数据,在确定中、边跨垂点高程与温度的实际相关性后,对基准索股的垂点定位进行再次调整。采用与相邻索股“若即若离”的原则,完成其余一般索股的挂设。在紧缆后,测量复核主缆中跨垂点高程,实测高程与理论高程偏差仅为3mm。

图3 自动化温度传感器布置图(单位:m)
4 索夹定位及安装复核
主缆的大位移效应导致索夹安装前须先在空缆状态下在主缆上放样标记全部索夹的安装位置,方便准确安装索夹。该文先计算出索夹从空缆状态到成桥状态的累计纵向、横向位移,再将索夹的成桥状态坐标与累计位移相减得到设计基准温度下的空缆索夹定位坐标;在实际索夹位中还需要现场实际温度与设计基准温度间的差异来对索夹定位坐标进行温度修正。现场实际索夹定位坐标如公式(1)所示。
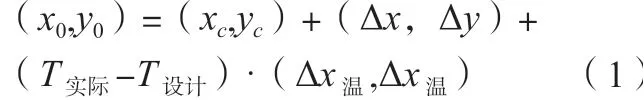
式中:x0、y0为空缆状态下索夹纵向、横向定位坐标;xc、yc为成桥状态下索夹纵向、横向位置坐标;∆x、∆y为空缆状态到成桥状态的累计纵向、横向位移;T实际、T设计分为现场实际温度和设计基准温度;∆x温、∆y温为每升温1℃空缆状态下索夹的位移变化。
在索夹全部安装后须再次测量复核索夹实际安装位置,纠正放样、安装的偏差。索夹安装后的理论位置可通过计算空缆状态到索夹安装后的位置变化和温度偏差修正来得到。经过复核和纠偏,背景桥索夹安装后的纵向实际坐标与理论坐标偏差为-11mm~12mm,横向实际坐标与理论坐标偏差为-2mm~2mm,位置偏差满足设计文件的相关要求。
5 吊索张拉及索鞍顶推
5.1 吊杆张拉及控制原则
吊索张拉是自锚式悬索桥体系转换中最关键的施工步骤,通过分批张拉吊索,将主跨主梁质量通过吊索传递至主缆,再经由主缆传递至索塔及边跨主梁。根据结构受力和施工特点,吊索张拉及控制应遵循以下原则:1)应确保整个过程中吊索的强度安全系数满足《公路悬索桥设计规范》(JTG/T D65—05—2015)[5]中的相关要求。2)在吊索张拉过程中,塔顶索鞍处于锁定状态,为平衡索鞍两侧主缆水平力,索塔塔身弯矩逐渐增大,须在适当的时机进行索鞍顶推,释放塔身弯矩或预存一定的反向弯矩来避免塔身开裂[6]。3)随着吊索张拉,主缆在索鞍处产生的竖向力将逐渐增大,索鞍与底板间的摩阻力也逐渐增大,索鞍顶推宜尽早进行。4)应确保主梁在整个过程中的受力安全。5)张拉方案宜依序连续作业,尽量减少设备投入量和设备搬移次数。6)吊索控制“以无应力长度控制为主、以索力控制为辅”。
5.2 吊索张拉方案
根据前述吊索张拉及控制原则,结合现场施工条件,采用4套200t张拉设备,按D14吊索至D1吊索的顺序进行逐对吊索挂设和张拉,具体张拉方案见表1。

表1 吊索张拉及索鞍顶推控制表
5.3 索塔塔身受力分析
根据表1的张拉方案,以索塔的塔根以及塔梁交界处较为薄弱的截面作为控制截面进行受力分析,分析结果如图4所示。分析结果表明,吊索张拉过程中,索塔控制截面的最大拉应力为1.82MPa,最大压应力为6.13MPa,未超过塔身C50混凝土的抗压强度设计值和抗拉强度设计值;在吊索张拉完成后,索塔控制截面未出现拉应力,塔身受力状态合理。

图4 吊索张拉过程中索塔控制截面最大、最小应力图
5.4 吊索索力分析
由表1的张拉方案可知,每根吊索均以锚头拔出量控制为主,一次将吊索张拉到位。经有限元计算分析,随着吊索逐对张拉,临时支墩所承受的中跨主梁自重逐步向主缆转移,当完成D7吊索张拉后,中跨主梁开始逐渐脱架;但在主梁逐渐脱架的过程中,由于分担主梁自重的吊索数量少于体系转换完成后的吊索数量,部分吊索的索力值较大,甚至可能超过其设计承载能力限值,因此需要计算吊索张拉过程中各吊索的最大索力,确保其强度安全系数满足设计要求。吊索张拉过程中各吊索的最大索力值和强度安全系数如图5所示,D1~D14吊索的最大索力为1819kN,D1~D14吊索的最小强度安全系数为2.0,满足《公路悬索桥设计规范》中施工过程强度安全系数不小于1.21的要求。
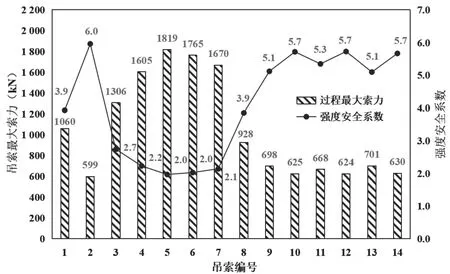
图5 吊索张拉过程中各吊索最大索力值
6 二轮调索
受到上下锚点位置偏差、吊索张拉偏差等影响,第一轮吊索张拉后的桥梁实际状态与理论状态存在一定偏差,需要通过二轮调索使桥梁的实际状态尽量逼近理论状态。根据实际施工情况,背景桥的二轮调索步骤如下:1)在第一轮张拉后,先对主梁线形、主缆线形以及吊索索力等重要控制指标进行通测复核,找出偏差并分析偏差形成的原因。2)通过有限元分析确定每根吊索索力间以及每根吊索索力与主梁线形间的影响矩阵。3)以主梁线形平顺、吊索索力合理为控制目标,利用影响矩阵法[7],通过调整最少数量的吊索来完成桥梁状态调整。4)在调索完成后,对主梁线形、主缆线形以及吊索索力等进行再次通测复核,若偏差满足设计要求,则二轮调索完成,若偏差未能满足要求则重复2)~4)直至满足要求。
经二轮调索后,背景桥中跨主梁线形平顺,实测线形与理论线形偏差为-4mm~11mm;长吊索D1~D9的实测索力与理论索力偏差为-9.4%~9.9%;左、右幅主缆中跨跨中垂点高程偏差分别为-18mm、-19mm,满足设计文件中垂点高程偏差不大于±20mm的要求。二轮调索达到预期目标。
7 结语
该文基于无应力状态法来建立背景桥的有限元成桥模型,通过倒拆分析法确定空缆状态,再以空缆状态为初始状态通过正装分析法对大桥体系转换过程进行仿真分析。该文通过自动化温度传感器及测量机器人经72小时连续监测后确定了基准索股垂点高程和温度变化的实际相关性,紧缆后的中跨垂点实测高程与理论高程偏差仅为3mm。该文介绍了考虑温度修正的索夹放样坐标及安装后坐标的计算方法,经复核、纠偏后,索夹安装位置偏差满足设计要求。该文介绍了吊索张拉及控制原则,并根据该原则制定了吊索张拉方案;针对该方案对吊索张拉过程中的塔身受力和吊索索力进行计算分析,在体系转换过程中塔身控制截面最大拉、压应力未超过其设计值,在体系转换后塔身控制截面未出现拉应力,吊索索力的施工过程强度安全系数满足规范的相关要求。该文根据背景桥施工情况进行了二轮调索。在体系转换完成后,主梁线形平顺,吊索索力偏差小于10%,主缆中跨跨中垂点高程偏差满足设计文件要求,二轮调索达到预期目标。

