一类线性函数方程Af(x)+Bf(φ(x))=g(x)的求解补注*
石勇国 宋西泠 罗小宇
(内江师范学院数学与信息科学学院 641100) (四川省资中县球溪高级中学 641208) (内江师范学院数学与信息科学学院 641100)
在各类高中数学竞赛中,常见的一类线性函数方程形如:
Af(x)+Bf(φ(x))=g(x),
(1)
其中A,B为给定实数,f是未知函数,g为已知函数,φ是迭代周期为n的函数,这里的迭代周期是指存在最小的正整数n,使得φ自身复合n次等于本身,即对于在定义域内任意的x,有
φm(x)≠x(m=1,2,…,n-1),φn(x)=x.

本文重点探讨线性函数方程(1)在奇异情形A2-B2=0下的求解方法,并且给出实例,完整讨论了迭代周期为2的线性函数方程(1)的所有解.
1 非奇异情形下的解
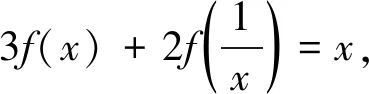

那么,对于更一般的函数方程(1),是否存在f(x)的求解公式?下面,就求解线性函数方程的方法展开说明.
定理1假设A2-B2≠0,φ是迭代周期为2的函数,则方程(1)的解为
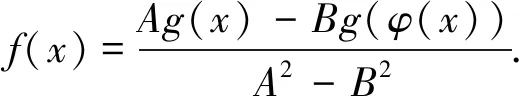
(2)
证由φ2(x)=φ(φ(x))=x,以φ(x)代换x,代入Af(x)+Bf(φ(x))=g(x),即
Af(φ(x))+Bf(x)=g(φ(x)).
与方程(1)联立并化简得
A2f(x)-B2f(x)=Ag(x)-Bg(φ(x)).
由于A2-B2≠0,因此
在定理1中,若φ(x)是一个迭代周期为2的分式线性函数,则φ必定具有如下形式
证明从略,详见文[5]和文[7].于是,方程(2)可以改写为
一般地,当φ(x)为一个迭代周期为n的函数,且An+(-1)n-1Bn≠0时,归纳可得
求解方法详见文[4].
以上所有求解方法都基于非奇异的必要条件A2-B2≠0.然而,在奇异情形A2-B2=0下,以上定理都不再适用.那么,又如何求奇异情形下方程(1)的解呢?
2 奇异情形下的解
在方程(1)中,当A2-B2=0时,不妨假设A=B=1,或A=1且B=-1,并考虑最简单情形g(x)=0时方程(1)的解.
引理1设φ(x)是迭代周期为2的函数,A=B=1,则线性函数方程f(x)+f(φ(x))=0的解形如f(x)=h(x)-h(φ(x)),其中h为任意函数.
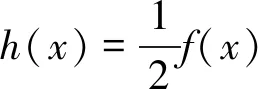
f(x)=h(x)-h(φ(x)).
引理2设φ(x)是迭代周期为2的函数,A=1且B=-1,则线性函数方程f(x)-f(φ(x))=0的解形如f(x)=h(x)+h(φ(x)),h为任意函数.

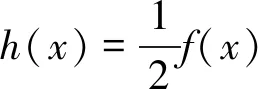
f(x)=h(x)+h(φ(x)).
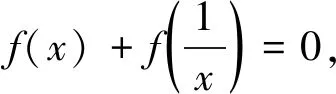

由表2可知,各处理组合对粗糠树出苗率的影响差异很大,混沙沤制,12月15日播种,露地低床播种(处理5)的出苗率最高,为92.51%。


进一步地,讨论g(x)≠0时,方程(1)有解的必要条件,以及求解方法.
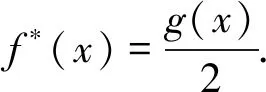
证明用φ(x)代换x,得到新方程f(φ(x))+f(x)=g(φ(x)),而由原式f(x)+f(φ(x))=g(x),故g(x)=g(φ(x)).

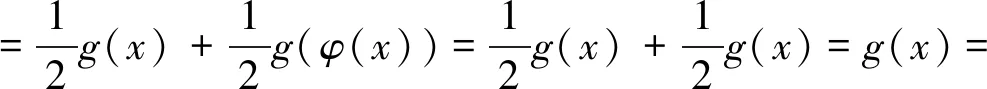
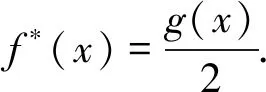
证明用φ(x)代换x,得到新方程f(φ(x))-f(x)=g(φ(x)),又由原式f(x)-f(φ(x))=g(φ(x)),则g(x)=-g(x).

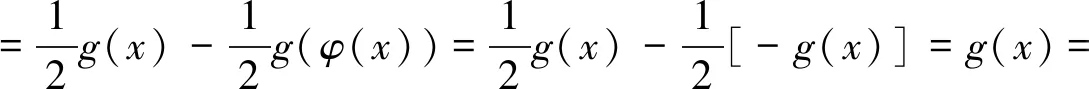
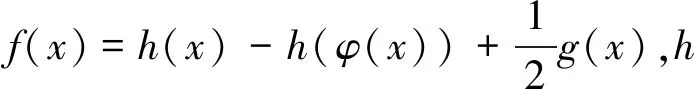
证明因为f(x)=g(x)-f(φ(x)),则有2f(x)=f(x)+f(x)=f(x)+g(x)-f(φ(x)),即
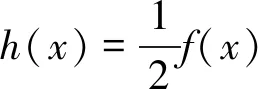
类似地,可以证明:
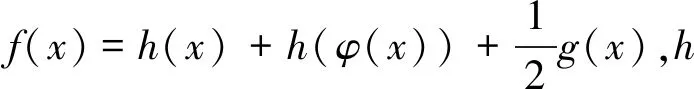
证明因为f(x)=g(x)+f(φ(x)),则有2f(x)=f(x)+f(x)=f(x)+g(x)+f(φ(x)),即
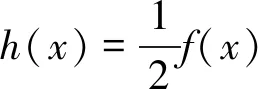
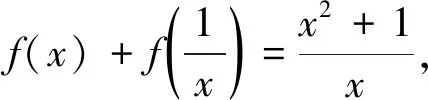

再由定理2,方程的一般解形如:
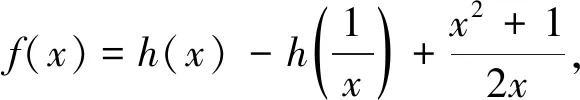
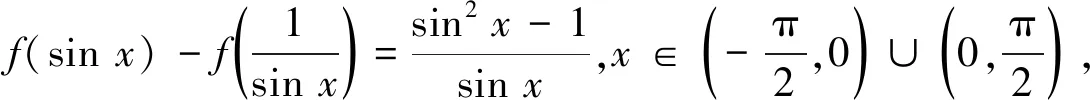
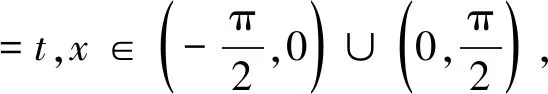

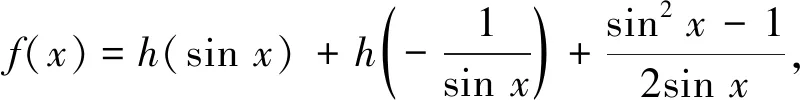
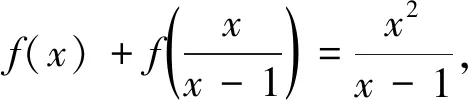

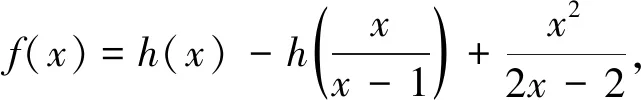
3 总结
本文针对一类线性函数方程Af(x)+Bf(φ(x))=g(x),其中φ(x)是迭代周期为2的函数,提供了通用的求解方法,补充探讨了这类线性函数方程在奇异情形A2-B2=0时解的性质以及求解的方法,并设计了实际例子以作参考.类似本文方法,可以继续研究φ(x)的迭代周期为3,4,5,…,n时该线性函数方程的解.

