Detecting the meteoroid by measuring the electromagnetic waves excited by the collision between the hypervelocity meteoroid and spacecraft

Bo LIU(刘博),Heng ZHANG(张恒),Bin XU(徐彬),Zhengzheng MA(马征征),Hui LI(李辉) and Wenshan DUAN(段文山),*

1 College of Physics and Electronic Engineering,Northwest Normal University,Lanzhou 730070,People's Republic of China

2 National Key Laboratory of Electromagnetic Environment(LEME),China Research Institute of Radio Wave Propagation,Qingdao 266107,People's Republic of China

Abstract The electromagnetic pulse excited by the collision between a hypervelocity meteoroid and a spacecraft is studied both numerically and theoretically.It is found that there are two kinds of electromagnetic pulse.The high-frequency electromagnetic pulse may be excited by the sum of all the electric dipoles.Each electron can be considered as an electric dipole.The low-frequency electromagnetic pulse is produced by the Langmuir oscillation of electrons.The energy flux density and the duration time of the excited low-frequency electromagnetic pulse by the meteoroid are also studied in the present paper.It is shown that the energy flux density increases as either the impact speed or the mass of the meteoroid increases.It is also shown that the duration time decreases as both the impact speed and the mass of the meteoroid increase.By measuring the strength and the duration time of the electromagnetic pulse excited by the collision between the hypervelocity meteoroid and spacecraft,we can estimate the speed and the mass of the hypervelocity meteoroid,which will be helpful in space flight and space exploration.

Keywords:plasma,electromagnetic pulses,hypervelocity impact,PIC simulation

1.Introduction

Spacecraft are routinely bombarded by interplanetary dust particles,called meteoroids[1-4].A meteoroid is a small,solid,extraterrestrial object in the size range of 100 μm to 10 m.It usually has an impact speed up to 72 km s-1.Particles smaller than this are called dust,while those larger than this are called asteroids[5,6].The vast majority of detected meteoroids mainly originate from comet and asteroid debris streams within our solar system,while a small portion possibly come from the outside of our solar system.Meteoroids travelling at high speed frequently impact spacecraft and cause different kinds of damage.An approximate satellite impact rate has been detected previously[3,7].It is estimated that particles smaller than a microgram routinely hit most spacecraft.Hypervelocity meteoroids may cause not only mechanical damage,but also electrical damage.Usually,the larger meteoroids(＞120 μm)mainly cause mechanical damage[8],while the smaller ones mainly cause electrical damage[9].

When the meteoroids impact with the spacecraft,they can ionize and vaporize themselves as well as a significant portion of the spacecraft material,which will form a plasma[10-12].Simultaneously,the plasma rapidly expands into the surrounding vacuum because of its high kinetic energy[13,14].Under certain conditions,this plasma can trigger electromagnetic pulses(EMPs)that may disable or destroy spacecraft electronics and,in the worst case scenario,result in complete loss of mission[5,7,15-17].Previous reports show that spacecraft usually experience electrical anomalies correlated with meteoroid showers[18-32],while few works have reported on the damage to satellite electronics through these processes.We will focus on the electrical effect associated with a meteoroid impact in the present work,especially the EMP,excited by the collision between a hypervelocity meteoroid and a spacecraft.Dependence of the energy flux density and the duration time of the electromagnetic wave excited by collision on both the speed and the mass of the meteoroid is given in the present paper.It seems that by measuring the strength and the duration time of the electromagnetic wave excited by the collision,we can estimate the speed and the mass of the hypervelocity meteoroid,which may be helpful in the aerospace industry.

2.Model

To understand the electrical damage to a spacecraft caused by the impact of hypervelocity meteoroids,we now study an expanding plasma composed of electrons and singly charged ions.We neglect the negative ions and dust particles as well as the multi-ion ionization possibly produced by the impact because all of these effects are so weak that they are negligible[33].The neutrality condition isne0=ni0,wherenα0are the initial number densities of the species α,with α=e,i denoting the electron and ion,respectively.We also assume thatTe=Ti,whereTαis the temperature of the species α.Although there are some differences in temperature between ions and electrons,the thermal velocities may be considerably different.The thermal velocity of electrons is generally much larger than that of ions;therefore,we neglect the thermal motion of ions.

For simplicity in the calculation,we assume that the plasma is initially in the hemisphere,as seen in figure 1,while outside the plasma it is a vacuum.Because of the density gradient,the plasma will expand to the vacuum.Then,the EMP may be excited during the expansion of the plasma because of the accelerated motion of the charged particles.To understand this problem,we have to understand the following phenomena:(1)the charge generated by the impact,and(2)the penetration depth of the formed plasma.

First,the total charge generated by the impact can be estimated using ground-based measurements of hypervelocity impacts on various dielectric materials[5]:

whereqis the total charge in C,mis the meteoroid mass in g,andvis the meteoroid impact speed in km s-1[34].There are many variations of equation(1)published in the literature[28,35-38]with speed exponents that range between 2.5 and 4.5 while,in the present work,we use 3.1.

Second,the penetration depth of the formed plasma we will use in the present paper is given by Frost[30],which is in a relatively thick metal plate

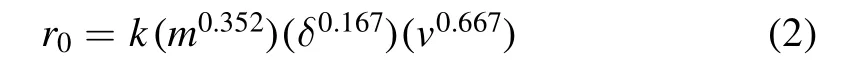
wherer0is the penetration depth in cm,kis an empirically determined target material constant(0.42 for aluminum)and δ is the density of the meteoroid in g cm-3(assumed to be 1 g cm-3).It is noted from equation(2)thatkis different for different materials of the structure of the spacecraft.Furthermore,δ is also different in the different meteoroids.Therefore,the plasma region produced by the impact is different for either the different materials of the spacecraft or the different meteoroids.Then,the power of the electromagnetic waves is different for either the different materials of the spacecraft or the different meteoroids.

We assume that the ionization process of the vaporized impact constituents has been described as 100 percent single ionization when the meteoroids impact with the spacecraft,because we only consider such a short period that the recombination during this period is negligible[13].As plasma is formed,it will rapidly expand into the surrounding vacuum,i.e.both the electrons and ions of the plasma will be accelerated.The equations of the motion of both the electrons and ions for our system satisfy the following equations

where ϵ0is the permittivity of free space,μ0is the permeability of free space,E is the electric field,B is the magnetic field,J is the current density,vαis the velocity of the species α,andmαis the mass of the species α.

We employ PIC simulations with two spatial and three velocity dimensions.The size of the simulation area is 12 μm×12 μm and 2000×2000 grid nodes are chosen.The PIC simulation diagram is shown in figure 1.We can also choose the different simulation areas;however,the results will be similar.We choose 2000×2000 grid nodes,which result in the fact that the grid width is approximately equal to the Debye length.This ensures that the PIC grid length limitation is satisfied.The regionx＞0 is the vacuum,the regionx＜0 is the spacecraft region and the hemisphere represents the initial plasma region.We assume that there is no external magnetic field since the Earth’s magnetic field is small enough.We also neglect the Coulomb collisions in the present work.It can be verified that Coulomb forces between charged particles are much lower than the thermal forces at the initial stage of the impact by using the plasma parameters given in the present paper.

The initial conditions in the simulation are as follows:the plasma is uniformly distributed in the hemisphere,E0=0,B0=0,J0=0,ve0=vthe,vi0=vthi,wherevthαis the thermal velocity of the species α.

We use the absorptive boundary conditions on all sides for fields and particles,though in simulation the particles never approach the boundary.

In PIC simulations,the finite-difference time-domain(FDTD)method has been employed as a standard numerical solver for the Maxwell equations.The FDTD method is simple and flexible,but its use has been known to result in the phase speed of the electromagnetic wave being numerically less than the speed of light in high-wavenumber regions because of the finite size of spatial cells and time steps.This numerical dispersion induces a nonphysical numerical instability that is now known as numerical Cherenkov radiation[39-43].Several methods have been developed to suppress the numerical instability.One method applies digital filtering to waves in high-wavenumber regions.In our simulation,the spatial filtering(erasing electromagnetic fields of particularly short wavelengths)and temporal filtering(erasing‘suspected noise’signals whose period is only two or three time steps)have been used.This greatly eliminated the numerical instabilities.It has recently been reported that careful choices of the Courant-Friedrichs-Lewy(CFL)number can greatly inhibit growth of the numerical Cherenkov instability[44].In our simulation,we also have chosen the suitable CFL conditions,which greatly inhibited the numerical instabilities.

The meteoroid parameters in the present paper are given as follows:the mass of the meteoroid is 10-15g,and the velocity of the meteoroid is 56 km s-1[5].Larger mass meteoroids can also be studied,similar to that in the present paper.The procedure to study the other meteoroids is the same as that in the present paper.Then,both the corresponding initial density and the initial radius of the plasma can be obtained from equations(1)and(2)as follows:ne=3.298×1025m-3andr0=3.23×10-7m.The temperatures of both ions and electrons areTe=Ti=2.5 eV,and then we have the following parameters:the thermal velocity of electrons isvthe=6.6×105m s-1,the thermal velocity of ions isvthi=3×103m s-1and the initial expansion velocity of the electrons isvexpansion=5.6×104m s-1.

3.Results

Figure 2 show the variations of the excited electric field and the magnetic fieldEx,Ey,Ez,Bx,By,Bzwith respect to timetat the fixed points(the distance between this point to the center of the plasma is 400 nm)with different angles θ=0°,45°;the results for other angles are qualitatively the same as those of these special angles(the angle is between the positivexdirection and the vector from the center of the plasma to the considering point).It is observed in figure 2 that there are two different electromagnetic oscillation models.The first is the components ofBx,By,Ez.The second is those ofEx,Ey,Bz.It is found that both wave amplitudes decay with timet.However,the decaying rates are different between the two modes.In the following sections,we will investigate these two different electromagnetic oscillation modes in more detail.

Figure 1.A schematic diagram of the particle-in-cell(PIC)simulation region.The simulation area is 12 μm×12 μm,the region x＞0 is the vacuum,the region x＜0 is the spacecraft region and the hemisphere represents the initial plasma region.

Figure 2.The variations of quantities of(a)-(c)Bx,By,Bz and(d)-(f)Ex,Ey,Ez with respect to time t at the fixed points at which the distance between this point and the center of the plasma is 400 nm with different angles θ=0°,45°(θ is the angle between the positive x direction and the vector from the center of the plasma to the considering point),where ne=ni=3.298×1025 m-3,r0=3.23×10-7 m,and Te=Ti=2.5 eV.

Figure 3.The variations of quantities of Bx,By and Ez with respect to time t at the fixed points at which the distance between this point and the center of the plasma is 400 nm with the angle θ=0°are shown in(a),(b)and(c);the corresponding frequency spectra are shown in(d),(e)and(f).Here,ne=ni=3.298×1025 m-3,r0=3.23×10-7 m,and Te=Ti=2.5 eV.

3.1.High-frequency EMP model

It is noted in figure 2 that the decaying rates of the first modes ofBx,ByandEzare larger than those of the second modes,Ex,EyandBz.To gain more insight into the first kind of oscillations of the quantities ofBx,ByandEz,the variations ofBx,ByandEzwith respect to timetin a shorter period are given in figures 3(a)-(c).It seems that the amplitude ofByis about 10 times that ofBx.It suggests that the wave propagates in the positivexdirection.

We now try to understand how this electromagnetic wave is produced during this process.First,the plasma is produced by the impact of the hypervelocity meteoroid.Then,the plasma will expand to the vacuum because of the intense density gradient.Because any accelerated charged particles can excite the electromagnetic waves,the electromagnetic wave is then excited due to the acceleration of the electrons.For simplicity,we approximately assume that each accelerated electron is an electric dipole,whose frequency is just the electron collision frequency.Therefore,the excited high-frequency electromagnetic wave in our system can be considered by the sum of the many electric dipole radiations,as suggested in previous works[5,45].

3.1.1.The radiation power excited by the accelerated electron.We now need to verify the prediction that the electromagnetic wave is the sum of all the electric dipole radiations.It is supposed that there areNeelectrons that excite the electromagnetic wave.We first consider an arbitrary electron(jth electron,j=1,2,…,Ne).Then,the electric field,the magnetic field and the radiation power of thejth accelerated electron are given by[46]

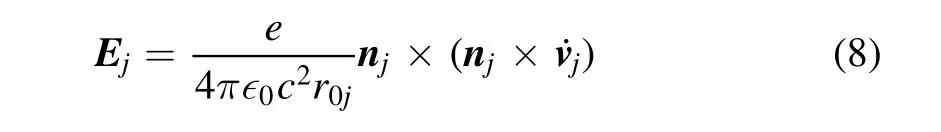
3.1.2.Frequency of the high-frequency EMP.The frequency of this high-frequency EMP can be estimated by assuming that each electric dipole radiation of an electron is a simple harmonic oscillation,wheredeis the mean distance between the electrons,is the mean velocity of thejth electron,ωjis the vibration frequency of thejth electron and δj1is the initial phase of thejth electron.Then,the acceleration of thejth electron isAlthough,the frequencies are different for different dipoles,we can estimate the mean frequency of the high-frequencywhich is in the same order as the numerical result.However,it seems that our theoretical results are a little smaller than those of the numerical results.This is possibly because the electric dipole of an electron is not a simple harmonic oscillation.In fact,there are higher frequency harmonic oscillations.

It is noted that there are many higher harmonic EMP frequencies excited by the electric dipole radiation,nω0(n=1,2,…),which gives a reasonable explanation that there are some higher EMP frequencies in our numerical results,and it almost in agreement with the results in figures 3(d)-(f).

3.2.Lower-frequency EMP model

Figures 4(a)-(c)show the variations of the componentsEx,Ey,Bzof the electromagnetic wave with respect to timetat the fixed points(the distance between this point to the center of the plasma is 400 nm)with the angle θ=45°.It is observed from figures 4(a)-(c)that the components ofEx,Ey,Bzoscillate with timet,while their amplitudes decrease with time.

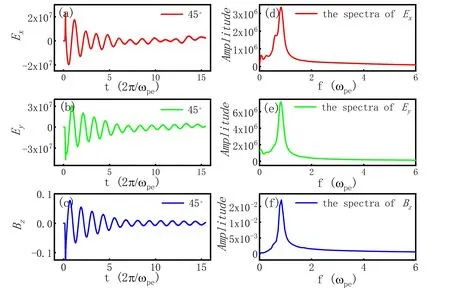
Figure 4.The variations of quantities of Ex,Ey and Bz with respect to time t at the fixed points at which the distance between this point and the center of the plasma is 400 nm with angle θ=45°are shown in(a),(b)and(c).The corresponding frequency spectra are shown in(d),(e)and(f).Here,ne=ni=3.298×1025 m-3,r0=3.23×10-7 m,and Te=Ti=2.5 eV.

Figure 5.The variations of the frequency of the low-frequency electromagnetic wave with respect to both the impact speed and the mass of the hypervelocity meteoroid,where(a)m=10-15 g and(b)v=56 km s-1.

3.2.1.Frequency of the low-frequency EMP.It seems that the frequency of the lower-frequency electromagnetic wave is nearly constant.To verify this estimation,we presented the frequency spectra ofBz,EyandExin figures 4(d)-(f),respectively.It is observed that there is only one main frequency for these electromagnetic waves.Furthermore,the dependences of the main frequency on both the impact speed and the mass of the hypervelocity meteoroid are shown in figures 5(a)and(b).

It seems that this main wave frequency is close to the Langmuir wave frequencyof the system,wherene0is the density of the electrons of the system.It is noted that the theoretical results are in agreement with the numerical results.Therefore,this suggests that this low-frequency electromagnetic wave is excited by the Langmuir vibration of the electrons.Figure 4 shows that the strength of the electromagnetic wave produced by the impact is the strongest at the initial time.Its strength decreases with the time.This electromagnetic wave is produced by the vibration of the electrons.The frequency of this electromagnetic wave depends on the mass and the number density of the electrons.Therefore,we can estimate the number density of the electrons at the initial time by measuring the frequency of this electromagnetic wave.Based on the dependence of the main frequency on both the impact speed and the mass of the hypervelocity meteoroid in figure 5,we can also estimate the impact speed and the mass of the hypervelocity meteoroid.

Figure 6.The variations of the energy flux density of the electromagnetic wave with respect to both the impact speed and the mass of the hypervelocity meteoroid,where(a)m=10-15 g and(b)v=56 km s-1.

Figure 7.The variations of the duration time of the electromagnetic wave with respect to both the impact speed and the mass of the hypervelocity meteoroid,where(a)m=10-15 g and(b)v=56 km s-1.

3.2.2.The variations of the excited low-frequency EMP with respect to both the speed and the mass of the hypervelocity meteoroid.We now try to understand the dependence of the energy flux density and the duration time of the excited lowfrequency electromagnetic waves on both the speed and the mass of the hypervelocity meteoroid.It seems that the energy flux density of the excited EMP strongly depends on both the impact speed and the mass of the hypervelocity meteoroid.The variations of the energy flux density of the excited EMP with respect to both the impact speed and the mass of the hypervelocity meteoroid are shown in figures 6(a)and(b).It indicates that the energy flux density increases as either the impact speed or the mass of the meteoroid increases.The approximated simulation results of the dependence of the energy flux density on both the impact speed and the mass of the hypervelocity meteoroid are as follows:

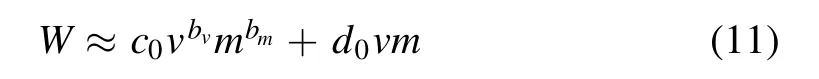
wherec0=9.03×108,bm=0.67,bv=2.84,d0=-1.035×1015,mis the meteoroid mass in g andvis the meteoroid impact speed in km s-1.Figure 6 shows that the power of the electromagnetic wave produced by the impact depends on both the impact speed and the mass of the hypervelocity meteoroid.Therefore,we can estimate the impact speed and the mass of the hypervelocity meteoroid by measuring the power of the electromagnetic wave.

As observed in figure 4,the excited EMP will attenuate with timet.Due to this reason,we define a new parameter of the duration time of the excited EMP.It is the time needed from the maximum amplitude of the excited EMP to that of 10 percent of the maximum amplitude.It is found from figures 7(a)and(b)that the duration time decreases as the speed of the hypervelocity meteoroid increases.It also decreases as the mass of the hypervelocity meteoroid increases.It seems that the duration time decreases as the energy power of the EMP increases.The approximated simulation results of the dependence of duration time on both the impact speed and the mass of the hypervelocity meteoroid are as follows:

wherea0=-5.28×10-15,b0=-0.00248,c0=5.07×10-13,mis the meteoroid mass in g andvis the meteoroid impact speed in km s-1.It is found that the duration time of the excited EMP is in the range of 1.5×10-13-5.0×10-13s.Figure 7 shows that the duration time of the electromagnetic wave produced by the impact depends on both the impact speed and the mass of the hypervelocity meteoroid.Therefore,we can estimate the impact speed and the mass of the hypervelocity meteoroid by measuring the duration time of the electromagnetic wave.

In conclusion,by measuring the electric field excited by the impact between the hypervelocity meteoroid and spacecraft,we can obtain the energy flux density.On the other hand,the duration time can be obtained at the same point.Then,by solving equations(11)and(12),we can obtain both the mass and the velocity of the hypervelocity meteoroid.These results have potential applications in space flight and space exploration.

4.Conclusion

Simulation results are presented in the present paper to study the excited EMP by the hypervelocity meteoroid.There are two types of EMP in our simulation results.The high-frequency EMP may be excited by the sum of all the electric dipoles.We assume that each accelerated electron is an electron dipole,while the effects of the ions are neglected.Agreements between our theoretical model and the numerical model are observed.The low-frequency EMP is produced by the Langmuir oscillation of electrons.We also find that the energy flux density excited by the hypervelocity meteoroid increases as either the impact speed or the mass of the meteoroid increases.The duration time of the excited EMP by the hypervelocity meteoroid is also studied in the present work.It is shown that the duration time decreases as both the impact speed and the mass of the meteoroid increase.

By measuring the strength and the duration time of the EMP excited by the collision between the hypervelocity meteoroid and the spacecraft at a certain location,we can estimate the speed and the mass of the hypervelocity meteoroid.This is potentially helpful in space flight and space exploration.To better protect our space assets and mitigate against damage,we should establish a regular space debris detection system to track and locate hypervelocity particles to effectively protect the spacecraft.Moreover,we can establish protective measures that include additional shielding or the placing of sensitive equipment at safe locations inside the spacecraft.

Acknowledgments

This work was supported by National Natural Science Foundation of China(Nos.11965019,42004131 and 42065005).