Particle-in-cell simulation of ion-acoustic solitary waves in a bounded plasma∗

Lin Wei(位琳), Bo Liu(刘博), Fang-Ping Wang(王芳平), Heng Zhang(张恒), and Wen-Shan Duan(段文山)

College of Physics and Electronic Engineering,Northwest Normal University,Lanzhou 730070,China

Keywords: ion-acoustic solitary waves,particle-in-cell simulation,bounded plasmas

1. Introduction

Nonlinear waves exist in many physical systems, such as in water,[1]optics,[2,3]and plasmas.[4-6]They have played important roles in the study of plasma physics.[7-10]They have attracted a great deal of interest because of their widely occurrence in active galactic nuclei,[11-14]pulsar magnetosphere,[15,16]solar atmosphere, and the inner regions of the accretion disks surrounding the central black holes[17-19]in the past few decades. Many authors pay attention to nonlinear waves, especially ion-acoustic solitary waves (IASWs), due to their importance in modern plasma physics.[20-22]IASWs have been theoretically and experimentally studied in various laboratory and space plasmas.[23-32]

Many researchers have investigated the characteristics of IASWs described by both the KdV equation and the nonlinear Schr¨odinger equation (NLSE) to study the phenomenon observed in various laboratory and space plasma applications.[33-40]On the other hand, a large number of numerical simulation studies have been done for IASWs by using PIC method to check the theoretical results.[41-44]For instance,Kakad et al.[42]have studied the characteristics of the ion-acoustic solitons such as amplitude, width and speed by both fluid and PIC simulations. They found that PIC and fluid results are almost consistent with small amplitude initial density perturbations. Qi et al.[43]have investigated the head-on collision between two IASWs by using the PIC simulation method in a plasma containing hot electrons and cold ions,and it is found that the PIC results are reliable if the amplitudes of both the colliding solitary waves are small enough. Sharma et al.[44]have studied the formation and propagation of large amplitude ion-acoustic solitons using a one-dimensional PIC method,and it suggests that when Mach numbers are low,the PIC simulation results are in close agreement with the KdV soliton solutions.

Although IASWs have been studied extensively by both theoretical and numerical methods, most of these studies are for unbounded plasmas. However, the plasmas in the laboratory are usually bounded in finite geometry. Studies of IASWs in a bounded plasma are meaningful because of its importance in laboratory experiments and industrial applications. Some theoretical studies have been done for solitary waves in bounded plasmas,[45-49]such as KdV solitary waves,etc.Following these theoretical works,we study not only KdV solitary waves, but also dark envelope solitons in a bounded plasma by using the PIC simulation method and considering dissipation effects of the plasma fluid. Our intention in the present paper is to verify the analytical results by PIC numerical simulation.Using the reductive perturbation technique,we obtain a modified-KdV equation and a modified-NLSE to describe the damping IASWs.We also investigate how the cylinder radius and the viscosity coefficient of the plasma affect the characteristics of IASWs.

The layout of this paper is as follows: The analytical study on the IASWs by using the reductive perturbation method is given in Section 2. In Section 3, we introduce the PIC simulation method. The PIC simulation results and the analytical ones are both discussed and compared in Section 4.Finally,our discussion and conclusion are given in Section 5.

2. Basic equations

We consider a two-component electron-ion plasma which is bounded in a finite cylinder with radius R.[45-49]Taking cylindrical coordinates,the equations of the motion of ion fluid are

where niand neare the ion and electron number densities, r,θ,and x are the radial,polar angle,and axial coordinates,t is the time. υr, υθ, and υxrepresent the components of the ion velocity in the cylindrical coordinate system. miis the mass of the ions. γ is the adiabatic coefficient, Tiis the ion temperature. ν is the viscosity coefficient of the plasma. ϕ is the electrostatic potential. nesatisfies Boltzmann distribution ne=ne0exp(eϕ/kBTe),kBis the Boltzmann constant,Teis the electron temperature.

We consider a symmetrical cylinder in the present paper.We assume that υr= υθ= 0, i.e., υx=V(r,x,t), which is usually satisfied in some special cases, such as the external magnetic field is large enough.[47,48]Under these assumptions,equations(1)-(3)can be modified as follows:

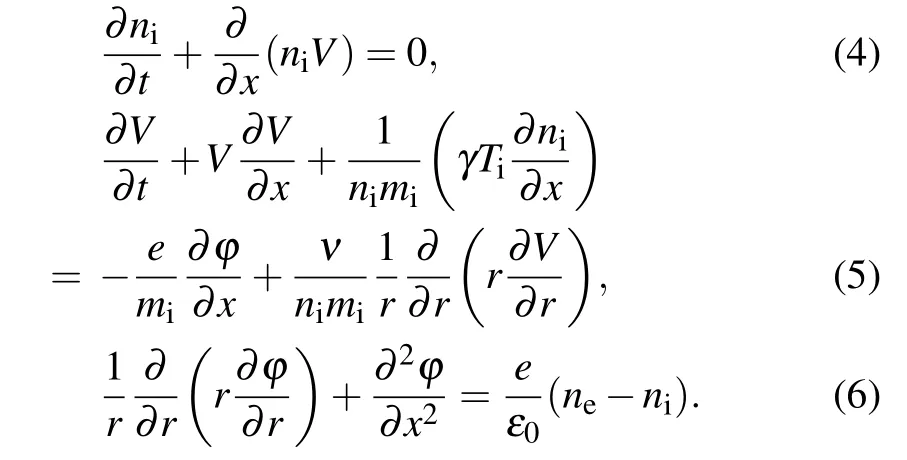
The dimen

In the following, we focus on the case that 1/k ≫R,where k is the wavenumber. Notice that in this limit, the axial and radial equations are completely independent. Accordingly,we take[45-48]

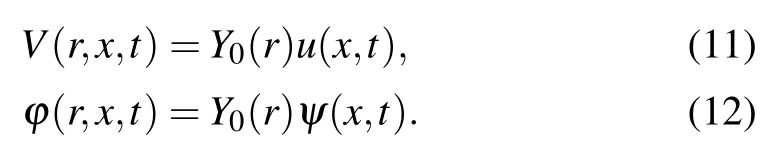
Substituting Eqs.(10)-(12)into Eq.(9),we obtain the following equations:

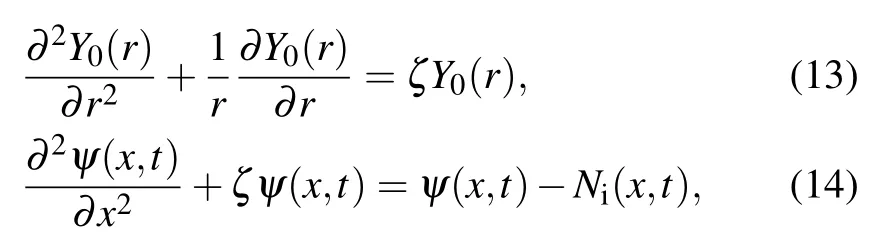
where equation (13) is a Bessel equation whose solution is a Bessel function Y0(r)=J0(βr),with ζ =−β2. ζ is the eigenvalue of Bessel equation. β will be determined by the boundary condition which will be given later.Thus,equation(7)-(9)become

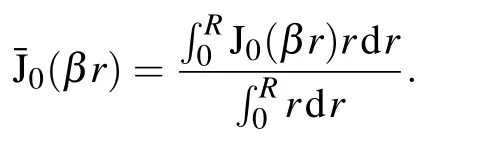
We consider the first boundary condition J0(βR)=0,i.e.,the potential at the boundary is zero.By solving the eigenvalue problem of the Bessel function,we obtain β =3π/4R. In addition,as we consider the second or third boundary conditions,only the value of β changes,the others are the same as the first boundary condition.

By averaging the physical quantities on the radial direction,we reduce the model to a one-dimensional case,in which the influence of the radius R is included in the parameter β.

2.1. Modified-KdV equation

In order to study the KdV solitary waves in a plasma,we introduce the following stretched coordinates according to the reductive perturbation technique: ξ =ε(x −ct),τ =ε3t,and ν =ε3ν0,where ε is a dimensionless parameter which stands for the strength of the nonlinearity,c is the velocity of the linear wave. Then,the dependent variables are expanded as follows:

Substituting Eq.(18)into Eqs.(15)-(17), in the first order of ε,we obtain

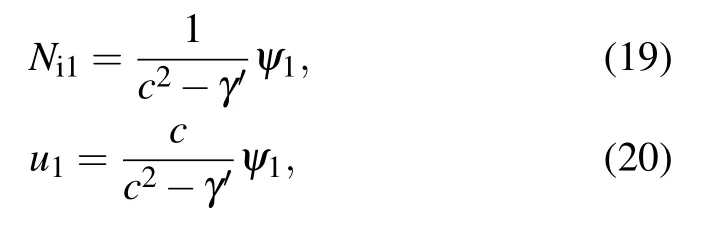
In the next higher order,we obtain the modified-KdV equation

where

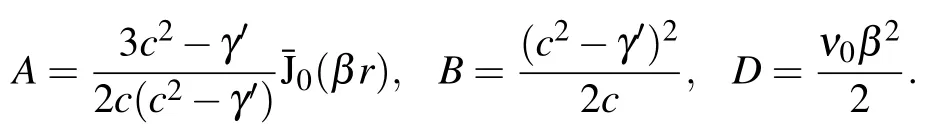
If D=0, equation (22) is a standard KdV equation, its solution is

If D/=0,equation(22)describes a damping KdV solitary wave,its approximate solution is[50,51]

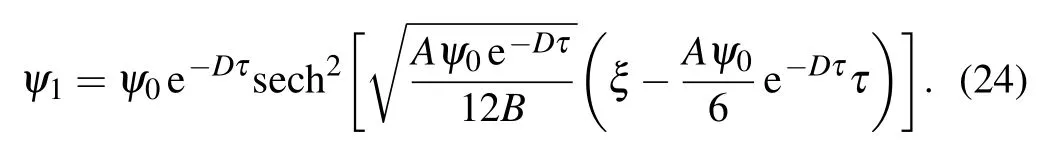
2.2. Modified-NLSE

In order to study the envelope solitary waves in a plasma,we introduce the following stretched coordinates: ξ =ε(x −υgt), τ =ε2t, ν =ε2ν0, where υgis the group velocity. All the physical quantities are expanded as follows:

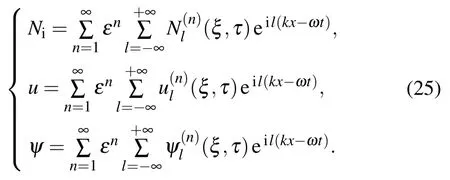
By substituting these expansions into Eqs.(15)-(17),we have the following results: the dispersion relation

the group velocity

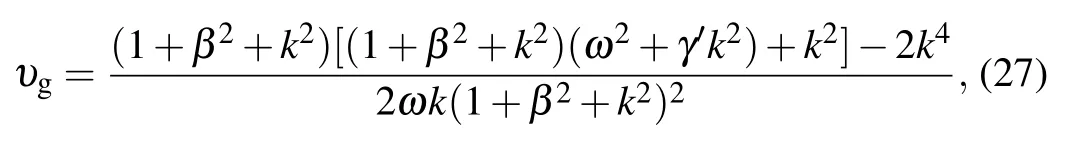
and finally the modified-NLSE

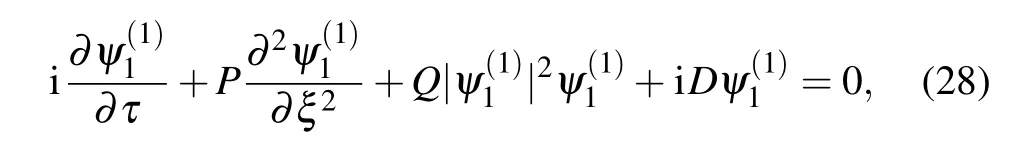
where the dispersion coefficient P and the nonlinearity coefficient Q are as follows:

the damping coefficient D is

If D=0,equation(28)is a standard NLSE.When PQ ＜0,its solution is

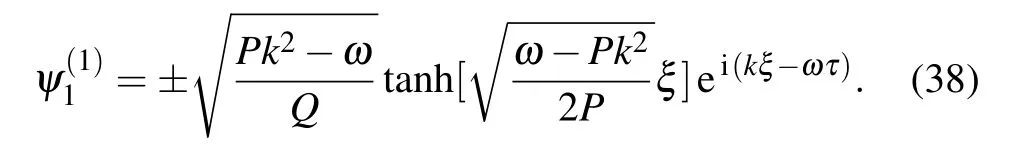
If D/=0,equation(28)is a modified-NLSE,its approximate solution(PQ ＜0)is

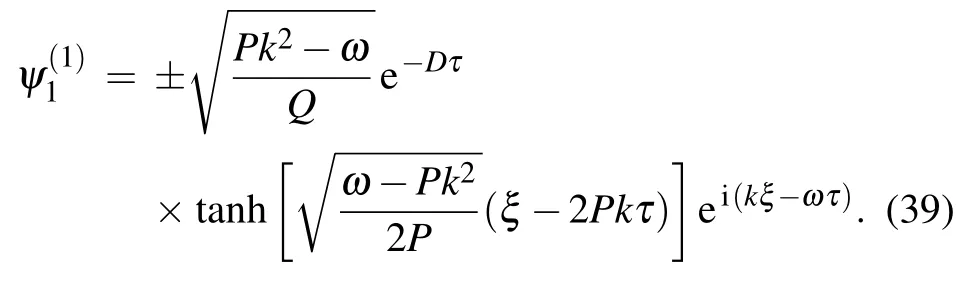
3. Particle-in-cell method

The one-dimensional PIC simulation method is applied to study the propagation of the KdV solitary waves and the dark envelope solitons in a viscous bounded plasma in this work.During the simulation, the ions are regarded as kinetic particles, while electrons are modeled as Boltzmann distributed background. Generally, real systems contain extremely lots of particles. In order to make simulations efficient, superparticles(SPs)are used. Each SP has a weight factor S specifying the number of real particles contained. The whole simulation region is divided into grid cells. At each time step, the velocities and positions of SPs are weighted to all the grids to calculate the charge density.Once the charge density obtained,the Poisson equation(electrostatic model)will be solved to derive the potential of each grid,and the electric field E at each grid is further derived. Then, each SP will be driven by the electric field, and the new position and velocity are obtained according to the motion equation. The equation of motion of the system is Newton’s equation

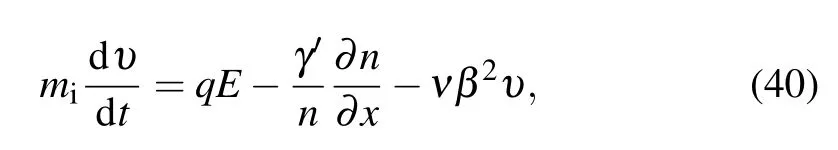
where qE is the electric field force, −(γ′/n)(∂n/∂x) is the pressure of ion fluid,−νβ2υ is the viscous force.

In addition,we need to give the value of the parameter β in the PIC simulation,which is determined by the radius of the cylinder. That is,the bounded plasma is reflected on β in the PIC simulation.

3.1. Initial condition of the damping KdV solitary wave

In the PIC simulation,initial conditions are chosen from the analytical solution expressed in Eq.(24)at t=0. The initial values of the number density and the velocity of the ions are

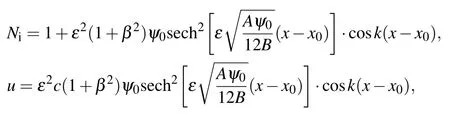
respectively. The fixed boundary conditions are used. The parameters chosen in the simulation are as follows: Δx=0.3,Δt =0.0125, the number of grid cells is Nx=10000 and the number of SPs contained per cell is 50, the total length of xaxis is Lx=ΔxNx. ε =0.2, γ′=0.003,x0=4Lx/15. This initial disturbance will evolve as the time increases.

3.2. Initial condition of the damping dark envelope soliton

In the PIC simulation,initial conditions are chosen from the analytical solution expressed in Eq.(39)at t=0. The initial values of the number density and the velocity of the ions are given below:

respectively. The boundary conditions along the x-axis are periodic. The parameters chosen in the simulation are as follows: Δx = 0.3, Δt = 0.0125, the number of grid cells is Nx=30000 and the number of SPs contained per cell is 50,the total length of x axis is Lx=ΔxNx. ε =0.01, γ′=0.003,k=0.1,x0=Lx/4. This initial disturbance will evolve as the time increases.

4. PIC simulation results

4.1. KdV solitary wave

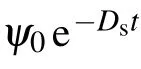
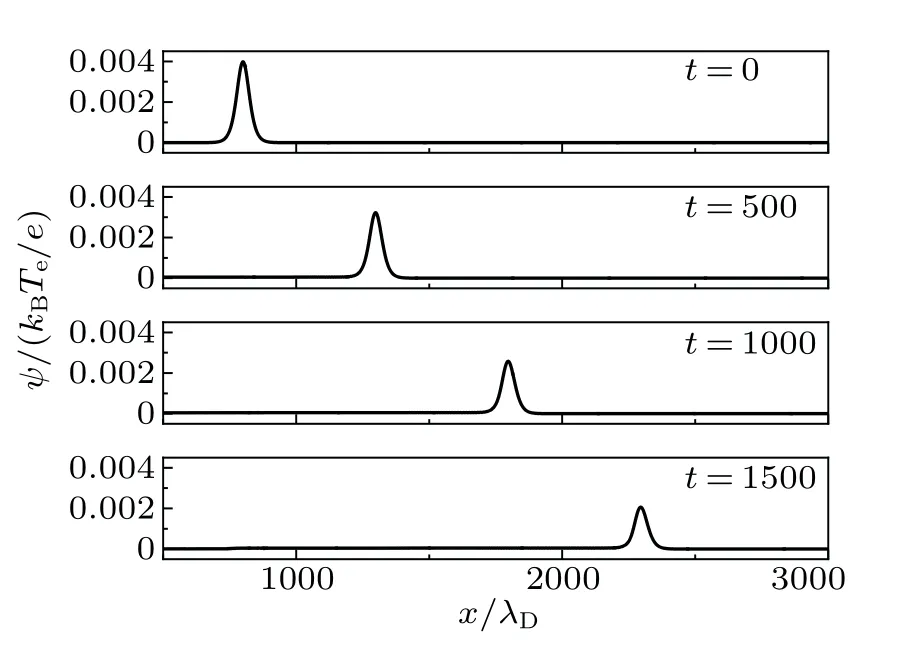
Fig.1. The PIC simulation results of the evolution of the KdV solitary wave at different time, where ε =0.2, ψ0 =0.1, γ′ =0.003, R=50, ν =0.4,D=0.056.

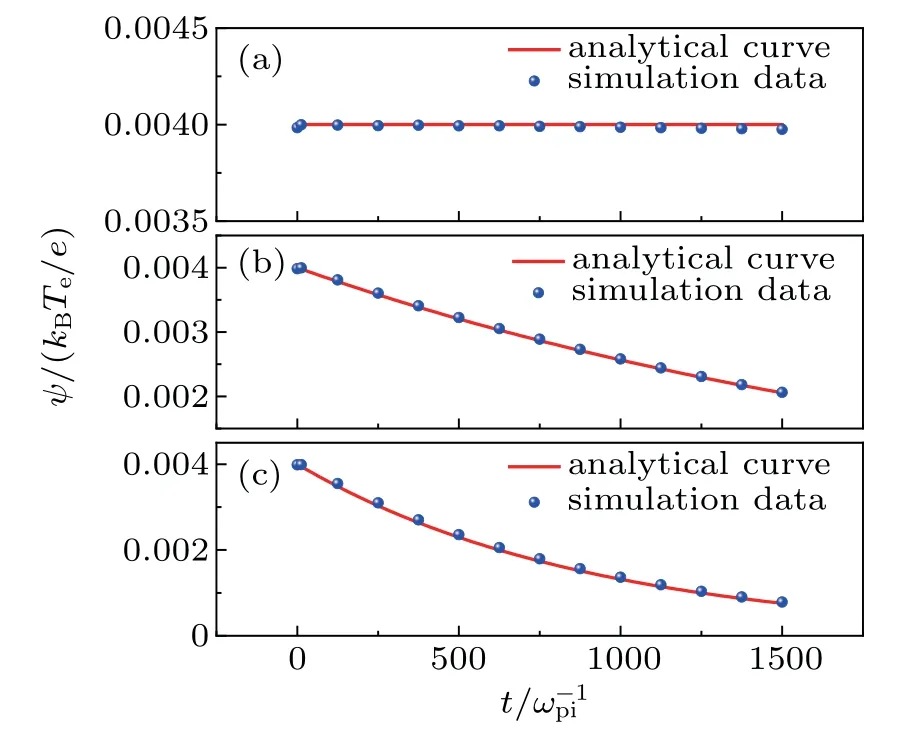
Fig.2. The dependence of the amplitude on the time for KdV solitary waves with ε =0.2,ψ0 =0.1,γ′ =0.003. (a)R=50,ν =0,D=0,Ds =0; (b)R=50, ν =0.4, D=0.056, Ds =0.053; (c)R=50, ν =1.0, D=0.139,Ds=0.134. The red lines represent the analytical results,and the blue dots represent the simulation results. Simulation results for amplitudes are compared with analytical expression (Eq. (24)) and observed that both results are in good agreement,as shown in above graph.

Furthermore, the dependence of the damping coefficient D(as well as Ds)on both the cylinder radius R and the viscosity coefficient ν is shown in Fig.3.It is noted that the damping coefficient decreases as the cylinder radius R increases,while it increases as the viscosity coefficient ν increases. It is also found that the simulation results and analytical ones are almost consistent.

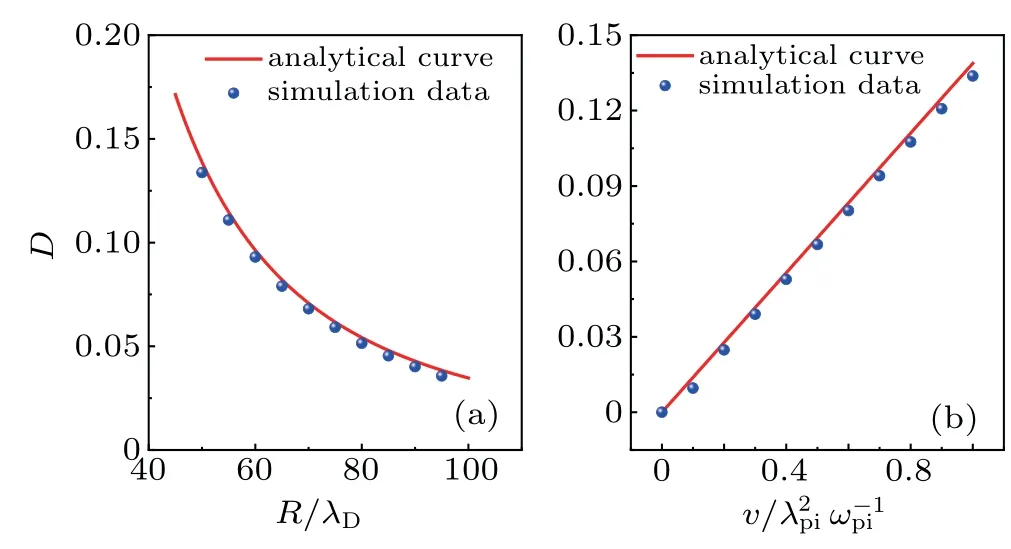
Fig.3. Comparisons of the damping coefficient between the simulation results and the analytical ones. (a) The dependence of damping coefficient D on the cylinder radius R, where ε =0.2, ψ0 =0.1, γ′ =0.003, ν =1.0;(b)the dependence of damping coefficient D on the viscosity coefficient ν,where ε=0.2,ψ0=0.1,γ′=0.003,R=50.The red lines are the analytical results,and the blue dots are the simulation results.

4.2. Dark envelope solitary wave

The evolution of the dark envelope solitary waves under the effects of the viscous force in the PIC simulation is shown in Fig.4 at different times. The initial amplitude is ψ0=0.00115. It can be observed that as time increases, the amplitude of this dark envelope solitary wave decreases. In order to get more insight into how the amplitudes of the dark envelope solitary waves attenuate,figure 5 shows the variation of the amplitudes with the time under different system parameters. Notice that when there is a viscous force,the amplitude decreases exponentially with time. We also define the same damping coefficient Dsfrom the PIC simulation as that of the KdV solitary wave. It is noted from Fig.5 that the simulation results are close in good agreement with the analytical ones,i.e.,Ds≈D. Also,it is found that the larger the damping coefficient,the stronger the attenuation of the wave.

Fig.4. The PIC simulation results of the evolution of the dark envelope solitary waves at different times, where ε =0.01, k=0.1, γ′ =0.003,R=50,ν =0.4,D=0.056.

Fig.5. The dependence of the amplitude on time for dark envelope solitary waves with ε =0.01,k=0.1,γ′=0.003. (a)R=50,ν =0,D=0,Ds=0;(b)R=50,ν =0.4,D=4.44,Ds =4.62; (c)R=50,ν =1.0,D=11.10,Ds =11.00. The red lines represent the analytical results,and the blue dots represent the simulation results. Simulation results for amplitudes are compared with analytical expression(Eq.(39))and observed that both results are in good agreement,as shown in the above graph.

Fig.6. Comparisons of the damping coefficient between the simulation results and the analytical ones. (a) The dependence of damping coefficient D on the cylinder radius R, where ε =0.01, k=0.1, γ′ =0.003, ν =1.0;(b)the dependence of damping coefficient D on the viscosity coefficient ν,where ε=0.01,k=0.1,γ′=0.003,R=50. The red lines are the analytical results,and the blue dots are the simulation results.

In order to understand how the damping coefficient depends on the system parameters, figure 6 shows the dependence of the damping coefficient D(or Ds)on the cylinder radius R and the viscosity coefficient ν.It is noted that the damping coefficient decreases as the cylinder radius R increases,while it increases as the viscosity coefficient ν increases. It is also found that the analytical results are consistent with the simulation results.

5. Discussion and conclusion

In this paper,we have studied some nonlinear waves of a viscous plasma composed of Boltzmann distributed electrons and ions fluid confined in a finite cylinder. By averaging the physical quantities on the radial direction in some cases, we reduce this system to a simple one-dimensional case. It is found that the effects of the bounded geometry(the radius of the cylinder in this case) can be included in the damping coefficient or the equivalent parameter β which also depends on what kind of the boundary condition.

Furthermore, one-dimensional PIC simulation method has been applied to study the formation and propagation of the damping KdV solitary waves and dark envelope solitary waves in a viscous bounded plasma. It is observed that the amplitudes of both the KdV solitary waves and the dark envelope solitary waves decrease exponentially as time increases.We define a damping coefficient Dsin the PIC simulation. It is found that the numerical results are in good agreement with the analytical ones, i.e., Ds≈D. The dependence of damping coefficient on both the cylinder radius R and the viscosity coefficient ν is also obtained numerically by using the PIC simulation method,which is consistent with the analytical results. It also suggests that the damping coefficient decreases as the cylinder radius increases, while increases as the viscosity coefficient increases. In the future, we will try to do three-dimensional PIC simulation in the cylindrical coordinates. Our present one-dimensional model is the result of the simplification of the three-dimensional model. We consider a symmetrical cylinder ignoring the angular motion and take the average value in the radial direction. When we only focus on the axial motion of the particles,the three-dimensional PIC simulation in the cylindrical coordinate becomes the onedimensional PIC simulation in the Cartesian coordinate. The one-dimensional model is a special case of symmetry, while the three-dimensional model is a general situation.

There are debates for a long time about whether the solitary wave exists in a bounded plasma.[52,53]Present paper tries to answer this question. We distinguish whether the solitary wave exists by the following method. We define that the solitary wave does not exist in a bounded plasma if the amplitude of the solitary wave becomes less than half of its initial value after it propagates the distance of five Debye lengths.On the other hand,the solitary wave exists in the system. By using this definition, we find a critical damping coefficient Dc=Ciln2/5λD. It seems that when D ＜Dc, the solitary wave can propagate, while it can not propagate in a bounded plasma when D ＞Dc.

Finally, our results have potential applications in laboratory experiments.[47-49]For example, if a wave is excited at one end of a finite cylindrical tube,we can detect it at the other end of the cylindrical tube in a micro-gravity condition.Therefore,the damping coefficient can be obtained by measuring the wave amplitudes at both ends of the cylindrical tube. Then the viscosity coefficient of the plasma can be indirectly obtained from the relationship between the damping coefficient and the viscosity coefficient of the plasma.