基于杜芬方程的地铁ATS 系统周期性风险反馈控制机理研究

于耀程黄文成 帅斌 张锐 许旻昊 徐逸飞

(1.西南交通大学 交通运输与物流学院,四川 成都 611756;2.西南交通大学 系统科学与系统工程研究所,四川 成都 611756;3.西南交通大学 综合交通运输智能化国家地方联合工程实验室,四川 成都 611756;4.西南交通大学 综合交通大数据应用技术国家工程实验室,四川 成都 611756)

0 引言

地铁列车ATS(automatic train supervision)系统是列车自动控制系统ATC(automatic train control)的核心功能部件之一。ATS 系统组件数多,操作复杂,这使得影响其正常运行、导致其状态发生不稳定震荡的风险因素较多,如主机服务器网络不稳定,离线、上线过程中冗余服务器之间的互相干扰,系统硬件设施老化,机房密封措施不够完善,定期设备检修不到位,人员操作失误等[1]。此外,上述风险因素的耦合协调作用也可能导致ATS 状态发生不稳定的震荡,从而导致事故的发生。若系统在运行过程中出现故障,将造成全线进路无法自动触发等严重故障,列车安全运行将受到极大阻碍,影响运营效率,严重时可能导致火灾、列车晚点、列车追尾等重大事故,造成巨大的经济损失或人员伤亡。例如,2011 年9 月27 日14:51 分,由于信号系统故障,上海地铁10 号线由豫园站至老西门站的下行区间处两列车追尾,事故造成260余人受伤。因此,研究地铁ATS 系统的风险控制机理,对于降低系统事故发生概率、保证列车系统安全运行具有重要意义。目前有关ATS 系统的研究集中在ATS 系统相关技术或设备的分析、设计、开发与优化,如:龙凡[2]提出了一种地铁车辆基地综合自动化系统与ATS 的接口设计方案;刘明霞[3]研究了ATS 系统与综合监控系统的集成方案;张澜[4]设计了一种ATS 系统仿真平台,对有效提升工程实施人员、运营操作人员以及设备维护人员的专业技术水平起到重大作用;高明生[5]分析和设计了ATS 系统中的扣车机制。部分文献涉及ATS 系统故障分析及可靠性研究,如:邝永松[6]分析了城市轨道交通ATS 系统故障对行车组织的影响,研究了降级行车组织方法以及优化ATS 故障降级行车组织模式;孙苑[7]利用动态故障树对地铁ATS 系统进行可靠性分析;贺鹏[8]为提高城市轨道交通列车运行自动监控系统ATS 的可靠性,提出了一种基于开放复杂大系统理论的城市轨道交通ATS 系统可靠性分析方法。总结上述研究可发现,深入挖掘地铁ATS 系统风险控制机理方面的成果较少。

目前关于系统风险控制的研究主要集中在两个方面:(1)基于风险评估或评价结果提出系统风险控制及管理措施。如:黄文成[9-11]认为危险品运输系统风险形成是基于各风险因素间的耦合作用,应尽量避免多因素耦合作用,降低耦合强度,从而控制风险;蒋翠清[12]提出基于样本和特征双重差异的协同训练模型TRICMV 进行P2P 网络借贷违约风险评价;颜波[13]将物联网环境下的农产品供应链风险因素总结为感知层风险、网络层风险、应用层风险以及其他风险,并使用OWA 算子对风险因素进行定量评估与排序,接着依据风险评估的结果使用供应链风险扩散收敛模型找出衡量供应链风险波动的定量指标,最后提出了物联网环境下农产品供应链风险管理与控制的措施和建议;王建新[14]依据商业银行信用风险的内涵,结合信用风险的不确定性和相对性特征,提出以“信用风险度”作为系统的输出,并针对传统模式识别评估方法的不足,构建了基于补偿模糊神经网络的信用风险评估预测模型,为有效转变信用风险的分类评估模式、提供更为全面的信贷决策支持奠定了基础。(2)通过研究系统风险的形成机理提出对应的风险控制或预警方法。如:黄文成[15]采用N-K 模型研究了铁路危险品运输系统耦合风险的形成机理,认为系统风险耦合值低于阈值时,风险可得到控制。还指出铁路危险品运输管理部门应该从管控人和管等关键因素、尽可能避免多因素耦合作用、尽可能避免在铁路危险品运输系统脆弱处发生耦合作用等方面入手,提高铁路危险品运输系统安全性;王阳鹏[16]基于突变理论建立了ATS 系统的安全状态预警模型,指出对于系统的安全状态而言,存在着由设备运行状态和人员操作状态两个控制变量所共同决定的临界线,系统状态一旦越过临界线,系统状态就会出现突变,事故就有可能发生,因此需要控制设备与人两个变量来避免系统状态越过临界线;胡振华[17]认为研发型联盟对风险的识别和预警直接决定了研发活动的成败,因此其对研发型联盟风险预警机制进行研究,以期帮助联盟决策者制定风险防范策略;杨扬[18]建立企业集团内部异质成员企业的微观行为模型,并通过多智能体仿真得到企业集团规模、外部市场状况以及子公司主导行为对企业集团信用风险延迟效应与溢出效应的影响;陆静[19]采用贝叶斯网络,研究了商业银行操作风险预警机制。部分文献涉及风险机理层面的内容,如:王阳鹏[20]应用尖点突变模型描述了铁路系统安全动态变化过程,论述了铁路系统安全中系统风险的概念,但未在微观层面给出系统风险存在的根本原因,以及风险控制的微观机理过程。

杜芬方程是描述共振现象、调和振动、次调和振动、拟周期振动、概周期振动、奇异吸引子和混沌现象的一种数学模型。工程领域中常被应用于信号检测,如:李兆昕[21]以杜芬方程为基础,探究了一种基于几何特征极半径不变矩的未知频率信号检测方法;田晓旭[22]使用杜芬方程及杜芬混沌算法对淹没在强噪声下的微弱正弦信号进行检测,采用四阶龙格库塔法求解杜芬方程,构建了一种可实现微弱信号检测的系统平台;芮国胜[23]提出了一种待测信号预处理与杜芬振子结合的弱信号检测算法,进一步提高杜芬振子检测的性能。根据以上分析可知,杜芬方程常用于信号检测而极少应用于风险控制机理研究。

地铁ATS 系统中既存在周期性风险也存在着非周期性风险,二者有明显区别,对系统影响效果也不同。篇幅限制,本文主要分析地铁ATS 系统的周期性风险控制机理。笔者将从系统微观角度出发,以地铁ATS 系统中的周期性风险为主要研究对象,采用杜芬方程刻画地铁ATS 系统的震荡与周期性风险,得出地铁ATS 系统的震荡方程,再由地铁ATS 系统的震荡方程推导周期性风险控制方程,通过周期性风险控制方程仿真得出系统震荡产生风险突跳的原因以及系统风险控制的机理。

1 地铁ATS 系统风险特性分析

Zeeman[24]指出,如果一个变化过程满足双模态、突变、滞后、不可达和分歧五个特征中至少两个特征时,则表明该变化过程可用突变理论描述。接下来将阐释地铁ATS 系统安全状态变化过程具有这五种特征。

(1)不可达:当地铁ATS 系统开始运行之后,系统安全状态会受到来自系统外部干扰和来自系统内部变化的影响,如人员操作失误或安全意识缺失、设备故障以及恶劣环境因素等[25],系统安全状态会随之发生变化。即当地铁ATS 系统开始运转后,系统的初始状态几乎无法维持,表明地铁ATS 系统安全的初始状态不可达。

(2)突变:某故障的发生可能会导致ATS 系统从安全状态突然变为危险状态,故障发生后采取的紧急措施可使列车系统状态从危险状态回到安全状态。因此在系统状态变化的过程中,这种在安全状态与危险状态之间的转换,可理解为突变。

(3)滞后:在地铁运营的高峰时期,地铁发车时间间隔小,发车频率较高,为检测每一辆列车情况,地铁ATS 系统一直处于高速运转状态。若此时高速运转的地铁ATS 系统发生了某种突发事件(人员失误操作或者工作间组件故障),导致其对列车的监控和控制能力下降,容易导致事故发生,此时ATS 系统进入了高风险状态。而在地铁运营低峰期,列车发车频率较低,地铁ATS 系统运转速度较慢,系统负荷低,此时突发事件对其影响较高峰时期更低。如图1 所示,A1-A4分别代表地铁ATS 系统低速运转、地铁ATS 系统高速运转、地铁ATS 系统高风险和地铁ATS 系统低风险。当系统处于A2 时突发事件发生,假设突发事件为某段通信线路故障,此时地铁ATS 系统需要接入备用线路并且通知维修人员前往维修。在线路故障到接入备用线路这段时间里,地铁ATS 系统暂时无法行使正常功能,此时系统状态由A2 转入A3 状态。当备用线路被接入后,ATS 系统正常运转,此时地铁ATS 系统风险下降,系统由A3 状态转入A4 状态。经过维修人员的维修后,线路故障完全排除,系统恢复正常。但系统完全恢复需要先进入低速运转,再进入高速运转,即系统由A4 状态先转入A1 状态再转入A2 状态。上述整个过程不可逆,两个不相邻的状态间不可跨越,即A2 不可直接转入A4,需要经过A3 才可转入A4,这种现象体现了地铁ATS 系统安全状态的滞后性。

图1 地铁ATS 系统运行状态变化过程Figure 1 The changing process of the changing state of the Metro ATS system

(4)双模态:若没有外部干扰与内部变化影响,地铁ATS系统将保持初始阶段的安全状态;若系统防护程度很高,地铁ATS 系统将始终处于安全状态;当系统风险很高时,地铁ATS 系统将处于风险状态。一般情况下,系统状态将在安全状态和风险状态之间转换,这便是地铁ATS 系统状态的双模态性。

(5)分歧:ATS 系统结构非常复杂,任一关键软件或硬件出现问题都可能导致事故。即使ATS 系统初始状态中存在一个很小扰动,最终都可能导致列车安全状态出现很大偏差,这一现象称之为地铁ATS 系统安全状态连续变化过程中的分歧。

综上,双模态、突变、滞后、不可达和分歧五种特性在地铁ATS 系统的风险状态变化过程中表现明显,所以利用突变理论描述地铁ATS 系统风险状态变化过程是可行的。

2 地铁ATS 系统的周期性风险和非周期性风险

地铁ATS 系统的风险是系统本身受到来自内部和外部的干扰引起的。有的干扰是重复的、周期性的,这一类干扰形成的风险称为周期性风险;有的干扰具有偶然性、突然性,将这一类干扰形成的风险称为非周期性风险。具体分类如下:

2.1 周期性干扰风险

(1)操作人员人为简化操作:地铁ATS 系统通常需要配备一定量的工作人员完成启动、关闭及调试等工作。部分工作人员为了节省时间,主观地简化某些必要的操作环节,并且在之后每一次操作中都简化相同的操作。这些简化操作通常比较细微,给系统带来的干扰较小,但当这些不合理操作带来的干扰积累到一定程度后,就可能造成地铁ATS 系统安全事故。

(2)操作人员错误理解操作规范:地铁ATS 系统操作员在阅读相关操作规范以及接受相关操作培训时,错误理解了某一或一些操作步骤,导致在今后的操作中重复错误操作,此类干扰具有周期性。

(3)来自其他信号系统的干扰:整个地铁运营系统中除了地铁ATS 系统外还有其他信号系统,均利用与列车之间的信号传递来保证列车的安全运行。当其他信号系统中设备故障以及人员操作失误等情况发生后,其发出的错误信号可能干扰到地铁ATS 系统的信号。通常,其他信号系统发出的信号是周期性的,因此此类干扰也属于周期性干扰。

(4)管理者主观简化管理步骤或对管理规范条例理解不到位:为节省时间成本,部分管理者主观简化了“不重要”的管理步骤,或部分管理者对管理条例理解不到位而导致错误操作。与(1)中所述人员操作类似,通常短时间内不会对系统造成巨大影响。在未发生事故前,此类管理者通常都会持续地错误操作,因此此类干扰也具有周期性。

2.2 非周期干扰风险

(1)所有环境变化以及自然灾害:地铁ATS 系统安全运行通常会受到来自外界环境的干扰,如:暴雨、洪水、地震等。自然灾害通常具有突然性、偶然性,因此这类干扰属于非周期性干扰。

(2)操作人员偶然误操作:经过长时间高度集中的工作后,工作人员难免在某些时刻出现疲劳等症状,导致错误操作,因此此类操作不具有周期性。

(3)设备故障:地铁ATS 系统设备故障的主要原因有:人员暴力操作机器、外界环境影响(如:雨水渗入机器、地震使得机器倒塌)、长期使用导致零件损耗严重。此类干扰是偶然发生或长期积累导致的,不具有周期性。

(4)管理时的疏忽:管理人员在管理时的疏忽导致事故发生,此类干扰不具有周期性。

地铁ATS 系统是一个时刻发生震荡的动态系统,若系统的震荡行为未出现突跳现象[15],则系统状态是稳定的,引发事故的概率较低;若系统震荡行为出现了突跳现象,系统状态是不稳定的,此时引发事故的概率较高。周期性风险与非周期性风险都是引发系统出现不稳定震荡的原因,篇幅所限,本文主要分析地铁ATS 系统周期性干扰带来的风险以及相应的控制机理,重点关注如何控制系统震荡行为中的突跳现象。

3 模型可行性分析

杜芬方程具有较多种类。本文采用硬特性杜芬方程[26]来描述地铁ATS 系统的震荡状态,建立地铁ATS 系统的震荡方程:

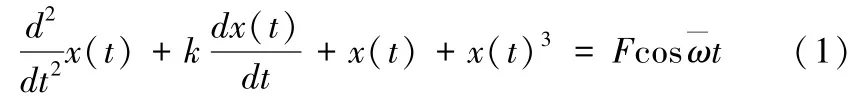
式中,x表示地铁ATS 系统的当前风险状态,其随时间变化而变化;t为地铁ATS 系统当前的运行时刻;k表示地铁ATS系统自身抵御风险干扰的能力,本文使用地铁ATS 组件概率重要度之和对其定量赋值[27];F表示地铁ATS 系统受到周期性干扰强度的峰值[28];为此周期性干扰强度变化的频率,由式(1)右端可知,杜芬方程所描述的干扰带有周期性的特点,即杜芬方程更加适合分析地铁ATS 系统的周期性干扰。综上,可以使用杜芬方程描述地铁ATS 系统状态的理论依据主要有三点:二者都是振动系统;二者都是非线性系统;二者的状态变化都可用尖点突变模型来描述。

(i)从振动理论的角度来看,杜芬方程描述的是典型的非线性振动系统,引起系统发生振动的本质是方程式(1)右端的余弦函数而地铁ATS 系统所受到的周期性干扰也会使系统的安全状态发生振动。从而引起周期性风险。

(ii)从非线性系统理论的角度来看,当系统的输出与输入不成正比关系时,可将这个系统称为非线性系统。杜芬方程由于含有立方项ax(t)3,其描述的一定是非线性系统。对于地铁ATS 系统而言,系统内部存在复杂的、非线性的信号转化和传递过程,其输入与输出信号不成正比例关系,因此地铁ATS 系统也属于非线性系统。

(iii)突变理论[29]研究的是系统状态从一种稳定状态跃迁到另一种稳定状态的非连续变化现象。一个系统所处的状态可用一组参数描述,当系统处于稳定状态时,标志该系统状态的势函数(如系统振动的振幅)取到唯一的极值。而当参数在某个范围内变化且该函数有不止一个极值时,系统将处于不稳定状态。目前最常见的突变模型是尖点突变模型,其势函数如下:

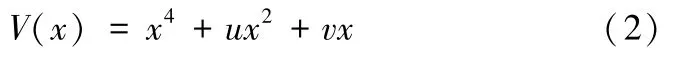
式中u,v为系统控制变量,x为系统状态变量。由第1 节地铁ATS 系统风险特性分析可知地铁ATS 系统风险状态变化可用尖点突变模型描述。由文献[30]可知杜芬方程也包含尖点突变模型,以某一含立方项的强迫Duffing 振动方程为例,假设为小量,则:

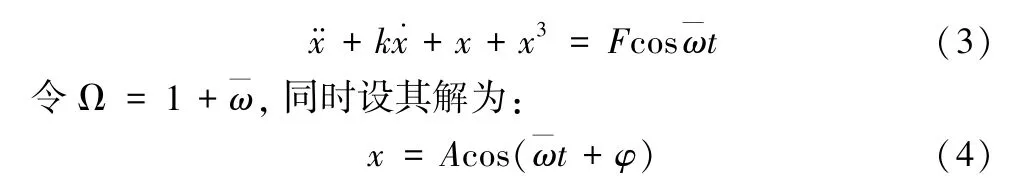
将(4)代入(3),令等号左右的一次谐波项系数相等并忽略三次谐波项得到:

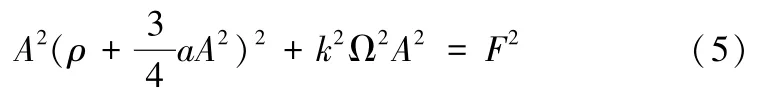
其中ρ=1 -Ω2,进行如下代换:

可得到由两个正则尖点突变组合而成的双尖点突变如下:

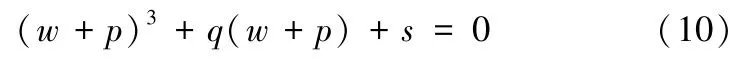
为求得尖点对应的位置,则需令:

依据式(12)可找到杜芬方程中尖点的位置,因此杜芬方程中存在尖点突变这一现象。基于上述分析,杜芬方程和地铁ATS 系统二者都随时间发生振动,都是非线性系统且都可用尖点突变模型来描述,因此可使用杜芬方程来建立系统的震荡方程,并基于震荡方程推导系统风险控制方程。

4 基于反馈控制法的系统周期性风险控制方程

地铁ATS 系统状态发生突跳将极易导致事故的发生,如何控制系统状态不发生突跳是研究风险控制的关键[15]。首先建立地铁ATS 系统中无调节反馈控制函数时的系统震荡方程,并基于此方程推导得到无调节反馈控制函数的地铁ATS 系统分岔响应方程;在无调节反馈控制函数的系统震荡方程基础上,分别向其中加入阻尼调节反馈控制函数和幅值调节反馈控制函数,并分别推导含阻尼调节反馈控制函数与含幅值调节反馈控制函数的地铁ATS 系统的周期性风险控制方程。

加入两种调节反馈控制函数的目的在于对地铁ATS 系统震荡方程中的系数进行调节(例如:阻尼调节反馈控制函数旨在调节(1)式中的系数k;幅值调节反馈控制函数旨在调节(1)式中的系数F)。对无调节反馈控制函数的地铁ATS 系统分岔响应方程进行仿真,可直接观测在受到周期性干扰后,地铁ATS 系统状态的突跳行为;而对含阻尼调节反馈和幅值调节反馈的周期性风险控制方程进行仿真,则可观测到地铁ATS 系统状态突跳行为被抑制的过程,从而获得地铁ATS 系统周期性风险的控制机理。最后同时向无反馈控制函数系统震荡方程之中加入阻尼、幅值这两种调节反馈控制函数,并推导相应的风险控制方程,并以此探究两种控制函数的具体关系。

4.1 无调节反馈控制函数的地铁ATS 系统分岔响应方程

对无调节反馈控制函数的地铁ATS 系统震荡方程(如(13)式所示)进行推导可得到相应的系统分岔响应方程,推导过程如下:

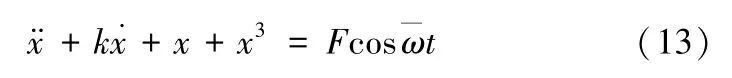
式(13)含有时间t,是非自治系统。为便于分析,使用多尺度法[31](之后的三个推导也使用了多尺度法)将其转化为不含时间变量t的自治系统。为此引入小参数ε,则(13)可表示为:

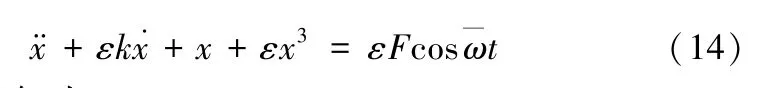
设(14)的近似解为:

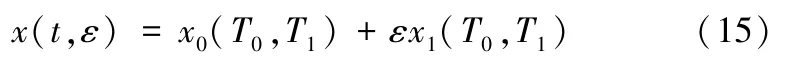
其中T0=t和T1=εt为独立的时间变量,分别代表一个较快变化的时间尺度和较慢变化的时间尺度。记D0=∂/∂T0,D1=∂/∂T1,则时间变量的导算子变为:

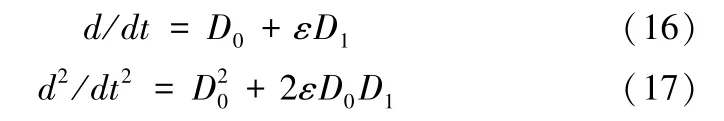
考虑主共振:

将(15)-(18)带入(14)中得:

展开后得:

比较上式ε的同次幂,有:

ε0阶:

ε1阶:

由(21)易得:

设上式(22)的解为:

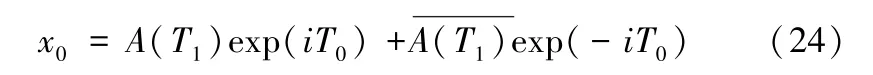
将(23)与(24)带入(22)中得:

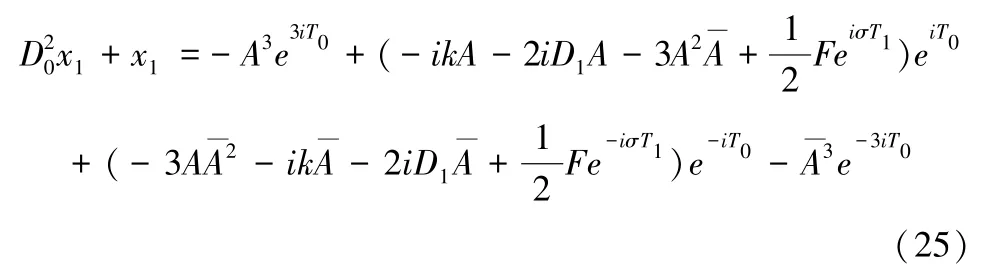
想上方程有周期解,则需要令:

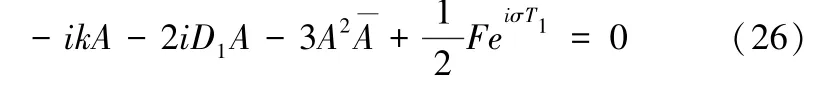
再设A的表达式为(其中r,θ为T1的实函数):

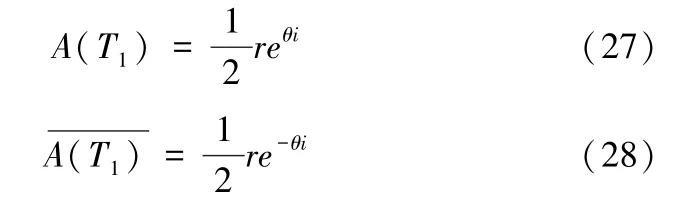
将(27)和(28)带入(26),再由欧拉公式eiθ=cosθ +isinθ可得:

分离实部与虚部得到平均方程:

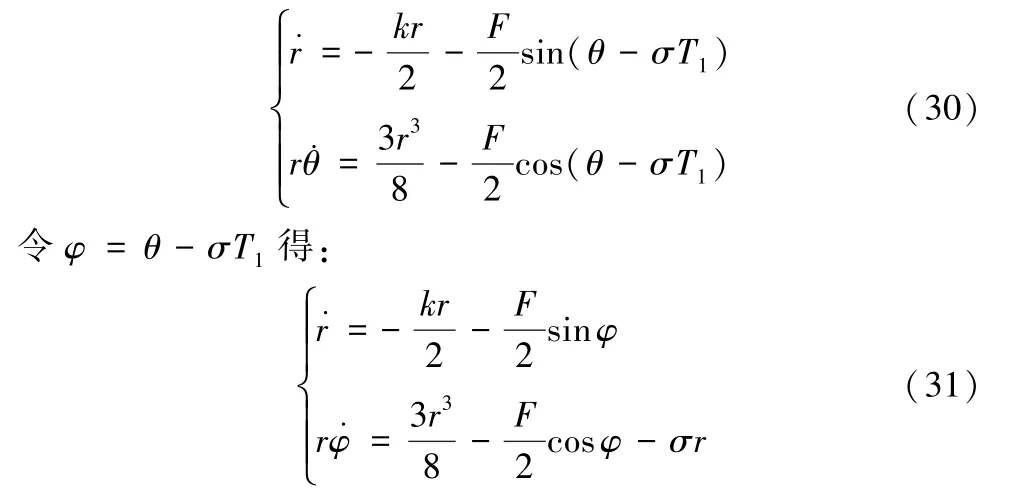
令等式右边等于0 得:

合并化简后得稳态解的分岔响应方程为:

式(33)即为地铁ATS 系统的分岔响应方程。该方程是一个关于σ和r的隐式方程,其中变量σ为周期激励频率与振子固有频率的接近程度,表示地铁ATS 系统受到的周期性干扰频率与地铁ATS 系统本身震荡频率的接近程度;变量r为震荡幅值,表示地铁ATS 系统震荡的幅值;k,F与第3 节中解释一致。若以σ为自变量,r为因变量对式(33) 进行数值仿真,便可得到系统在没有任何控制措施下的系统震荡情况,当某一σ的取值对应多个r取值时,则意味着系统中发生了状态突跳[15],此时系统中将会出现较大的风险波动,系统变得不稳定。

4.2 含阻尼调节反馈控制函数的地铁ATS 系统周期性风险控制方程

加强地铁ATS 系统的阻尼,从而加强ATS 系统自身抵抗干扰的防御力是有效控制系统周期性风险的方法之一。在式(14)中加入阻尼调节反馈控制函数u=得到(34)式,推导(34)式从而得到相应的周期性风险控制方程。

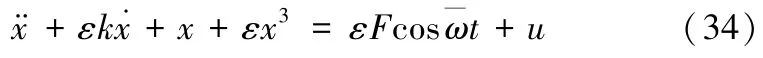
方程化为:

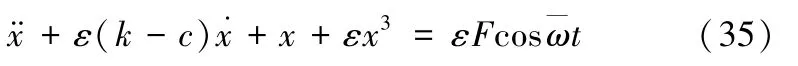
之后的推导过程与4.1 节推导过程相同,此处不再赘述,直接给出含阻尼反馈控制函数的周期性风险控制方程:

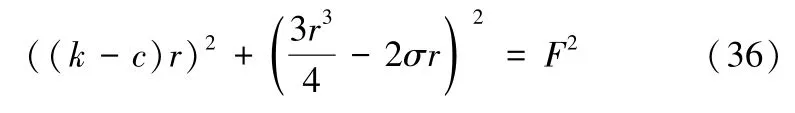
与(33)式相比,式(36)中k,σ,r,F各自对应的意义与4.1 节中解释一致,在阻尼系数k中加入了一个控制参数c,c在地铁ATS 系统中对应的意义是某种影响地铁ATS 系统阻尼的行为,阻尼系数因此变为k -c。在以σ为自变量、r为因变量对式(36)进行仿真时,可得到地铁ATS 系统在阻尼参数受到控制情况下的系统震荡情况。调节c的大小,当任一σ取值均对应单一r取值时,表示此时系统状态突跳已被抑制,系统的周期性风险得到了控制。

4.3 含幅值调节反馈控制函数的地铁ATS 系统风险控制方程

尽可能地降低外界环境对系统的干扰是又一有效的系统周期性风险控制方法,在式(14)中加入幅值反馈控制函数u=得到(37)式,推导(37)式从而得到相应的周期性风险控制方程。

方程化为:

之后的推导过程与4.1 节推导过程原理方法均相同,此处不再赘述,直接给出最后推导结果,即含幅值反馈控制函数的周期性风险控制方程为:

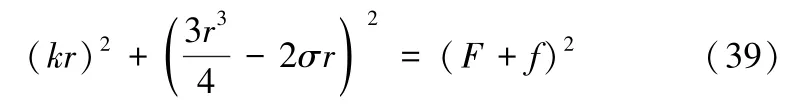
与式(33)相比,式(39)中k,σ,r,F各自对应的意义保持不变,与4.1节中解释一致,在外激励系数中加入了一个控制参数f,f在地铁ATS 系统中对应某种影响ATS 系统受到周期性干扰强度的行为,外激励参数因此变为F+f,此时以σ为自变量,r为因变量对式(39) 进行仿真,便得到了外激励系数受到控制情况下系统的震荡情况,调节f的大小,当σ取任一值对应r的取值始终只有一个时,此时系统的突跳行为已经得到了控制。

4.4 含阻尼调节与幅值调节反馈控制函数的地铁ATS 系统风险控制方程

为了探究阻尼调节与幅值调节反馈控制函数在抑制系统突跳、控制系统风险方面的作用关系,在(14)中同时加入阻尼调节反馈控制函数u1=与幅值调节反馈控制函数u2=得到(40)式,推导(40)式从而得到相应的周期性风险控制方程。

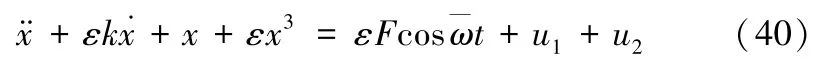
方程化为:

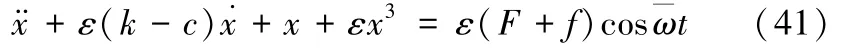
之后的推导过程与4.1 节推导过程原理方法相同,不再赘述,直接给出最后推导结果,即同时包含阻尼反馈控制函数与幅值反馈控制函数的周期性风险控制方程为:

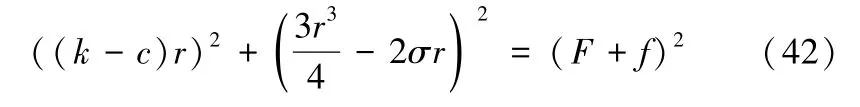
与式(33)、(36)、(39)相比,式(42)中k,σ,r,F各自对应的意义与4.1 节中解释一致,系数c与4.2 节相应解释一致,系数f与4.3 节相应解释一致。将式(42) 固定c,不固定f进行仿真得出系统突跳消失的临界取值f1,并与(39) 式仿真得出临界取值f2进行对比,可以得出阻尼反馈控制对幅值反馈控制的影响情况。同理,将式(42) 固定f,不固定c进行仿真得出系统突跳消失的临界取值c1,并与(36)式仿真得出临界取值c2进行对比,可以得出幅值反馈控制对阻尼反馈控制的影响情况。

5 案例分析

以北京地铁二号线ATS 系统为例进行案例仿真研究。基于地铁ATS 系统的设备数据确定出4 个周期性风险控制方程(如(33)(36)(39)(42)所示)中系数k、F、c、f的取值,再对以上4 个周期性风险控制方程进行仿真,最后将仿真结果进行对比得出结论。

5.1 控制方程参数设定

利用北京地铁二号线ATS 系统的主要部件故障率和故障树确定k,F的取值,在仿真时需要不断调整控制参数c,f的取值,故而设定多个c,f的取值。

(1)k的取值

k为系统阻尼度,文中代表地铁ATS 系统自身抵抗外部干扰的能力。在地铁ATS 系统中某个组件的概率重要度[27]代表其与整个系统之间联系的紧密程度,该组件概率重要度越大,表明其与整个地铁ATS 系统联系越紧密。由于地铁ATS 系统的内部组件与ATS 系统联系的紧密程度决定了地铁ATS 系统自身抵抗干扰的能力,因此本文使用地铁ATS 系统所有组件概率重要度之和来表示地铁ATS 系统整体抵抗干扰的能力,即将k的取值定为地铁ATS 系统组件概率重要度之和。下面将以北京地铁二号线ATS 为例,计算其组件概率重要度之和。首先构建如图2 所示的北京地铁二号线ATS 系统设备故障树,再根据表1 中的北京地铁二号线ATS 系统主要部件的故障率,计算可得地铁ATS 系统组件的概率重要度。

表1 北京地铁二号线ATS 系统主要部件的故障率[7]Table 1 The failure rate of the main components of the ATS system in Beijing Metro Line 2[7]

图2 北京地铁二号线ATS 系统设备故障树[16]Figure 2 The fault tree of the equipment of the ATS system in Beijing Metro Line 2[16]

对表1 中的数据和图2 所示的故障树进行分析与计算可得出,北京地铁二号线ATS 系统中各组件的概率重要度如下表2 所示。对表2 中所有组件概率重要度求和,即可得k的取值为0.2045。

表2 北京地铁二号线ATS 系统中各组件的概率重要度[16]Table 2 The probability importance of the components in the ATS system of Beijing Metro Line 2[16]

(2)F的取值

F为北京地铁二号线ATS 系统受到周期性干扰强度的峰值,其取值范围为[0,1](F取0 表示无周期性干扰,F取1表示周期性干扰所能达到的峰值已经达到最大值)[28]。由于F的取值主要受各种周期性干扰强度影响,因此不同时间点周期性干扰所能达到的最大值是不同的,故F的取值无法找到明确的初始取值,本文设其初始取值为0.45。

(3)c的取值

c为阻尼调节反馈控制参数,用来调节k的大小。为了在仿真结果中体现调节参数k变化给地铁ATS 系统状态带来的变化,c取多个不同的值,本文取c=0,c=-0.1,c=-0.33,c=-0.4。

(4)f的取值

f为幅值调节反馈控制参数,用来调节F的大小。为了在仿真结果中体现调节参数F变化给地铁ATS 系统状态带来的变化,f取多个不同的值,本文取f=0,f=-0.22,f=-0.35,f=-0.4。

5.2 周期性风险控制方程的仿真

(1)无反馈控制函数的地铁ATS 系统风险分岔响应方程仿真以及k的敏感度分析

将k=0.2045,F=0.45 代入无反馈控制函数的地铁ATS 系统分岔响应方程(即式(33))进行仿真,仿真结果如图3 所示。图3 中,横坐标σ为协调参数,表示北京地铁二号线ATS 系统受到的周期性干扰频率与系统自身波动频率的接近程度。纵坐标r为北京地铁二号线ATS 系统震荡的幅值。分析图3 可知:(1)当σ ＜σ1时,r随着σ的增大而增大,且此区间内两者一一对应,当σ确定时,振幅r同时确定。因此地铁ATS 系统在此区间内的震荡状态能够取到唯一极值,地铁ATS 系统处于稳定的状态;(2)当σ1≤σ≤σ2(σ1=0.48026,σ2=1.62335)时,σ取单一值时所对应的r取值不唯一(其中当σ=σ1或σ=σ2时一个σ对应两个r,当σ1＜σ ＜σ2一个σ对应三个r),即此区间内的任一σ处,系统的震荡状态无法取到唯一极值,此时地铁ATS 系统震荡的振幅r会发生突跳(即系统震荡的振幅在多个振幅取值中来回变化),系统进入不稳定的状态;(3)当σ ＞σ2时,σ与r恢复一一对应,地铁ATS 系统又恢复到了稳定状态。

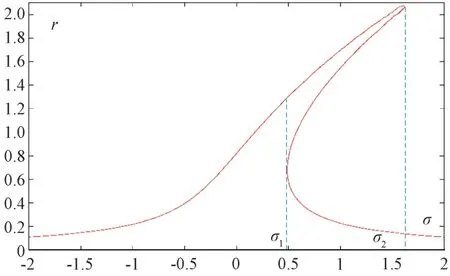
图3 无反馈控制函数的地铁ATS 系统分岔响应方程仿真结果Figure 3 The Simulation of the bifurcation response equation of the Metro ATS system without feedback control functions

为探究k的敏感度,在[0.2045,0.3045]区间内依次取多个值赋予k,并一一带入式(33)中进行仿真,仿真结果如图4 所示。由图4 可知,随着k值得不断增加,系统发生突跳的区间,即系统的不稳定区间[σ1,σ2] 不断缩小,系统发生事故的概率不断降低。因此,随着系统组件概率重要度之和不断增加,系统阻尼度不断增加,系统的风险不断降低。若系统初始便拥有较高的k取值,即较高的组件概率重要度之和,则系统的初始风险较低。

图4 不同k 取值情况下无反馈控制函数地铁ATS 系统分岔响应方程仿真结果Figure 4 The Simulation of the bifurcation response equation of the Metro ATS system without feedback control functions under the different k values

(2)含阻尼调节反馈控制函数的地铁ATS 系统周期性风险控制方程仿真

将k=0.2045,F=0.45 代入含阻尼调节反馈控制函数的地铁ATS 系统周期性风险控制方程(即式(36))并分别对c取c=0、c=-0.1、c=-0.33、c=-0.4 进行仿真,仿真结果如图5 所示。首先对比图3 可知,红线所示(c=0)是无反馈控制函数的地铁ATS 系统风险分岔响应方程仿真结果。随着c的不断减小,北京地铁二号线ATS 系统的整体阻尼系数k -c不断增加,系统自身的防御属性加强,一个σ对应多个r的区间不断缩小,地铁ATS 系统震荡状态不稳定的区间不断缩小,即地铁ATS 系统在震荡过程中发生突跳的可能性不断减小,ATS 系统发生事故的概率不断下降。当c=-0.33 时,由绿色曲线可知,不论σ如何变化,σ与r始终保持一一对应,地铁ATS 系统震荡状态可以取到唯一极值。由此可以得到结论,当c≤- 0.33,即系统阻尼系数k -c≥0.5345 时,地铁ATS 系统震荡的突跳行为消失,系统将始终处于稳定状态。通过上述分析可知,通过选择合理的阻尼控制参数能够控制地铁ATS 系统受到的周期性风险,使系统安全状态趋于稳定。

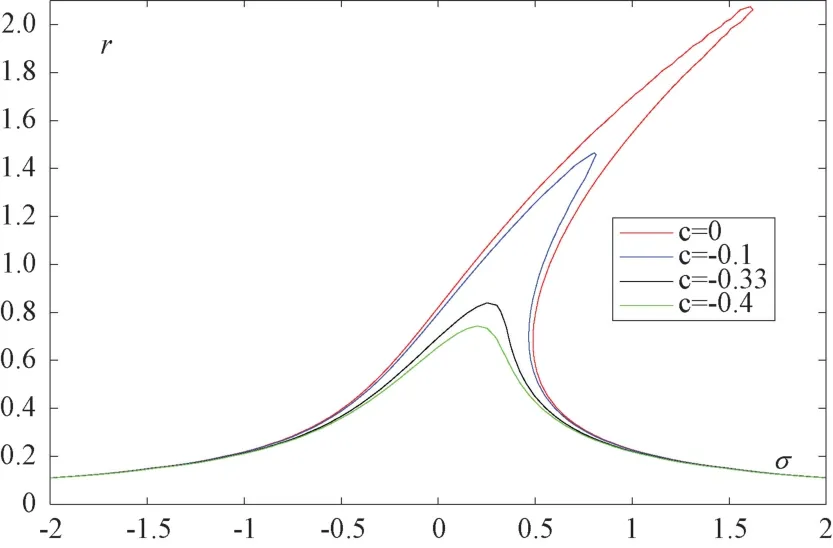
图5 含阻尼调节反馈控制函数的地铁ATS 系统周期性风险控制方程仿真结果Figure 5 The simulation of the periodic risk control equation of the Metro ATS system with the damping feedback control function

(3)含幅值调节反馈控制函数的地铁ATS 系统周期性风险控制方程仿真

将k=0.2045,F=0.45 代入含幅值调节反馈控制函数的地铁ATS 系统周期性风险控制方程(即式(39))并分别对f取f=0、f=-0.22、f=-0.35、f=-0.4 进行仿真,仿真结果如图6 所示。由图6 可知,红线所示(f=0)为无反馈控制函数的地铁ATS 系统风险分岔响应方程仿真结果。随着f的不断减小,北京地铁二号线ATS 系统的整体外激励系数F+f不断减小,地铁ATS 系统受到的周期性干扰被减弱,振幅r无法取到唯一值的区间不断缩小,地铁ATS 系统震荡状态不稳定的区间不断缩小,地铁ATS 系统震荡发生突跳的可能性不断降低。当f=-0.35 时,由绿色曲线可知,不论σ取何值,σ与r始终一一对应,地铁ATS 系统震荡状态可取到唯一极值,地铁ATS 系统处于稳定状态。由此可得到结论,当f≤- 0.35 时,即系统外激励系数F+f≤0.1 时,北京地铁二号线ATS 系统震荡的突跳行为彻底消失,该系统将一直保持在稳定状态,可通过选择合理的外激励控制参数控制地铁ATS 系统所受到的周期性风险,使系统安全状态趋于稳定。

图6 含幅值调节反馈控制函数的地铁ATS 系统周期性风险控制方程仿真结果Figure 6 The simulation of the periodic risk control equation of the Metro ATS system with the amplitude feedback control function

5.3 阻尼调节反馈控制与幅值反馈控制关系仿真研究

为了探究阻尼调节反馈控制与幅值反馈控制之间的关系,需要对式(42)进行仿真。首先固定f的取值,令f=-0.181,c分别取0、-0.1、-0.27、-0.33,仿真结果如图7(a)所示。其次,固定c的取值,令c=-0.1,f分别取0、-0.22、-0.29、-0.35,仿真结果如图7(b)所示。

由图7(a)可知,当c≤- 0.27 时,地铁ATS 系统震荡的突跳行为消失,系统将处于稳定状态,即系统突跳行为被抑制的临界值为c1=-0.27。将图7(a)与图5 对比并结合5.2 节(2)分析可知,当系统只含有阻尼调节反馈控制函数时,系统突跳行为被抑制的临界值为c2=-0.33,易得代表系统阻尼控制行为的控制强度),因此将幅值调节反馈控制函数加入含阻尼调节反馈控制函数的地铁ATS 系统周期性风险控制方程中可以使系统突跳行为被抑制的临界阻尼控制强度下降,即幅值调节反馈对阻尼调节反馈有促进作用。同理,由图7(b)可知,当f≤- 0.29,地铁ATS 系统震荡的突跳行为消失,系统将始终处于稳定状态,即系统突跳行为被抑制的临界值为f1=-0.29。将图7(b)与图6 对比并结合5.2 节(3)中分析可知,当系统只含有幅值调节反馈控制函数时,系统突跳行为被抑制的临界值为f2=-0.35,易得代表系统幅值控制行为的控制强度),因此将阻尼调节反馈控制函数加入含幅值调节反馈控制函数的地铁ATS 系统周期性风险控制方程中可以使系统突跳行为被抑制的临界幅值控制强度下降,即阻尼调节反馈对幅值调节反馈有促进作用。综上所述,阻尼调节反馈控制函数与幅值调节反馈控制函数,在控制系统突跳、降低系统周期性风险方面有相互促进的作用。

图7 含阻尼调节反馈与幅值调节反馈控制函数的地铁ATS 系统周期性风险控制方程仿真结果Figure 7 The simulation of the periodic risk control equation of the Metro ATS system with the damping feedback control function and the amplitude feedback control function

5.4 结果总结

由仿真结果可知:(1)若不向地铁ATS 系统震荡方程中加入任何反馈控制函数,即不对地铁ATS 系统施加任何控制措施,在σ取[0.48026,1.62335] 时,北京地铁二号线ATS系统震荡会出现突跳的情况,此时系统震荡极其不稳定,易发生事故,且由系统阻尼度k的敏感度分析可知,系统初始阻尼度越高,系统初始出现突跳的概率就越低;(2)向地铁ATS 系统震荡方程中加入的阻尼调节反馈控制函数,通过控制参数c在特定范围(c≤- 0.33) 内能够使系统阻尼系数增大,从而提升系统自身抵抗能力,系统震荡的突跳行为消失,并保持稳定状态,杜绝事故发生。在实际安全管理控制中,此类调节控制参数c从而增加系统自身防御力所对应的措施有:增加对系统设备的检修频率,完善和规范设备操作方法等;(3)向地铁ATS 系统震荡方程中加入的幅值调节反馈控制函数u=,通过控制降低f到一定范围(f≤- 0.35) 内,能够使得外激励系数下降,地铁ATS 系统受到的周期性干扰减弱,从而使系统震荡的突跳行为消失并保持稳定状态,避免事故发生。此类调节控制参数f从而降低地铁ATS 系统受到周期性干扰强度的控制措施如:在制作有关操作规范条例和有关管理规范条例时,对每一项步骤进行更加清晰明确地解释,避免操作人员或管理人员出现误解;对操作人员进行进一步监管,杜绝个别操作人员为了节省时间成本而私自简化操作;在不同信号系统之间,加强信号的互相屏蔽措施,防止不同系统间信号的互相干扰等。(4)在控制系统周期性风险方面,阻尼调节反馈控制与幅值调节反馈控制作用之间存在着相互促进的关系,因此在实施阻尼控制措施(或幅值控制措施)的同时,再实施一定的幅值控制措施(或阻尼控制措施)更加有利于控制系统的周期性风险。

总结地铁ATS 系统周期性风险控制机理如图8 所示。由图8 可知,宏观领域的地铁ATS 系统周期性风险控制通常由决策者提出一项风险控制措施继而将其应用于ATS 系统的安全管理控制中,最后地铁ATS 系统周期性风险得到控制。该宏观过程对应的微观机理为:(1)决策者每提出一项周期性风险控制措施都对应一个反馈控制函数;(2)将周期性风险控制措施应用于地铁ATS 系统,对应将反馈控制函数加入地铁ATS 系统的震荡方程中;(3)实行措施后系统周期性风险得到控制,对应加入反馈控制函数并对系数进行调节后地铁ATS 系统震荡过程中突跳行为的消失。

图8 地铁ATS 系统周期性风险控制机理Figure 8 The periodic risk control mechanism of the Metro ATS system

6 结束语

本文基于杜芬方程建立地铁ATS 系统周期性风险的反馈控制模型并用于研究风险控制机理,为我国地铁ATS 系统风险控制机理奠定了一定的理论基础。首先,本文分析了地铁ATS 系统的风险特性,同时明确地铁ATS 系统中所存在的周期性风险和非周期性风险,同时从振动、非线性以及突变三个方面阐明使用杜芬方程描述地铁ATS 系统状态变化以及周期性风险影响作用的可行性,然后将杜芬方程中所含参数与变量赋予描述地铁ATS 系统状态属性的实际意义,以此建立ATS 系统的震荡方程。最后,本文向地铁ATS 系统震荡方程中加入反馈控制函数以调节地铁ATS 系统震荡方程中的系数,采用多尺度法推导出加入不同形式的反馈控制函数时系统的分岔响应方程,即地铁ATS 系统的周期性风险控制方程。以北京地铁二号线ATS 系统为例对含不同反馈控制函数的地铁ATS 系统周期性风险控制方程进行仿真。仿真结果表明:使用反馈控制函数调节地铁ATS 系统震荡方程中的系数k,F,可以有效地削弱地铁ATS 系统震荡的突跳行为。而只要将系数对应的控制参数控制在某一阈值之下,便可以彻底控制地铁ATS 系统震荡的突跳问题,也就最大程度上的控制了地铁ATS 系统的周期性风险,使地铁ATS 系统完全处于稳定的状态。有关部门对于ATS 系统的防护措施应主要从两点入手:(1)加强ATS 系统内部主机设备的维护与保养,提高地铁ATS 系统自身防御能力;(2)进一步明确、细化各项操作和管理规范,降低ATS 系统设备受到周期性干扰的强度。在微观领域中这些宏观措施以反馈控制函数的形式作用于地铁ATS 系统震荡方程,当地铁ATS 系统震荡不发生突跳时,系统周期性风险便被控制。下一步将研究地铁ATS 系统的非周期风险控制机理。