基于深度强化学习的城市公共交通票价优化模型

李雪岩张汉坤李静邱荷婷

(1.北京联合大学 管理学院,北京 100101;2.北京工商大学 电商与物流学院,北京 100048;3.北京交通大学 经济管理学院,北京 100044;4.首都经济贸易大学 管理工程学院,北京 100070)

0 引言

票价制定是实现城市交通系统客流调控、疏解拥堵的重要手段。然而,目前我国大部分城市的公共交通系统运营都处于整体亏损状态。除去建设费用高昂、公益性等因素外,一个重要原因就在于网络化多模式公共交通系统条件下,多种影响出行需求的因素耦合联动,票价的调节机制相对滞后,难以在高额成本和群体出行需求的双重约束下实现经济效益与社会效益的有效权衡。可见,如何设计科学合理的票价调节机制,使其有效捕捉具有复杂性、异质性、机动性的出行需求,从而减少运营亏损、平衡运输资源配置值得高度关注并亟待解决。

国内外已有较多文献从不同角度对城市公共交通票价的制定问题展开了研究,就研究此类问题的总体思路而言,城市公共交通票价制定问题可以转化为由票价管理部门与出行者构成的、具有双层反馈结构的决策优化问题。上层决策目标包含利润或社会福利最大化、线路区间价格合理性、不同运输方式间的竞争均衡性、最优补贴策略等;下层决策则主要通过出行者对效用的感知过程刻画其选择行为。票价寻优的关键之一在于获取出行需求对票价的反应函数,目前的可行方法主要包括:通过变分不等式获取出行需求对价格变动的近似导数关系[1-2]、使用出发点到终点(origendestination,OD)间潜在需求与弹性系数构造弹性出行需求[3]、基于回顾性调查建立多变量模型分析票价变动对居民效用获得的影响[4]、试错迭代法[5]、均衡配流分析法[6]等。然而,在大多数既有的票价优化问题中,出行需求大多基于一般均衡理论被刻画为具有完全理性特征[6-7],可见,此类研究虽然获取了票价的严格长期均衡,但均对出行者的内在决策过程及行为复杂性进行了不同程度的简化,存在一定程度的反直觉悖论特征[8]。

显然,这种对出行者群体复杂决策过程的简化会带来价格决策有效性的偏差。大量研究都曾表明,交通系统内的决策行为不同于个人基于备选方案的单纯比较,个体行为之间并非相互独立的,在人们的出行决策过程中存在着广泛的社会互动效应[9-10],仅将个体行为进行简单的加总得到的宏观现象势必与现实情形存在差异。因此,研究者开始从社会学、行为科学角度,分析社会交互机制对交通行为的动机与特性的影响[11]。以占据公共交通系统客流较大比重的通勤客流为例,其内部就存在着强烈的社会互动以及典型的异质风险决策类型,如保守型与冒险型乘客的价格、时间敏感度差异、支付意愿差异、心理账户[12]等,这些因素均会促使群体决策结果发生均衡转移,继而使不同运输方式的分担率产生波动[13]。可见,由日常出行活动凝聚而成的出行群体形成了一个特殊的人际社会网络,随着具有异质特征的风险态度、行为模式、选择偏好在人际社会网络中的传播[14],传统研究中出行需求与票价之间的关系已经由简单的线性弹性关系转变为多维复杂的非线性反馈关系。

由上述文献可知,除去出行需求本身的动态变化以外,与出行需求演化机理相关的内生变量也是影响出行需求的重要因素,因此票价制定过程中需要参考的变量与因素将进一步复杂化。基于这一问题,本文将公共交通票价的制定与调节视为一个在复杂社会经济系统中经过不断探索与调节而实现价格优化的学习过程(符合实际生活中各种价格方案的实施过程)。深度Q 值强化学习(deep Q-learning,DQN)算法提出以来[15],以DQN 为典型代表的深度强化学习思想不断被应用于城市交通系统的智能化研究并已经在地铁客流诱导[16]、交通能源分配[17]研究中取得了良好的效果,其基本原理是在较为复杂的决策环境里,通过对智能体的输出动作进行评分和奖励,逐步训练其达到决策目标(图1)。深度强化学习方法的突出优点在于其采用了价值函数神经网络的方式感知复杂、高维的环境变化,并据此评价决策动作的输出;这一建模思想,是对传统的、基于一般均衡理论的票价优化方法的重要补充。

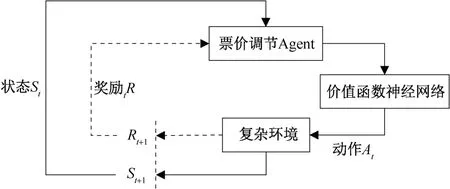
图1 深度强化学习的基本逻辑Figure 1 The basic logic procedure of deep reinforcement learning

在出行者群体决策复杂性条件下,出行需求与票价之间的关系转变为多维复杂的非线性反馈关系,因此,本文将具有较强非线性特征表现能力的价值函数神经网络用于拟合出行需求(环境)对票价调整(动作)的反应函数,实现出行需求不确定性条件下票价的动态调整,形成一套双层反馈结构下具有复杂需求感知能力的票价优化方法。

1 基于Deep Q Learning 的票价优化模型

1.1 模型基本假设

(1)出行方式票价决策。考虑两站点之间的出行活动,出行方式划分为:①目标出行方式;②其他出行方式;不同出行方式间存在竞争关系,本文将DQN 方法运用于目标出行方式i的票价优化(1.2 节与1.3 节);为了便于对比分析基于DQN 的票价调节策略与既有方法对出行需求的感知差异,其他出行方式的票价采用传统双层规划方法进行优化(详见1.4 节)。

(2)出行者群体决策复杂性。交通系统出行需求演化所产生的复杂性不仅是引入深度强化学习思想实现票价优化的原因,也是现实生活中广泛存在的实际现象。大量研究已表明,出行者群体决策的生成、演化过程受到有限理性与社会交互作用的共同影响,因此,本文将目前已被运用于出行行为复杂性研究的多主体建模、累积前景理论进行有机结合,刻画具有社会交互机制的群体出行选择决策。

出行者群体的基本假设如下:①出行者群体被划分为风险爱好与风险厌恶两种不同的风险态度类型,风险爱好者倾向于更少的出行费用预算,风险厌恶者倾向于更多的出行费用预算;②出行者对出行效用的判断由票价、行程时间、出行方式的舒适度构成;③出行者的风险态度会随时间变化并受到由人际网络构成的社会环境的影响,在不同的风险态度类型之间切换;模型构建详见第2 节。

1.2 票价调节强化学习模型构建

深度强化学习算法的原理是在复杂的环境状态下,通过对智能体输出动作的评分和奖励逐步训练其达到决策目标,本文借鉴深度强化学习算法中智能体对复杂环境的适应过程来设计票价调节策略与复杂出行需求之间的反应函数。

将t时刻OD对w间目标出行方式i的票价调节策略设置为模型的动作变量Δpi,t,Δpi,t的动作即为提价或降价的幅度,Δpi,t的决策空间做如下设置:Δpi,t∈{在pi,t的基础上降价Δpk%,……,在pi,t的基础上降价Δp2%,在pi,t的基础上降价Δp1%,票价不变,在pi,t的基础上提价Δp1%,在pi,t的基础上提价Δp2%,……,在pi,t的基础上提价Δpk%}(Δp1＜Δp2＜…＜Δpk);将票价调节后OD 间出行群体演化产生的不同出行方式的客流量qi,t(由出行群体交互模型得到,即出行需求)、不同出行方式的票价pi,t作为算法中的状态变量Sw,t;将目标出行方式i的运营收入作为奖励值R(Sw,t,Δpi,t),状态Sw,t条件下,对于票价调节策略Δpi,t,其评分值Q(Sw,t,Δpi,t) 的一般形式可由贝尔曼方程表示为:

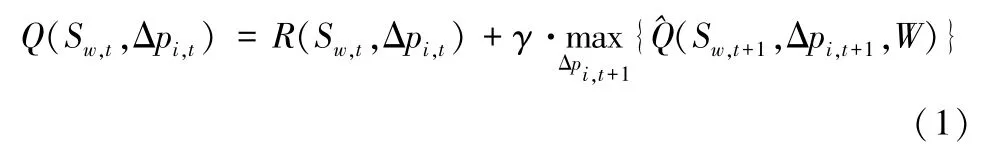
其中,γ表示强化学习参数,在复杂的出行需求演化条件下,问题的状态集合规模不断增大,票价的调节往往伴随着很大的状态空间和连续的动作空间,此时就需要用一个准确的价值函数来表示不同票价调节策略的评分值。遵循深度强化学习中所广泛采用的方法,本文引入具有较强非线性特征描述能力的神经网络来表征价格调节策略的价值函数,并基于loss 函数训练,其中,当票价落在合理区间内时,奖励值R(Sw,t,Δpi,t)由t时刻实施票价调节策略Δpi,t后出行方式i获得的利润构成:

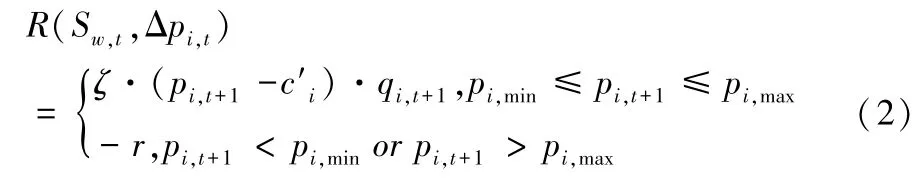
其中,ζ表示奖励系数,表示单位成本,当票价落在合理区间[pi,min,pi,max] 外时会产生惩罚-r,相比于硬性约束,“惩罚” 机制的设计有利于票价调节动作在“错误” 中积累经验,qi,t+1由票价作用下出行者群体的出行需求演化结果得到(详见第2 节)。

1.3 Deep Q Learning 票价优化策略训练方法

本文采用DQN 的思想训练票价调节的动作变量,DQN主要使用的技巧是经验回放,即将出行者群体与其他运输方式每次对票价的反应(状态变量)与相应的奖励值都保存起来,用于依据(1)式进行票价调节策略(动作变量)评分值Q(Sw,t,Δpi,t) 的更新,基于更新后的Q(Sw,t,Δpi,t),通过梯度的反向传播来更新神经网络的参数W,当W收敛后,即可得到票价调节策略价值函数的准确形式,通过票价调节策略(动作变量) 的不断迭代,得到最终的票价优化结果。

具体训练步骤如下:

步骤1初始化神经网络的参数,基于W初始化所有票价调节策略的评分值Q(Sw,t,Δpi,t),令票价调节经验回放集合为D。

步骤2构建状态特征向量Sw,t=[pi,t,qi,t,p-i,t,q-i,t],其中,-i表示其他运输方式,p-i,t表示其他运输方式的票价,q-i,t表示其他运输方式的出行需求,令Nw表示OD对w间的总体出行需求,则有qi,t +∑q-i,t=Nw。在神经网络中令Sw,t与Δpi,t作为输入,得到每一种票价调节策略对应的评分值输出,采用贪婪算法选择评分高的票价调节策略(以概率εt随机选择票价调节策略,以概率1-εt选取评分最高的票价调节策略,εt随时间递减Δε)。

步骤3在状态Sw,t执行当前动作,则pi,t+1=pi,t +,新的票价对其他运输方式及出行者群体决策产生影响后,得到新状态Sw,t+1=[pi,t+1,qi,t+1,p-i,t+1,q-i,t+1]及其奖励值R(Sw,t,Δpi,t),其中,其他运输方式的票价p-i,t+1由传统双层规划方法得到(详见2.4 节),q-i,t+1由实施票价调节策略后客流量的演化结果得到(详见2.2 节不同行为假设条件下的客流演化模型)。

步骤4将存入经验回放集合D,令Sw,t=Sw,t+1。

步骤5从经验回放集合D中随机选取若干状态样本,依据(1)～(2) 式更新评分值Q(Sw,t,Δpi,t)。

步骤6基于均方差函数,W)]2,通过梯度反向传播更新神经网络参数W。

步骤7完成一轮迭代,转到步骤2。

每次以状态变量及票价调节策略作为神经网络输入,均可得到针对每一种客流量状态的最优票价调节结果,因此,以任意客流量为初始状态,经过票价调节策略的多轮迭代,即可得到最终的票价优化结果。

1.4 基于DQN 方法的票价优化模型

对于目标出行方式以外的其他出行方式-i,其优化问题可以表示为双层规划模型:

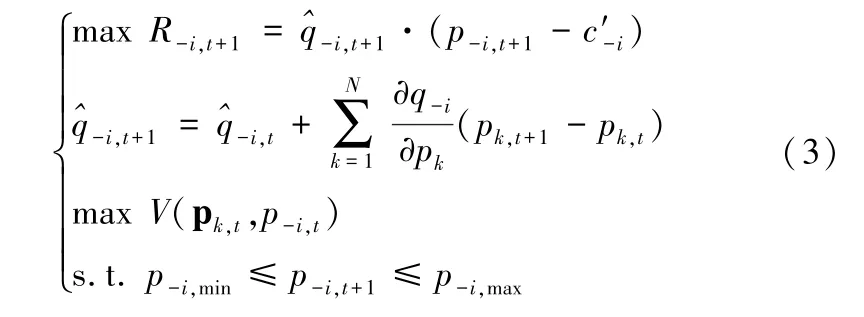
因此,对目标出行方式i引入基于DQN 的票价优化策略后,双层规划问题更新为:

由规划问题(4)可知,引入DQN 策略后,目标出行方式i票价变动的弹性通过DQN 中的价值函数神经网络获取,其他出行方式-i的票价则沿用传统优化方法获取。神经网络的使用,可以更加精细化地捕捉出行方式-i票价的变化及下层规划maxV(pi,t,p-i,t) 产生的出行需求复杂性。

2 基于有限理性社会交互机制的群体出行决策

2.1 出行效用

(1)出行者社会人际网络

现实中的出行者群体人际网络具有小世界特性,本文直接引入既有研究中的出行者小世界网络构造方法[19]建立规模为n × n的出行者群体二维空间网络结构,构建方法如下。

步骤1设置区域x∈[1,n],y∈[1,n] 为出行者群体产生的网格区域,每个网格节点代表一个出行者,则出行总需求为Nw=n2,每个出行者与上下左右四个出行者((x ±1,y),(x,y ±1)) 建立连接,形成规则网络。

步骤2遍历每一个出行者节点,依断点重连概率断开其与上下左右任意一个出行者之间的连接,然后与上下左右四个出行者以外的任意一个出行者建立连接,形成新的“邻居”关系。

图2 出行者社会人际网络Figure 2 Traveler's social network

文献[19]考察了上述网络构建方式得到的网络聚合系数与平均最短距离,研究表明,当断点重连概率为0.5 时,人际网络具有小世界特征。

(2)参照点

令Fi,t表示t时刻出行方式i的感知出行费用(负效用),服从正态分布,Fi,t～N[fi,t,(σi,t)2],其中:

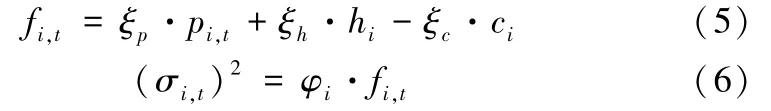
其中,hi与ci分别表示出行方式i的行程时间与舒适度,考虑不同出行方式的容量与拥挤因素,设置ci正比于交通载具的定员;ξp,ξh,ξc分别为相应惩罚系数,则ξc·ci表示出行费用的拥挤度惩罚项[20];φi表示出行方式i的变异系数,用来描述出行方式的稳定性。

进一步,令ρ(ρ∈(0,1)) 表示出行者群体的整体风险态度,依据既有研究中对出行者心理账户的刻画方式,对于出行者群体整体而言,出行方式i的费用预算可以表示为:

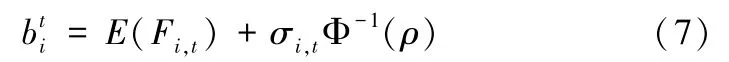
其中,Φ-1(·) 为正态分布函数的反函数,对于出行者的风险爱好与风险厌恶两种态度,其参照点可以表示为:

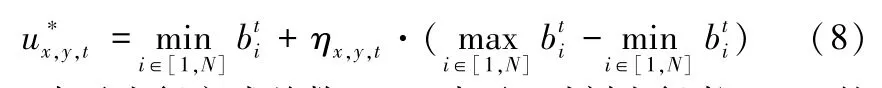
其中,N表示出行方式总数,ηx,y,t表示t时刻出行者(x,y) 的风险态度,,η1表示风险爱好,η2表示风险厌恶。

(3)累积前景效用

针对前景效用的刻画,本文继续沿用文献[21][22]的方法,在置信水平98%的置信区间内对Fi,t进行离散化,得到k个可能的费用结果及相应的概率,从而依据效用的离散分布模拟其连续分布。依据累积前景理论,t时刻出行者(x,y) 选择出行方式i的价值函数可以表示为:

其中,α与β表示出行者的风险偏好系数,λ表示损失规避程度。可见,当出行费用低于参照点时,出行者获得收益,反之出行者遭受损失;Fi,t离散化后,如的可能费用结果有b个,的可能费用结果有b'个,则收益与损失部分的累积决策权重可分别表示为:

其中,ω表示累积前景理论研究中常用的决策权重函数,则t时刻出行者(x,y) 选择出行方式i的累积前景出行效用可以表示为:

其离散形式为:

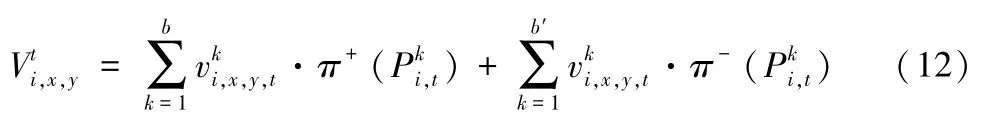
2.2 出行方式选择决策与出行者群体社会交互机制

为了便于对本文所提出票价优化方法的效果进行多维度对比分析,在既有研究以及本文模型假设基础上,依次设计由简单到复杂的三种出行需求演化模型。

表1 从出行者出行方式选择决策与群体社会交互方式两个维度刻画了出行需求的形成与演化机制。其中,为便于对比,模型1a 表示传统的基准logit 模型,模型1b 以传统logit 模型为基础,引入累积前景效用,假设所有出行者具有相同的参照点,即同种出行方式在同一时刻对所有出行者具有相同的效用(模型1 为基准比较模型)。模型2 假设出行者具有异质的参照点,对同种出行方式效用的感知存在差异,并且出行者之间的心理账户可以通过社会交互相互影响。模型3 的设计思想受到经典Bush Mosteller 模型的启发,出行者对出行方式的选择不仅受到当期效用的影响,还受到该出行方式票价调节过程及历史出行效用的影响,在此基础上,出行者之间的心理账户又通过社会交互相互影响。可见,从模型1b 到模型3,出行者群体的行为复杂性不断增加,异质、群体互动特征对群体决策的影响不断增大。

表1 出行需求演化模型Table 1 Travel demand evolution model

进一步,图3 给出了本文提出票价优化模型的整体结构,相比于传统票价优化双层规划问题,本文一方面将上层规划中目标出行方式i的票价优化模型改进为深度强化学习过程,另一方面则针对深度强化学习对复杂环境的适应特点,在下层规划中引入了出行者群体复杂决策机制。

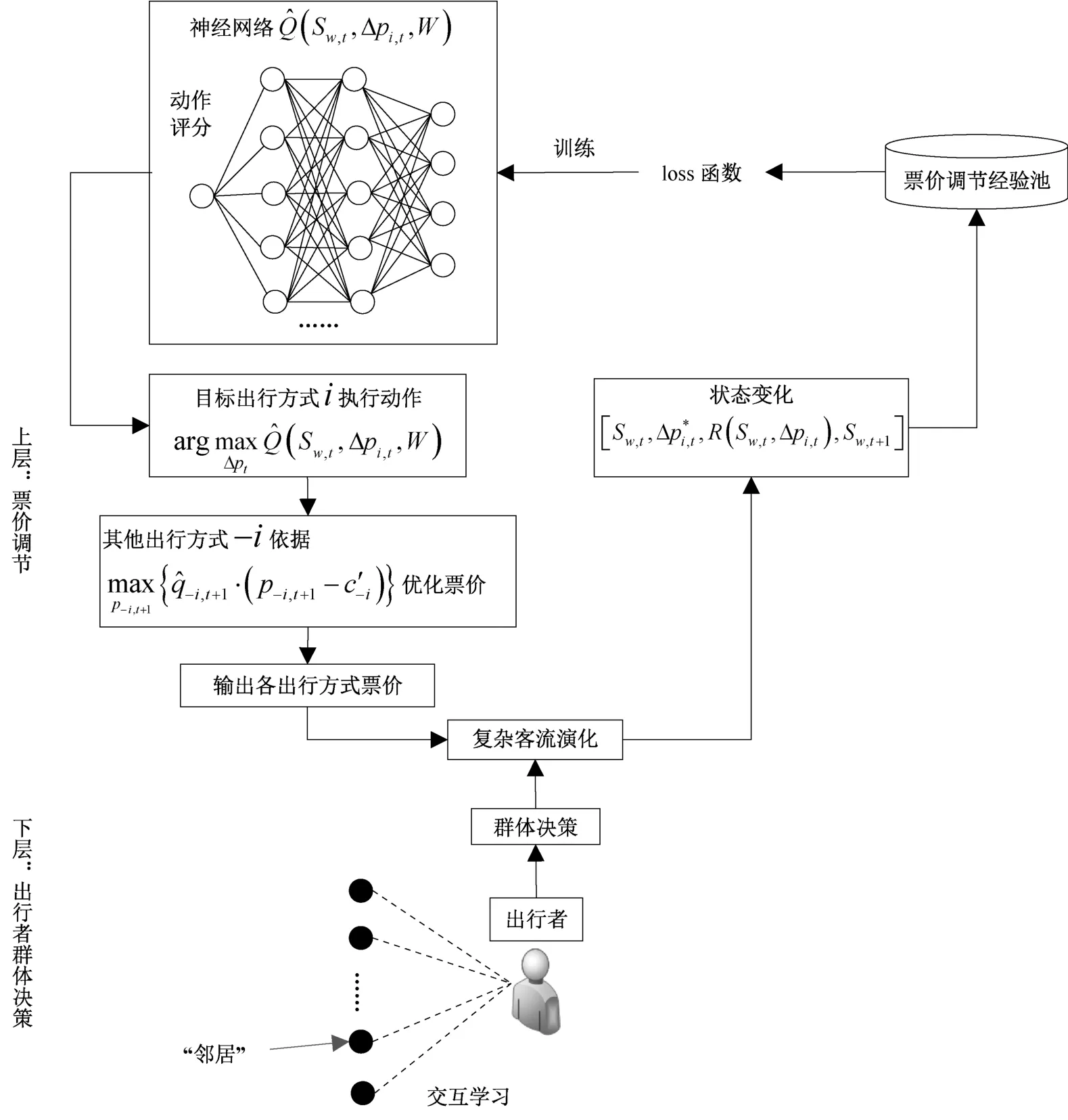
图3 引入DQN 的票价优化模型结构与实现流程Figure 3 Structure and implementation process of fare optimization model based on DQN

3 数值模拟与模型对比

3.1 出行场景与基础参数设置

地铁与地面公交是两种典型的城市公共交通出行方式,二者往往分属不同的运营主体,且在线路的选择与设计上考虑的因素又相近,因此在较多重叠的OD 区间内二者的发展依然会伴随着竞争关系[1,25]。在多种外部变量(票价方案、不同时段行程时间、舒适度、便捷性等)及出行者内生变量(参照点、信息交互)影响下,其客流演化具有复杂性。因此,本文将连接北京市主城区与通州副中心的地铁六号线东四到通州北关段作为两站点之间出行活动的建模背景,将对应于该线路区间的票价信息、行程时间等数据带入基于DQN的双层规划模型进行计算。如1.4 节所述,为了便于对比分析基于深度强化学习的票价优化方法产生的优化结果,令地铁与公交分别单独作为本文的目标出行方式,其票价采取基于深度强化学习的优化方法,另一种出行方式票价采用传统双层规划模型进行优化,数值模拟环境为Matlab2018。如后文无特别说明,参数取值均如表2 所示。

表2 中,地铁与公交的票价初始值与单位成本取值依据为北京市地铁与公交常见的平均价格,价格单位为人民币元;票价取值区间上限设置为本文算例选取行程区间(北京地铁六号线东四到通州北关段)目前市场票价的两倍,由于地铁具有更高的建设运营成本,故设置更高上限;行程时间取值依据本文算例选取行程区间地铁与公交的行程时间的真实数据得到。进一步,公交车在行程时间、舒适度等效用的稳定性上劣于地铁,因此设置φ1＜φ2;出行者群体损失规避系数,决策权重函数以及决策权重函数系数依据文献[23-24]取值,即λ=2.25,α=β=0.88;出行者对效用的记忆长度m以连续工作日长度(5 天)为基准设置;Logit 模型效用感知系数θ依据文献[25]中无私家车通勤者的效用系数近似得到;为保证出行费用中的各项具有相同的数量级,ξh与ξc取值0.03;依据本文出行场景,Q 值神经网络输入层神经元数量为5,设置两个隐含层,依据Kolmogorov 定理,隐含层神经元数量为11(“2*输入层神经元数量+1”原则)。

表2 基本参数设置Table 2 Basic parameter setting

此外,票价调节动作变量Δpi,t的决策空间做如下设置:Δpi,t∈{在pi,t的基础上降价5%,在pi,t的基础上降价1%,票价不变,在pi,t的基础上提价1%,在pi,t的基础上提价5%}。

3.2 票价优化结果

针对出行需求演化模型1～模型3 设置相同的基本参数环境,不同的模型代表着不同复杂程度的群体出行需求,基于不同的出行需求演化机制,运行引入DQN 的票价优化模型,得到票价与出行需求随票价调节的演化结果(图4,图5,表3)。

由图4(a)～(d)与图5(a)～(d)可见,对于出行需求演化模型1a、1b 与模型2,票价与出行需求在大幅波动后趋于平稳,250 步训练后票价与出行需求的演化逐步收敛于稳定区间,体现了深度强化学习算法作用下不同票价调节动作在决策空间内的探索和收敛过程。而对于出行需求演化模型3,不难发现,相对于logit 模型,由于模型3 的出行行为演化动力为历史出行经验记忆与交互机制的共同作用,具有不完全信息特点,客流演化呈现规律性与随机性相互交织的剧烈震荡,流量分配结果与logit 分流模型(模型1 与模型2)产生了显著差异(图4(c)(d)与图5(c)(d)),该剧烈震荡并未影响深度强化学习算法得到票价输出的稳定性(图4(a)与图5(a)),而针对出行需求演化模型3 的传统双层规划方法得到的票价(图4(b)与图5(b))却出现剧烈波动现象。在深度强化学习算法中,票价的输出是由经验池中不断变化的出行需求环境对票价调节动作的训练得到,多次对需求环境的迭代“试错”提高了神经网络的泛化能力,从而使神经网络的输出趋于稳定,而对于传统双层规划方法,由(3)(4)式可知,票价的优化结果会受到当期客流震荡的影响,这说明相对于固定模型驱动下的优化方法,训练数据驱动下的DQN 方法在感知复杂出行需求方面具有优势。

图4(e)与图5(e)给出了票价调节训练过程中奖励值随着训练次数增加呈现整体上升的变化趋势,奖励值的上升说明票价调节动作在训练过程中寻找到了使目标出行方式收入增加的有效路径,体现了DQN 算法的智能性;图4(f)与图5(f)给出了群体行为具有复杂性的条件下(模型2 与模型3)群体风险态度这一重要参数与最终平均出行效用之间的变化趋势,该变化趋势符合累积前景理论中的参照点依赖图像[26],说明神经网络输出的票价调节机制并未使出行者的群体行为复杂性偏离参照点依赖,符合行为科学特征,即价值函数神经网络对于群体决策参数具有鲁棒性。综合上述结果可知,深度强化学习算法在本文提出的四种不同出行需求演化环境下均呈现出训练的有效性。

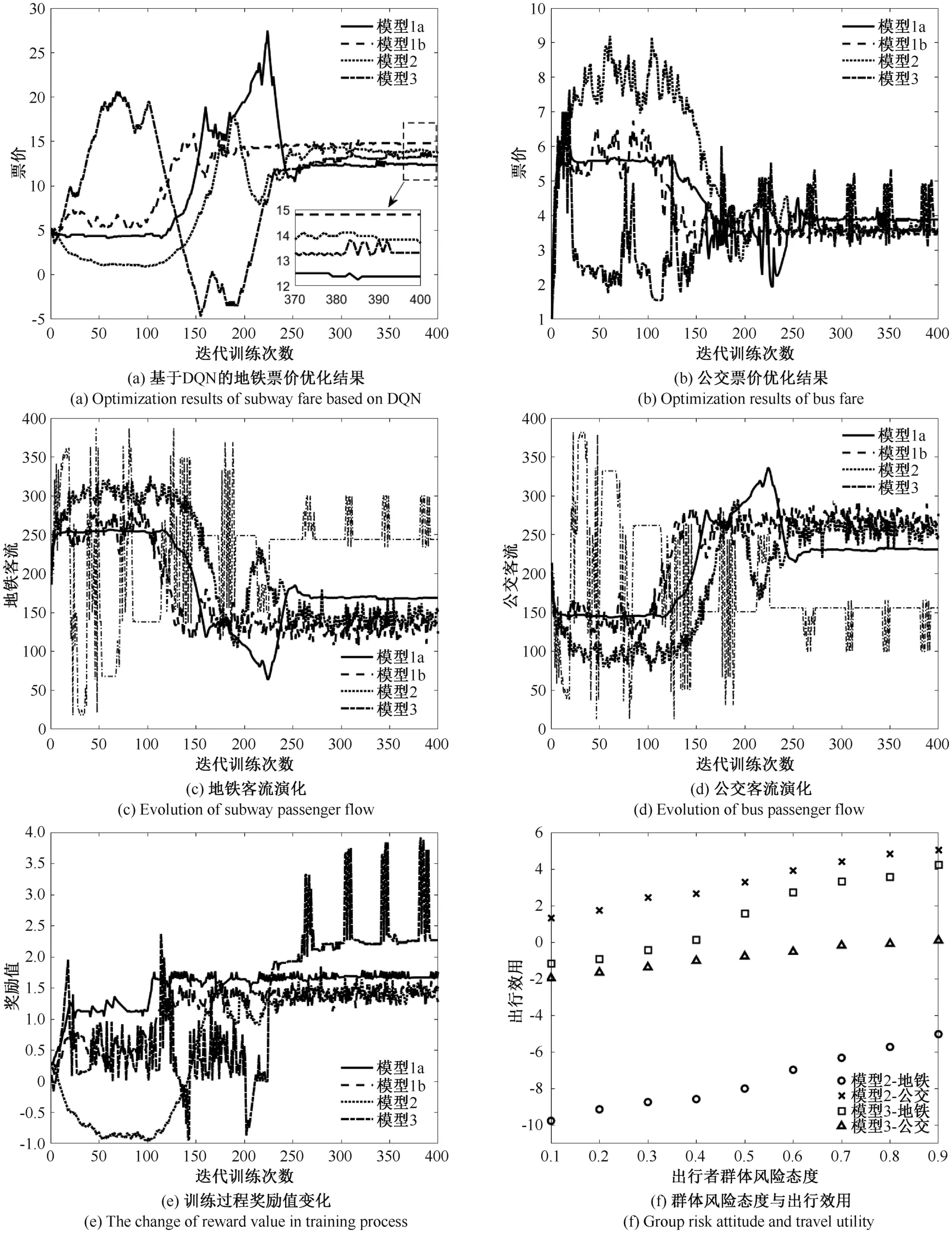
图4 基于DQN 的票价优化及客流演化结果(地铁作为目标出行方式)Figure 4 Ticket price optimization and passenger flow evolution based on DQN (Taking subway as the objective travel mode)

表3 给出了演化趋势稳定后的平均票价,由表3 可见,在传统双层规划中,运用线性近似估计客流量使各个出行方式的目标函数在广义Nash 均衡的作用下具有较强的相关性,而采用DQN 方法分别优化不同的目标出行方式,相当于更换了DQN 方法的目标函数,因此得到了差别较大的价格计算结果,这也说明不同运输方式之间具有显著差异化的利益最大化价格结构。此外,结合图4(a)、图5(a)可知,在深度强化学习算法的作用下,不同的出行需求演化机制对应于具有显著差异的票价测算结果(12.37 元～14.81 元,4.90元～6.35 元);而沿用了传统双层规划方法的票价(图4(b)、图5(b)及表3)在不同的出行需求演化机制作用下得到了近似的测算结果(集中于3.52～3.89 元,5.71～6.78 元)。上述结果均说明,随着出行需求演化形式复杂程度的变化,以神经网络为出行需求感知工具的深度强化学习算法具有更加细致的票价弹性刻画能力,在处理复杂出行需求时具有更好的效果。

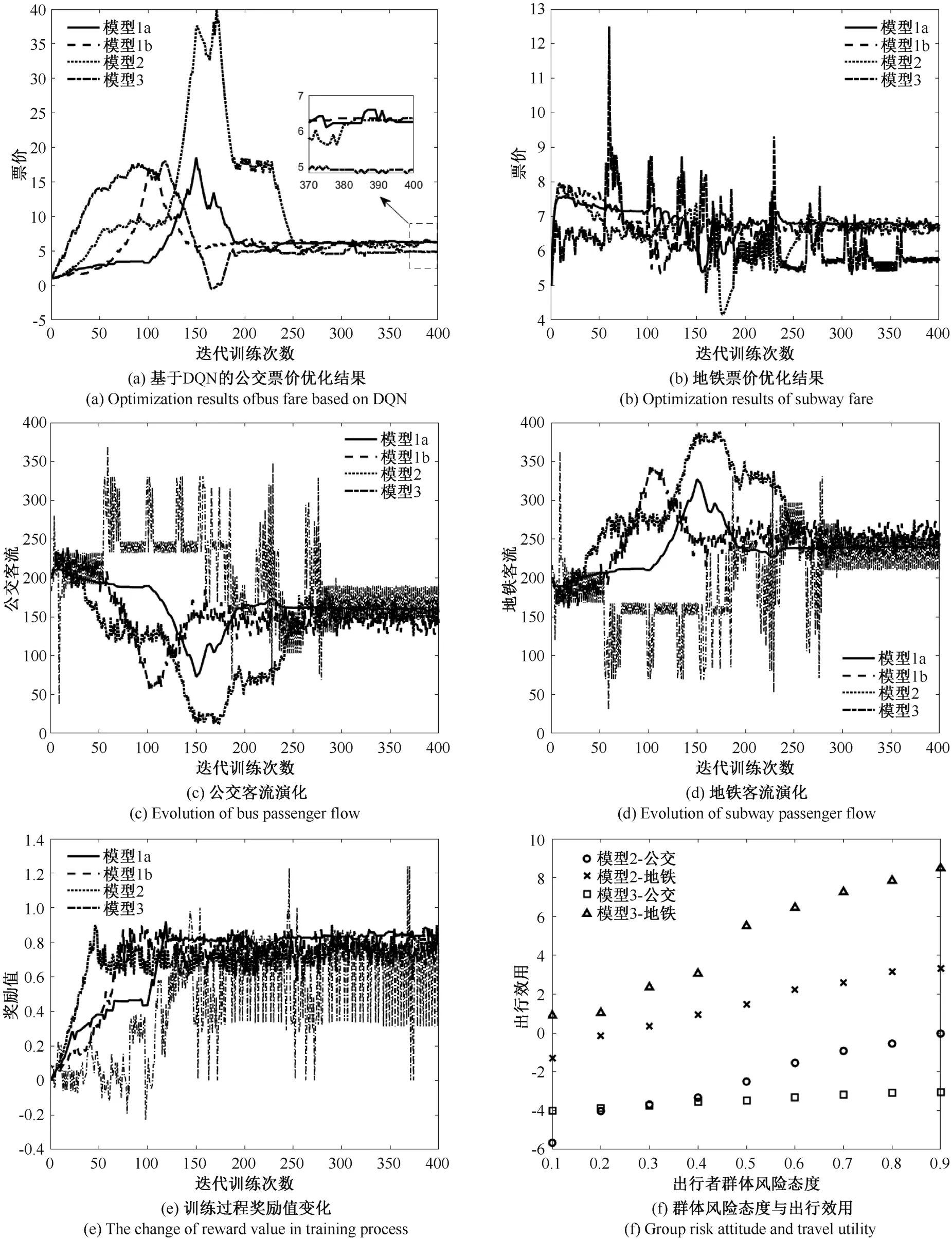
图5 基于DQN 的票价优化及客流演化结果(公交作为目标出行方式)Figure 5 Ticket price optimization and passenger flow evolution based on DQN (Taking bus as the objective travel mode)

进一步,在相同的参数条件下,将本文目标出行方式的优化方法更换为传统双层规划方法(即按照优化问题(3)式求解),针对地铁与公交票价,比较传统双层规划方法((3)式)与引入强化学习的优化方法((4)式)得到的票价、客流、利润测算结果,同见表3。

图6 给出了不同出行需求模型条件下传统双层规划方法得到的票价优化结果,可见,复杂的出行者群体决策使票价序列产生了不同幅度的波动,从出行需求模型1 到模型3,出行者决策机制越复杂,票价波动越大。结合图4(a)与图5(a)可知,神经网络强大的非线性特征拟合能力(复杂环境适应性)使深度强化学习算法得到的票价具有更好的稳定性。表3 的运算结果可知(对其中波动的票价序列取平均值):(1)与传统双层规划模型得到的结果相比,引入DQN算法优化票价后,两种出行方式的最优票价与出行需求结构产生了显著差异,DQN 算法得到的目标出行方式票价全部高于双层规划得到的最优票价,且对于不同的出行需求演化机制得出了差异化较大的票价(12.37 元～14.81 元,4.90 元～6.24 元);(2)在使用DQN 算法计算目标出行方式票价的条件下,未采用DQN 算法的非目标出行方式票价全部低于传统双层规划方法得到的最优票价,且在不同出行需求演化机制下票价相对集中(3.52 元～3.89 元,5.71 元～6.78 元);(3)在不同出行需求演化机制下,传统双层规划方法得到的最优票价差异最小(7.71 元～7.82 元,4.65 元～4.81 元),进一步说明深度强化学习算法具有更强的票价弹性刻画能力;(4)引入DQN 算法优化票价后,不同出行需求模型下目标出行方式的利润及两种出行方式的总体利润均得到显著增加,而未采用DQN 算法的非目标出行方式的利润则大多小于传统双层规划方法得到的利润。上述结果可知,相比于传统双层规划方法,DQN 算法通过对出行需求演化环境的适应性学习,实现了针对目标出行方式的利润增长,体现了该方法的智能特点。

图6 基于双层规划的票价优化结果Figure 6 Ticket price optimization results based on bi-level programming

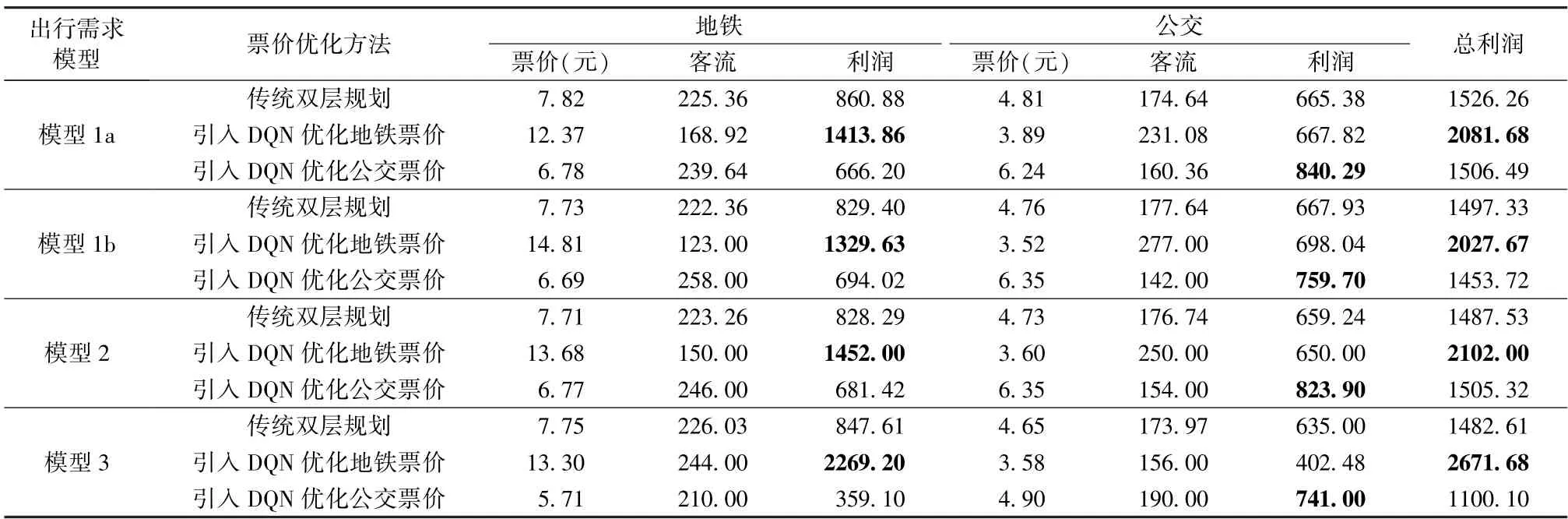
表3 不同优化方法对比Table 3 Comparison of different optimization methods

通过对比表3 中不同模型产生的客流分配结果可知,随着出行行为复杂性不断增加(从模型1 过渡到模型3),两种出行方式之间的客流量差异呈现递减趋势。这是由于,相比于logit 模型,BM 模型中的出行者更多依赖历史经验而无法及时掌握完全的效用信息,从而减弱了出行者群体在不同出行方式之间的分流力度,模型的演化结果较好地反映了这一现象,也更加接近实际情形下地铁与公交总体客流比例关系(北京市日均公交客运量900 万人次、地铁日均1000 万人次左右)。

此外,出行需求模型1b、模型2 及模型3 选用了相同的效用评价标准(累积前景效用)且出行者群体的行为复杂性递增,由表3 可知,从模型1b 到模型3,DQN 算法得到的利润与双层规划方法得到的利润之差呈现显著递增,并在出行需求模型3 条件下产生了最高总利润2671.68 元,这一结果反映了出行者群体行为复杂性的增加会使运营管理部门获得更高的收入[26]。

目前,本文所选取的建模背景(东四-通州北关段)在实际情形下的票价为:地铁票价5 元,公交票价为5-8 元。对比本文的计算结果可知,目前的实际价格更加接近DQN 方法下将公交作为目标出行方式得到的票价方案,这说明目前地铁票价存在较大程度的补贴,政府部门可依据财政补贴的预算额度提出地铁票价的指导价格。近年来,随着共享出行等新型客运服务模式的不断涌现,运营管理部门在实际的票价制定过程中,可针对不同运输方式的目标测算针对性的票价方案,择优选取。

4 结论与思考

本文在既有的交通系统票价优化研究基础上,针对群体出行需求演化复杂性,将票价的调节和优化过程视为一个在复杂社会经济系统中经过不断探索与尝试而获得最优价格的决策过程,引入人工智能领域的深度强化学习算法,在不同复杂程度的出行需求演化场景条件下实现了票价测算,数值模拟结果表明本文提出的方法在票价优化问题中具有较好的适用性。

由本文在不同出行需求演化模型下得到的强化学习训练结果可知,现实情形下,当考虑出行者群体决策复杂性时,群体出行需求与票价之间会呈现多样化的弹性关系。尤其是近年来,随着多种类型的网约车、共享单车乃至共享汽车等新型客运服务模式的不断涌现,群体出行需求的演化势必将呈现更加复杂的形式。显然,采用深度强化学习算法中的价值函数神经网络来拟合出行需求(环境)对票价调节(动作)的反应函数具有一定的实际研究价值,也是对既有票价测算方法的补充。

需要指出的是,为便于与既有的价格弹性刻画方式进行对比,本文构建的多种出行方式票价竞争场景,仅对其中目标出行方式的票价优化过程引入了深度强化学习方法,下一步的工作中,将进一步引入深度强化学习方法中的“左右互搏”与“对弈”机制,获取多种出行方式同时采用深度强化学习方法后产生的最优价格。另一方面,本文在深度强化学习算法的使用中仅考虑了单OD 对条件下以利润最大化为决策目标的交通场景,因此得到了较高的票价测算结果,这也说明现行票价体系存在较大幅度的补贴。在未来的研究中,将进一步在该方法的运用中考虑多OD 对的线网环境,并对多OD 对条件下的群体决策演化机理进行更为合理的设计。