考虑侧窗约束的模型预测静态规划末制导方法
权申明,晁 涛,张登辉,3,杨 明
(1. 哈尔滨工业大学航天学院控制与仿真中心,哈尔滨 150080;2. 上海机电工程研究所,上海 201109;3. 沈阳飞机设计研究所,沈阳 110031)
0 引 言
助推滑翔飞行器末段一般通过寻的导引方式实现精确制导。受实际物理系统约束,末制导阶段存在多种约束,如落角[1-2]、落速[3]等[4]。在助推滑翔飞行器的整个俯冲段,通过导引头探测目标信息,因此目标应始终位于导引头视场范围内。对于红外导引头,严重的气动加热导致其探测性能降低,因此将其安装在头部的侧面或下方。为满足视场约束,弹目相对位置与姿态需要满足特定的约束条件。
为了保证飞行器结构安全、姿态稳定,最终完成飞行任务,制导系统需要综合考虑飞行过程中的各种实际约束[5]。对于侧滑转弯(Skid-to-turn, STT)飞行器,过载约束可以转化为攻角和侧滑角约束。针对带侧窗探测导引头的飞行器,为避免气动加热对飞行器性能的影响,其攻角和侧滑角需要考虑实际约束条件。同时,执行机构由于幅值和速率等物理限制,如果在制导控制系统设计中没有考虑这些因素,则飞行器在实际飞行过程中可能会出现弹体失稳等严重后果,最终导致任务失败。基于上述分析,开展综合考虑攻角、侧滑角幅值及速率约束的带侧窗约束末制导研究,具有较强的工程意义。
文献[6-7]针对捷联导引头受限问题,基于对称障碍李雅普诺夫函数进行了制导控制一体化末制导律设计,捷联探测中视场约束是对称的,结合对称障碍李雅普诺夫函数方法可以取得较好的控制效果。红外导引头采用侧窗探测,文献[8-10]尝试通过优化方法与制导律解决非对称侧窗约束问题。
目前,考虑导引头侧窗约束的工作主要在纵向平面内进行制导律设计:通过假设攻角近似为零,将速度方向和弹目视线之间的夹角近似替代视场角,在模型建立与制导律设计中进行简化。对于末段依靠气动力实现精确制导的飞行器而言,以上假设难以成立,现有制导算法无法保证飞行器快速俯冲过程中始终满足侧窗视场约束。
自模型预测静态规划(Model predictive static programming, MPSP)由Padhi等[11]提出以来,在航天器制导控制[12-14]、软着陆[15]、轨迹跟踪[16]、再入制导[17-20]、末制导等方面有较多研究,在计算效率和制导精度上具有一定优势。后续研究中,过程中输入与状态约束逐渐引起关注[21-23]。文献[24]基于优化模型预测静态规划算法,针对吸气式高超声速飞行器设计了满足终端碰撞角约束的制导律。在此方法基础上,文献[25]考虑了飞行器避障问题。在MPSP的基础上,广义伪谱MPSP算法被提出[26],该方法进一步提高了算法求解速度与精度。
MPSP算法同模型预测控制有相似之处,MPSP算法需要不断基于原有轨迹进行小偏差线性化近似,初始轨迹的选取对优化结果有较大影响。
基于上述问题,本文提出一种考虑侧窗约束的模型预测静态规划末制导方法。首先,引入体视线坐标系,精确描述侧窗约束。然后,基于体视线坐标系下运动模型,在处理无过程约束MPSP算法的基础上,考虑侧窗视场约束,通过松弛变量与虚拟控制量,将有约束优化问题转化为无约束优化问题。最后,通过不同仿真场景、不同优化方法的仿真与分析,验证本文所提算法的计算效率与精度。
1 问题描述
1.1 坐标系及转换关系
在考虑侧窗约束的末制导研究中,通常需要在体视线坐标系(Body line-of-sight, Body-LOS)和弹体坐标系以及视线坐标系进行模型建立与分析,三个坐标系的定义可参考文献[27]。

图1 体视线坐标系和弹体坐标系间的关系Fig.1 Body-LOS coordinate system with respect to body-fixed coordinate system
(1)

图2 体视线坐标系和视线坐标系间的关系Fig.2 Body-LOS coordinate system with respect to LOS coordinate system
采用视线滚转角γb描述视线坐标系到体视线坐标系的转换关系。
(2)
采用攻角α、侧滑角β描述速度坐标系到弹体坐标系的转换关系。
(3)
1.2 侧窗约束
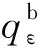
在传统的视线坐标系下考虑末制导问题时,侧窗探测约束为动态约束,与飞行器姿态相关,因此给制导控制设计带来困难。然而,在体视线坐标系中的问题,侧窗约束为时不变约束。因此本文将研究飞行器在体视线坐标系下的制导问题,这将导致制导控制与姿态控制之间的耦合。

图3 侧窗示意图Fig.3 Side-window diagram
1.3 飞行器运动模型
建立发射系下飞行器运动模型为
(4)
式中:x,y和z分别为飞行器在发射坐标系下位置分量;V,θ和σ分别为速度大小、弹道倾角、弹道偏角;g为重力加速度;D,L和Z分别为气动阻力、升力和侧向力。速度系下气动力分量为
(5)
式中:q为动压;Sref为参考面积。气动系数由数据表分段线性插值得到
(6)
式中:H为飞行高度。
1.4 相对运动模型
为了更加清晰的描述飞行器侧窗约束,描述体视线角的变化规律,在弹体坐标系中,飞行器M-目标T的相对速度v可表示为
(7)
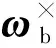
(8)
结合体视线坐标系定义,ωb可表示为
(9)
则
(10)
同理,飞行器-目标的相对加速度a为
(11)
忽略沿飞行器-目标视线方向的相对加速度,两侧求导后,体视线坐标系下相对运动方程可整理为
(12)
式中:aTx,aTy,aTz为目标加速度在体视线坐标系下分量;aMx,aMy,aMz为飞行器加速度在体视线坐标系下分量。
假设目标静止,可进一步整理式(12)得到矢量形式的弹目相对运动模型
(13)
飞行器合外力在速度坐标系下分量为
(14)
得到体视线系下的加速度分量为
(15)
2 算法设计
本节首先进行无过程约束MPSP算法介绍,在此基础上,提出考虑侧窗约束的MPSP末制导算法。
2.1 MPSP算法介绍
一般的非线性系统的状态动力学和输出方程可以写成
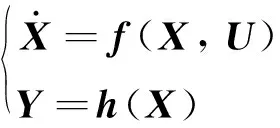
(16)
式中:X∈Rn,U∈Rm,Y∈Rp分别代表状态向量、控制向量和输出向量,其非线性动态模型的离散形式如下
(17)
式中:k表示第k个离散节点,k=1,2,…,N-1。
在一次MPSP计算中,主要分为以下五个步骤:
1)初始轨迹猜测
由于MPSP基于沿轨迹线性化的思想,逐步逼近最优解,因此在迭代计算过程中,需要初始轨迹作为算法启动条件,通常情况下,可将其设为常量。为了加快计算速度,减少迭代次数,可以基于其他算法,如:粒子群算法、伪谱法、凸优化等得到的初始轨迹进行后续迭代计算。
2)计算终端偏差
设期望终端状态为YNd,经过积分计算得到终端实际状态为YN,则终端偏差为
ΔYN=YN-YNd
(18)
MPSP的重点是如何找到一个合适的控制量,以便在最后一步的输出YN达到期望值YNd,同时花费最少代价。
3)灵敏度计算
式(18)泰勒展开得到
(19)
对式(17)线性化处理,得到
(20)
对于终端状态,存在
(21)
从而得到
(22)
(23)
将式(20)中状态量不断更新得到
dYN=AdX1+B1dU1+B2dU2+BN-1dUN-1
(24)
式中:
(25)
由于初始状态为给定值,则dX1=0。可得
(26)

4)控制量更新
由于MPSP基于初始轨迹进行沿轨迹线性化,因此每次迭代中,控制量的偏差dUk不能过大,否则灵敏度矩阵将难以准确描述输入量对终端状态约束的关系。选取性能指标为
(27)
同时,存在下述等式约束
(28)
结合最优控制理论,构造拉格朗日函数
(29)
其最优必要性条件为
(30)
联立解得
(31)
式中:
(32)
得到解析形式的控制量变化量
(33)
更新控制输入为
(34)
经过离散化模型更新状态量及输出量,得到Xk与Yk。
5)迭代计算
根据积分得到的终端状态与期望的终端状态偏差,计算其相对误差,若相对误差满足精度,则退出循环;否则以新的轨迹作为初始轨迹,跳转至步骤二循环迭代计算,直至相对误差满足要求。
2.2 考虑侧窗约束的MPSP末制导方法
考虑如下系统
(35)
存在侧窗视场约束
(36)
将约束转化为
(37)
将上式写为
(38)
式中:
(39)
记
(40)
引入松弛变量处理体视线角约束,假设
(41)
对式(41)求导,可得
(42)
式中:
(43)
进一步求导
(44)
式中:
(45)
将式(35)代入式(45)中,出现控制量
(46)
引入虚拟控制量uε,uβ,且
(47)
记x11=αε,x21=αβ,辅助变量的初始状态为
(48)
设计考虑侧窗约束制导算法流程如图4所示。
为了降低算法对初始轨迹的依赖性,提出逐次加入约束的求解步骤,第一次迭代中仅加入终端位置约束,得到优化解后,再增加过程约束。这种方法能够降低对初始轨迹的依赖,无需使用比例导引计算可行轨迹。
3 数值仿真及分析
为了验证本文所提算法的有效性与适应性,本节分别进行考虑侧窗约束MPSP末制导仿真、对比算法仿真以及适应性仿真实验。其中,对比算法仿真中选取的对比算法为文献[7]中障碍李雅普诺夫函数(Barrier Lyapunov function,BLF)算法。仿真初始条件和约束条件如表1~表2所示。

表1 仿真初始条件Table 1 Initial values of the simulation

表2 仿真约束条件Table 2 Constraints of the simulation
3.1 侧窗约束MPSP末制导仿真
侧窗约束MPSP末制导仿真结果如图5~图6所示。
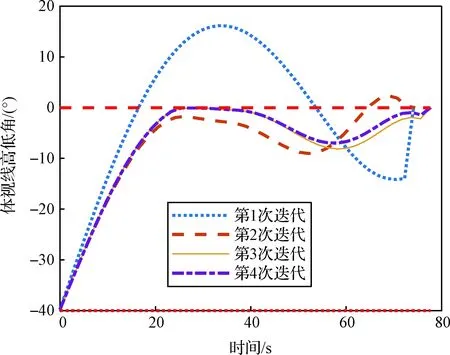
图5 体视线高低角变化曲线Fig.5 Body-LOS elevation angles

图6 体视线方位角变化曲线Fig.6 Body-LOS azimuth angles
考虑侧窗约束的MPSP算法能够实现对目标的精确打击,该末制导仿真场景中,攻角和侧滑角较小,因此合成攻角较小,气动阻力减速不明显;同时,飞行器高度下降较快。在考虑侧窗约束的MPSP算法中,第一次迭代仅考虑终端位置约束,因此体视线高低角和方位角约束没有满足;在位置约束满足后,由图5第2~4次迭代结果可以看出,体视线高低角约束满足要求,该算法在4次迭代后满足精度要求。
3.2 对比算法仿真
同基于BLF算法进行对比仿真,结果如图7~图9所示。
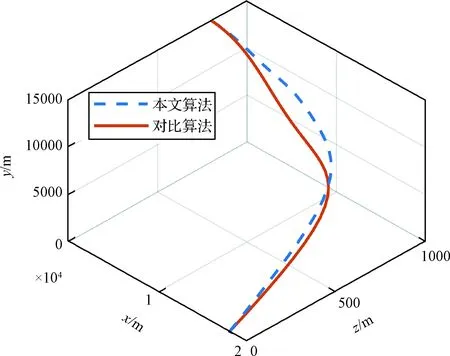
图7 三维轨迹Fig.7 3D trajectories
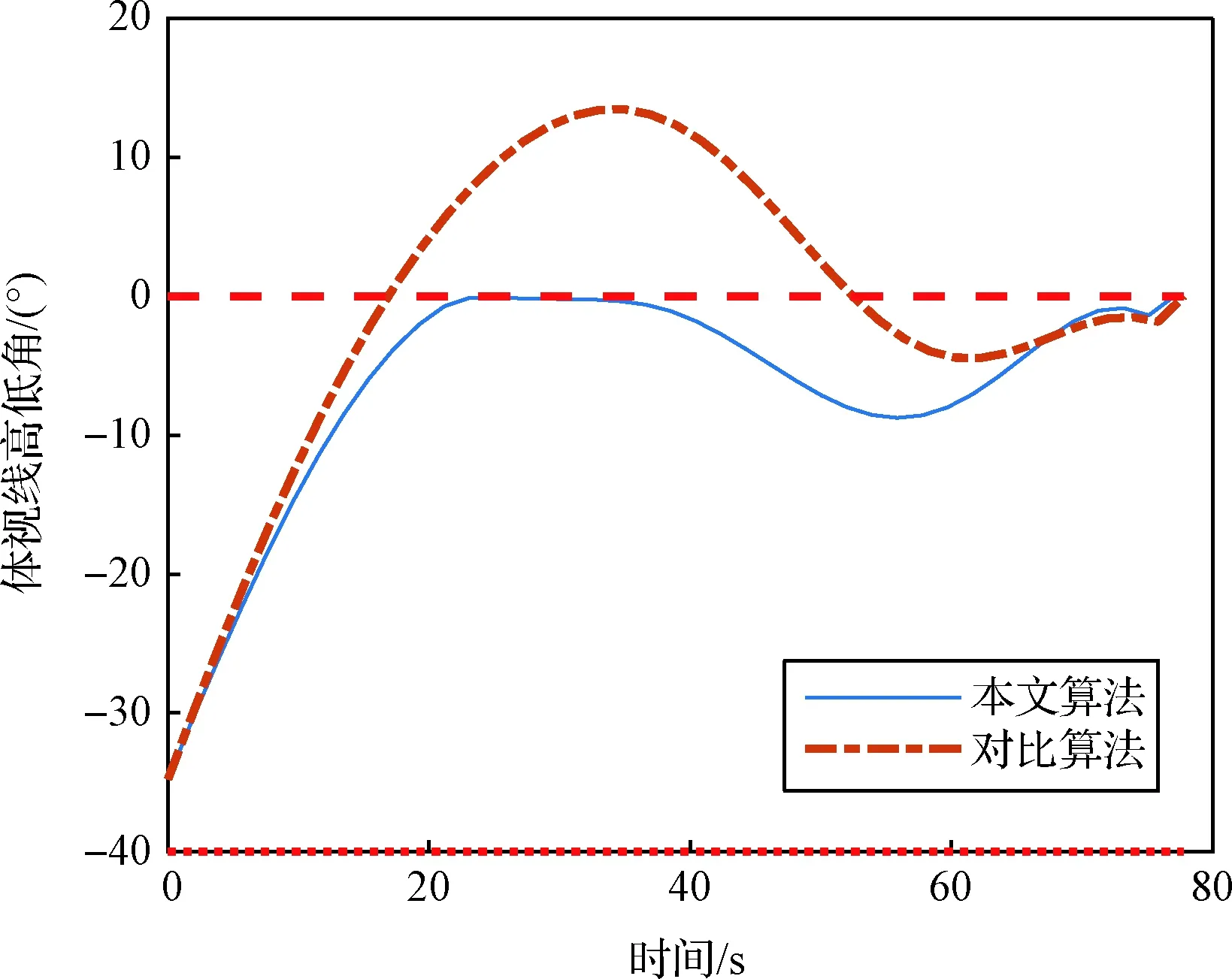
图8 体视线高低角变化曲线Fig.8 Body-LOS elevation angles

图9 体视线方位角变化曲线Fig.9 Body-LOS azimuth angles
由图7可以看出,两种方法均能满足终端位置约束,而对比算法用于处理对称视场约束,因此图9中体视线方位角能够满足要求,但难以处理本文中非对称侧窗约束。由图8可以看出,本文方法更具优势。
由于BLF制导律难以满足体视线高低角约束,为了进一步说明本文算法的优越性,与基于凸优化方法进行对比,对比结果如表3所示。

表3 不同算法对比结果Table 3 Simulation results of different algorithms
由上表可以看出,三种算法在终端位置精度上均小于0.5 m,能够获得较小的脱靶量。整体上,基于BLF方法的仿真耗时较小,但是违背侧窗视场约束后,无法测得目标信息,实际仿真中难以保障成功率。相比于凸优化方法,本文算法的优化变量仅有控制量或者虚拟控制量,而凸优化方法中将多个状态变量、控制量均作为优化变量,因此仿真耗时上本文算法更具优势。
3.3 算法适应性仿真
为了验证本文所提算法对不同仿真初始条件的适应性,设计以下4组算例进行仿真,仿真结果如图10~图12所示。

表4 算法适应性仿真初始条件Table 4 Initial conditions in the algorithm adaptability simulation
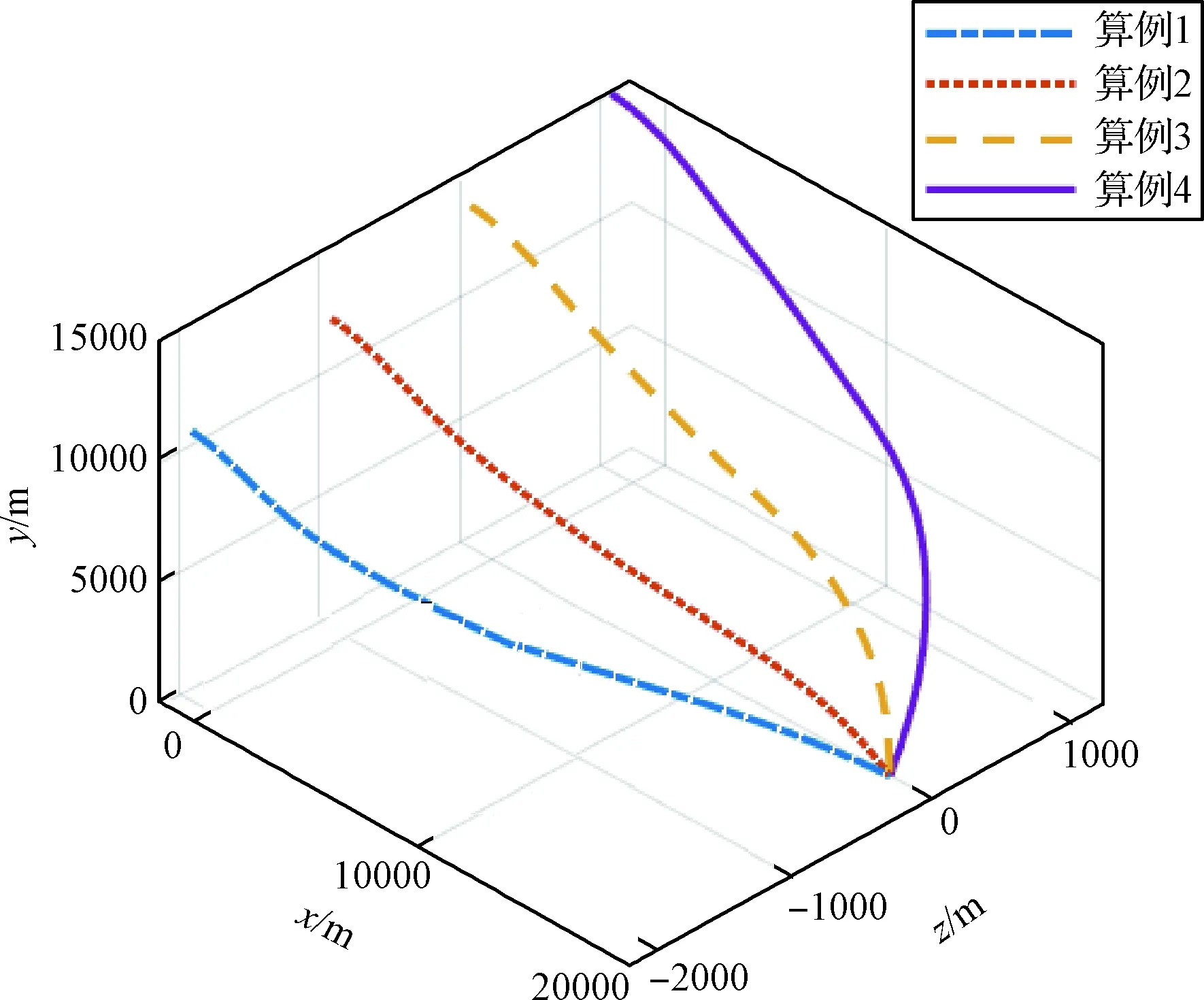
图10 三维轨迹Fig.10 3D trajectories
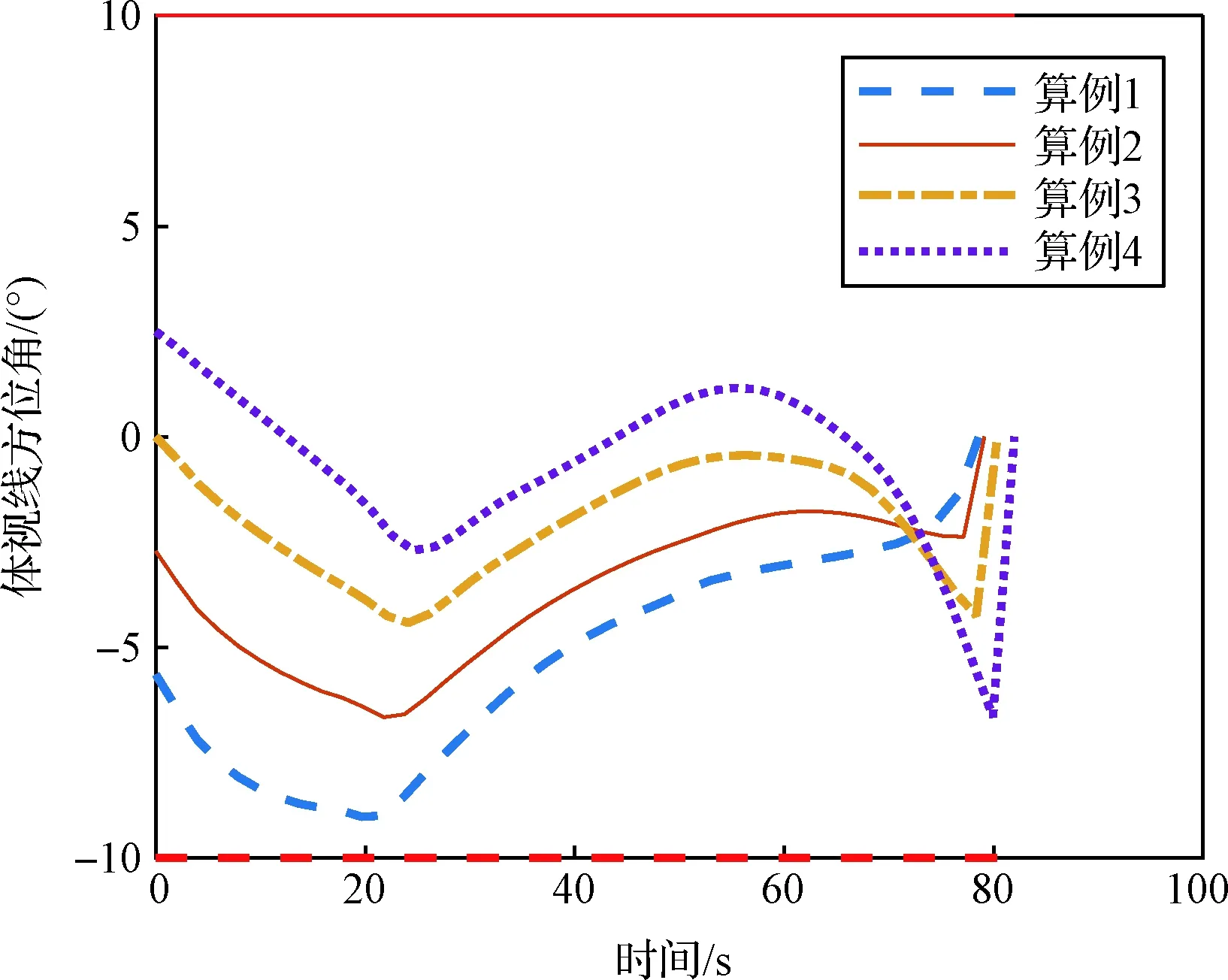
图11 体视线高低角变化曲线Fig.11 Body-LOS elevation angles

图12 体视线方位角变化曲线Fig.12 Body-LOS azimuth angles
可以看出,体视线高低角变化相对平缓,虽然体视线方位角在末段时有较为明显的变化,但是此时飞行器已经接近目标,一部分原因是弹目距离较小引起的角度计算变化过快。攻角和侧滑角幅值较小,减轻了姿态环控制器的控制压力。在4组仿真算例中,体视线高低角、方位角均能满足约束。
4 结 论
本文提出了一种考虑侧窗约束的模型预测静态规划末制导方法。在体视线坐标系建立了三维飞行器-目标相对运动模型,引入松弛变量与虚拟控制量处理侧窗约束,并提出了逐步增加约束条件的计算策略,降低末制导算法对初始猜测轨迹的依赖性。主要结论如下:
(1) 引入体视线坐标系,得到体视线坐标系下的运动模型,可以精确描述侧窗约束。
(2) 通过松弛变量与虚拟控制量,可以将考虑侧窗视场约束优化问题转化为无约束优化问题。
(3) 为了解决传统MPSP算法过于依赖初始轨迹的局限性,提出逐步增加约束条件的迭代求解流程,从而使得小偏差线性化更具合理性,算法稳定性更强。
在本文算法的基础上,后续将深入进行考虑侧窗约束末制导的在线制导仿真,同时,为了验证本文算法的工程适用性,将在六自由度模型中进行仿真与分析,考虑弹体姿态运动对制导精度的影响,从而实现完整的制导控制一体化。

