多臂凿岩机器人的碰撞检测方法研究
方梦娟,徐巧玉,李坤鹏,张 正
(1.河南科技大学 机电工程学院,河南 洛阳 471003;2.洛阳银杏科技有限公司,河南 洛阳 471003)
0 引言
目前,多臂凿岩机器人广泛应用于煤矿、隧道开挖等领域中。由于凿岩机器人属于工业液压重载型机械臂,具有多臂协作、结构复杂等特点,机械臂在隧道中作业时极易发生碰撞干涉现象,严重时会造成施工人员伤亡和极大的经济损失,因此多臂凿岩机器人的碰撞检测问题亟需解决[1-3]。
迄今为止,众多学者在凿岩机器人的碰撞检测方面进行的研究[4-12],主要分为基于外部传感器的碰撞检测方法、基于视觉的碰撞检测方法和通过几何建模实现的碰撞检测方法。对于工业液压重载机器人,由于使用几何建模实现的碰撞检测方法易于实现且处理数据效率高,所以应用广泛。该方法通常将机器人钻臂杆件进行模型简化,通过计算空间几何模型距离实现机器人的碰撞检测。文献[13-15]采用球体和胶囊体包围盒简化机械臂模型,能够实现有效的碰撞检测,但因机械臂关节机械结构的不规则性,使用球体包络会对检测精度造成一定的影响。文献[16-18]采用圆柱体包围盒简化机械臂模型,基于空间向量运算实现碰撞检测。文献[19-20]使用空间凸多面体模型对复杂物体进行建模,能够准确实现碰撞检测,但凿岩机器人所处隧道壁相对规则,用该种方法会降低机器人与隧道的碰撞检测效率。依赖几何建模展开的凿岩机器人碰撞检测研究多应用于凿岩机器人的多个机械臂之间,而凿岩机器人机械臂与隧道的碰撞检测研究较少,仍待深入研究。同时,在依赖几何建模实现的碰撞检测方法中,复杂的建模方法和计算方法会降低检测算法的效率和精度。
针对上述问题,本文提出了一种多臂凿岩机器人的碰撞检测方法,将凿岩机器人机械臂杆件简化为圆柱体包络盒,通过实时计算圆柱体包络盒间的距离,实现凿岩机器人自身的碰撞检测;将圆柱体包络盒投影在隧道壁面上,通过判断矩形投影与隧道壁面凸多边形轮廓线的碰撞情况,实现凿岩机器人与隧道的碰撞检测。在中铁DJ3E凿岩机器人上进行实验,以验证算法的实时性和准确性。
1 凿岩机器人碰撞检测模型
本文以中铁DJ3E多臂凿岩机器人为对象展开研究,建立碰撞检测模型。该凿岩机器人如图1所示,共有4条机械臂:左中右3条工作钻臂和1条吊篮臂。
多臂凿岩机器人在隧道工作中碰撞现象,通常发生在单个钻臂杆件间、钻臂之间、钻臂和吊篮臂之间、钻臂和隧道面之间,如图2所示,共包含12类碰撞检测内容。
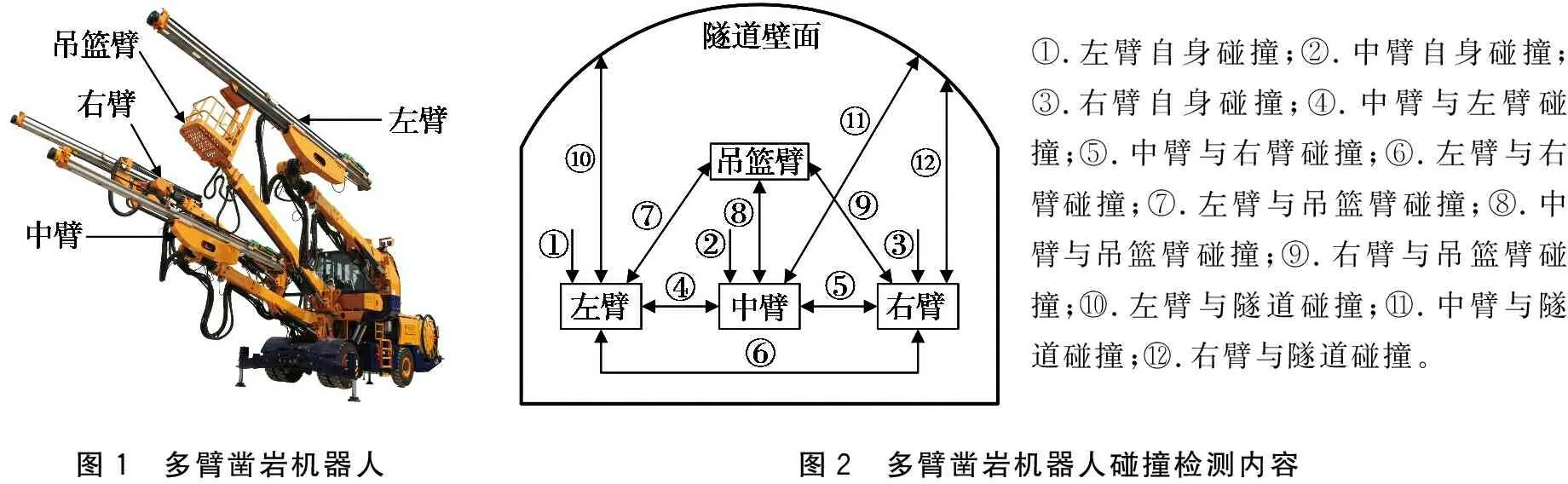
①.左臂自身碰撞;②.中臂自身碰撞;③.右臂自身碰撞;④.中臂与左臂碰撞;⑤.中臂与右臂碰撞;⑥.左臂与右臂碰撞;⑦.左臂与吊篮臂碰撞;⑧.中臂与吊篮臂碰撞;⑨.右臂与吊篮臂碰撞;.左臂与隧道碰撞;.中臂与隧道碰撞;.右臂与隧道碰撞。图1 多臂凿岩机器人图2 多臂凿岩机器人碰撞检测内容
由于凿岩机器人机械臂结构复杂,实际结构模型很难描述,因此建立3条钻臂和吊篮臂的包络盒模型,如图3所示。凿岩机器人三臂的简化模型一致,将钻臂杆件简化为4个圆柱体包络盒,机械臂关节包含于圆柱体包络盒中。由于在实际作业时,包络盒CS3所占空间范围较小,几乎不发生碰撞,因此CS3包络盒忽略不计,不参与碰撞检测。此时的碰撞检测模型更加简洁,有利于提高碰撞检测效率。同理,将吊篮臂的杆件简化为两个圆柱体包络盒。
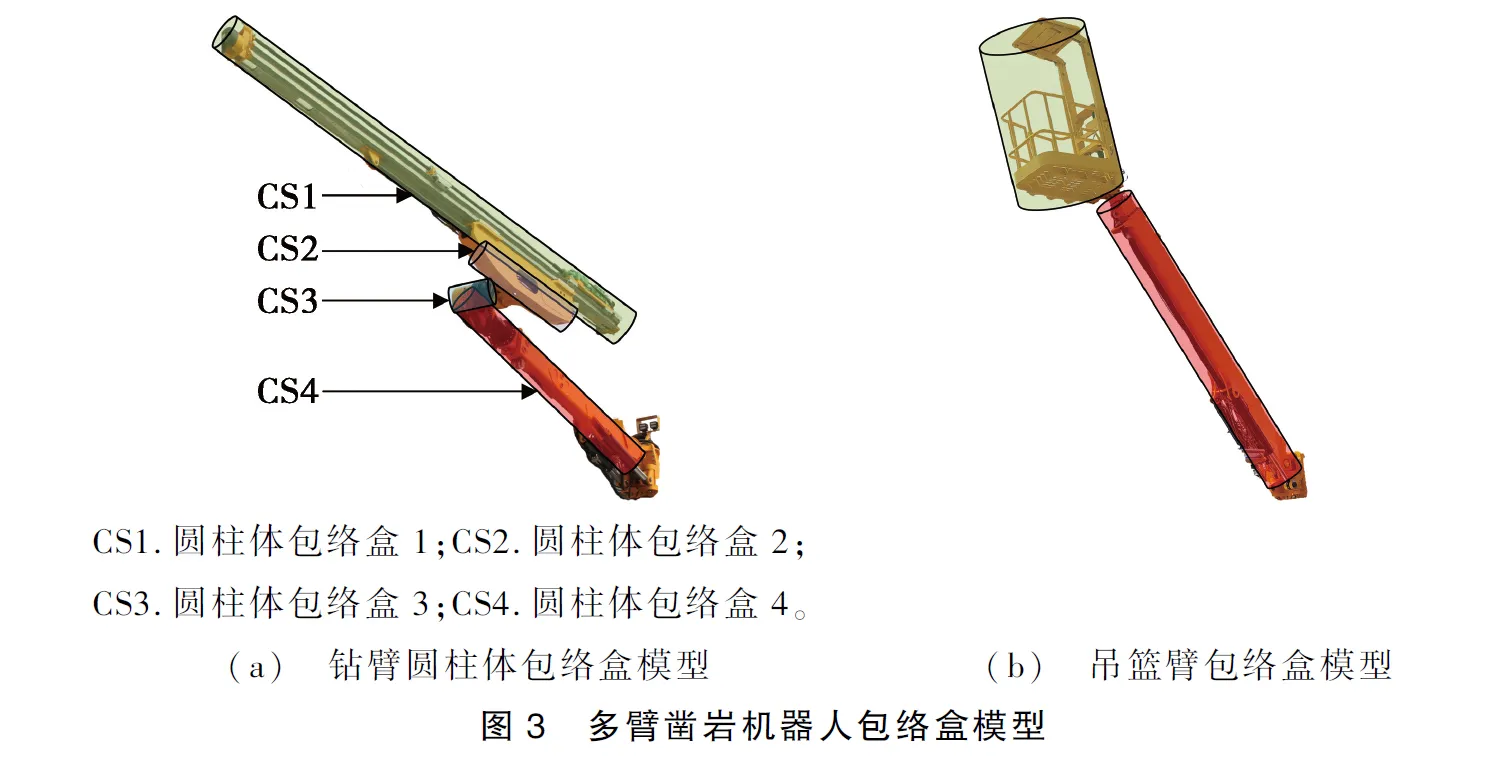
凿岩机器人自身的碰撞检测等同于求解空间圆柱体包络盒间的最小距离问题;将隧道模型简化为平面凸多边形,机器人钻臂与隧道碰撞检测等同于求解各圆柱体包络盒与隧道简化模型的碰撞问题。
2 碰撞检测算法
2.1 两圆柱体包络盒碰撞检测算法
将多臂凿岩机器人每条机械臂上的杆件简化为圆柱体包络盒后,通过计算圆柱体包络盒间的最小距离判断凿岩机器人自身的碰撞情况。
两圆柱体轴线段最小距离计算方法如下:
设两圆柱体包络盒的轴线段为l1、l2,底面半径为r1、r2,4个端点坐标分别为P1(x1,y1,z1)、P2(x2,y2,z2)、Q1(x3,y3,z3)、Q2(x4,y4,z4),如图4所示。记向量p=P2-P1,向量q=Q2-Q1,线段l1、l2上任意一点坐标用这两个向量表示为:
(1)
其中:0≤λ1;λ2≤1。
线段之间的最短距离可以转化为有约束的最优化问题,如式(2)所示:
minf(λ1,λ2)=[P(λ1)-Q(λ2)]2=[(P1+λ1p)-(Q1+λ2q)]2。
(2)
(3)
如图4所示,当0≤λ1,λ2≤1时,表示两直线的公垂线垂足落在两条线段中,则此时的最短距离d2=f(λ1,λ2);当λ1,λ2有一个不在[0,1]时,则表示两个垂足至少有一个没有落在线段内,此时分别求解P1到l2的距离d1、P2到l2的距离d2、Q1到l1的距离d3、Q2到l2的距离d4,两圆柱体轴线段最小距离d={d1,d2,d3,d4}min。
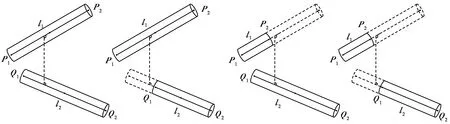
(a) λ1,λ2∈[0,1] (b) λ1∈[0,1],λ2∉[0,1] (c) λ1∉[0,1],λ2∈[0,1] (d) λ1,λ2∉[0,1]
已知两圆柱体底面半径分别为r1、r2,两圆柱体轴线间最小距离d,则圆柱体之间的最小距离dmin=d-(r1+r2),当dmin>0时,两圆柱体不发生碰撞,否则碰撞现象发生。该方法基于空间向量运算实现,避免了求解直线方程等复杂过程,便于通过C语言和MATLAB软件代码实现,提高了运行效率和检测精度。
2.2 圆柱体包络盒与隧道轮廓碰撞检测算法
隧道壁面简化为由直线段和圆弧线段组成的凸多边形,隧道轮廓简化模型如图5所示,同时将空间圆柱体投影到隧道壁面上,通过对圆柱体的投影矩形与隧道直线段、圆弧线段碰撞判别实现钻臂与隧道的碰撞检测。
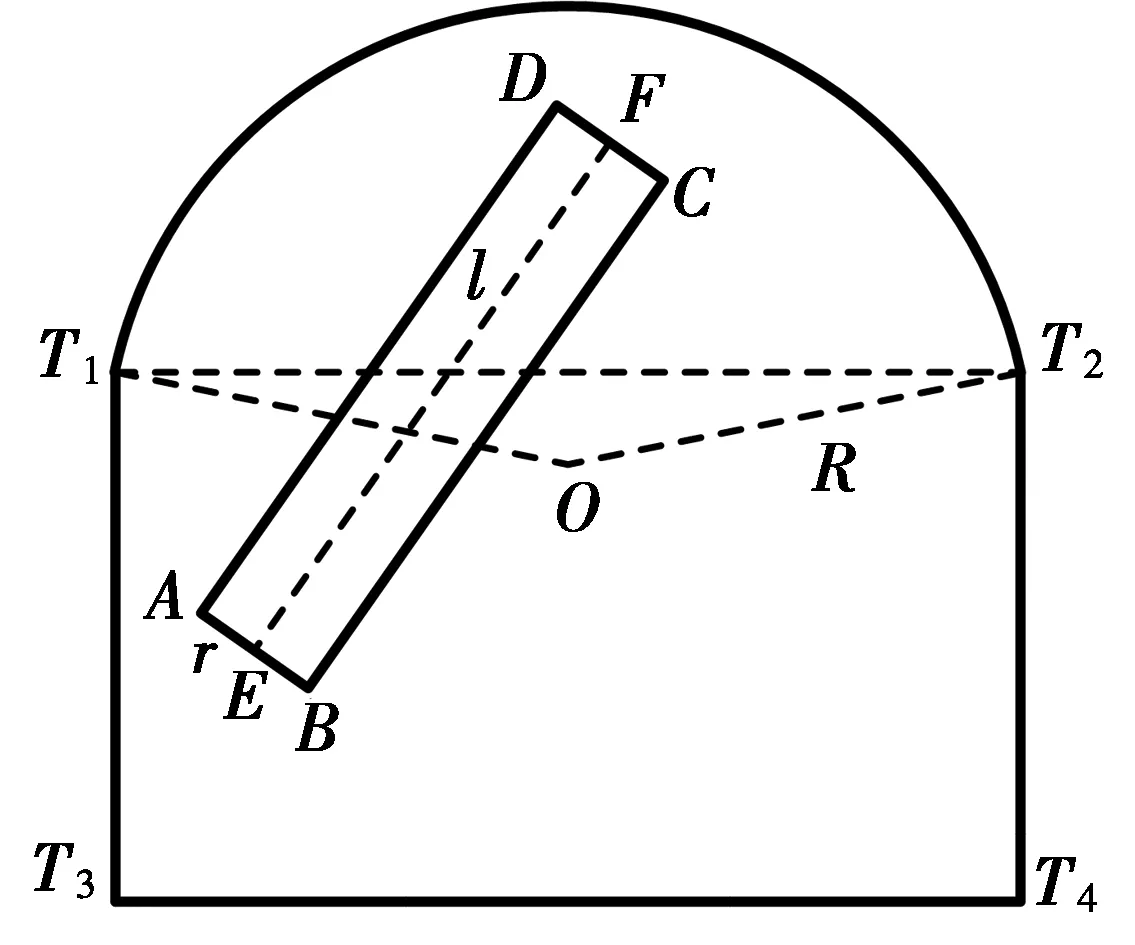
T1T3.隧道壁面的左轮廓直线; T2T4.隧道壁面的右轮廓直线; T3T4.地平面; O.圆弧T1T2的圆心;R.圆弧半径;矩形ABCD.圆柱体在隧道壁面的矩形投影;E、F.圆柱体轴线两端点;l.圆柱体轴线;r.圆柱体底面半径。
圆柱体的矩形投影与直线的碰撞检测分析:
如图5所示,通过计算矩形投影ABCD分别与直线T1T3、T2T4、T3T4的最小距离,反映圆柱体与直线的碰撞情况。已知圆柱体底面半径r,设轴线l与各直线的最小距离为d5,当d5 轴线l与各直线的距离计算方法参考上文两圆柱体轴线段最小距离计算方法。 圆柱体的矩形投影与圆弧碰撞检测分析: 矩形投影在扇形T1OT2上的分布情况见图6。如图6所示,矩形投影与圆弧的位置关系共有4种情况。 (a) 投影全部在扇形外 (b) 投影部分在扇形内 (c) 投影部分在扇形内 (d) 投影全部在扇形内 在以O为极点,射线OT2为极轴,逆时针方向为正的极坐标系中描述E、F、T1、T2这4个端点:E(‖OE‖,α1)、F(‖OF‖,α2)、T1(‖OT1‖,β1)、T2(‖OT2‖,β2),其中‖OT1‖=‖OT2‖=R,β2=0。 (Ⅰ)如图6a所示,矩形投影全部落在扇形T1OT2范围外,即E和F中最大极角小于T1和T2中的最小极角或E和F中最小极角大于T1和T2中的最大极角,此时矩形投影与圆弧线段无干涉发生。 (Ⅱ)如图6b所示,矩形投影部分落在扇形T1OT2范围内,T1和T2的最大极角介于E和F中最小和最大极角之间,且T1和T2的最小极角小于E和F中的最小极角,矩形投影轴线与扇形边缘的交点处为G,当‖OG‖ (Ⅲ)如图6c所示,矩形投影部分落在扇形T1OT2范围内,T1和T2的最小极角介于E和F中最小和最大极角之间,且T1和T2的最大极角大于E和F中的最大极角,矩形投影轴线与扇形边缘的交点处为G,当‖OG‖ (Ⅳ)如图6d所示,矩形投影全部落在扇形T1OT2范围内,当‖OE‖ 总结以上多种情况,可得矩形投影与隧道圆弧轮廓的碰撞情况如表1所示。 表1 矩形投影与隧道圆弧轮廓的碰撞情况 由上述分析及计算公式能够快速地检测出机器人钻臂与隧道的碰撞情况,通过在极坐标中判断极角区间的方式节省了算法的处理时间,提高了碰撞算法的检测效率。 利用中铁DJ3E凿岩机器人展开试验以验证碰撞检测算法的有效性。为保证试验安全性,将两圆柱体包络盒间的安全距离设置为100 mm,实时碰撞检测距离小于安全距离100 mm时,发生碰撞。 试验分为凿岩机器人自身机械臂碰撞检测、钻臂与隧道碰撞检测两大部分进行,其中,自身机械臂的碰撞检测包含了单个钻臂自身碰撞检测、两钻臂之间碰撞检测、钻臂与吊篮臂碰撞检测。 3.1.1 单个钻臂杆件间碰撞检测 为便于现场观察,使用凿岩机器人左臂进行试验。移动左臂并在MATLAB软件中计算钻臂各杆件是否发生碰撞,杆件间的实时最小距离如表2所示。图7为多臂凿岩机器人自身机械臂碰撞检测图。左臂最终状态如图7a所示,此时左臂关节值θl=[6.55,-3.28,0,0.57,-6.33,7.21,548],左臂自身将发生碰撞,DJ3E凿岩机器人显示器出现预警信号。 表2 MATLAB软件计算左臂自身碰撞检测结果 由表2和图7a可知:在左臂移动过程中,当左臂杆件间最小距离小于安全距离时,MATLAB软件实时计算结果表明钻臂将发生碰撞。 3.1.2 两钻臂之间碰撞检测 使用左臂和中臂进行试验,初始状态下无碰撞发生。移动左臂和中臂,并在MATLAB软件中计算钻臂是否发生碰撞,如表3所示。左臂和中臂的最终状态如图7b所示,左臂关节值θl=[-5.31,-8.52,0,2.01,-6.33,-3.42,548],中臂关节值θc=[-1.88,-14.91,0,1.05,5.61,7.27,501],左臂和中臂将发生碰撞,同时DJ3E凿岩机器人显示器出现预警信号。 由表3和图7b可知:在左臂和中臂移动过程中,当两臂杆件间最小距离小于安全距离时,MATLAB软件实时计算结果表明两钻臂将发生碰撞。 表3 MATLAB软件计算左臂与中臂碰撞检测结果 3.1.3 钻臂与吊篮臂碰撞检测 表4 MATLAB软件计算右臂与吊篮臂碰撞检测结果 使用右臂和吊篮臂进行试验。初始状态下无碰撞发生。移动右臂和吊篮臂,并在MATLAB软件中计算此时钻臂和吊篮臂实时最小距离,如表4所示。右臂和吊篮臂最终状态如图7c所示,此时右臂关节值θr=[-4.99,-30.88,1 285,-0.12,20.24,1.06,1 795],吊篮臂关节值θl=[-3.10,-7.62],右臂和吊篮臂间将发生碰撞,DJ3E凿岩机器人显示器出现预警信号。 (a) 左臂自身杆件间碰撞检测 由表4和图7c可知:在右臂和吊篮臂移动过程中,当两臂杆件间最小距离小于安全距离时,MATLAB软件实时计算结果表明两钻臂发生碰撞。 使用凿岩机器人右臂进行与隧道的碰撞检测试验,移动右臂使其逐渐靠近隧道顶部,并在MATLAB软件中计算此时右臂和隧道实时最小距离,如表5所示。右臂最终状态如图8所示,此时右臂关节值θr=[-2.71,-12.08,322,0.05,9.35,1.09,555],右臂和隧道墙壁之间将发生碰撞,DJ3E凿岩机器人显示器出现预警信号。 表5 MATLAB软件计算钻臂与隧道碰撞检测结果编号最小距离/mm是否碰撞1(初始状态)658.4否2(中间过程)491.8否3(中间过程)106.3否4(最终状态)<100是图8 右臂与隧道碰撞检测 由表5和图8可知:当右臂与隧道的最小距离小于安全距离时,MATLAB软件实时计算结果表明右臂与隧道发生碰撞。 上述试验在实体DJ3E凿岩机器人上完成,同时在MATLAB软件中进行机械臂的碰撞检测计算,将计算结果与实物碰撞结果进行对比验证,最终证明了该碰撞检测算法的实时性和准确性。 本文针对多臂凿岩机器人的结构和碰撞特点建立一种基于圆柱体包络的碰撞检测模型,提出一种空间两圆柱体碰撞检测方法、钻臂与隧道轮廓的碰撞检测方法,MATLAB软件仿真数据和现场试验数据证明,该检测方法可以快速且全面地检测凿岩机器人的碰撞情况。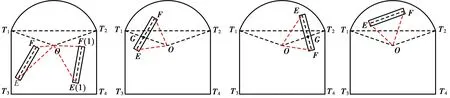

3 试验结果及分析
3.1 凿岩机器人自身机械臂碰撞检测
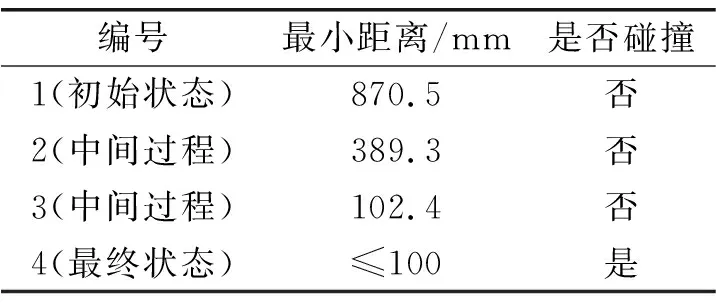
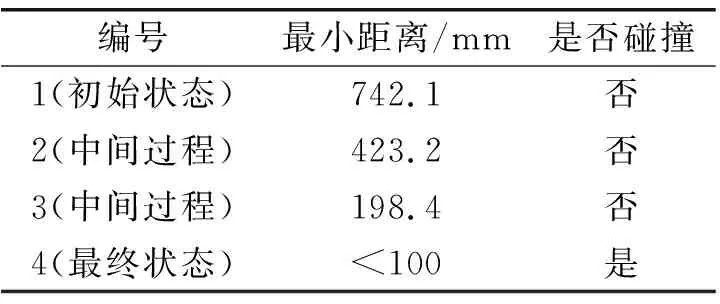
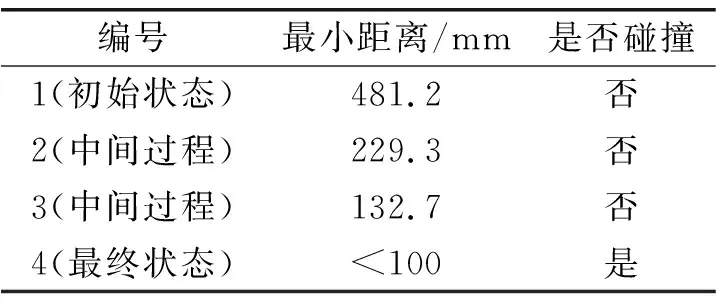

3.2 钻臂与隧道碰撞检测

4 结论

