一道截面问题的探究之旅*
林清利 吴晓明 曾献峰 (福建省莆田第一中学 351100)
在我校近期的一次考试中,学生在一道作截面图问题上得分不够理想.在批阅试卷过程中发现不少学生未作答或得分很低,同时发现存在多种解法,但有些解法是错误的.这引起了笔者的思考:为何一道看似简洁、直观、普通的试题得分情况却不理想?下面我们一同探个究竟.
题目如图1,三棱柱ABC-A1B1C1中,M是AA1的中点,过MC1作该三棱柱的截面α,使A1B∥α,写出作图步骤,并证明.
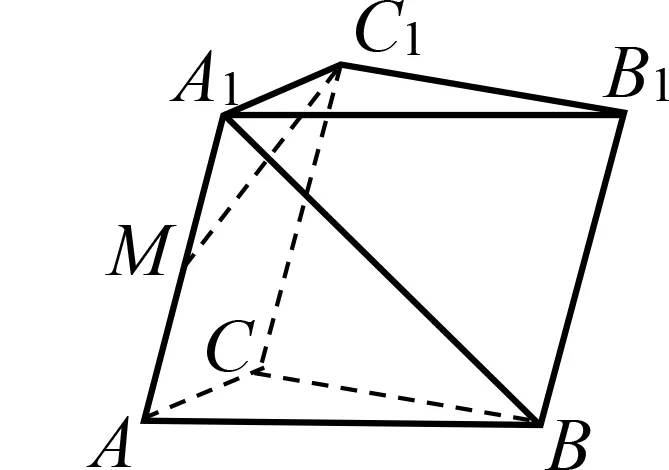
图1
1 错解分析
错解1 如图2,设AB中点为N,连结MN,则截面为△C1MN.
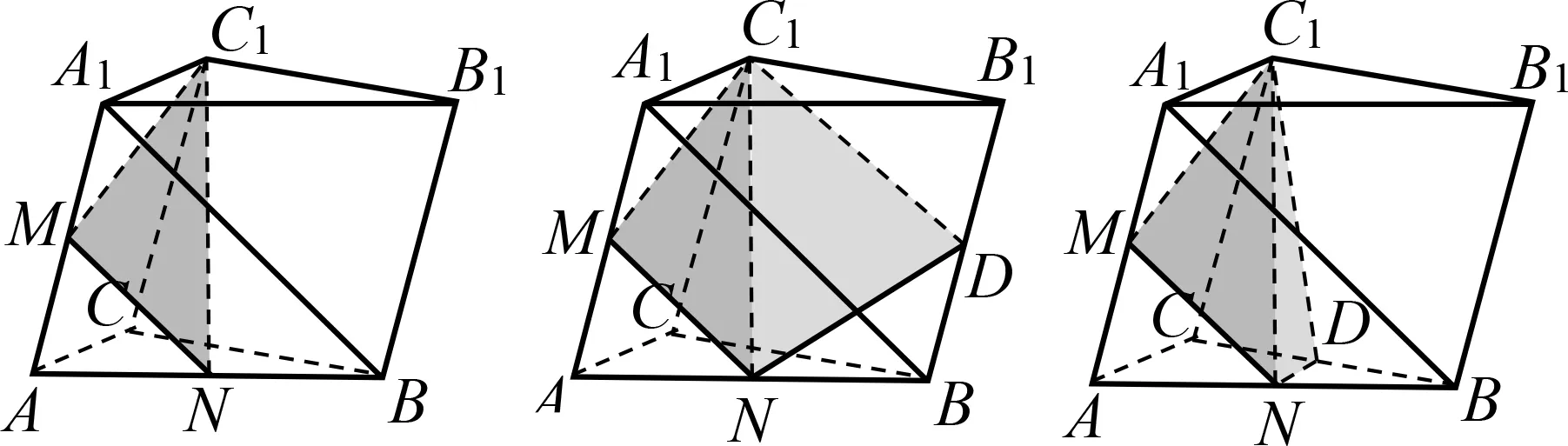
图2 图3 图4
经了解,不少考生对于截面的概念模糊不清,错误地认为截面就是平面,只要能找到截面上的三个不共线的点,那么这三个点确定的三角形就是截面.事实上,截面是指平面与几何体的面相交所围成的平面图形.所以截面的每条边均在几何体的表面,而图2中C1N在几何体内部,从而截面不是△C1MN.
错解2 如图3,设AB,BB1中点分别为N,D,连结MN,ND,DC1,则截面为四边形C1MND.
错解3 如图4,设AB,BC中点分别为N,D,连结MN,ND,DC1,则截面为四边形C1MND.
有的考生凭感觉取中点D,想当然认为截面就是四边形C1MND,然而C1,M,N,D四点不共面.事实上C1M与ND是异面直线.这些考生缺少对平面的直观想象,对两条异面直线缺乏直观的判断经验.普通高中教科书数学必修第二册(A版)第131页例2告诉我们一种判断异面直线的方法:与一个平面相交的直线和这个平面内不经过交点的直线是异面直线[1].若学生能运用这个方法来判断,就可以避免犯这种错误.
2 解法探究
作几何体的截面,往往是先找到截面与几何体的三个不共线的公共点,这三点确定一个三角形,再对这个三角形进行延展.延展的基本手法是延长某条边,或者过一点作对边的平行线.其理论依据是平面的三个基本事实.若涉及平行、垂直的问题,还需要线面平行、面面平行的判定定理和性质定理,以及三垂线定理等.
本题中要作出截面,考虑从线段C1M的端点下手作直线,但可能还是不清楚如何作直线.我们可以把最终目标A1B平行截面α当作条件考虑,可以想象让A1B平行移动起来,不难发现在平面A1AB内,设AB中点为N,连结MN,则MN∥A1B,MN⊂α,A1B⊄α,从而A1B∥α,接下来再作截面.
思路1通过延长直线来延拓平面
分析1 图2中平面C1MN与平面C1CBB1有一个公共点C1,直观想象MN的延长线与平面C1CBB1相交,此交点与点C1的连线就是平面C1MN与平面C1CBB1的交线.
解法1 如图5,延长MN,B1B,设MN∩B1B=D,连结C1D,交BC于点E,连结EN得截面MNEC1.
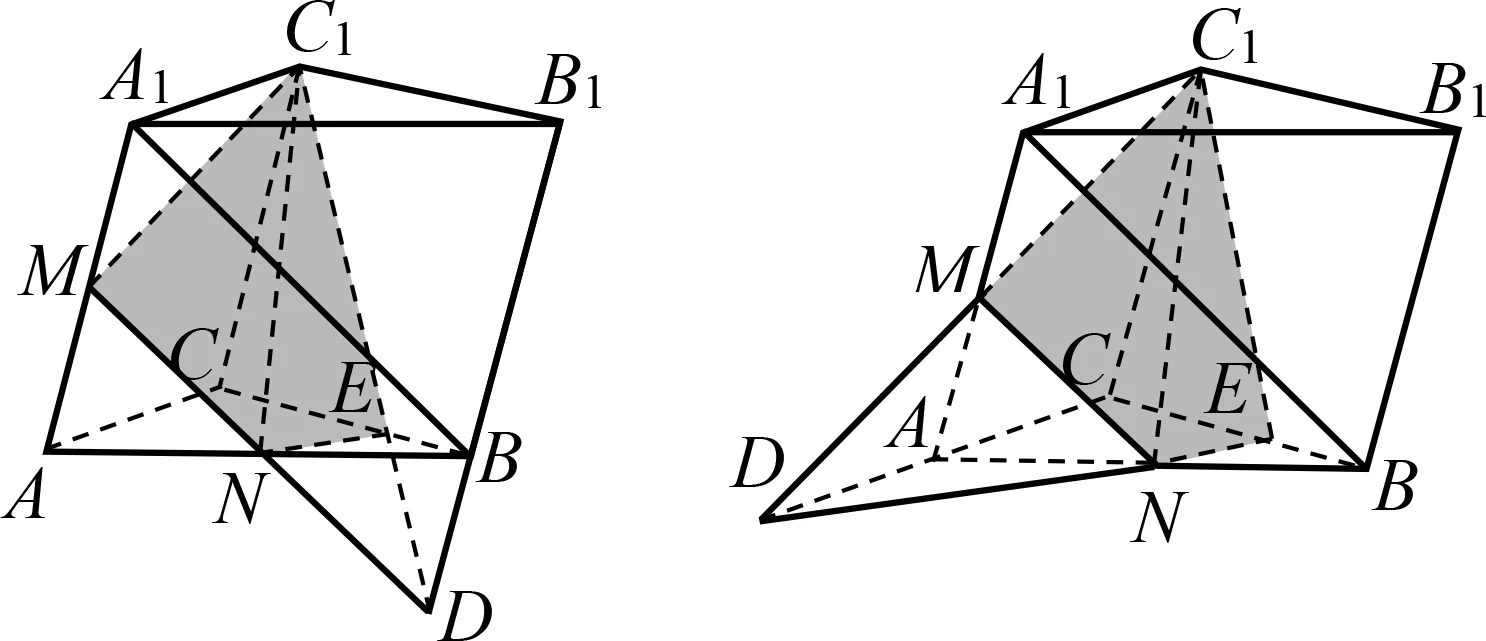
图5 图6
分析2 同分析1,考虑作平面C1MN与平面ABC的交线.
解法2 如图6,分别延长CA,C1M,设CA∩C1M=D,连结DN并延长交BC于点E,连结C1E得截面MNEC1.
思路2通过作平行直线来延拓平面.
“台州的集装箱比较分散,开辟干线的条件还尚未成熟。”周祥寿说,要让集装箱“弃陆走水”,就需要更明晰的顶层设计和更精准的服务,“就集装箱中转来说,我们争取每日开通至宁波舟山港1000—3000吨级的集装箱航班,提高台州港集装箱的喂给能力。”
分析3 要延拓△C1MN所在平面,可以从其顶点下手,作对边的平行线.基于图形的直观,尝试过点C1作MN的平行线.
解法3 如图7,过B作直线BD//AC,设BD=AC,易证BD平行且等于A1C1,则四边形A1BDC1是平行四边形,从而A1B//DC1.又MN//A1B,所以MN//C1D,那么M,N,C1,D共面.连结DN交BC于E,连结EC1得截面MNEC1.
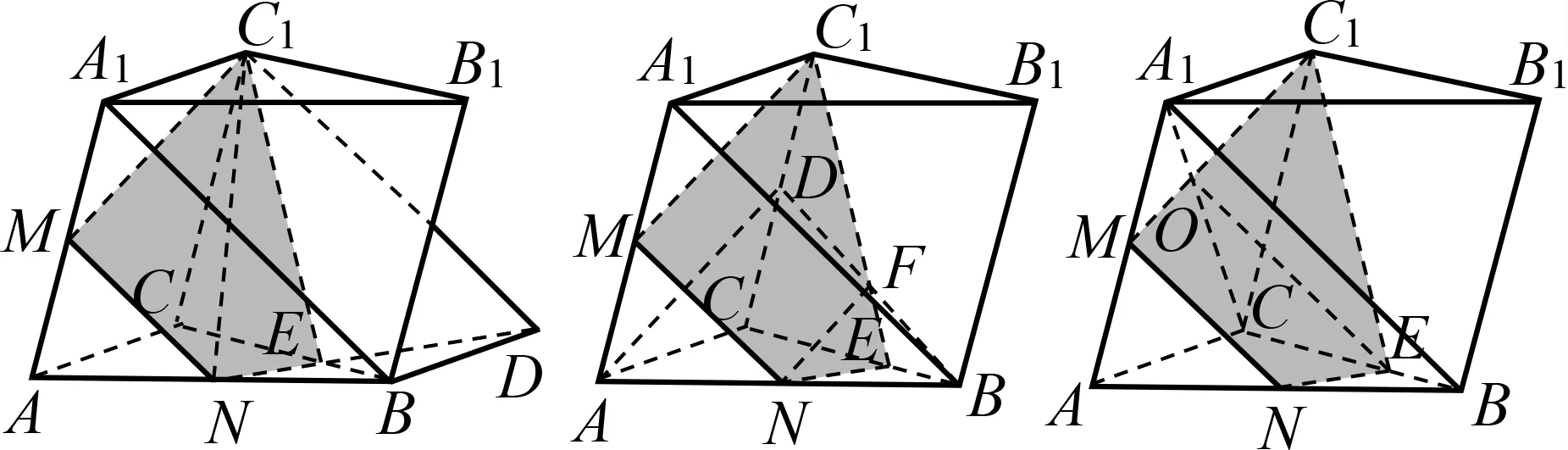
图7 图8 图9
分析4 从其顶点下手,作对边的平行线.尝试过点N作MC1的平行线,但这条平行线与平面BCC1B1的交点F不易直观确定,故考虑让MC1“落地”,即取CC1中点D,则AD//MC1,那么在△ABD中,易知点F的准确位置.
解法4 如图8,取CC1中点D,连结BD,取BD中点F,连结C1F并延长交BC于E.易证MC1//AD,AD//FN,那么MC1//FN,从而M,C1,F,N共面,连结EN得截面MNEC1.
分析5 除了直观地平移A1B至顶点M或C1,尝试平移至△C1MN内部的某个位置.考虑平面A1BC与截面必相交,则A1B平行该交线.
解法5 如图9,连结A1C,设A1C∩C1M=O,设BC∩α=E,因为A1B//α,A1B⊂平面A1BC,α∩平面A1BC=OE,则A1B//OE.易得E是线段BC的三等分点(靠近点B),连结EC1,EN得截面MNEC1.
分析6 由于上下底面平行,故截面与它们的交线必平行,这样可轻松作出交线C1D和EN确定截面.
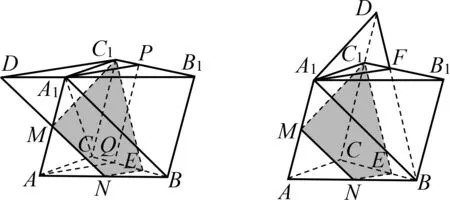
图10 图11
分析7 平面C1MN可转化为面面平行,容易想到过A1作直线平行于C1M.再利用平行平面被第三个面截得的交线平行,进而延拓平面C1MN.
解法7 如图11,延长CC1至D,使得C1D=A1M,易证A1D//C1M,又A1B//MN,从而平面C1MN//平面A1BD,则平面C1CBB1与它们的交线平行,设截面与BC交于点E,那么C1E//BF,易知E为CB的三等分点(靠近点B).连结EC1,EN得截面MNEC1.
思路3向量法
分析8 文[2]基于平面、空间向量基本定理,用向量法轻松作出截面图,令人拍案叫绝,故尝试之.
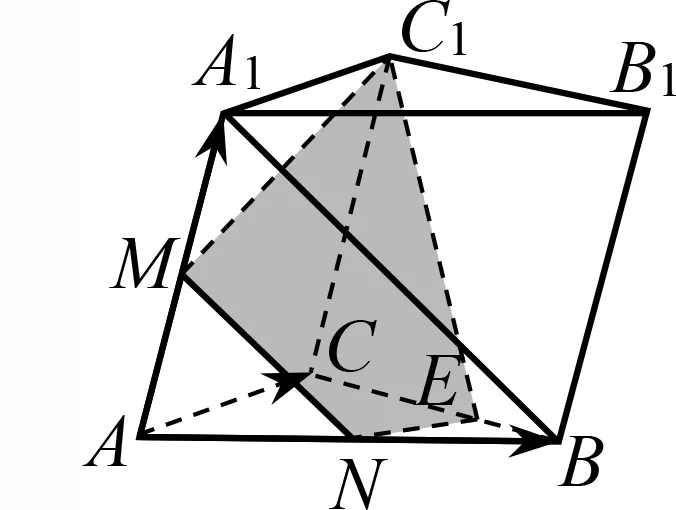
图12
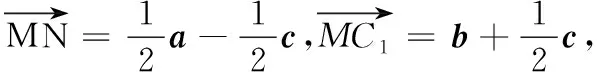
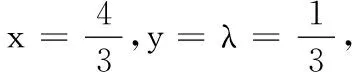
3 追根溯源
从上面的求解过程我们可以发现,学生对截面问题的思考必须经历识图、想图到构图的过程,要通过观察、分析、想象、推理、计算才能加以求解.这是立体几何教学所要求的核心素养,能很好地体现新课程背景下要求学生自主探究的理念.课程标准为帮助教师更好地理解数学学科核心素养与内容、教学、评价、考试命题的关系,提供了一些范例,其中的案例11便是一个有关截面的问题——《正方体截面的探究》,结合正方体的截面设计问题串引导学生分类找出所有可能的截面、研究截面的形状、获取截面的方法、画出截面的示意图、研究截面面积最大的三角形等.在全国卷高考试题命制中也有所体现,如2016年理科卷I题11、2018年理科卷I题12(具体试题见下方)都是有关正方体截面的问题,试题难度较大,对学生空间思维能力要求比较高;2015年理科卷II题19是有关长方体截面的问题,要求学生敢于试验、敢于探究,当判断错误时能改进试验,试题的设计突出了操作与实践性.
(2016年新课标Ⅰ卷理科第11题)平面α过正方体ABCD-A1B1C1D1的顶点A,α//平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为( ).
(2018年新课标Ⅰ卷理科第12题)已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为( ).
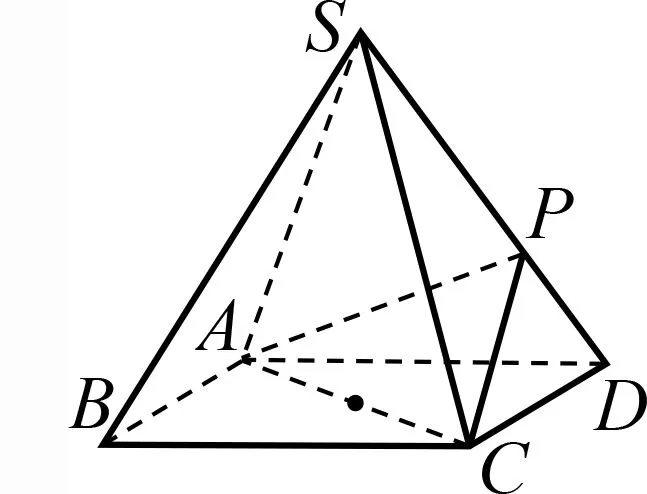
图13
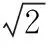
以上三道真题直接或间接地考查作截面图形的问题,图形直观、条件简洁、解法多样,值得细品.前两道选择题以正方体为载体,以面面平行为条件,考查作交线及截面问题.学生能比较熟练地作出图形,可直接作平面进而得交线,也可以转化,或不作出交线.当然亦可不作图,建立空间直角坐标系坐标化求解交线的方向向量,进而用向量夹角表示空间角.第三道解答题以线面平行为条件,可利用向量转化为数量积运算问题,也可以转化为面面平行,先作出平面再确定直线.
人教版教材第140页例题4和第171页12题分别给出了我们熟知的正方体中的面面平行与线面垂直.“直线与平面平行”一节中第138页上的例题3木料画线问题本质上也是一个截面问题.
(第140页例题4)如图14,已知正方体ABCD-A1B1C1D1,求证:平面AB1D1//平面BC1D.[1]
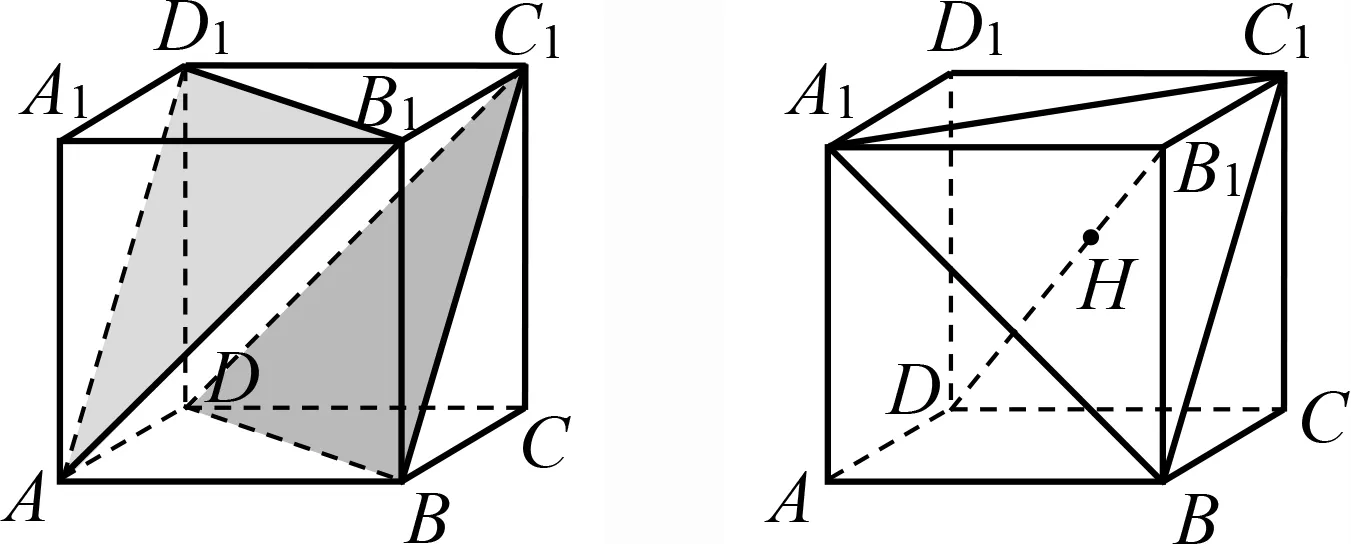
图14 图15
(第171页第12题)如图15,在正方体ABCD-A1B1C1D1中,求证:(1)B1D⊥平面A1BC1;(2)B1D与平面A1BC1的交点H是△A1BC1的重心.[1]
我们不难发现,上面的几道高考题源于教材并高于教材,题在书外、根在书内.立体几何中的作截面图形问题,往往需要先直观想象图形的结构,分析其特征,再几何论证或者代数运算,以充分发展学生的直观想象、数学运算和逻辑推理等素养.我们要坚持让学生多动手,重视画图,学会转化,引导其思考并提出问题,感悟数学思想,积累数学经验,形成和发展数学素养.

