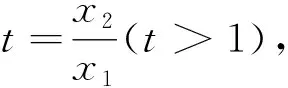极值点偏移问题的常见解法
——以2021年高考数学新高考I卷第22题为例
宗欣妍 (苏州大学数学科学学院2019级基地班 215006)
极值点偏移问题以导数为背景,考查学生运用函数与方程、数形结合、转化与化归等思想解决问题的能力.此类问题呈现形式往往比较简洁,涉及函数的双零点,是多元函数问题.
1 极值点偏移的概念
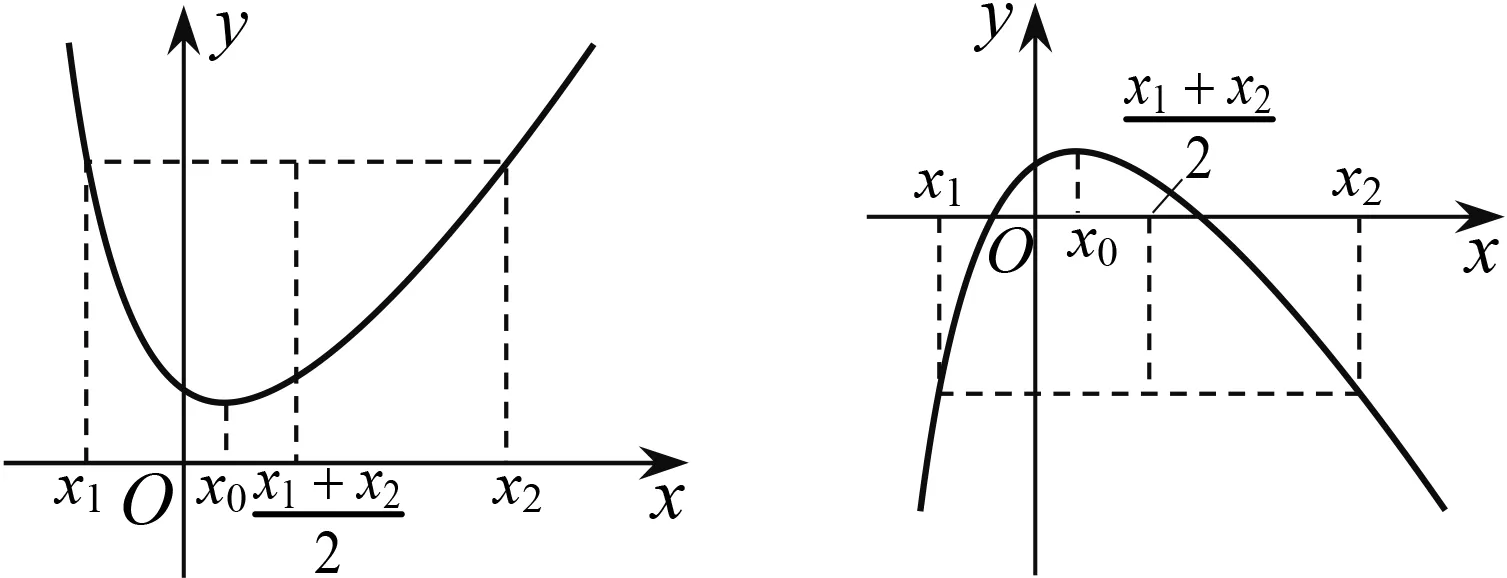
图1 图2
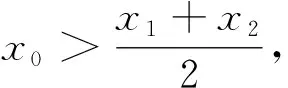
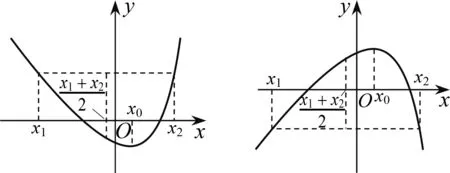
图3 图4
2 原题再现
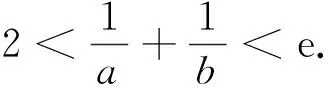
此题以基本初等函数为背景,主要考查了函数的单调性、利用导数证明不等式,考查了函数与方程、数形结合、转化与化归等思想方法,并突出考查了学生分析问题和解决问题的能力.
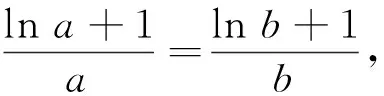
3 方法剖析
3.1 构造极值对称差函数
函数f(x)的极值点为x0,若f(x1)=f(x2),要证x1+x2>2x0(或x1+x2<2x0),往往构造对称差函数F(x)=f(x)-f(2x0-x)(x 点评构造对称差函数是极值点偏移问题的一种通性解法,主要用来解决两数和或者积与极值点相关的不等式证明问题.本题求证的不等式中含有两个变量,对于此类问题一般的求解思路是将两个变量分到不等式的两侧,然后根据函数的单调性,通过两个变量之间的关系“减元”,建立新函数,最终将问题转化为函数的单调性来求解. 事实上,有关极值点偏移的问题在高中阶段大多与指对数函数相关,而双变量的不等关系自然也可以捆绑借助对数平均不等式链来解决. 这里要说明的是,对数不等式在考场上并不能直接使用,用必证之(证明见文[1]). 点评应用对数平均不等式链来证明双变量不等式,思路简捷、别具新意、易于理解和掌握,在证明解答题时要“先证后用”.对数平均不等式的运用是近几年数学竞赛、高考数学命题的理论背景,它包含多个不等式,为我们提供了多种巧妙放缩的途径,我们可以根据证明的需要合理选取其中一个来达到不等式证明的目的. 原题的右边需证明x1+x2 方法1 根据f(x1)=f(x2),即x1(1- lnx1)=x2(1-lnx2),且0 所以φ(t)在(1,+∞)上单调递减,故t>1时,φ(t)=(t-1)ln(1+t)-tlnt<φ(1)=0,即得证x1+x2 点评上述两种解答都充分体现了数学核心素养对解题的思路引领.两种解法分别建立了对应的数学模型,通过逐步深入的逻辑推理和数据分析、数学运算简化问题,最后使问题得以轻松解决.放缩法是证明不等式的常用方法,方法1利用不等式性质放缩,方法2利用对数切线不等式lnx≤x-1进行有目标的放缩,能达到事半功倍的效果.其中利用比(差)值代换是解决极值点偏移的另一种简单快捷的方法,利用两数之比(差)作为变量t,继而将所求解问题转化为关于t的函数问题求解,将双变量问题转化为单变量问题,从而实现消元的目的. 极值点偏移问题在全国高考中属于高频题型,此类问题由浅入深,对计算难度、思维深度的要求逐步提高,很好地体现了数学的科学性、应用性和创造性.解决这类问题,本质上就是将双变量问题转化为单变量问题,建立相应的数学模型,通过逐步深入的逻辑推理和数据分析、数学运算简化问题,最后使问题得以轻松解决.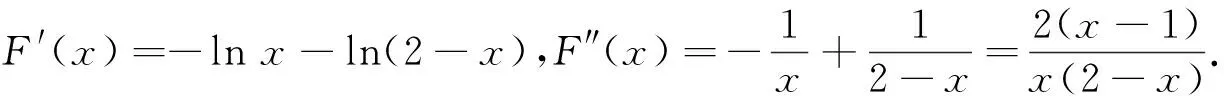
3.2 利用对数平均不等式
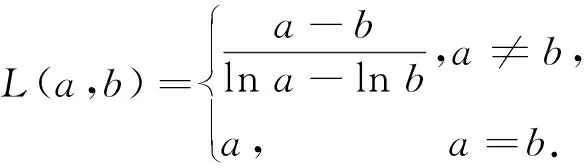
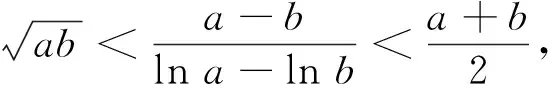
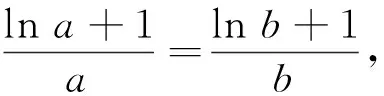
3.3 消元构造一元函数