初中生感知到的同伴支持与数学学习投入—基于变量为中心和个体为中心的分析 *

李嘉欣 雒瑞帆 封洪敏 司继伟

(山东师范大学心理学院，济南 250358)

1 引言

很多学生认为数学是最具挑战性的学科，而学生的学习投入程度是造成数学学习困难的重要原因之一（周琰, 谭顶良, 2010）。数学学习投入（mathematics learning engagement）描述了学生在学习数学时的行为表现、情感质量以及认知策略的使用情况（Fredricks et al., 2004），它能衡量个体数学学习质量的优劣并预测个体的学业成就。有研究表明，学生的数学学习投入从小学到初中存在下降趋势（Martin et al., 2015），因此系统探究初中阶段学生数学学习投入的制约因素具有重要现实意义。

学习投入的综合发展模型指出，学习投入是个体因素和环境因素相互作用的复杂过程（Wang et al., 2019），来自家庭、教师和同伴的自主性支持作为重要环境变量会显著影响学生的学习投入（柴晓运, 龚少英, 2015）。对于初中生而言，随着社交范围的不断扩大，同伴支持的重要性逐渐增大。同伴支持（peer support）是指青少年与同龄人互动时感受到情感上的关心、陪伴与帮助（Wentzel et al., 2010）。Wentzel（1998）发现，能够感知到同伴支持的学生拥有更强的心理安全感，在学业中的投入也更多。以往研究已初步证实了同伴关系在中学生数学学习中的重要作用（庄鸿娟 等,2016; Li et al., 2020）。因此本研究提出假设1：初中生感知到的同伴支持可以预测个体的数学学习投入。

在数学教育中，认同是一个非常重要的概念。关于数学认同（mathematics identity），研究者已从叙事、归属感等多个角度对其下定义，但目前尚无一致认识（Graven & Heyd-Metzuyanim,2019）。本研究参考Cribbs 等人（2015）的研究，将数学认同定义为“学生如何根据自己对数学的认知和日常经验来看待自己与数学的关系”。对前人文献的回顾表明，大多数研究者（76%）使用访谈资料来考察个体的数学认同（Graven & Heyd-Metzuyanim, 2019）。Kaspersen 和Ytterhaug（2020）修订的中学生数学认同量表为本研究提供了有效的测量工具。此外，个体的数学认同与所处的文化情境密切相关（Fernandez et al., 2022; Gonzalez et al.,2020; Miller & Wang, 2019），因此在我国背景下考察初中生的数学认同很有必要。

在同伴支持与数学学习投入的关系中，数学认同很可能是一个重要的制约因素。Cribbs 等人（2015）的解释模型指出，认知即他人对自己是否是一个数学的参与者和实践者的看法具有数学认同的最大解释率。在初中群体中，来自同伴的支持和认可有助于个体积极地看待自己与数学的关系，促进个体的数学认同（Gweshe & Brodie,2019）。此外，在诸多研究中，认同都被视为具有强大的动机成分，它会使学生趋近（或避免）认同可以被加强的情况，国外研究初步表明，数学认同是学生表现和毅力的关键因素，拥有更高数学认同水平的个体倾向于表现出更强的学习动机，在数学上有更高水平的表现（Bohrnstedt et al., 2021; Gonzalez et al., 2020; Schachter & Rich,2011）。但目前同伴支持、数学认同和数学学习投入三者之间的作用机制尚不明晰。基于前人相关理论认识与实证证据，本研究提出假设2：同伴支持可能增强个体的数学认同，从而间接影响数学学习投入。

此外，数学焦虑也可能作为同伴支持影响个体数学学习投入时的一个重要中介因素。数学焦虑（math anxiety）是个体在解决与数学相关的问题时产生的不安、紧张等焦虑状态（耿柳娜, 陈英和,2005）。它会占据个体的工作记忆资源并影响认知策略的使用，进而降低个体学习投入程度，已有研究证实了数学焦虑对数学学习投入的负向预测作用（屠西茜, 杨新荣, 2021）。根据Pekrun（2006）的学业情绪控制-价值理论，当个体对情境持有适度的控制感且关注失败时，容易产生焦虑情绪，而环境因素如自主性支持是学业情绪的重要影响因素。作为学生发展的重要环境变量，同伴支持能够作为保护性因素帮助个体降低焦虑等消极情绪（Monteiro et al., 2017）。基于以上分析，本研究提出假设3：同伴支持可以通过降低个体的数学焦虑水平从而间接影响数学学习投入。

此外，数学认同和数学焦虑之间也可能存在一定联系。数学认同的解释模型指出（Cribbs et al.,2015），数学认同有认知和兴趣两个子成分，而这两个成分与数学焦虑有密切的联系。已有研究证实了数学兴趣和数学焦虑之间的负相关关系（吴甲旺 等, 2022），研究也发现学生如何感知他人在数学方面对自己的看法影响学生对自己能力的感知与学业表现（Bohrnstedt et al., 2021），而后者是数学焦虑的重要影响因素（Du et al., 2021; Sorvo et al.,2019）。Fernandez 等人（2022）指出，更高的数学认同可能会减轻女生的焦虑情绪。因此，本研究提出假设4：数学认同和数学焦虑可能在个体感知到的同伴支持与数学学习投入的关系中存在链式中介作用。

前人对数学学习投入的研究多从变量为中心的角度开展，但以变量为中心的分析方法关注的是样本平均水平，群体内部的异质性容易被忽略。本研究将进一步采用以个体为中心的思路，探讨不同个体因素（认同和焦虑）在个体身上究竟如何组合，以了解同伴支持对不同类型学生的预测作用和不同类型学生在数学学习投入上存在的差异。

潜剖面分析（latent profile analysis, LPA）是一种新兴的以个体为中心的研究方法，国内外学者已开始运用此方法开展研究。例如，贾莹（2021）运用潜剖面分析探讨了家庭因素对学业投入类型的影响，司继伟等人（2022）采用该方法考察小学儿童数学焦虑的不同类别，这为本研究探讨个体焦虑与认同的不同组合模式提供了现实可能。Luttenberger 等人（2018）在数学焦虑框架中指出数学焦虑与动机因素（如数学认同）存在交互作用，换言之，不同个体之间在数学焦虑与数学认同上可能存在不同程度的组合，而这对数学学习投入或许产生不同的预测作用。鉴于相关的支持性文献还比较罕见，对此仅进行探索性研究，并提出假设5：认同和焦虑在不同个体身上存在不同组合类型，同伴支持可显著预测不同亚组，不同类型个体之间的数学学习投入水平存在明显差异。

综上，本研究旨在我国文化背景下，采用变量中心和个体中心结合的方法，探究初中生感知到的同伴支持、数学认同、数学焦虑与数学学习投入的关系，并进一步探讨不同类型学生的数学学习投入特点，为促进学生的学习投入提供证据支持。

2 研究方法

2.1 被试

选取山东省济南市两所中学七、八年级的学生共1268 人作为被试，剔除无效问卷91 份，有效问卷1177 份，有效率92.82%。其中男生618 人，女生559 人，平均年龄12.89±0.74 岁，七年级602人，八年级575 人。本研究涉及的所有工具和流程获得山东师范大学伦理委员会认可。调查结束后所有参与者均获得一份精美小礼物。

2.2 研究工具

2.2.1 领悟社会支持量表

采用由Zimet 等人（1988）编制，后经黄丽等人（1996）修订的领悟社会支持量表，包括家庭支持、同伴支持以及其他支持3 个维度。本研究选用其中的同伴支持分量表，共4 个项目，采用7 点计分，1 表示“非常不同意”，7 表示“非常同意”，得分越高，表示个体感知到的同伴支持越高。为符合研究目的，借鉴庄鸿娟等人（2016）的做法，将原量表中一般情境下的同伴支持改为同伴在数学学习中给予的支持。本研究中该量表的验证性因子分析主要拟合指标为：χ2/df=3.85，RMSEA=0.05，CFI=0.99，TLI=0.99，SRMR=0.01，内部一致性系数为0.86。

2.2.2 中学生数学认同量表

该量表改编自由Kaspersen 和Ytterhaug（2020）修订的中学生数学认同量表。该量表包括20 个项目，采用4 点计分，1 表示“从不”，4 表示“总是”，得分越高，表示个体的数学认同水平越高。本研究按照标准流程对量表进行本土化修订，经项目分析和探索性因素分析删去4 个项目，保留单一维度，共16 个项目，本研究中该量表的验证性因子分析主要拟合指标为：χ2/df=3.77，RMSEA=0.07，CFI=0.93，TLI=0.92，SRMR=0.04，内部一致性系数为0.92，分半信度系数为0.91，重测信度系数为0.70，表明量表具有良好的信效度，等值性检验表明，修订后的量表具有跨性别和年级的等值性。

2.2.3 数学焦虑量表

采用张晓龙（2004）修订的适合初中生的数学焦虑量表，包括数学课堂焦虑、数学个人焦虑、数学考试焦虑3 个维度。量表采用5 点计分，1 表示“没有焦虑”，5 表示“非常焦虑”，得分越高，表示个体的数学焦虑水平越高。本研究中该量表的验证性因子分析主要拟合指标为：χ2/df=6.29，RMSEA=0.07，CFI=0.94，TLI=0.93，SRMR=0.05，内部一致性系数为0.95。

2.2.4 中学生数学学习投入量表

采用柴晓运和龚少英（2015）编制的数学学习投入量表，包括认知投入、情感投入和行为投入3 个维度，共13 个项目。量表采用5 点计分，1 表示“完全不符合”，5 表示“完全符合”，得分越高，表示个体的数学学习投入水平越高。本研究中该量表的验证性因子分析主要拟合指标为：χ2/df=6.81，RMSEA=0.07，CFI=0.96，TLI=0.95，SRMR=0.03，内部一致性系数为0.92。

2.3 研究程序和数据处理

以班级为单位进行集体施测，被试独立填写问卷。运用SPSS19.0 对数据进行清理、预处理以及描述性统计分析，运用Mplus7.0 对数据进行结构方程模型分析以及潜剖面分析。

3 结果

3.1 共同方法偏差检验

采用Harman 单因素因子分析来检验数据的共同方法偏差，结果显示未旋转的因子分析得到6 个因子，第一个因子解释方差变异为35.14%，小于40% 的标准，表示不存在严重的共同方法偏差（汤丹丹, 温忠麟, 2020）。

3.2 描述性统计和相关分析

各变量的描述统计及相关分析结果如表1 所示。数学焦虑与同伴支持、数学认同和数学学习投入均呈显著负相关（ps＜0.001），同伴支持、数学认同和数学学习投入之间均存在显著正相关（ps＜0.001）。此外，数学学习投入存在显著的年级差异，七年级学生的数学学习投入显著高于八年级学生（t=2.37,p＜0.05）。数学认同、数学焦虑和数学学习投入存在显著性别差异，男生的数学认同显著高于女生（t=4.52,p＜0.001），男生的数学焦虑显著低于女生（t=-6.31,p＜0.001），男生的数学学习投入显著高于女生（t=3.26,p＜0.01）。

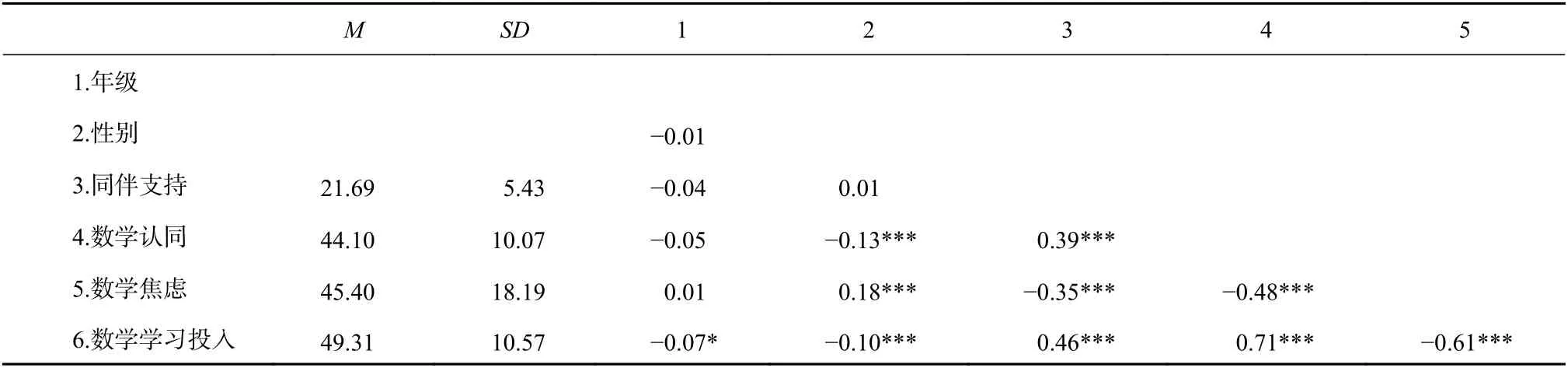
表1 同伴支持、数学认同、数学焦虑和数学学习投入的描述统计及相关分析（n=1177）

3.3 初中生感知到的同伴支持、数学认同、数学焦虑和数学学习投入的关系模型

由于数学认同量表有16 个项目，为防止项目过多引起误差膨胀，采用单因子法进行打包处理（吴艳, 温忠麟, 2011)，将项目打包成三个小组，纳入结构方程分析。以感知到的同伴支持为预测变量，数学学习投入为结果变量，数学认同和数学焦虑为中介变量建立潜变量模型，将性别和年级作为协变量也纳入模型中（见图1）。结果显示，该模型的拟合指数为：χ2/df=7.70，CFI=0.97，TLI=0.95，RMSEA=0.07，SRMR=0.04，说明该模型拟合良好。结果发现，同伴支持显著正向预测数学认同（β=0.41,p＜0.001）和数学学习投入（β=0.12,p＜0.001）；数学认同显著正向预测数学学习投入（β=0.54,p＜0.001）；同伴支持（β=-0.17,p＜0.001）和数学认同（β=-0.44,p＜0.001）显著负向预测数学焦虑；数学焦虑显著负向预测数学学习投入（β=-0.32,p＜0.001）。

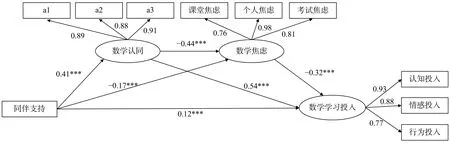
图1 初中生感知到的同伴支持、数学认同、数学焦虑和数学学习投入的关系模型图

采用Bootstrap 分析方法检验中介效应是否显著，重复取样2000 次，置信区间设定为95%，从同伴支持到数学学习投入的链式中介路径的置信区间为[0.04, 0.07]，不包括0，表明链式中介效应显著。各中介路径的效应值如表2 所示，表明学生感知到的同伴支持不仅直接作用于数学学习投入，还可以通过数学认同经数学焦虑间接影响数学学习投入。为检验中介模型的性别差异，分别在未经限定（M1）、限定测量权重相等（M2）、限定测量和结构权重相等（M3）的情况下，自由估计模型，结果显示M1 与M2 之间不存在显著差异（Δχ2=6.07, Δdf=5,p＞0.05），M2 与M3 之间也不存在显著差异（Δχ2=7.65, Δdf=6,p＞0.05），表明该模型具有性别等同性。

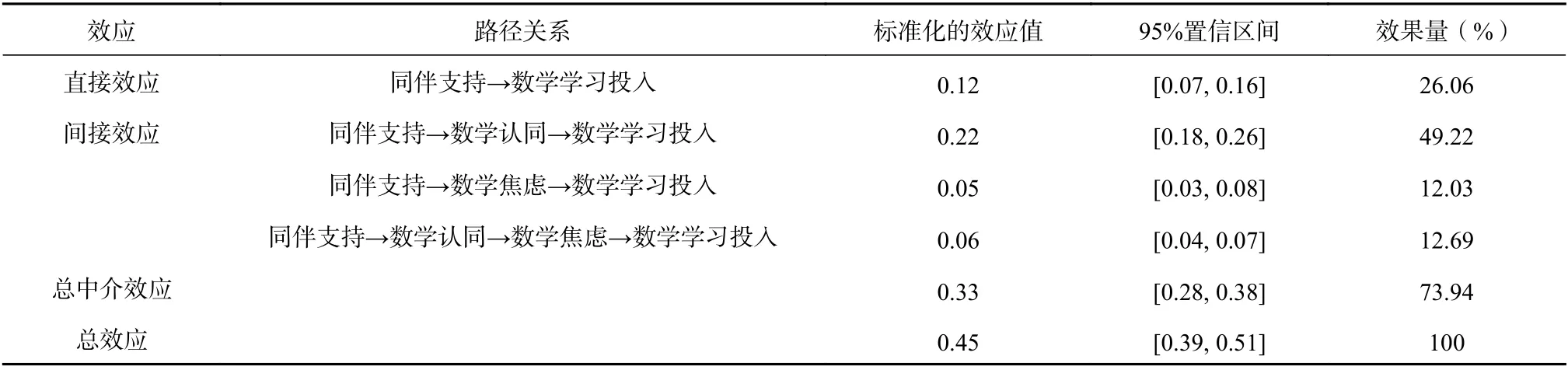
表2 初中生感知到的同伴支持和数学学习投入中介模型路径分析

3.4 数学认同和数学焦虑的潜在类别：以个体为中心

为进一步探讨同伴支持对不同类型学生的预测作用及他们表现出的数学学习投入之间的差异，以数学认同和数学焦虑各维度得分为指标，将学生类型依次设置为1 类，2 类，3 类和4 类进行潜剖面分析，模型拟合结果参见表3。由于分成4 类时，虽然LMRT 达到显著，各项指标有所提升，但其中一个类别占比仅为2%，故采用三类别模型。根据数学认同水平和数学焦虑水平方面的特点，将所得三个类别分别命名为高认同-低焦虑型、中认同-中焦虑型、低认同-高焦虑型（见图2）。

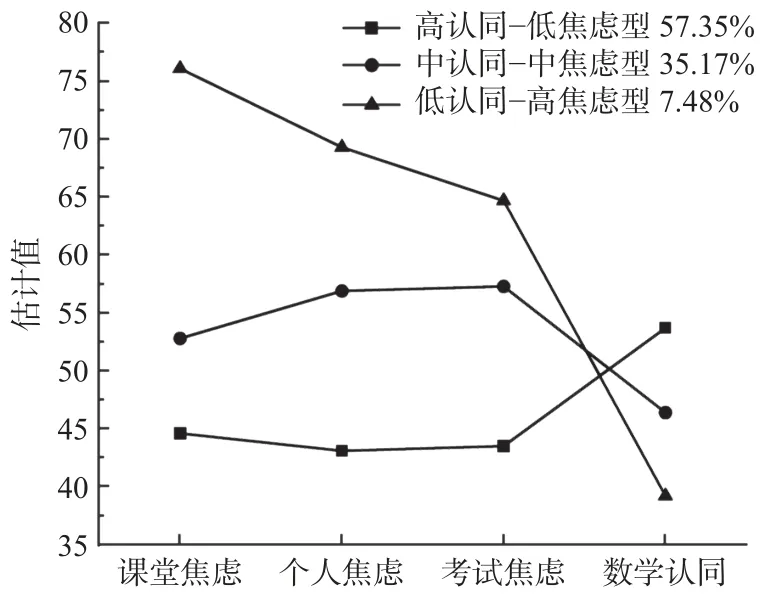
图2 数学认同与数学焦虑潜在类别

表3 不同数学认同和数学焦虑类型的潜在剖面拟合分析

基于上述潜在剖面分析的结果，进一步探究同伴支持对不同类型学生的预测性及不同类型学生在数学学习投入水平上的差异。以潜在剖面的分类结果作为因变量，同伴支持作为自变量进行多元Logistic 回归，并把类别“低认同-高焦虑型”作为比较参考类别。结果表明，同伴支持显著影响初中生认同-焦虑不同类型的分布，相对于低认同-高焦虑组而言，个体感知到的同伴支持越高，则越可能归属于高认同-低焦虑组（OR=1.23,p＜0.001）和中认同-中焦虑组（OR=1.13,p＜0.001）。此外，不同类型组合学生的数学学习投入得分差异显著，F(2, 1174)=281.68，p＜0.001。多重比较结果显示，高认同-低焦虑组的数学学习投入得分（53.91±8.67）要显著高于其他两组，中认同-中焦虑组的数学学习投入得分（45.10±8.29）显著高于低认同-高焦虑组（33.86±10.62）。

4 讨论

4.1 同伴支持对数学学习投入的预测

根据研究结果，同伴支持能正向预测初中生的数学学习投入，这与以往研究结果一致（燕良轼 等, 2018）。自我决定理论（self-determination theory, SDT）对此能做出很好的解释（Deci &Ryan, 2000）。在数学学习中，同伴可以为学生提供实质性支持（如讲解数学难题）和情感支持（如给予安全感），这可以满足青少年的关系需要，后者作为人类的基本需要之一，又具有动力特性，当它得到满足时，学生更可能投入到数学学习中去（Furrer & Skinner, 2003）。

4.2 数学认同和数学焦虑的中介作用

本研究通过修订量表，在本土文化背景下考察了初中生的数学认同，整体而言初中生对数学的认同感较高（M=44.10）。此外，本研究结果支持了假设2，即数学认同在同伴支持和数学学习投入之间存在中介作用。根据社会学习理论，学生感知到的同伴支持越高，则越相信自己在同伴眼中是数学学习的参与者，对数学产生强烈的认同感（Cribbs et al., 2015），产生积极的学习动机和学习主动性，这会使他们面对学习困难时更加坚持，愿意花费更多的时间参与学习活动，通过理解学习内容提升自身认知策略，进而促进数学学习投入（张勇强, 杨新荣, 2022; Miller & Wang, 2019;Ryan & Deci, 2020）。

此外，本研究结果也支持了假设3，即数学焦虑在同伴支持和数学学习投入之间存在中介作用，这与以往研究结果一致（洪伟 等, 2018; 屠西茜, 杨新荣, 2021）。干扰理论模型指出，数学焦虑个体面临数学情境时，会出现各种思维如担忧和消极的自我集中（Mandle & Sarason, 1952），而当个体感受到同伴给予的鼓励和帮助时，他们会减少这种消极思维，以更积极的情绪投入到数学学习中。该结果也支持了学业情绪的控制-价值理论，表明同伴的自主支持和合作的学习环境有利于增强学生的能力感和控制感，减少其焦虑情绪，获得更多关于数学的积极体验，从而对数学学习投入产生促进作用（Pekrun, 2006; Wang et al.,2021）。

另外一个重要发现是，数学认同和数学焦虑在同伴支持和数学学习投入的关系中具有链式中介作用，这一结果支持了假设4。当学生感知到来自同伴对自己数学学习的支持时，会激发他们对数学的认同感，认同感的增强会伴随着数学学习兴趣的增强以及对自己能力的积极感知（Cribbs et al.,2015），这些会增加学生对数学学习稳定的心向，有更好的成绩表现，降低由不良表现带来的焦虑情绪，增加学习时的积极情感体验，进一步投入到数学学习中去（吴甲旺 等, 2022; Sorvo et al., 2019）。

4.3 不同认同-焦虑类型学生在数学学习投入上的差异

本研究基于个体为中心的潜在剖面分析方法探索初中阶段学生可能存在的数学认同与数学焦虑的不同类别组合，在综合考虑拟合指标和分类实际意义的基础上，确定了三种剖面类型：数学认同水平高、数学焦虑水平低的学生，即高认同-低焦虑型，占总人数的57.35%；数学认同和数学焦虑水平都适中的学生，即中认同-中焦虑型，占总人数的35.17%；数学认同水平低、数学焦虑水平高的学生，即低认同-高焦虑型，占总人数的7.48%。上述分类为进一步理解学生数学学习投入的影响因素提供了新的证据支持。

结果表明，大多数初中生对数学持有较高的认同感，同时伴随较低的数学焦虑水平；仅有少数学生对数学持有较低的认同感和较高的焦虑水平，而且在数学焦虑的三个维度上，课堂焦虑水平最高，这可能源于数学认同与数学课堂情景之间的密切联系（Langer-Osuna, 2017）。此外，感知到的同伴支持会显著影响学生类型的分布情况，高同伴支持有利于个体形成对数学的积极认同和低焦虑状态；与其他类型学生相比，高认同-低焦虑的学生在数学学习投入上也更多，这就进一步验证了前面以变量为中心的研究结果，强调了数学认同和数学焦虑在同伴支持和数学学习投入中的重要作用。这既支持了学习投入的综合发展模型（Wang et al., 2019），表明了数学学习投入的环境因素与个体因素的交互作用机制，也支持了认知-情感-行为理论（Ellis & Dryden, 1997），即数学认同高的个体，会对数学产生积极的情感联结，伴随更多的积极情绪，有更多的学习投入。

4.4 研究的意义和局限

本研究扩展了数学学习投入研究领域，深入探讨了初中生感知到的同伴支持、数学认同、数学焦虑以及数学学习投入之间的作用机制，同时探讨了学生所具有的认同-焦虑的潜在类别、同伴支持对不同类别学生的预测性以及不同类别学生在数学学习投入上的差异，对于数学教育实践工作具有重要现实指导意义：面对学生进入初中后其数学学习投入存在的下降趋势，教师需要营造支持性的学习氛围，激发学生对数学的积极认同感并减少数学焦虑情绪，这应是促进学生数学学习投入的一个有效途径。研究也存在一定局限性。第一，本研究属于横断研究，无法得出变量间的因果关系，未来研究可以对初中生展开纵向调查以探究各变量的动态发展变化。第二，数学认同的含义广泛，本研究主要探讨了数学认同的动机方面的作用，未来研究可考虑从更广阔的视角探究其作用机制。

5 结论

（1）初中生感知到的同伴支持不仅可以直接预测数学学习投入，也可以通过数学认同和数学焦虑的链式中介作用间接预测数学学习投入；（2）学生存在着高认同-低焦虑、中认同-中焦虑和低认同-高焦虑三种不同类型，同伴支持有利于个体形成对数学的积极认同和低焦虑状态，与其他类型学生相比，高认同-低焦虑的学生数学学习投入也更多。