平面应力状态下主应力方向的快速判定方法探讨

缪广红，卢小雨，罗吉安，吴建强

（安徽理工大学 力学与光电物理学院，安徽 淮南 232001）

0 引言

工程中关于结构设计的基本原则是解决经济和安全之间的矛盾，即既要经济合理又要安全可靠，构件在载荷的作用下是否安全可靠的工作，就需要掌握构件内各点主应力的变化规律，因此，十分有必要在构件设计之前，研究构件内危险截面上危险点的主应力大小和方向，即应力状态分析。

应力状态分析作为工程力学、材料力学、弹塑性力学等固体力学分支研究的核心内容，其中主应力方向直接影响着后续强度计算的正确性，如何正确的判断主应力方向一直是力学教学和解决工程实践中的一个重点，同时也是一个难点，对工程实际和理论教学都有着十分重要的意义，而且对学生而言，从宏观到微观、从微观到宏观的思维方法也得到了培养。一般教材[1-3]中关于平面应力状态下主应力的方向判定，只作了如下表述：若约定 |α0| ＜ 45°，即取值在α0±45°范围内，而确定主应力方向的具体规则为，①当σx＞σy时，α0确定σmax所在的主平面；② 当σx＜σy时，α0确定σmin所在的主平面；③ 当σx=σy时，α0=45°，主应力的方向可由单元体上切应力情况直观判断出来，并无十分全面的论证和描述。马云玲提出了由单元体上的正应力和切应力来判断主应力的方向[4]。刘刚等利用高等数学的极值理论探讨了主应力方向的判定方法[5]。宋志强等总结归纳了代入法、作图法和正应力比较法判定主应力的方法，并指出了各自的优缺点[6]。陶建新采用解析法和图解法判定主应力方向，并进行了比较[7]。虽然相关学者对平面应力状态下的主应力方向的判定进行了诸多研究，并提出了各自的判定方法，但在理论上还有进一步提高透明度和简化的必要。为此，本文结合已有的一些相关研究和作者的教学经验，对平面应力状态下主应力方向的断定方法作如下探讨，旨在对理论教学和工程实践中快速判定主应力的方向提供一定的参考。

1 主应力方向规定及证明

有的教材[1-3]认为，在平面应力状态下，主应力的方向可由公式（1）计算得到，

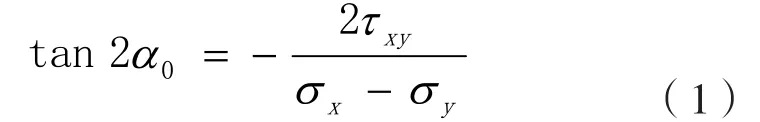
但满足式（1）的解有两个:α0和α0+90°。若约定 |α0| ＜ 45°，即α0取值在 ±45°范围内，而确定主应力方向的具体规则，教材中仅有如下描述：

规则①： 当σx＞σy时，α0确定σmax所在的主平面；

规则②：当σx＜σy时，α0确定σmin所在的主平面；

规则③：当σx=σy时，α0=45°，主应力的方向可由单元体上切应力情况直观判断出来。

鉴于上述规定在教材中无理论依据和详细的论述，下面对上述规则进行理论证明。

规则①证明：

规则①规定，当σx＞σy时，即σx-σy＞0，且 |α0| ＜ 45°，即 cos2α0＞ 0，

结合公式（1）可得：

再结合公式（1）和公式（2）可知：

将公式（2）和（3）代入下式：

整理可得，

公式（5）与σmax的表达式一致，即规则（1）得到证明。

规则②证明：

规则②规定，当σx＜σy时，即σx-σy＜0，且|α0| ＜ 45°，即 cos2α0＞ 0，

结合公式（1）可得：

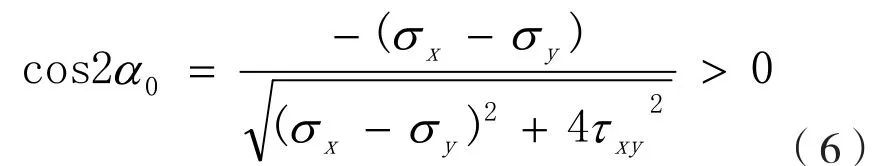
再结合公式（1）和公式（6）可知：

将公式（2）和（3）代入公式（4），整理可得，

公式（8）与σmin的表达式一致，即规则②得到证明。

2 直观判断方法

由于规则①和规则②关于主应力方向判定的文字表述过于繁琐，下面介绍一种利用单元体上切应力方向直观快速判定主应力方向的方法。

如图1所示τxy为正时的平面应力状态，当σx＞σy时，由公式（1）可知，tan2α0＜ 0，即 -45°＜α0＜ 0，对应图 2 中的α01，结果与规则①相对应；当σx＜σy时，由公式（1）可知，tan2α0＞ 0，即 0＜α0＜45°，对应图 2 中的α02，结果与规则②相对应。可见，主应力的方向与正应力的大小和方向无关，判断主方向时，可以不考虑正应力，这就相当于将原来的应力单元体分解为只有正应力和只有切应力的单元体，由只有切应力的单元体直观的判断主应力的方向。

图1 τxy为正时的平面应力状态

如图3所示τxy为负时的平面应力状态，当σx＞σy时，由公式（1）可知，an2α0＞ 0，即0＜α0＜ 45°，对应图 4中的α04，结果与规则①相对应；当σx＜σy时，由公式（1）可知，tan2α0＜ 0，即-45°＜α0＜0，对应图4中的α03，结果与规则②相对应。可见，主应力的方向与正应力的大小和方向无关，判断主方向时，可以不考虑正应力，这就相当于将原来的应力单元体分解为只有正应力和只有切应力的单元体，由只有切应力的单元体直观的判断主应力的方向。

图3 τxy为负时的平面应力状态

图4 τxy为负时主应力方向

3 讨论

例1：试求图5所示单元体主应力的大小及方向。

图5 单元体示例1

解：已知应力分量σx=80 MPa，σy= -40 MPa，τxy= -60 MPa，

由主应力计算公式[1-3]得

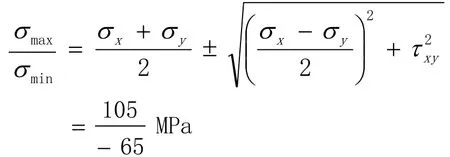
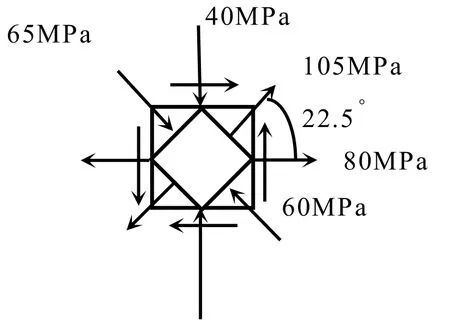
图6 单元体主方向

图6中主应力的方向是通过教材中规则①可确定主方向，采用本文第三部分提出的直观判断方法可由原单元体分解得到的仅有切应力单元体上的切应力方向直观判断，如图7所示，主方向判定结果与图6一致。

图7 单元体主方向

例2：试求图8所示单元体主应力的大小及方向。

图8 单元体示例2

解：已知应力分量σx=-20 MPa，σy= 30 MPa，τxy= 20 MPa，由主应力计算公式[1-3]得

图9 单元体主方向

图9中主应力的方向是通过教材中规则②可确定主方向，采用本文第三部分提出的直观判断方法可由原单元体分解得到的仅有切应力单元体上的切应力方向直观判断，如图10所示，主方向判定结果与图9一致。

图10 单元体主方向

4 归纳总结

通过以上的分析和证明不难发现，根据教材中的方法判定平面应力状态下的主应力方向比较繁琐，而仅通过单元体上切应力的方向判定出单元体上主应力方向更简单、更直观，有非常明显的优越性，在以后的工程实际和日常教学中可以仅利用单元体上切应力的方向快速直观地判定主应力的方向，判定方法对本科生和研究生理论教学和工程实践都有着十分重要的意义。