基于机器学习技术的混凝土抗压强度预测研究

周宜松，赵传萍，黄耀明，朱 丽，程 明

（1.信阳学院 土木工程学院，河南 信阳 464000；2.中国建筑第五工程局有限公司，长沙 410000）

混凝土是世界上最常用的建筑材料之一。在混凝土的力学性能中，抗压强度是最基本也是最重要的力学性能之一。为了通过合理的混合比达到粉煤灰混凝土的预期抗压强度，传统的方法需要不断调整混凝土的混合比来制作实验室混凝土试样，然后进行压缩试验，以获得其抗压强度。如果强度没有达到预期标准，就需要重新制作试样。这显然是一项非常耗费时间和人力的工作。如果能用一种方法在压缩试验前对给定混合料的混凝土抗压强度进行粗略估计，将大大节省试验和试样的时间和成本。

随着机器学习的出现及其在土木工程领域的发展，各种机器学习模型在预测混凝土力学性能方面得到了应用并取得了良好的效果[1-5]。李地红等[6]采用BP神经网络对混凝土的抗压强度和坍落度等综合性能进行预测，与试验值相比，预测相对误差集中在15%以内，基本满足工程实践要求。梁宁慧等[7]利用决策树、支持向量回归（SVR）和人工神经网络（ANN）三种方法预测高温后聚丙烯纤维混凝土强度，其中ANN达到了最佳的预测效果。Shamiri等[8]开发了一个极端学习机（ELM）模型来预测高强度混凝土的强度，该模型取得了较高的精度和良好的泛化能力。吴贤国等[9]采用随机森林方法（RF）预测高性能混凝土的抗压强度，结果表明所提的随机森林方法在高性能混凝土抗压强度预测方面具有良好的优势。Xu等[10]提出了一个改进的随机森林模型来预测高性能混凝土的抗压强度。结果表明，该模型的预测精度高于其他算法，而且该方法表现出很强的泛化能力。

总的来讲，机器学习模型在混凝土力学性能的预测中表现出良好的适用性。但利用随机森林来分析混凝土力学性能的研究仍是相对较少的。为了更好地理解和应用随机森林模型，需要在这个领域进行进一步探索。为此本文尝试采用随机森林模型对混凝土抗压强度进行预测，并将预测结果与传统的ELM和SVR比较。

1 试验方法

随机森林是最先进的集成算法之一，具有模型参数少、抗过拟合能力强的优点。决策树是随机森林的基本预测器。如图1所示，随机森林回归算法以决策树为基本模型，通过构建不同的训练数据集和不同的特征空间，产生一系列差异化的决策树模型，通常采用投票或平均法得到最终结果。其数学表达式为

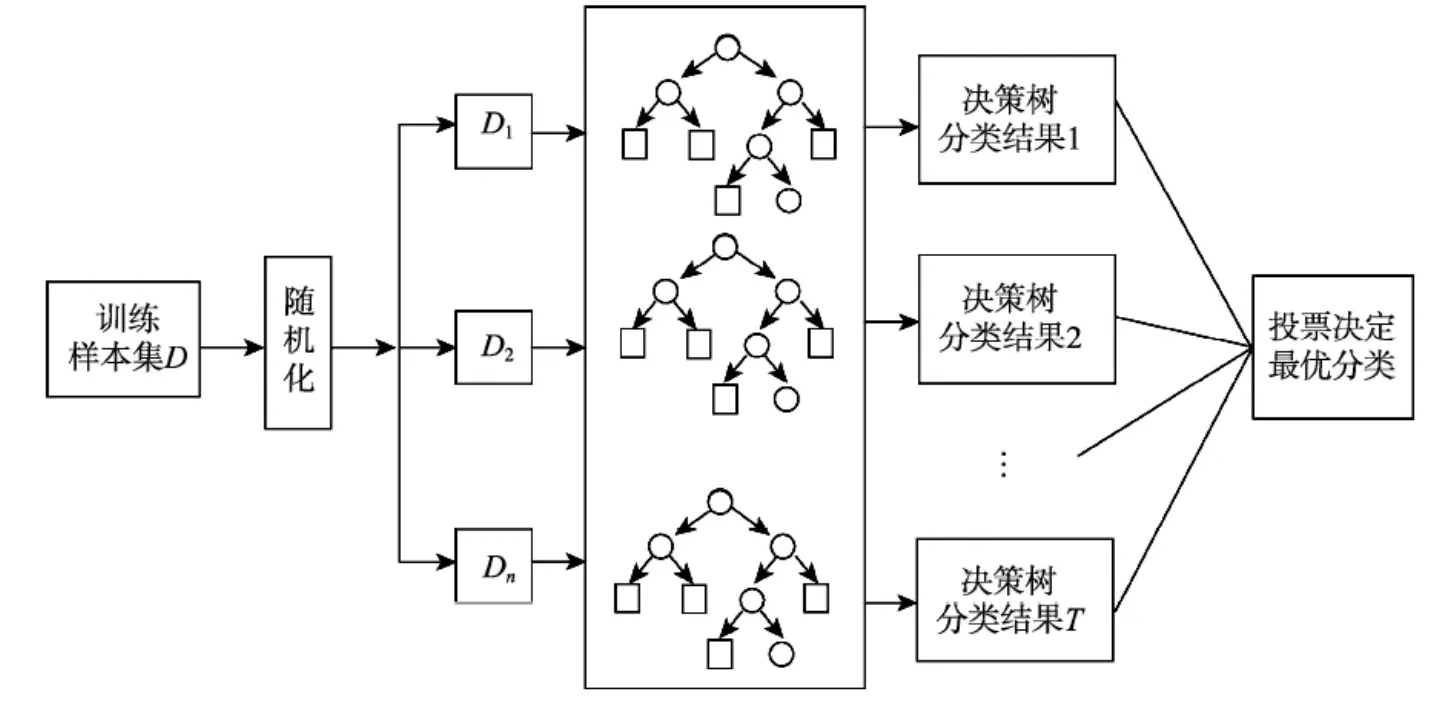
图1 随机森林模型示意图[11]

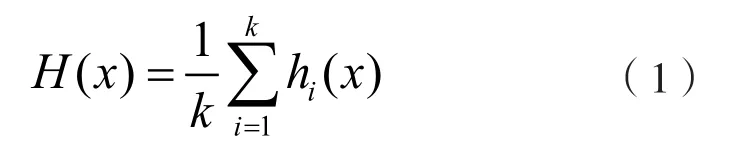
其中，H（x）表示随机森林回归模型的预测值，hi（x）表示第i个决策树模型的输出。

2 输入和输出特征

一共收集了270组数据集。这些数据包括八个输入变量和一个输出变量。这些变量分别是水泥、粉煤灰、水、减水剂、粗集料、细集料、龄期和水胶比。表1和图2显示了这些变量的统计特征和分布。这些变量的分布表明，这些变量是高度离散的，而且任意一个输入变量与输出抗压强度之间的皮尔逊系数都未超过0.8。这也从侧面说明了多个输入变量和抗压强度之间存在着复杂的非线性相关关系。本文的目的是旨在建立这种非线性的关联性。从所有的数据样本中随机选择216组数据作为训练集，其余的作为测试集。

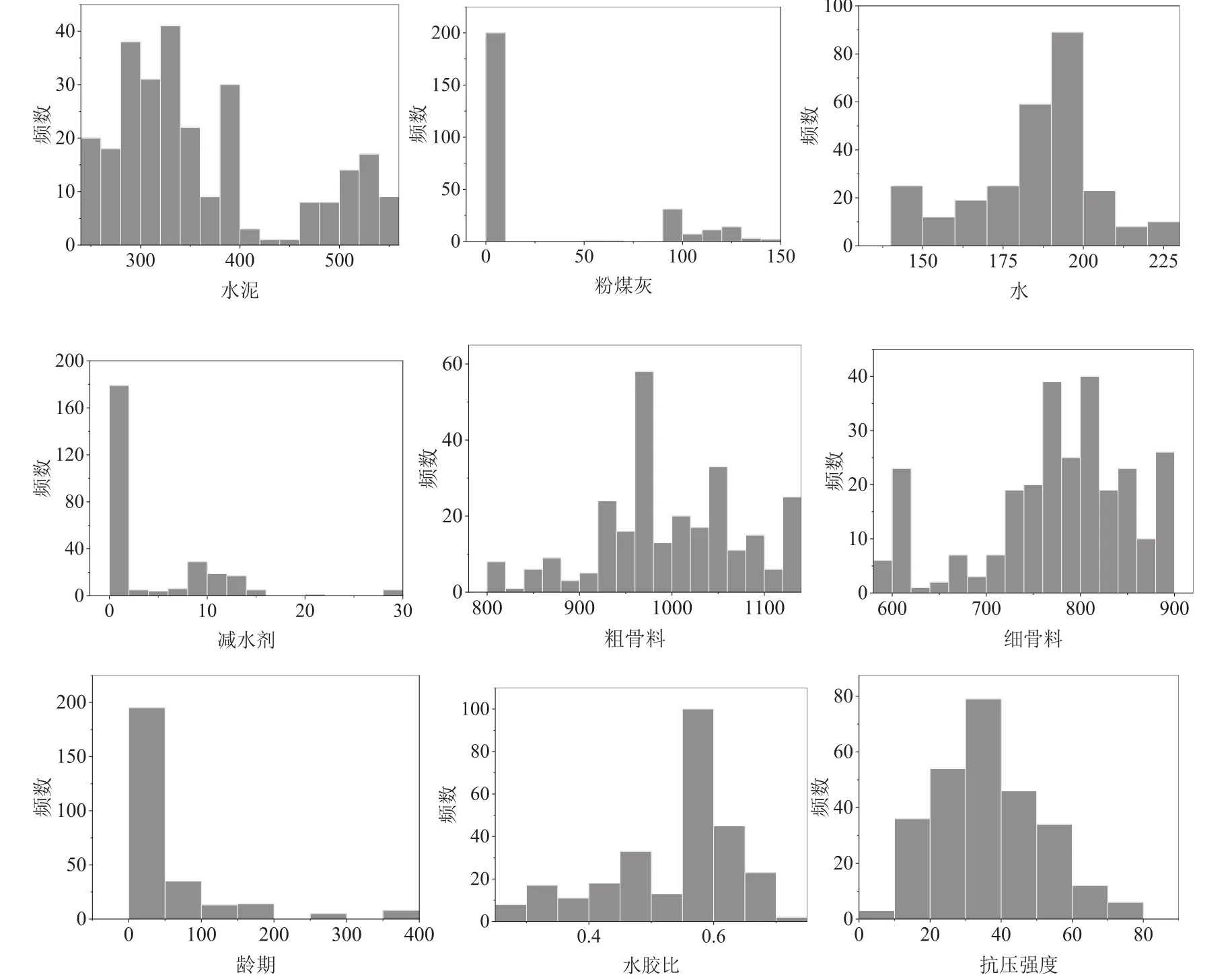
图2 输入和输出变量的分布直方图

表1 参数的统计特征

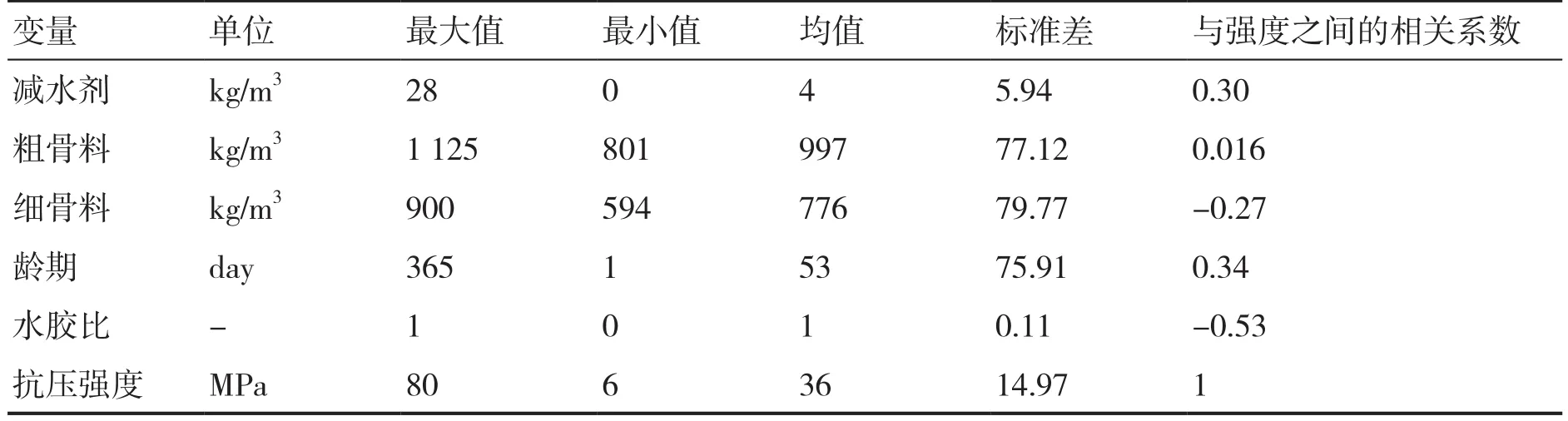
表1（续）

为了量化模型训练和预测的效果，引入相应的评价指标[12-13]。这些指标的计算公式是:

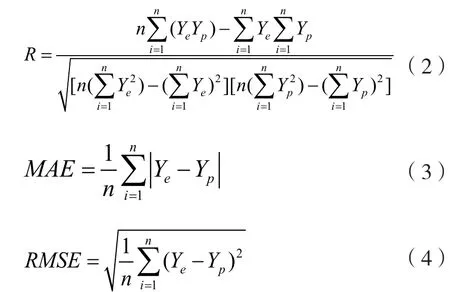
其中R可以反映预测抗压强度和实际抗压强度之间的相关性，R越接近1表示相关性越强。误差指标可以反映预测抗压强度和测量抗压强度之间的偏差和分散程度。式中Ye是抗压强度的真实结果，Yp是抗压强度的预测结果。

3 模型预测结果比较

模型的训练和测试结果如图3所示。从图3可以看出，相比于ELM和SVR，随机森林模型无论训练还是预测其结果的相关系数R是最高的，均超过了0.93。图4展示了每个样本点的实际值和预测结果之间的比值。在预测结果的基础上计算对应的误差评价指标如图5所示。对于随机森林而言，MAE 和RMSE均是三种模型中的最小值，表明误差越小，预测准确率越高。

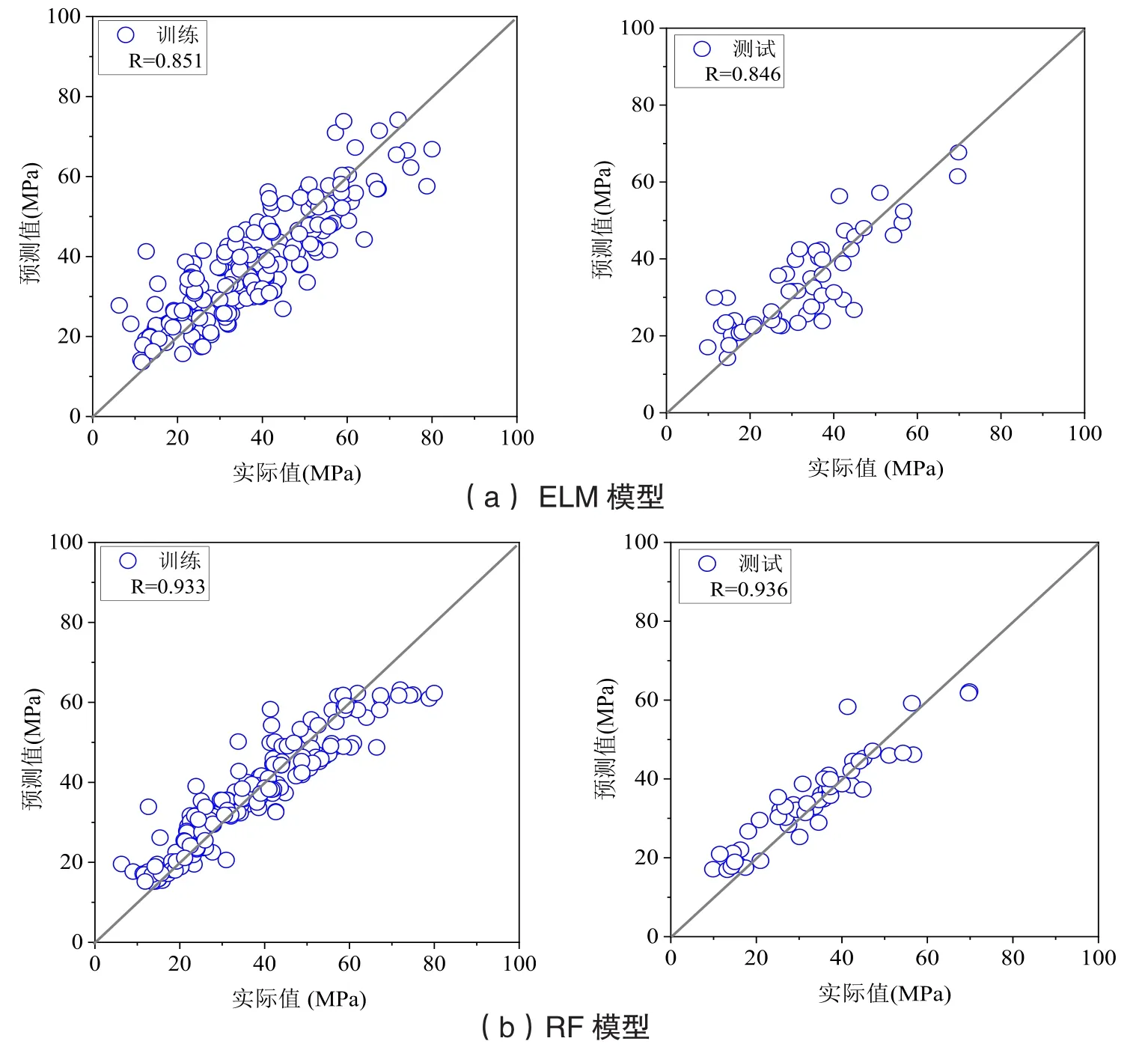
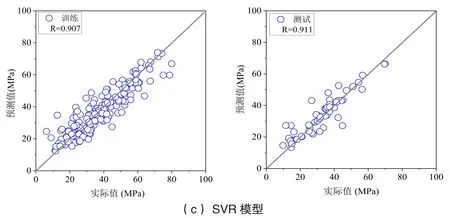
图3 三种模型预测结果与实际值之间的相关性

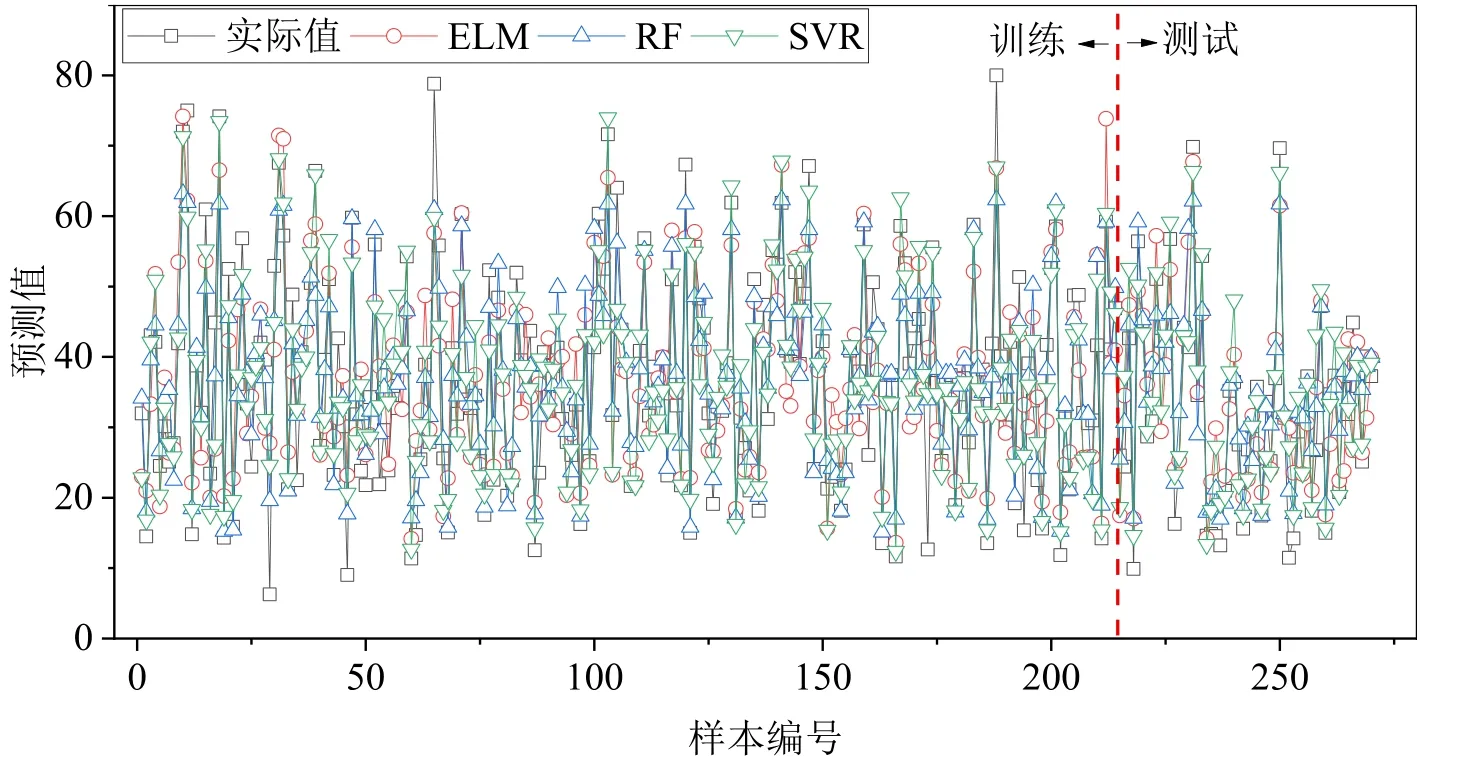
图4 模型训练和测试结果

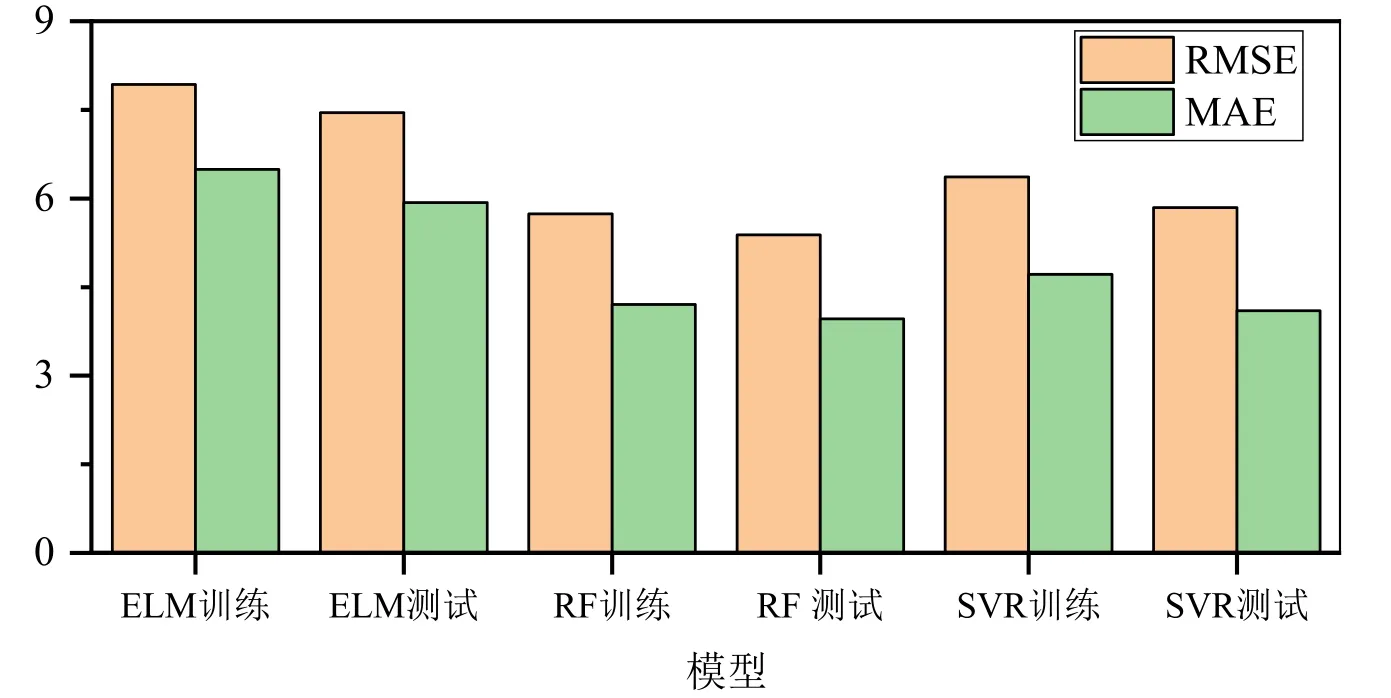
图5 三种模型的误差评价指标

4 结论

①本文所介绍的三种机器学习算法均可以有效地映射出多输入参数和输出抗压强度之间的复杂非线性关系。

②相比于极限学习机和支持向量回归模型，本文所提出的随机森林模型预测精度高，预测误差更小，建议推广至工程实践使用。

③本文所提的抗压强度预测方法可以部分替代实验室压缩试验，大大减少实验工作量，对科学研究和工程应用具有重要的参考意义。