天然气用印刷电路板换热器多孔介质模型研究

陈望男， 许子瑞， 马文贺， 林 军， 邓全文， 王雪超， 马 挺

(1.西安交通大学 热流科学与工程教育部重点实验室，西安 710049；2.克拉玛依市富城能源集团有限公司，新疆克拉玛依 834000；3.中国石油工程建设有限公司，北京 100120；4.北京师范大学 地理科学学部，北京 100875)

符号说明：

μ——动力黏度，kg/(m·s)

vp——多孔介质模型的速度，m/s

vc——实际模型的速度，m/s

qm,N——各通道的质量流量，kg/s

δp——压降的相对误差

p——压力，Pa

σ——孔隙率

si——在i方向的动量方程源项

dh——当量直径，m

ρ——流体密度，kg/m3

Hm——局部压力损失，Pa

l——流动方向的长度，m

Φ——流动不均匀度

D——黏性阻力系数

C——惯性阻力系数

Re——雷诺数

f——达西摩擦因数

n——通道数

Hf——沿程压力损失，Pa

η——局部压力损失与总损失的比值

d——换热器宽度，m

Δxi——长度，m

C1、C2——常数

为了应对气候变化，我国将“碳达峰、碳中和”纳入国家总体发展战略。作为一种低碳能源，天然气的开采、运输和利用越来越引起人们的关注。印刷电路板换热器(PCHE)因换热性能好、结构紧凑和耐高压等优点，在液化天然气领域具有很好的应用前景。然而由于印刷电路板换热器的通道数量多、结构复杂，对整个印刷电路板换热器进行建模难度很大，而且需要大量的计算资源。而多孔介质模型可以大幅简化通道内部细节，为印刷电路板换热器的整体模拟提供了可能。

多孔介质模型被广泛用于管式换热器的数值模拟中。Ma等[1]利用多孔介质模型，对比分析了4种不同结构类型管翅式换热器的流动不均匀性，通过优化导流结构，流动不均匀性降低了42%。Ma等[2]利用多孔介质模型研究了空气入口速度和温度对制冷系统管翅式换热器压降和传热效率的影响。Ding等[3]使用多孔介质模型，研究了在高超声速预冷发动机中管壳式换热器的流动不均匀性。Li等[4]对管翅式换热器进行模拟，其中翅片部分利用多孔介质模型，其他部分使用实际模型，结果表明由多孔介质模型得到的速度分布与实际模型的结果非常吻合。屈帅丞等[5]使用多孔介质模型模拟了齿形翅片管式换热器的压降，同时探究了几何参数对多孔介质模型精确度的影响。唐凌虹等[6]基于多孔介质模型探究了进风角度对椭圆管翅式换热器流动性能的影响。张友森[7]使用多孔介质模型对大型多管束降膜蒸发器进行了三维数值模拟研究。Kim等[8]将复杂的U形管式换热器分为垂直直管束、弯管束和水平直管束，每段分别用一个多孔介质域进行模拟，通过与实际CFD模型和实验对比，证明了多孔介质模型可用于此类换热器模拟中。Urquiza等[9]使用多孔介质模型得到整个印刷电路板换热器的速度场。Zhu等[10]利用多孔介质模型模拟了紧凑型换热器的压力和速度场，探讨了在整体模型尺寸一定的情况下，通道数量对多孔介质模型精度的影响。然而，国内外研究工作主要是对多孔介质模型在印刷电路板换热器的整体传热和阻力性能进行分析，对于单通道的多孔介质模型参数用于多通道印刷电路板换热器模型的准确性还缺少深入分析。

笔者针对天然气用印刷电路板换热器，利用多孔介质模型，探究单通道求解的多孔介质模型参数应用于多通道印刷电路板换热器的可行性，并分析了通道长度、换热器宽度和入口雷诺数对多孔介质模型精度和流动不均匀性的影响，旨在分析多孔介质模型用于天然气流动特性预测的可行性 。

1 数值模型及数值方法

1.1 数值模型

所研究的印刷电路板换热器以超临界甲烷为工质，选取换热器的一组通道进行二维模拟。流体从入口封头流入，再分流到芯体部分的各个通道，然后从出口封头流出。芯体部分的通道宽度为0.5 mm，通道间距为0.5 mm，通道数为n，通道长度为L，换热器宽度d=n×a，其中a=1 mm，入口、出口封头的长度分别为Lin和Lout，且Lin=Lout=d；入口、出口封头的宽度分别为din和dout，且din=dout=d/2。图1为n=8，L=200 mm时的模型。

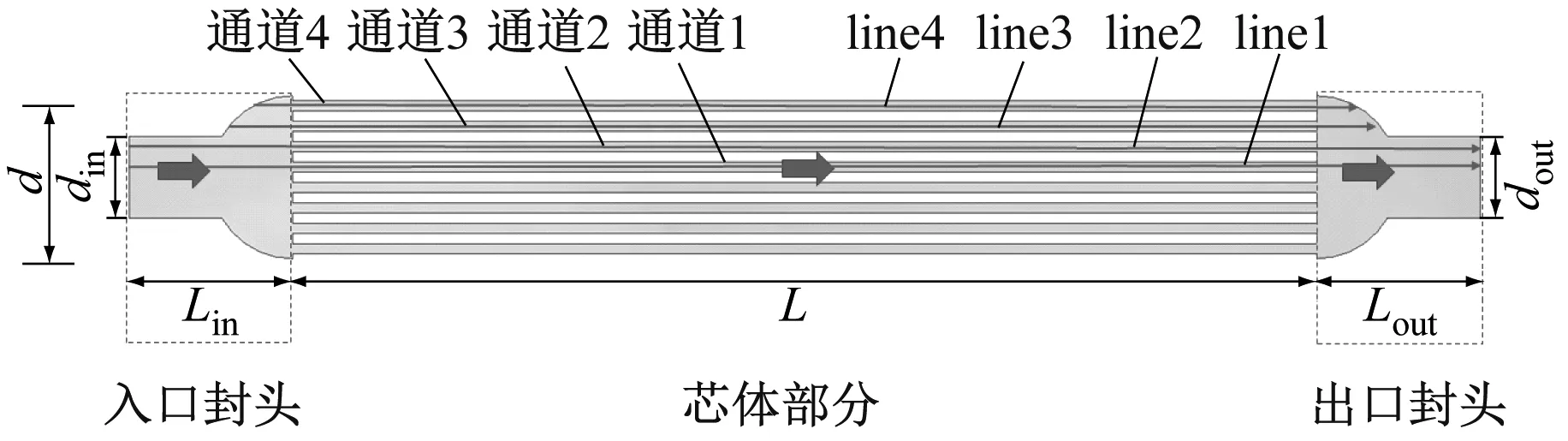
图1 实际模型(n=8)Fig.1 Actual model(n=8)

不同通道数的实际模型如图2所示。为研究换热器宽度对计算精度和流动不均匀性的影响，保持通道宽度为0.5 mm，通道间距为0.5 mm，L=200 mm不变，取n=4、8、16进行研究，即换热器宽度d=4 mm、8 mm、16 mm。

为研究通道长度对计算精度和流动不均匀性的影响，保持芯体部分通道的宽度为0.5 mm、通道间距为0.5 mm和通道数n=8不变，取L=100 mm、200 mm、300 mm、400 mm进行研究。当量直径dh=1 mm，L/dh>60[11]时，可不考虑入口效应。

图2 不同通道数的实际模型Fig.2 Actual model with different number of channels

在多孔介质模型中，所有尺寸、进出口段的结构与实际模型保持一致，芯体部分使用多孔介质域代替实际通道，以简化模型。当n=8，L=200 mm时，实际模型与多孔介质模型的对比如图3所示，其中MC8代表通道数为8的实际模型，PM8代表通道数为8的多孔介质模型，当通道数变化时采用类似的表达方式。

图3 实际模型与多孔介质模型的对比Fig.3 Comparison of actual model and porous medium model

1.2 边界条件

所采用的工质是340 K、6.5 MPa条件下的超临界甲烷，由NIST-REFPROP软件求得其密度为39.192 kg/m3，动力黏度为1.350 5×10-5kg/(m·s)。2种模型都采用速度入口边界和压力出口边界。在计算层流时，超临界甲烷的入口速度为3.45×10-2～4.13×10-2m/s，Re≤1 200；在计算湍流时，超临界甲烷的入口速度为3.45～10.34 m/s，10 000≤Re≤30 000。实际模型壁面采用无滑移壁面；多孔介质模型中进出口封头的壁面采用无滑移壁面，芯体部分采用有滑移壁面。在计算湍流时，实际模型采用SSTk-ω湍流模型,由于多孔模型中的动力源项已包含湍流,因此采用层流模型。速度和压力的耦合采用Couple算法，所有方程均采用二阶精度迎风格式，设置的收敛残差为10-6。

1.3 流动特性评价指标

为了对印刷电路板换热器流动不均匀性进行量化，引入衡量通道间流量分配不均匀程度的指标，即流动不均匀度Φ[12]：

(1)

在多孔介质模型和实际模型位于最中心位置的通道(如图3中A点、D点连线所示)中分析这2种模型的压降相对误差，计算公式如下：

(2)

(3)

多孔介质模型的进出口压力不会出现突降或突增的情况。然而在实际模型中，由于进出口处存在局部压力损失，压力会出现突降或突增的情况。局部压力损失与总损失的比值为：

(4)

1.4 多孔介质模型

多孔介质模型是一种对实际模型的简化模型。对于含有众多空隙的结构，例如土壤、过滤网和管束等，直接建立实体模型存在几何建模复杂、网格数量大且提高网格质量难度系数大、计算耗费资源大等问题[5]。因此，利用多孔介质模型代替实际模型可省去建立实体模型的过程，大大降低了几何建模的难度和网格数量。多孔介质模型在流体流动控制方程的动量方程上叠加一个动量源项[5]，即

(5)

在印刷电路板换热器实际模型中，压降Δp的计算公式如下：

(6)

(7)

(8)

根据式(5)～式(8)可以确定多孔介质模型的黏性阻力系数和惯性阻力系数：

(9)

(10)

2 模型验证及多孔介质模型系数确定

2.1 网格无关性验证

对n=8、L=400 mm的实际模型和多孔介质模型进行网格无关性验证，结果如图4所示。最终确定实际模型的网格数量为284 752，多孔介质模型的网格数量为22 152，多孔介质模型的网格数量远小于实际模型的网格数量。

(a) MC8网格无关性验证

2.2 模型有效性验证及系数确定

基于通道间距为0.5 mm、初始通道长度L0=100 mm单通道的数值模拟，可以得到f=f(Re)。f随Re的变化如图5和图6所示，层流区域数值模拟结果与解析解f=96/Re[13]非常吻合，湍流区域内数值模拟结果与实验数据[14]一致，平均相对偏差小于5%。因此，单通道的多孔介质模型是有效的。C1、C2可表示为：

(11)

(12)

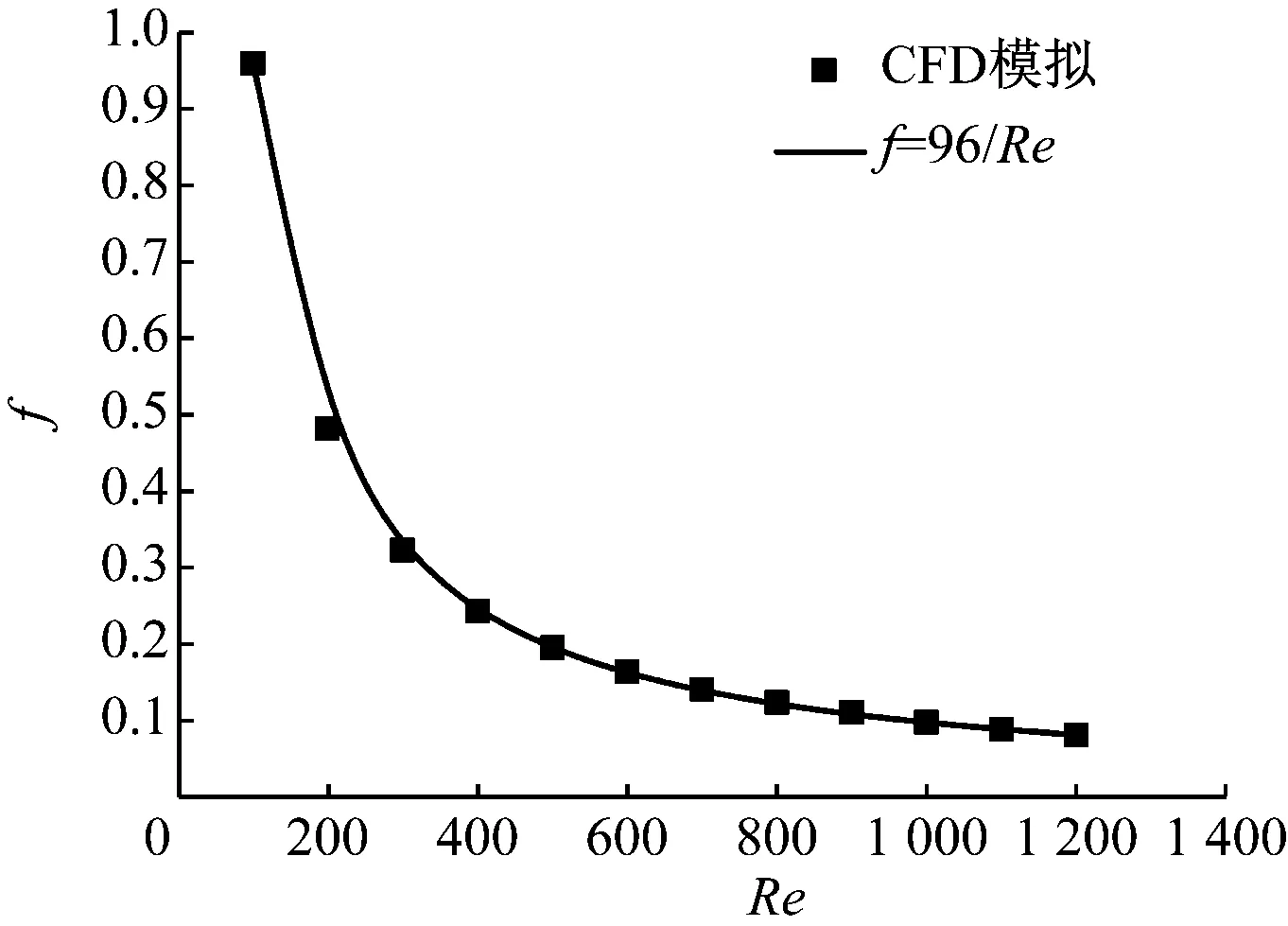
图5 f随Re的变化(层流)Fig.5 Variation of f with Re (laminar flow)

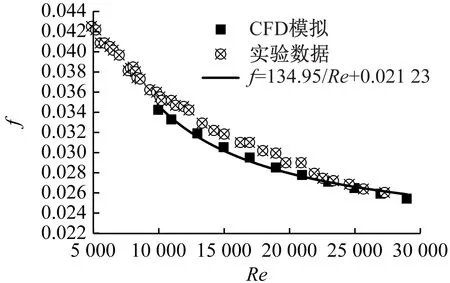
图6 f随Re的变化(湍流)Fig.6 Variation of f with Re (turbulence flow)

3 结果与分析

3.1 雷诺数对压力和流动不均匀度的影响

实际模型与多孔介质模型的压降随Re的变化如图7所示。由图7可知，2种模型的压降沿流动方向的变化趋势一致，随着Re增大，2种模型的压降相对误差δp变大。在Re≤1 200时，2种模型的δp小于5%。流动不均匀度和局部压力损失与总损失的比值随Re的变化如图8所示。由图8可知，随着Re增大，2种模型的Φ均增大。在相同的情况下，多孔介质模型的Φ大于实际模型的Φ。随着Re增大，η增大，局部压力损失的占比增大导致2种模型的Φ增大。η会影响流动不均匀性：η越小，反之Φ越小；η越大，Φ越大。

图7 2种模型压降随Re的变化Fig.7 Variation of pressure drop with Re for two models

图8 Φ和η随Re的变化Fig.8 Variation of Ф and η with Re

不同Re下的压力云图如图9所示。由图9可知，在Re=400时，多孔介质模型的入口段开始出现回流，但实际模型并未出现回流情况。回流导致多孔介质模型的最外侧通道的流量减少，造成多孔介质模型的Φ大于实际模型的Φ。由图9还可知，当n=16、L=200 mm、Re≤1 200时，多孔介质模型能很好地预测实际模型的压力场。

3.2 换热器宽度对压力和流动不均匀度的影响

不同换热器宽度下多孔介质模型和实际模型各通道的流量分布如图10所示。换热器宽度d=4 mm、8 mm、16 mm，Re=100时实际模型和多孔介质模型各通道的流量分布相同。随着Re增大，最外侧通道的流量表现出一定的差异。如图11所示，随着换热器宽度变大，2种模型的Φ减小，流动越来越均匀。当Re≤1 200时，2种模型的Φ<0.2%。

(a) Re=100

(a) d=4 mm

图11 d=16 mm时不同模型的流动不均匀度分布Fig.11 Flow nonuniformity of different models when d=16 mm

3.3 通道长度对压力和流动不均匀度的影响

在保持Re=10 000,n=8不变的情况下,分析通道长度对压力和流动不均匀度的影响。由图12可知，多孔介质模型和实际模型的压降沿流动方向的整体变化趋势相同。但是在流体从入口封头进入芯体部分的通道时，实际模型由于流通截面的突然变化，会发生局部压力损失而使压力骤降或骤增；而在多孔介质模型中，由于芯体部分用一个整体的多孔介质域代替，芯体部分的阻力损失是速度的函数，因此压力变化不会出现骤降或骤增的情况。由图12还可知，随着L的增大，2种模型的δp变小。当L=100 mm时，δp=25%；当L=400 mm时，δp=8%。

不同通道长度下多孔介质模型和实际模型各通道的流量分布如图13所示。随着L/L0增大，实际模型的各通道流量逐渐趋于一致。但是多孔介质模型中的最外侧通道的流量远偏离于其他通道，随着L增大，流量偏离情况有所改善但不明显。这就导致多孔介质模型的Φ始终大于实际模型的Φ。由图14可知，随着L增大，2种模型各通道的Φ越来越小。同时，当L从100 mm增大到400 mm时，η从24%减小到8%，而相应的实际模型的Φ从0.6%减小到0.2%。随着L增大，η减小，2种模型的流动变得均匀。

(a) L=100 mm

(a) 实际模型

4 结 论

(1) 在层流(Re≤1 200)范围内，随着Re增大，多孔介质模型和实际模型的Φ均增大。在相同的情况下，多孔介质模型的Φ大于实际模型的Φ。2种模型的δp均小于5%，多孔介质模型能很好地预测实际模型的压力场。随着换热器宽度变大，2种模型的Φ减小。2种模型的Φ<0.2%，多孔介质模型能很好地预测实际模型的流动不均匀性。

图14 不同通道长度下的流动不均匀度分布Fig.14 Flow nonuniformity under different channel lengths

(2) 在保持Re=10 000,n=8不变的情况下，随着L增大，多孔介质模型和实际模型的δp和Φ均减小。当L=400 mm时，压降相对误差小于10%。当换热器宽度和雷诺数保持不变时，增加通道长度有利于提高多孔介质模型预测实际模型的精度。