基于密度峰值聚类和径向基函数的过采样算法

陆妙芳，杨有龙

西安电子科技大学 数学与统计学院，西安 710126

在数据集中，如果存在某些类的样本数量多于其他类的样本数量的情况，就出现了不平衡。样本数量较多的那一类称为多数类，相对应的，样本数量较少的类称为少数类。这种类与类之间存在的不平衡问题称为类间不平衡问题。传统的分类器都是针对平衡数据集而设计的，在处理不平衡数据时就会出现偏向于多数类的现象，从而导致少数类样本的不正确分类，进而是分类性能的下降[1]。当训练集处于高度不平衡状态时，少数类样本甚至可能被忽略，为了达到最好的分类效果，仅仅对多数类正确分类[2]。例如，在一个包含了1 000个样本的二类数据集中，一类的样本数量为998，而另一类的样本数量只有2。传统的分类器为这样的数据集分类时，只要正确地分类多数类样本，就能达到99.8%的分类准确率，少数类样本不会被检测。如果这是一个罕见疾病的诊断，错分少数类样本意味着未能将疾病病例诊断出来，就会导致患了疾病的患者错失最佳治疗时机，甚至为此付出生命。这样的代价是人们万万不想见到的。因此，不平衡数据分类问题的研究是极为重要的。

在现实生活中，不平衡数据也是无处不在的。特别是在医疗疾病诊断[3]、信用欺诈检测[4]、网络入侵检测[5]、文本分类[6]等领域。过去的20多年中，由于不平衡数据集分类问题的难度及普遍性，研究学者们提出了许多方法来解决它。解决不平衡数据的方法主要分为三类：数据级方法、算法级方法、分类器集成方法。

数据级方法：通过数据预处理的方式，使用重采样技术来平衡数据的类分布。重采样技术包括过采样、欠采样和混合采样[7]。过采样通过增加少数类样本的数量来平衡数据集。过采样方法中较为流行的是Chawla 等人[8]提出的综合少数类过采样（SMOTE）方法，该方法通过在原少数类样本及其近邻样本中间线性插值生成新的少数类样本。但这种方法没有考虑多数类的样本分布，可能会产生噪声样本。为弥补这一不足，Bunkhumpornpat 等人[9]提出了安全水平过采样（Safe-Level-SMOTE）方法，该方法通过为少数类样本分配安全水平值来选择合适的样本以合成新少数类样本，安全水平值定义为k个近邻中其他类样本的个数，但生成的样本大多数离分类边界较远。边界过采样方法（Borderline-SMOTE）方法[10]首先识别类边界，然后对接近类边界的少数类样本过采样。但该方法只考虑了近邻的数量，而没有将所有靠近类边界的少数类样本纳入考虑范围。前面的这些方法大多是基于近邻进行过采样。Yang 等人[11]提出了一种基于马氏距离的采样方法，该方法的目标是使生成的新少数类样本与其对应的类均值有相同的马氏距离[12]。Cieslak 等人[13]提出了基于K-means 的过采样算法，该算法通过K-means 将少数类样本集划分为几个子簇，再分别对子簇过采样。Bunkhumpornpa 等人[14]提出一种基于密度的过采样算法，将少数类划分为几个任意形状的子簇，然后在随机选择的少数类样本和它对应的子簇的伪簇中心之间生成新样本。但这两种基于聚类的过采样算法容易造成重叠且无法识别边界样本。欠采样通过移除多数类样本平衡数据集。最先提出的欠采样方法为随机欠采样（RUS），该方法通过随机地移除多数类样本来平衡数据集。Anand等人[15]提出了一种基于加权的欧氏距离的欠采样算法，利用加权的距离对多数类样本进行排序，按照排列顺序移除样本。Kubat等人[16]提出一种单侧选择的欠采样算法，把Tomek links算法和CNN算法结合起来用在不平衡问题中，检测出多数类中的冗余样本和噪声样本，并将其删除。还有基于聚类的欠采样[17]，先对数据集聚类，再随机删除每个簇的多数类样本。混合采样是过采样和欠采样的结合。Song 等人[18]提出了一种基于K-means 的双边采样方法，用K-means 方法分别为多数类样本和少数类样本聚类，再为多数类子簇保留距离簇心近的样本，同时为样本量少的少数类子簇过采样。

算法级方法：修改现有算法或创建新算法，使其适用于不平衡数据集。此类方法需要研究者对待改进的学习算法有很好的了解，并能准确地知道待改进算法在学习不平衡数据时失败的原因。单类学习算法是一种算法级上解决不平衡数据分类问题的方法。此类算法专门用于处理高度不平衡数据集，它只学习少数类样本，而不对多数类样本进行学习，从而得到一个分类器。这类算法的主要目的是对高密度的目标类区域进行估计，用来描述数据。它的任务是识别目标函数，设置有效阈值是这个算法的关键。如果阈值过于紧凑，可能目标类的某些样本就会被放弃，而如果阈值过于宽松，非目标类的样本则会被误认为是目标样本。代价敏感度方法[19]的思想是不同类别的误分类惩罚是不相同的。此类方法会给少数类样本设置更高的误分类惩罚，在训练时，错分了少数类样本就会有更大的惩罚，这样最终得到的分类器对少数类的分类准确率就会提高。这种方法虽然能够有效地提高少数类的预测精度，但有一定局限性。一方面，很多情况下，只知道少数类的误分类代价比较高，但实际实践中，很难准确地估计分类成本。另一方面，虽然许多学习算法如神经网络、决策树等可以直接使用代价敏感度，但也有不能够直接利用代价敏感度的算法。在不能直接利用的情况下，只能通过调整数据集中各类别样本的比例或设置阈值的间接方式来进行代价敏感度学习。

分类器集成方法：将采样技术与Bagging或Boosting结合，对最终学习到的所有分类器投票。如SMOTEBoost[20]、RUSBoost[21]、OverBagging[22]等。该类方法已被证明能有效地解决数据集不平衡问题。例如，Easy-Ensemble 和BalanceCascade 方法，EasyEnsemble 利用随机欠采样方法将不平衡数据集均分为几个平衡的数据子集，再用集成方法处理数据集。BalancedCascade 对多数类样本进行随机欠采样以创建第一个训练子集，再利用这个子集训练获得的分类模型来预测训练子集的类标签，从训练子集中移除正确分类的多数类样本，并在其位置上添加新的多数类样本，这样，就有了一个新的训练子集。

尽管目前还没有一种方法可以很好地解决所有的不平衡数据分类问题。但采样方法在处理不平衡数据集的分类问题上已表现出很大的潜力。因为采样方法的目的是平衡数据集而不是改进分类器，可以独立于分类器而存在。平衡后的数据集可以用所有传统分类器进行分类，有广泛的适用性。

类间不平衡并不是影响分类器处理不平衡数据集时的分类性能的唯一原因。研究发现，类内不平衡、类间重叠和小间隔都可能导致分类器在处理不平衡数据集时有较差的实验效果。类内不平衡发生在少数类样本存在多个子簇并且其中一些子簇的样本数量少于其他子簇的样本数量，或者由于缺乏足够的采样而分布稀疏的情况下。类重叠发生在来自不同类的一些样本在部分或者全部特征中具有非常相似的值的情况下。小间隔发生在少数类有多个子簇，并且这些子簇至少有一个被多数类样本所包围且被包围的子簇的样本数量比其他子簇的样本数量少的情况下。

现有的算法不能同时解决这些问题，但与其他方法相比，基于聚类的采样方法在处理具有类内不平衡和类间不平衡问题的数据集时有巨大的潜力。由于欠采样可能会删除携带重要信息的多数类样本，所以本文主要关注过采样技术。目前，大多数基于聚类的过采样算法都是基于K-means 的算法。但K-means 通常只适用于超球形数据且聚类的簇数需要事先给定。而密度峰值聚类方法能解决不同形状和大小的数据集，且对密度峰值聚类算法加以改进可以使算法自动地确定簇中心。

大多数过采样算法在合成新样本时只关注少数类样本的分布，而忽略多数类样本的分布，所以容易造成重叠问题。基于径向基函数的过采样方法利用相互类分布信息来合成新样本，可以同时考虑多数类样本的分布和少数类样本的分布，避免了重叠。

针对二类数据集的类间不平衡和类内不平衡问题，以及大多数过采样算法只考虑少数类样本的分布而忽略多数样本分布的缺陷，本文提出了基于密度峰值和径向基函数的自适应过采样方法。该方法使用密度峰值聚类方法对少数类聚类，自动确定子簇个数，将少数类样本划分为几个簇，再根据子簇的局部密度给每个子簇分配权重，通过权重计算每个子簇需要生成的少数类的样本数。另一方面，该方法用径向基函数为少数类样本计算相互类势，通过相互类势的大小选定作为生成新少数类样本的原样本，最后为少数类生成新样本。

1 基于密度峰值自适应过采样

1.1 自适应的密度峰值聚类算法

密度峰值聚类（density peaks clustering，DPC）算法[23]于2014 年被提出，它是一种基于密度的聚类算法。该算法有两个简单且直观的假设：簇中心有最高的局部密度，簇中心之间有相对较大的距离。根据这两个假设，DPC 算法首先需要确定簇中心，然后依次将每个样本分配到离它最近且局部密度较高的簇中。由于DPC算法实现简单且聚类效果较好，目前已被应用到许多领域[24]。从DPC算法的两个假设出发，需要引入两个重要的量，样本点xi的局部密度ρi和局部密度比xi大的最近邻的距离δi。假设数据集为X={x1,x2,…,xn}T，其中n为数据集的样本数，对于每一样本xi，用高斯核函数计算它的局部密度ρi：

其中，dqiqj为样本xqi和样本xqj之间的距离。δqi被定义为xqi的近邻中比它局部密度高的样本与它本身的距离，具有最大局部密度的样本xq1的δq1被定义为最大δqj,j≥2值，从而保证xq1具有更大的δ值。一般来说，局部密度和距离都较高的样本最有可能是簇中心。通常以ρi为横坐标，δi为纵坐标画二维决策图，然后根据决策图将右上角的点选为簇中心，但这种方法不能自动地确定簇中心。为了使算法能够自动地确定簇中心，首先将δi和ρi归一化：

最后将i ＞icut的si对应的所有样本都确定为簇中心。确定簇中心后，就可以为其他样本点分配相对应的聚类标签。DPC 的分配策略是每个样本的聚类标签与其局部密度较高的最近邻之一相同[23]。

1.2 δ 值的改进

为了解决数据集具有不同密度和大小的问题，这里基于样本的局部比例信息引入了一种补偿策略。对于给定样本xqi，xqj为局部密度大于xqi局部密度的任意样本。为了使簇中心能够脱颖而出，将δqi定义为样本xqi和xqj的最小距离乘以它们的k个近邻的距离，具体表达式为：

1.3 自适应各子簇过采样量

现有的基于聚类的过采样方法中，过采样后所有子簇的大小都趋于一致。但这只解决了因大小不同而造成的类内不平衡问题，实际上，类内不平衡还可能是由于子簇的复杂性和密度不同而造成的。Nekooeimehr等人[26]提出了一种基于分类复杂性和交叉验证的自适应确定过采样子簇大小的方法。但该方法对分类器比较敏感，且分类复杂度会受到类间不平衡的影响，显著提高了计算复杂度。Douzas 等人[27]提出了一种过采样分布策略，在少数类稀疏区域合成更多的样本。该方法以子簇内所有少数类样本的平均距离作为密度，导致算法对异常值极其敏感。本文将使用DPC算法的局部密度为每个子簇分配过采样量。

假设少数类被分为C个子簇Cminj,j=1,2,…,C，每个子簇Cminj的密度SDminj和权重Weightminj定义如下：

其中，m是总过采样量，本文将其设置为多数类样本数与少数类样本数的差值。

1.4 基于径向过采样

使用过采样方法处理不平衡数据时，最为关键的一步是选择感兴趣的区域，即放置生成的新少数类样本的区域。过于集中的区域会导致过拟合现象，如随机过采样方法生成的新样本容易造成过拟合。若将新样本放在高密度的多数类样本区域，又会对多数类的正确分类造成影响。基于邻域的过采样方法如SMOTE算法及其衍生算法在处理具有噪声、异常值和不相交数据分布的复杂数据集时，生成的新样本容易与多数类样本重叠。此类现象产生的原因是这些方法在生成新样本时只考虑了少数类样本的分布，而忽略了多数类样本的分布。

基于势的方法则利用相互类分布信息来生成新样本，既考虑了多数类样本的分布，也考虑了少数类样本的分布。这里首先介绍势的概念。对于数据集X中的任意样本，它的势代表该点与数据集的累计接近程度。也就是说，如果一个样本xi位于数据集大部分样本的附近，它的势就会比较高。使用高斯径向基函数（RBF）为其建模，势函数定义为：

其中，Xmaj为多数类样本集，Xmin为少数类样本集。

由公式可看出，高的相互多数类类势表示多数类的类势高于少数类的类势，低的少数类相互类势表示少数类的类势高于多数类的类势。而势函数代表的是样本点与样本集的累积接近程度，当某一点对于某一类的类势较高时，可以认为该点靠近该类，即该点周围分布着大量同类样本点。因此当少数类样本点的相互类势较低时，该样本点属于少数类的可能性更高。本文在此基础上，选择相互类势小的少数类样本作为原样本合成新的少数类样本。

新少数类样本的合成过程为：以现有的少数类样本xi为原样本，从它的k个近邻少数类样本中随机选取一个样本xj，再从[0，1]区间中随机取一个数t，接着生成新少数类样本，计算公式如下：

在生成新样本后，还需计算新样本的相互类势，如果其绝对值较低，则留下该样本，否则重复生成新样本的过程。

1.5 方法步骤

基于聚类的采样方法能很好地解决二类数据集的类间不平衡和类内不平衡问题，且密度峰值聚类方法适用于各种形状、大小的数据集，本文提出了基于密度峰值和径向基函数的自适应过采样算法（adaptive oversampling based on density peaks clustering and radial basis function，ADPCRBO）。算法首先利用改进的密度峰值聚类方法自适应地为少数类样本聚类，接着利用密度峰值聚类过程中计算所得的局部密度为少数类自适应过采样量，然后利用考虑了相互类分布信息的径向基函数为少数类选择合成新样本所需的原样本，最后再以径向基函数的值的大小为依据保留合成的新样本。算法的具体步骤如算法1所示。

算法1 ADPCRBO算法

输入：训练集X，近邻数k，参数β，迭代次数iteration。

输出：新少数类样本集Xnew。

步骤1 令Xnew=∅。

步骤2 将X分为多数类Xmaj和少数类Xmin。

步骤3 使用改进的DPC 算法为Xmin聚类，得到C个子簇Cminj,j=1,2,…,C。

步骤4 用公式（10）～（12）为每个子簇Cminj计算子簇的过采样量OSminj。

步骤5 对于子簇Cminj中的任意样本xi，用公式（14）为其计算相互类势。

步骤6 用公式（15）生成一个新的少数类样本xnew，并计算其相互类势Φnew。

步骤8 重复步骤6、步骤7，直到满足迭代次数。

步骤9 将生成的少数类样本放到Xnew中。

步骤10 返回Xnew。

2 实验结果与分析

2.1 实验数据集

为了验证算法的适用性，本文实验用到了KEEL上的8个数据集。本文是针对二分类不平衡问题的研究，所有数据集都是二类的。为了说明本文算法在不同程度的不平衡数据集中都适用，本文选取的数据集的不平衡率有低于10 的，也有高于80 的。数据集的详细信息如表1所示。

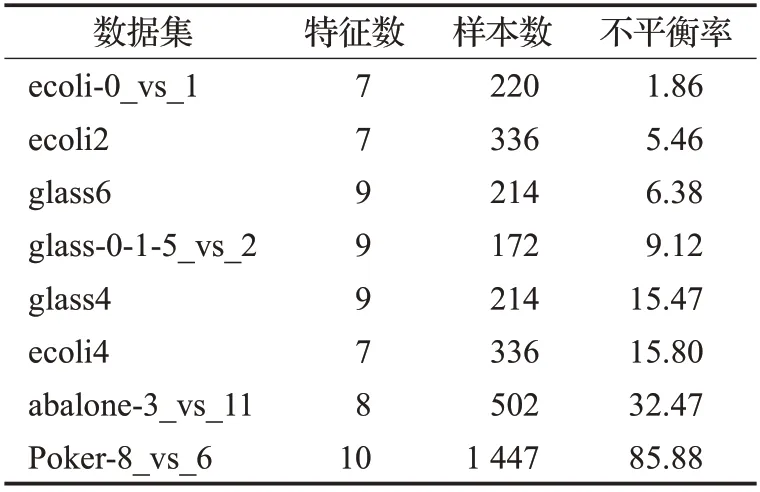
表1 实验数据集Table 1 Experimental datasets

2.2 实验设置

为了验证算法的有效性，实验中将本文算法与六个对比算法进行对比，对比算法分别为：RUS、SMOTE、Borderline-SMOTE、Safe-Level-SMOTE、K-means-SMOTE、SMOTE-RUS。其中包含了过采样方法、欠采样方法和混合采样方法，用不同方法与本文算法比较以便更好评估算法的分类性能。

因算法在每个分类器上的实验效果不一样，一种算法并不是在所有分类器上都取得好的分类效果。故本文的实验中，选用三个分类器与本文算法及对比算法结合进行实验。三个分类器分别是多层感知机（MLP）、k近邻（KNN）和决策树（Tree）。

同样的，算法用不同指标来评价分类效果获得的结果是不尽相同的。本文使用三个分类评价指标对算法进行分类性能的评估。这里，首先介绍一个常见的分类评价工具——混淆矩阵，其表示如表2所示。

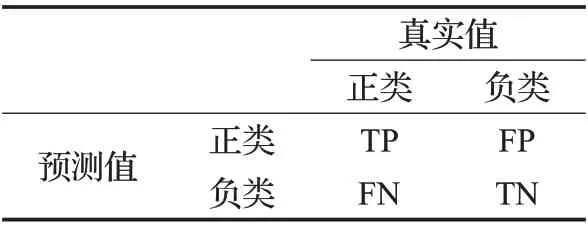
表2 混淆矩阵Table 2 Confusion matrix

一般将少数类记为正类，多数类记为负类。本文用到的评价指标基于表2而得。

（1）Recall，正类样本被正确分类的比例：

2.3 实验结果及分析

为了使实验更具有客观性，避免结果受随机的影响，本文使用交叉验证法进行实验，重复实验10次再取平均结果。

表3～表5 分别表示本文算法与对比算法结合MLP分类器、KNN 分类器和决策树在实验数据集上进行分类实验所得的AUC 指标值的对比结果，表中加粗的数字为对比发现较好的结果。

从表3可以看出，在MLP分类器上，用AUC来评价分类性能时，本文提出的方法能在所有实验数据集上取得较优AUC值。在不平衡率较高的abalone-3_vs_11数据集和poker-8_vs_6数据集上的AUC值也较高，说明即使是在高度不平衡的数据集中，本文算法也能很好地为数据集分类。从表4 可看出，在KNN 分类器上用AUC评价分类性能时，本文算法在多数数据集中都能取得较好实验结果。从表5可以发现，在Tree分类器上用AUC评价分类性能时，本文算法能在一半以上数据集上取得好的分类效果。

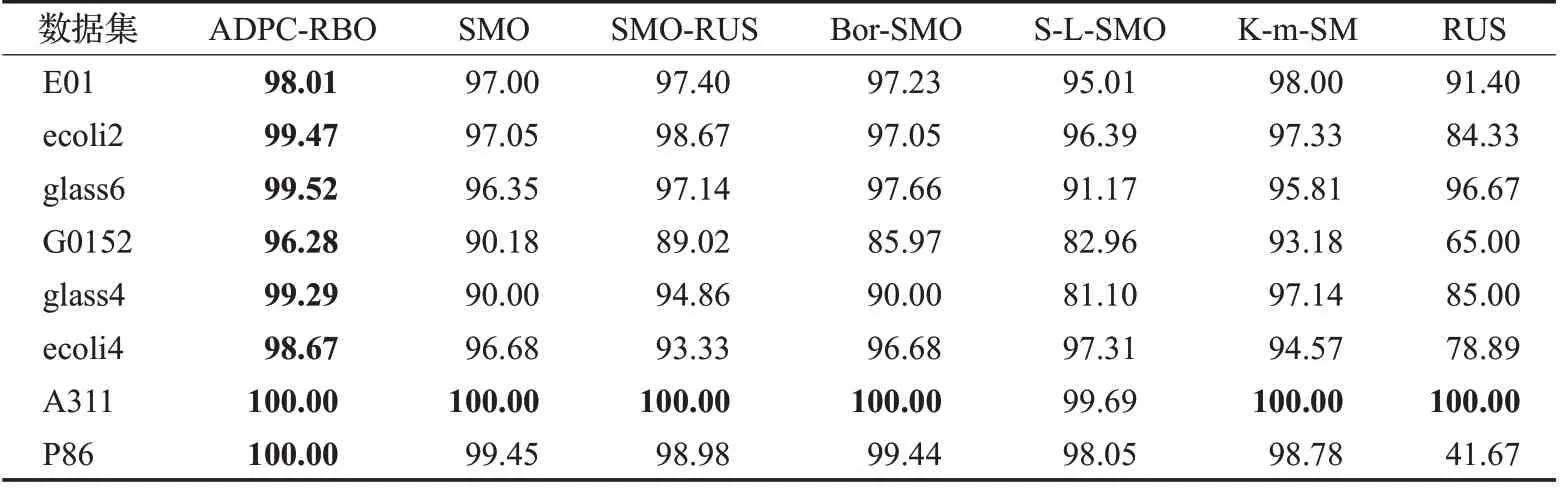
表3 各算法在MLP分类器上用AUC评价结果Table 3 AUC comparison of different menthods combined with MLP 单位：%

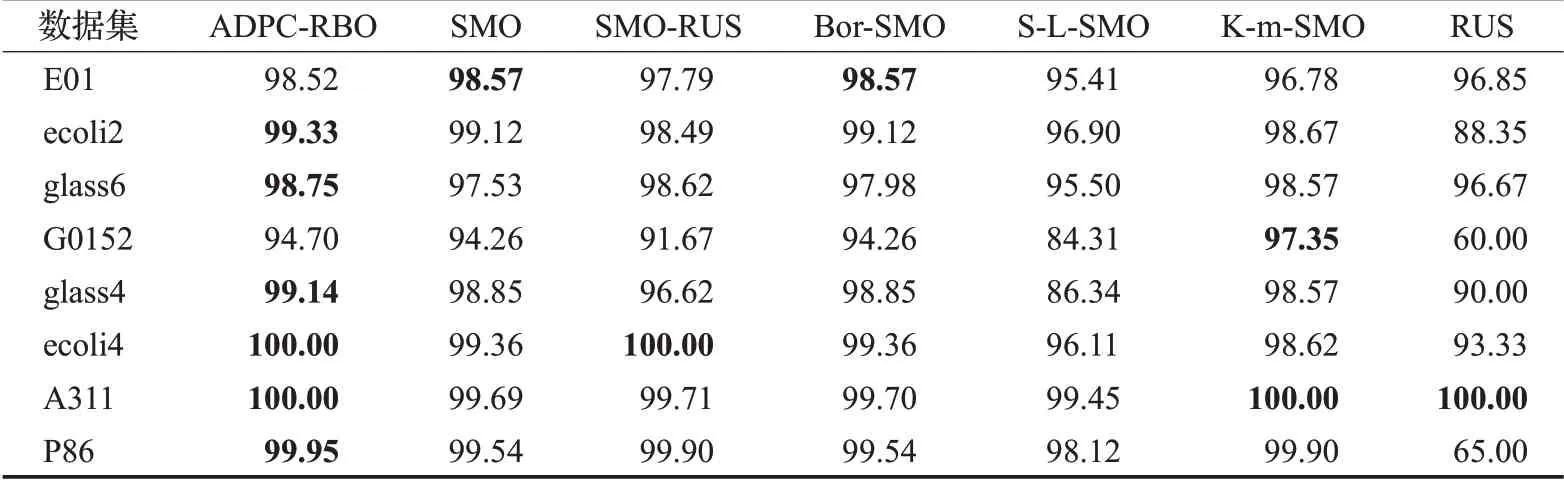
表4 各算法在KNN分类器上用AUC评价结果Table 4 AUC comparison of different menthods combined with KNN 单位：%

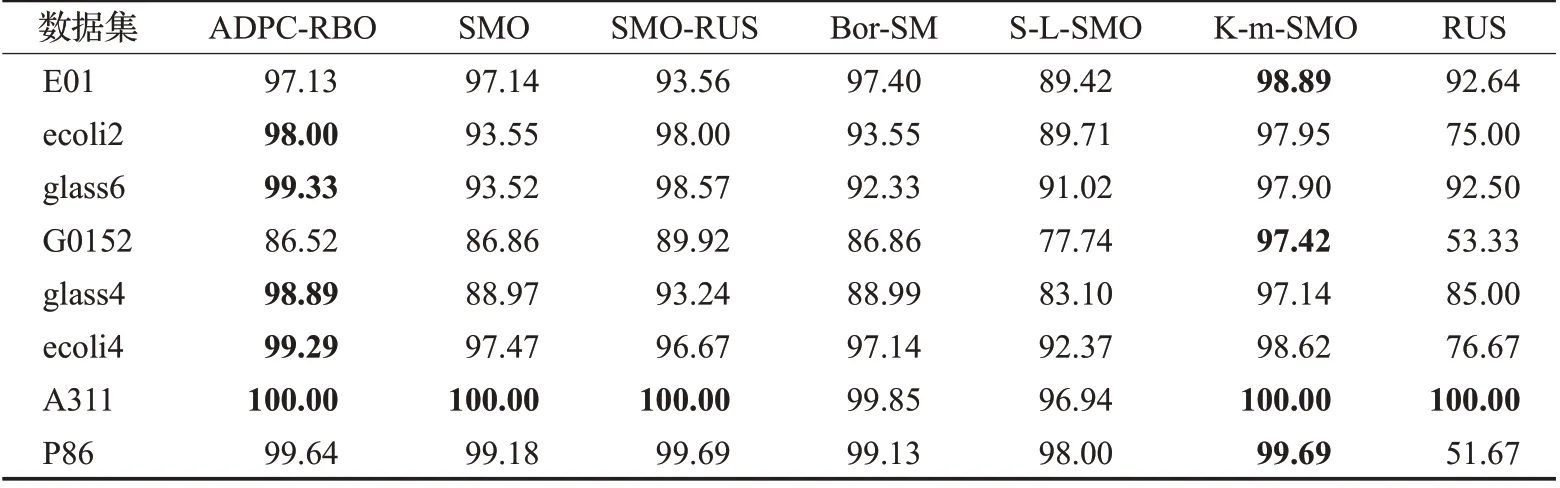
表5 各算法在决策树上用AUC评价结果Table 5 AUC comparison of different menthods combined with Tree单位：%

对比三个表格，不难发现，本文算法与MLP分类器结合进行实验的实验效果是较好的，与KNN 分类器结合进行实验的实验效果次之，与Tree分类器结合进行实验的实验效果略差。这表明，与不同分类器结合对算法的分类性能是有一定影响的。实验时，应为算法找到一个合适的分类器，以便应用到实际问题时能更好地为人们服务。

图1～图3 是本文算法及对比算法结合三个分类器在实验数据集上进行实验的指标值对比结果。在对比图中，绿色表示本文算法优于对比算法，黄色表示本文算法与对比算法有等同实验效果，红色表示本文算法比对比算法差。

从三个对比图中可看出，结合三个分类器进行实验时，本文算法的分类效果都是较优的，能在大多数数据集上取得较好的结果。具体来说，在与MLP 分类器结合进行实验时（实验结果如图1所示），本文算法能取得更好的实验结果，用三个指标评价的结果都优于其他算法的。与KNN分类器结合进行实验时（实验结果如图2所示），用三个指标来评价，本文算法都能在一半数据集上取得较优实验结果。与决策树分类器结合进行实验时（实验结果如图3所示），仅在用AUC指标评价的情况下，能优于对比算法，用其他两个指标评价时的效果较差。分析三个对比图还可看出，当用AUC 指标评价分类效果时，本文算法的分类效果均优于对比算法的。

综上所述，本文算法在与MLP、KNN、Tree 分类器结合进行实验时，都能取得较好的实验结果。用AUC指标评价分类结果能取得较高的值，表明本文算法整体分类性能较优。

3 总结

针对二类数据集的类间不平衡和类内不平衡问题，本文提出了一种基于密度峰值和径向基函数的自适应过采样方法。对于数据集具有不同密度和大小的问题，引入基于样本局部比例信息的补偿策略，使簇中心能够脱颖而出。同时将多数类样本的分布信息加入考虑范围，用径向基函数为少数类选取用于合成新样本的原样本。通过将算法在不同平衡率的数据集上与不同分类器结合进行实验，并用不同评价指标评价分类性能，验证了本文算法的有效性。本文算法只研究了二类问题，实际上，多类不平衡问题在现实生活中更普遍存在，下一步将探讨算法在多类不平衡数据集中的应用。