离群点检测的邻近性方法综述

刘财辉，刘地金

赣南师范大学 数学与计算机科学学院，江西 赣州 341000

数据的邻近性度量可以分为相似性和相异性两个方面，它们相互构成负相关关系。在数据挖掘应用中，通常用数据矩阵和相异性矩阵来表达这两种特性，以此来评估对象之间的相似程度或相异程度[1]。

在离群点检测中，邻近性包括距离和密度两种典型的近邻方式。所以，基于邻近性的离群点检测方法包括基于距离的方法和基于密度的方法。前者是利用距离计算方法来衡量数据样本的离群程度，后者则是对局部数据簇的密度情况来判断数据局部离群程度[2]。

离群点被定义为一个显著不同于其他数据分布的数据对象，通过分析离群点数据分布特征，可以从海量数据中挖掘异常信息、提取兴趣模式等。因此离群点检测（outlier detection）成为数据挖掘领域的研究热点之一[3]。离群点检测目的是通过数据挖掘方法找出不同于大规模数据中的异常点，并发现潜在的、有意义的知识。目前其广泛应用于欺诈检测[4-5]、医疗处理[6]、公共安全[7]、环境卫生[8]、图像处理[9]、异常行为模式检测[10]、轨迹异常检测[11]等领域。传统离群点的检测方法众多，一般经典的离群点检测方法通常分为基于统计学的、基于聚类的、基于分类的和基于邻近性的方法四大类[3]。

邻近性方法的核心思想是定义出数据之间的邻近性度量，并根据此度量的值判定离群点。其中比较典型的方法是基于距离的方法以及基于密度的方法，前者以距离体现邻近性，后者以密度体现邻近性[12]。

本文通过综述基于邻近性的离群点检测方法，包括基于距离的检测方法和基于密度的检测方法。目前，梅林等[12]对传统的离群点检测方法和目前主流的检测技术进行了系统化的综述，但由于介绍的面比较广，缺乏对某一小领域的精细研究。针对这个问题，文献[13]对基于聚类领域的离群点检测方法进行了综述。为了完善离群点检测方法在更加精细化邻域的研究，本文提出了基于邻近性的离群点检测方法的综述，目的是为后续科研人员从邻近性方面进行离群点检测研究做一个铺垫，让研究新人对邻近性的离群点检测方法有个快速的了解。

1 基于距离的检测方法

基于距离的方法是通过计算数据点之间的距离来检测离群值的，通常离最近的相邻点很远的数据点被认为是离群值。最常用的基于距离的离群点检测定义集中于局部邻域、k-最近邻（KNN）[14]和传统的距离阈值概念。Knorr 和Ng[15]最早对基于距离的异常值计算进行了研究。在接下来的章节中，将基于距离的方法分为以下几类——使用k近邻计算的基于距离的方法、基于求解集的方法、基于角度的方法、近邻方法、修剪方法和与在数据流中的方法以及各方法的优缺点进行总结归纳。

1.1 k 近邻法

使用k近邻方法来检测离群点与k近邻分类不同，这些方法主要用于检测全局离群点和局部离群点。首先，搜索每个记录的k近邻，然后使用这些近邻计算离群值。其关键思想是利用邻域信息来检测离群值。

1.1.1 全局离群点检测

在1998 年，Knorr 和Ng[15]提出了一种非参数方法，基于索引的算法和基于嵌套循环的算法，两种算法的计算复杂度都为O(kN2)，前者，在数据集的维数增加时具有较好的扩展性，但是时间复杂度的估算仅考虑了搜素时间。后者，它不需要构造索引结构，把数据集划分为逻辑块，通过选择每个逻辑块装入缓冲区的顺序，实现输入、输出效率的改善。这与一些统计技术[16-17]形成了对比。但这两种算法的局限性是用户缺乏关于底层分布的知识。

后来Ramaswamy 等[18]提出了一种基于网格单元的对N线性、对K指数的算法，对之前的算法[15]进行了优化。与前两种方法相比，其计算复杂度较低，适用于大规模数据集的异常值检测，但当数据集的维数增加时，它的可扩展性较差。在文献[15]的扩展版本中，使用了KD-tree、X-tree 和R-tree[19]。Ghoting 等[20]提出了一种名为RBRP（recursive binning and reprojection）的算法，提高了高维数据集的计算速度，并改进了以往方法[15，18]的缺点。使用了近似近邻，这使得计算量更少，计算速度更快，但是此方法的局限性是只适用于小数据集，对大数据集的扩展性不行。

Angiulli 等[21]的方法与传统的方法有所不同，传统的方法是开发技术来检测输入数据集中的异常值，而他们的方法可以学习模型并预测输入数据集中的异常值。他们设计了一种基于距离的算法，可以从给定的未标记数据集中检测顶级异常值，并预测一个未检测到的数据点是否为异常值。该方法的局限性是将异常值看作是二元属性，对检测出的每个异常值不能给出异常的程度。

1.1.2 局部离群点检测

2009年，研究人员将研究的方向转向了局部距离的离群值检测。Zhang等[22]提出了一种基于局部距离的离群值检测方法，称为基于局部距离的离群值因子（local distance-based outlier factor，LDOF）。与LOF[23]相比，在邻居大小范围内的性能有所提高。两两距离计算的需求为(O(k2) )，类似于COF[24]。在性能上可与k近邻离群点检测技术相媲美。但是，它对参数值不太敏感。Liu等[25]在后来的研究中，将传统的LOF扩展到不确定数据。

文献[26]给每个对象分配一个孤立程度，通过将孤立程度进行排序判定离群点。提出了一种基于近邻传播的离群点检测算法，引入放大因子。与top-nLDOF算法[22]相比，增大了算法对离群点的敏感性，以此提高算法的准确性。该方法放大离群点的离群因子，扩大与正常点的差异，很好地提高了检测的准确性与效率，但是该算法对离群点的敏感度不太理想，针对此方法的灵敏度改进将成为后续研究的有意义方向。

1.2 基于求解集（solving set）的离群点检测方法

基于求解集的方法由Angiulli 等[27]提出，主要思想是利用一个求解集来求解离群点检测问题。考虑图1所示的例子，图1（a）显示了整个数据集，那么在图1（b）中定义了一个求解集S={a,b,c}，用黑点表示。图1（c）显示了邻域关系，其中实线箭头表示数据集中对象的第一个和第二个邻域，虚线箭头表示求解集对象的第二种邻域。

为了计算离群点检测问题的求解集，相继提出了三种算法：Solving Set 算法、Robust Solving Set 算法和Minimal Robust Solving Set 算法，以适用于不同情形。这个方法的主要优点是计算时间短，因为它只计算到求解集合对象的邻域距离，而不是整个数据集。

1.3 基于角度的离群点检测ABOD方法

数据维数的增加导致了所谓的“维数灾难”，这意味着比较距离变得十分困难。文献[28]提出了一种新的方法，称为基于角度的离群点检测ABOD 方法，该方法仍然使用距离，但也考虑了所有数据对象的角度方差。该方法观察每个对象的角度方差，并计算一个名为CBOF 的离群因子，对象离聚类越远，CBOF 越小，角度方差越小（见图2）。

图2显示了ABOD方法检测异常值的过程，p为异常值，可以清楚地观察到内露层的角度比异常值的角度要宽，即γ的角度要大于α和β的角度。实验结果表明，该方法具有较高的查全率和查准率。

1.4 反向近邻方法

Radovanovic 等[29]提出了一种反向最近邻方法来解决计算高维数据集异常值检测的问题，可以有效地应用于低维度和高维环境。Huang等[30]采用自然邻域的概念来获取邻域的信息。Ha等[31]提出了一种利用迭代随机抽样确定k合适值的启发式方法。Tang 等[32]提出了一种在局部KDE中确定离群值的方法。他们研究了反向最近邻、共享最近邻和k个最近邻。基于邻域的检测方法独立于数据分布模型，易于理解和解释。然而，它们对参数设置很敏感，有时还存在性能缺陷。

文献[33]针对分布复杂且离群类型多样的数据集进行离群检测困难的问题，提出基于相对距离的反k近邻树离群检测方法RK-NMOD（reversedK-nearest neighborhood）。该方法定义了对象的相对距离，能同时有效检出全局和局部离群点。该方法结合了经典距离、对象局部密度、对象邻域关系。

1.5 其他近邻方法

Huang 等[34]提出了一种名为基于秩的检测算法（RBDA）的方法来对邻居进行排序，确保了高维数据的本质变得有意义。在文献[35]中说明，当物体从相同的机制中产生时，它们会彼此靠近或共享相似的邻居。后来，Bhattacharya 等[36]提出了一种进一步使用最近邻秩和反向最近邻秩的方法，确保能有效地测量每个候选对象的离群值。为了提高搜索效率，Wang 等[37]增加了使用最小生成树。

文献[38]提出一种基于随机距离方法的排名模型框架（RAMODO），利用很少的标记数据作为先验知识来学习，可以非常低维地表示超高维数据。这种基于随机距离的学习方法让离群值检测器获得更好的性能和速度，所需的标记数据也更少，在内存上，至少获得了两个数量级的加速，降低了空间复杂度。

文献[39]针对k近邻的标签噪声过滤对近邻参数k的选取较敏感的问题，提出了近邻感知（perception of nearest neighbors，PNN）的标签噪声过滤算法，可有效解决二分类数据集的类内标签噪声的问题。相比经典过滤算法，PNN获得更优的噪声识别效果，显著提升模型的泛化能力。PNN 对于多分类数据的噪声过滤具有一定借鉴意义。

1.6 修剪方法

Bay 等[40]提出了一种基于嵌套循环的算法，该算法使用了随机化和剪枝规则，能够在之前方法中显示二次性能的数据集上获得接近线性的时间[15]。然而，算法做了大量的假设，从而导致性能较差。针对文献[15，18-19]都无法同时满足CPU 成本和最小化I/O 成本的需求，Angiulli等[41]提出了一种名为将离群值将数据推入索引（DOLPHIN）的新算法来解决这些问题，只对数据集进行两次顺序扫描。

Ren等[42]提出了Ramaswamy等技术[18]的改进版本，这是一种基于垂直距离的离群点检测方法，该方法通过p-树两阶段（带剪枝和不带剪枝）进行离群点检测。Vu等[43]引入了MIRO（multirule outlier），MIRO采用了与文献[42]相似的技术，使用剪枝技术来加快异常值的检测过程。

1.7 在数据流中的方法

随着大数据的到来，许多传入的数据是连续流的形式。对于基于距离的方法，面临着重大的挑战，如时间概念、多维度、概念漂移和不确定性问题[44]。这类数据的挖掘高度依赖于时间间隔。两个著名的数据流窗口模型是边界和滑动窗口[45]。前一种方法，首先确定数据流中的一个时间点，然后分析最后一个时间点和当前时间点之间的时间点；后者方法，窗口由两个滑动端点标记。

Angiulli等[45]提出了一种对数据流中离群值进行一次性查询的新思路，不同于文献[46-47]提出的连续查询方法。他们提出了三种stream outlier miner（STORM）算法。第一种是精确算法（exact-storm），使用流管理器和合适的数据结构，缺点是存储所有窗口对象的开销且它不能装入内存。后两种算法侧重于检测近似结果，目标是通过只保留安全内层的受控部分来最小化内存使用。Yang等[48]提出了一些方法（Abstract-C、Abstract-M、Exact-N、Extra-N）来处理数据流上滑动窗口场景中基于邻接模式的增量检测。该方法解决了处理滑动窗口的问题，这是早期基于增量DBSCAN 算法[49]不支持的问题。它显示了更少的CPU 使用，并且它保持了窗口中对象数量的线性内存使用。

Kontaki 等[50]提出的算法解决了数据流事件检测中的一些问题[51]和数据流上滑动窗口场景中的事件检测[48]。在Angiulli等的技术[51]中，在检测离群值的过程，有两种算法使用滑动窗口与阶跃函数并行。文献[50]的主要目标是最小化存储消耗，提高算法效率，并使其更加灵活。Cao 等[52]提出一种称为ThreshLEAP 的算法。它是一种试图减轻昂贵的范围查询的技术，通过不相同的窗口中存储数据点来实现的。利用现代分布式多核集群来提高可伸缩性的异常值检测是未来研究的一个感兴趣方向。

1.8 与粗糙集结合的方法

文献[53]将传统的基于距离的离群点检测方法[15]与基于粗糙集边界的离群点检测方法[54]结合在一起，提出了一种基于边界和距离的离群点检测方法。该方法借助粗糙集在处理不确定与不完备数据方面的优势，能够从不确定与不完整的数据中高效地检测出离群点，设计了相应的离群点检测算法BDOD，该方法创新性比较高，是原有方法的有机结合和扩展。

文献[55]设计并实现了基于邻域值差异度量的离群点检测（NVDMOD）算法，该方法利用邻域粗糙集的粒化特征提出了改进的邻域值差异度量（NVDM）方法进行离群点检测。N-VDMOD 算法具有更好的适应性和有效性，为混合型属性数据集的离群点检测提供了一条更有效的新途径。

2 基于距离的方法

2.1 优点

（1）它们是直接和容易理解的，因为它们大多不依赖假设的分布来拟合数据。

（2）在可伸缩性方面，它们在多维空间中的可伸缩性更好，因为它们有一个健壮的理论基础，而且与统计方法相比，它们的计算效率更高。

2.2 缺点、挑战和差距

（1）在高维空间上，因为它们的性能由于“维数灾难”而下降。数据中的对象通常具有离散属性，这使得定义这些对象之间的距离具有挑战性。

（2）使用基于距离的方法时，在高维空间中的邻域搜索和KNN搜索等搜索技术是一项开销大的任务。在大型数据集中，可伸缩性也不具有成本效益。

（3）现有的基于距离的方法大多处理数据流都比较困难，原因是难以保持数据在局部邻域的分布，以及难以找到数据流中的KNN。专门为处理数据流而设计的方法例外。

同时，面临着一些挑战。大多数基于距离的方法的一个重要缺点是，它们不能很好地适应非常高维的数据集[56]。当数据维数增长时，这将影响距离度量的描述能力，在多元数据集中，计算数据实例之间的距离可能需要大量的计算，从而导致缺乏可伸缩性。未来面临的挑战是：如何同时解决低内存成本和计算时间的问题。为了解决二次复杂性的问题，提出了几种优化方法，如应用紧凑的数据结构[20，57]，使用剪枝和随机化[40]等。对于k-最近邻方法，数据集在确定最佳KNN 分数方面起着至关重要的作用，在需要阈值时选择合适的阈值是最复杂的任务之一。

在表1中，提出了一系列典型的基于距离的离群点检测算法。从计算复杂度（运行时间和内存消耗）、解决问题和缺点等方面对不同的技术进行了总结。基于距离的方法由于具有较强的理论基础和计算效率而被广泛采用。

表1 基于距离的算法综述Table 1 Overview of distance-based algorithms

3 基于密度的检测方法

将基于密度的方法应用于离群点检测是已知的最早的离群点检测方法之一。基于密度的离群点检测方法的核心原理是在低密度区域可以找到一个离群点，而非离群点（inliers）则假设出现在密集的邻域。在基于密度的离群点检测方法中，与基于距离的方法相比，应用了更复杂的机制来建模离群点。尽管如此，基于密度的方法的简单和有效性使它们被广泛地采用来检测离群点。

3.1 经典LOF算法

Breunig 等[59]提出了局部离群因子（local outlier factor，LOF）方法，这是最早的基于基本松散相关密度的聚类离群值检测方法之一。该技术利用了k近邻，LOF 的目的是为多维数据集中的每个数据对象分配一个离群值（见图3）。

数据对象p的局部离群因子计算为其局部密度与其k近邻的密度之比。LOF是局部的，因为它只考虑对象的受限制的邻居。以图3为例，可以看到两个簇“C1”和“C2”有不同的密度分布。使用基于距离的方法，不能将点“o2”识别为离群值。这就是LOF 通过使用局部离群值的概念而优于使用距离概念方法的地方。与其他异常值检测方法相比，LOF能够识别出更有意义的局部异常值。

3.2 LOF算法的改进方法

由于LOF 没有有效索引的缺点，Schubert 等[60]发现LOF 密度估计可以简化，他们提出了一种简化的LOF，用KNN距离代替LOF的可达距离。尽管简化了的LOF表现出了改进的性能，但其计算复杂度与LOF相似。

Tang 等[61]提出了对LOF[59]的改进和简化的LOF[60]，称之为基于连接的离群值因子（COF）。COF 使用链距离作为估计邻居的局部密度的最短路径，这种方法的缺点是对数据分布作了间接的假设，从而导致不正确的密度估计。然而，在LOF中哪个阈值可以被认为是离群值仍然是令人困惑的。Kriegel等[62]随后为一种被称为“局部离群值概率”（LoOP）的离群值检测方法制定了一种更稳健的局部密度估计，试图解决LOF输出异常值而不是异常概率的问题。使用LoOP 的概率评分的优点是，可以更好地比较不同数据集的离群值记录。

文献[63]提出了一种基于谱嵌入和局部密度的离群点检测算法。该算法采用迭代策略对不重要的特征向量进行高效筛查。该算法对参数的设置不敏感。提出了一种可广泛应用于局部非线性子空间中离群点检测的谱嵌入方法（LODES）。Momtaz等[64]在计算局部离群值时，通过为每个对象提供一个称为动态窗口离群值因子（DWOF）的分数来检测前n个离群值。该算法是Fan 等[65]基于分辨率的离群因子（ROF）算法的改进版本。ROF 克服了精度低和对数据集参数的高灵敏度等缺点。

3.3 处理多粒度问题

在LOF[59]和COF[61]中，这些方法都不能正确处理多粒度问题。Papadimitriou 等[66]提出了一种名为LOCI 的局部相关积分技术及其离群值度量多粒度偏差因子（MDEF）来处理这一缺陷。该方法能很好地处理特征空间中的局部密度变化，同时也能检测出遥远的聚类和隐蔽的离群点。虽然LOCI 表现出良好的性能，但运行时间较长。Papadimitriou 等[66]提出了LOCI 的近似版本aLOCI。对四叉树进行了约束，来提高两个邻域的计数速度。

Ren 等[67]提出了LOF[59]和LOCI[66]结合的方法，与现有的方法相比，LOF[59]和LOCI 结合对聚类中深度的数据点具有剪枝能力，因此效率更高。提出了一种称为相对密度因子（RDF）的方法，RDF 是离群值的程度度量，离群点是具有高RDF 值的点。文献[68]针对不确定数据集的离群点检测问题，提出了基于密度的不确定数据的局部离群因子ULOF（uncertain local outlier factor）算法。结合传统的LOF算法推导出ULOF算法，优化后的方法有效地提高了异常检测准确率，降低了时间复杂度，改善了不确定数据的异常检测性能。

3.4 结合k 近邻方法

Jin等[69]提出了受影响离群度（INFLO）的方法，利用对称邻域关系来挖掘离群值。在LOF中，没有给出正确计算集群边界实例的得分的方法。INFLO 解决了这一缺点。INFLO对引用集和背景集使用不同的邻域描述，使用k近邻和反向近邻计算INFLO 得分。图4 显示了一个对象p的INFLO 影响空间(kIS(p))如何包括它的KNN(p)和它的反向RKNN(p)。

INFLO 值越高，该对象属于异常值的概率越高。Cao 等[70]提出了一种新的基于密度的局部离群点检测（UDLO）概念，该概念针对具有离散实例特征的不确定性数据，建议使用一种精确的算法来计算实例的密度。然而，只应用了欧几里德距离度量。利用其他距离计算方法来优化算法可以作为未来的研究方向。

文献[71]针对INFLO 算法[69]存在需要对所有数据不加区分的计算其k近邻和反向k近邻点集的不足，提出了局部密度离群点检测算法LDBO，引入强k近邻点和弱k近邻点概念。在准确率不低于INFLO 算法的前提下，LDBO 算法的检测时间是相较LOF 和INFLO 算法中最少的。该方法的执行时间在一定范围内受μ值选取的影响较大，但总体上看算法执行时间还是优于前两种算法。

Keller 等[72]提出了一种高对比子空间方法（HiCS），改进了离群值得分密切相关的离群值的评估和排序。基于隔离机制的灵感，Bandaragoda 等[73]提出一种基于最近邻隔离的异常检测方法iNNE（nearest neighbour ensemble），另一种用于子抽样构建模型的离群点检测方法LeSiNN[74]，iNNE 和LeSiNN 都使用了一个集成来保证离群点检测器的稳定性。在具有数千维或数百万实例的数据集中，iNNE 的运行速度比之前基于最近邻的方法（如LOF）快得多，主要因为该方法具有线性时间复杂度和常数空间复杂度。该方法的优势是弥补了之前方法的三个缺陷，即无法检测局部异常、相关属性较少的异常以及异常被正常实例包围。

Campello 等[75]将关注点从局部离群值扩展到全局离群值，提出了一种称为全局-局部层次离群值得分（GLOSH）的算法。它基于一个完整的统计解释，能够同时检测全局和局部离群值类型。它对不同的任务都具有良好的扩展性，但该研究是基于特定的k近邻密度估计，存在一定的局限性。

3.5 数据流中的检测方法

Wu 等[76]提出了一种检测大数据流中离群点的算法。他们使用了一种称为RS-Forest的快速而准确的密度估计器和一种半监督类机器学习算法。Bai等[77]考虑了大数据中基于密度的离群点检测，提出了分布式LOF计算（DLC）方法，并行检测离群点。然而，尽管性能有所提高，但与Lozano等[78]的PLOFA算法相比，它的可伸缩性仍然不佳。文献[79]将局部离群点检测的静态数据扩展到流形数据的离群点检测，提出了基于局部相关维度的流形离群点检测算法LCDO（local-correlationdimension-based outlier detection），实验观察发现在1维和2维的流形上做了论证，为之后处理流形数据的离群点检测问题提供了良好的理论基础。

Na 等[80]对现有LOF 的数据流算法存在的两个限制：需要大量内存和不能检测到长序列的离群点。提出了一种新的数据流离群点检测算法DILOF。DILOF 在准确性和执行时间方面显著优于现有的算法。Qin等[81]提出了局部离群值语义的概念，通过利用内核密度估计（aKDE）来有效地从流数据中检测局部离群值。KELOS 是基于抽象核心中心的aKDE 策略，aKDE 可以准确而有效地估计每个点上的数据密度。aKDE和内部剪枝策略共同消除了流局部离群点检测的性能瓶颈。

文献[82]针对现有数据流离群点检测算法在面对海量高维数据流时普遍存在运算时间过长的问题，提出一种引入局部向量点积密度的高维数据流离群点快速检测算法。以保存少量中间结果的方式只对窗口内受影响的数据点进行增量计算。该算法可以在保证检测准确性的情况下有效提高数据流的离群点检测效率，并且可扩展至并行环境进行并行加速。

3.6 基于相对密度的方法

Vázquez 等[83]提出了一种新的基于数据低密度模型的异常点检测算法，称为稀疏数据观察者（SDO）。SDO 降低了大多数懒惰学习者OD 算法的二次复杂度。Ning等[84]提出了一种基于相对密度的OD方法，该方法使用一种新技术来测量物体的邻域密度。Su等[85]提出了一种高效的基于密度的方案，该方案基于局部OD法，用于处理分散的数据，称为E2DLOS。将局部离群因子重新命名为局部偏离系数（LDC）。该方法在LDC和RCMLQ的基础上，在检测精度和时间效率上对现有的局部离群点检测方法进行了改进。

文献[86]将依据正常点与离群点相对密度的差异性计算每个对象的离群值，将离群值高的对象判定为离群点的方法引入并提出了一种生成对抗网络（generative adversarial network，GAN）与变分自编码器（variational auto-encoder，VAE）结合的GAN-VAE 算法。模型的判别器能学习正常点与离群点的分类边界，生成更多潜在离群点。该算法在准确率和F1值上均有较大提高。

3.7 高维数据的检测方法

文献[87]提出了基于邻域密度的高维异构数据局部离群点挖掘算法，首先对高维数据进行区域分割，然后采取核密度来描述局部密度，计算出数据邻域密度，从而判断异构数据中的离群点。该方法几乎不受数据量和数据维数改变的影响，其挖掘时间和覆盖率指标也较优。文献[88]针对离群点检测算法LOF 在高维离散分布数据集中检测精度较低及参数敏感性较高的问题，提出了基于邻域系统密度差异度量的离群点检测NSD（neighborhood system density difference）算法。NSD算法简单易用，在检测偏离程度较大的目标对象时会大幅降低计算开销。

文献[89]在LOF的基础上结合粗糙集理论，引入属性权值概念，提出了一种基于粗约简和网格的离群点检测算法RRGOD（outliers detecting based on rough reduction and grid）。通过淘汰属性权值低于重要度阈值的属性来降低维度，从而减少了后续的计算量。文献[90]提出一种基于局部线性嵌入的离群点检测方法（OLLE），是针对高维数据的降维方法。算法使数据集的下近似中的点保持局部线性结构，保证在降维的过程中使离群点远离正常点。该方法的优势是将数据集从高维空间降至低维空间的过程能很好地保持数据的局部几何结构，且在检测离群点时，一定范围内对k不敏感。

在表2中对经典算法进行了整理，展示了在上述一些关键算法的进展。

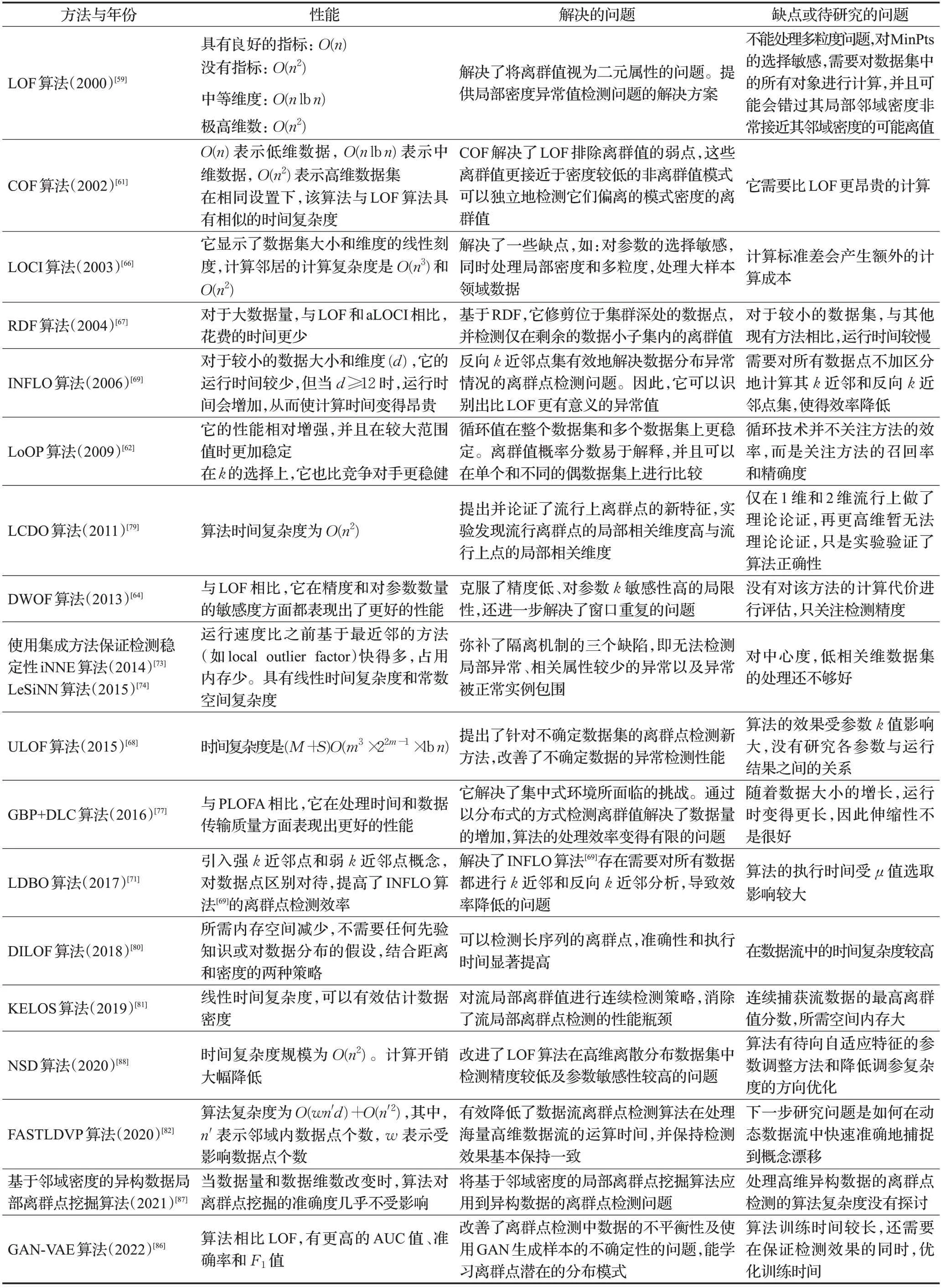
表2 基于密度的算法综述Table 2 Overview of density-based algorithms

4 基于密度的方法

4.1 优点

（1）在基于密度的方法中，使用的密度估计是非参数的，它们不依赖于假设的分布来拟合数据。

（2）一些基于密度的技术[59，62，66，69]已经成为许多后续算法的基本算法。它们的衍生算法通常优于它们的竞争对手，如一些基于统计和基于距离的方法[91-93]。这些方法中的离群值通常是通过对象的邻域密度[59]来分析的[66]，其在识别其他大多数基于离群值检测的方法所遗漏的关键离群值方面更有优势。它们只需要最小的先验知识，如概率分布和只需要一个参数调整。它们还以高效计算局部离群值的能力而闻名。

4.2 缺点、挑战和差距

（1）虽然一些基于密度的方法显示出了更好的性能，但与统计方法相比，它们更加复杂，计算成本更高[94]。它们对参数设置很敏感，比如确定邻居的大小。它们需要谨慎地考虑几个因素，这导致了昂贵的计算。对于不同密度的区域，它使性能变得更复杂并导致性能低下。

（2）由于其固有的复杂性和缺乏对离群值度量的更新，如INFLO 和MDEF 算法，不能灵活地处理数据流。当离群值之间的关系非常密切时，这对于高维数据也是一个挑战。

（3）由于大多数基于密度的方法依赖于最近邻计算，这使得k的选择对于这些算法的评估非常重要。

（4）基于密度的方法虽然检测的精准度比较高，但其复杂程度也更高，所以接下来将该方法的复杂性降低和在高维大数据集中，能有效降低计算复杂度，将是研究的重点和挑战。

5 结语

基于邻近性的离群点检测方法思想基本上贯穿于整个离群点检测过程中，依靠邻近性的思维能挖掘发现很多相似与相异的关系。本文将邻近性划分为基于距离和基于密度的两个分支，主要从邻近性角度对现有的离群点检测技术进行了归纳和分析。在离群点检测邻域，大量的方法针对不同的问题被提出，无论是基于统计的，基于聚类的，还是基于邻近性的方法，在面对现在大规模高维度数据集，检测都还存在一定局限性，随着大数据、云计算和分布式的发展，相信这些检测方法还能有更大突破。基于邻近性的离群点检测算法，最大的优点就是直观，易于理解，缺点是考虑的邻近性中的数据都要进行考虑。算法的计算复杂度如何降低、如何有效地处理高维大数据集等方向将成为以后研究的重点和热点。