几何直观视域下的试题研究
——以2021年全国新高考Ⅰ卷导数压轴题的探究为例
陈 亮 (江苏省华罗庚中学 213200)
直观想象是发现和提出问题、分析和解决问题的重要手段,是探索和形成论证思路、进行数学推理、构建抽象结构的思维基础.几何直观能力是数学能力的重要组成部分,是数学思维能力在解决数学问题中的主要体现.借助几何直观,能够使复杂的数学问题得以简化,有助于人们探索新思路、新方法,能够帮助人们从本质上理解和认识数学.本文以2021年全国新高考Ⅰ卷导数压轴题的探究为例,谈谈几何直观在代数推理和解决数学问题中的作用以及教学中的启示.
1 试题再现
(2021年新高考Ⅰ卷22题)已知函数f(x)=x(1-lnx).
(1)讨论函数f(x)的单调性;(解题过程略)

2 解题分析

2.1 基于对称的函数构造
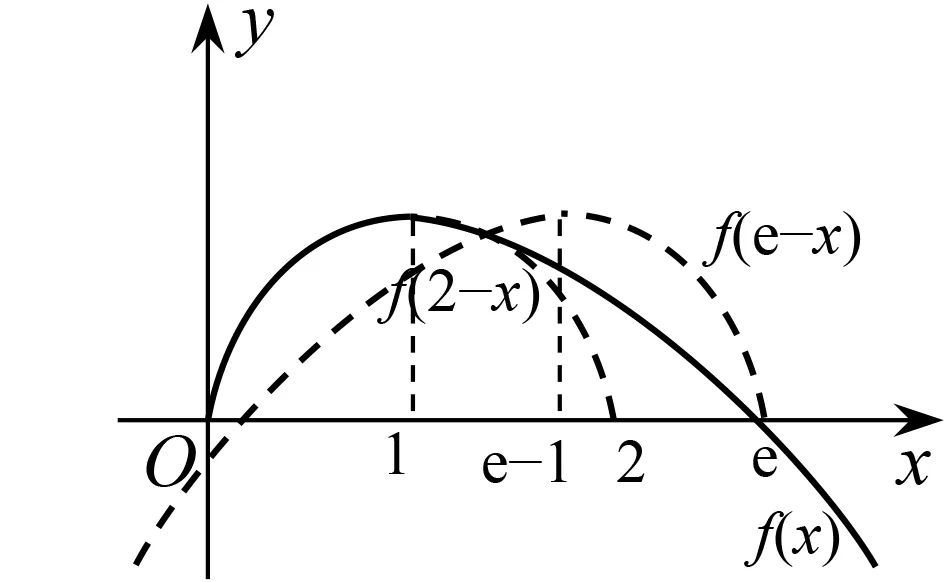
由视角①容易想到消元,然而问题的难点是:如何打通f(x1)=f(x2)与2 图1 实际上,函数f(2-x)与f(x),f(e-x)与f(x)均相互对称.如 图1,作出函数f(2-x),f(e-x)的图象可以发现,f(2-x) 函数构造的思路简洁、自然,是导数综合问题的基本思想,体现高考对基本知识、方法的考查.核心素养下的教学观并非空中楼阁,“四基”“四能”是核心素养的根基.不等式放缩的本质是以多项式函数(尤其是一次、二次函数)代替超越函数,借助多项式函数与超越函数局部具有相同性态的特点,化“超越”为“平凡”,是高等数学中的基本思想,体现了高考的选拔功能. 进一步从几何直观的角度分析x1+x2 图2 本题设计的另一个巧妙之处是直线y=e-x恰好是函数f(x)在x=e处的切线,由f(x)为上凸函数可以直观判断f(x) 本题的背景是函数极值点偏移,随着直线y=k从上往下(k值从1到0减少),x1越来越小,x2越来越大,由函数f(x)极值点“左偏”,使得x1的减少量比x2的增加量小,所以x1+x2越来越大.当k=1时,视x1,x2为两个等根,可得x1+x2=2.当k=0时,根据函数f(x)在x=0处的极限值可以补定义f(0)=0,这样就有x1+x2=e,x1+x2的取值范围是(2,e),上确界本质是由函数的极限决定的.我们可以得到以下更为一般的结论: 结论1 已知函数f(x)=x(a-lnx),x1,x2满足x1≠x2且f(x1)=f(x2),则2ea-1 学生形成和使用几何直观时有水平和层次的差异,最初是建立和形成敏捷、准确的几何直觉,感觉与图形相随;之后是实施和进行深入灵活的几何探索,视觉与思维共行;最终使几何直观成为分析、解决问题的有效工具,抽象与形象互辅[1].几何直观能力的形成不是一朝一夕的,需要教师在教学设计中逐步渗透,要将几何直观融入课程设计中. 数学新知的获取、问题的解决过程可以概括为:大胆猜测,小心论证.借助几何直观进行思考,已经成为一种重要的研究策略,在科学发现过程中起着不可替代的作用[2].教学中要引导学生善于对问题进行几何表征,从几何关系出发,借助几何直觉大胆地猜想,比如“认为直线y=e-x可能是切线”“随着直线y=k从上往下,x1+x2越来越大”,这些都是从几何直观出发的大胆猜测.借助几何模型与几何关系进行几何推理,以几何结论为目标进行代数推理,比如当我们从图形关系得到了f(x1)>x1和f(x) 几何活动经验是数学基本活动经验之一,是数学教学的目标之一,拥有丰富的几何活动经验的人,他的几何直观能力可能达到更高的水平.比如将“躺”在x轴上的线段站起来就是几何活动经验,这在利用三角函数线作三角函数图象的活动中有过;从“x1+x2>2”的构造对称函数到“x1+x2 在多数情况下,数学的结果是“看”出来的,而不是“证”出来的,所谓的“看”是一种直觉判断,这种直觉判断是建立在长期的数学活动经验之上的.几何直观能力的形成需要几何活动经验的积累,需要在教学中有目的地设计教学情境、问题链、学生活动等,帮助学生概括、提炼进而形成几何活动经验,并引导学生学会利用经验指导自己解决问题、学习数学. 康德说:“缺乏概念的直观是空虚的,缺乏直观的概念是盲目的.”数学抽象概念发展的“直观—形式—直观”模式,是一般科学概念发展的“具体—抽象—具体”模式的特殊表现形式[3],几何直观与代数推理深刻反映了数学活动的基本矛盾,代数推理通过形式化而实现精确性,又因为形式化而减弱客观性,几何直观具有原始的创造性,但又需要代数推理保证它的严谨性.代数推理具有高度抽象性,有必要再以相对直观的形式对其进行重构和深化,从而达到思维直观化的理想目标和可应用性要求,使得数学达到直观与形式的统一,以使数学更完美[3].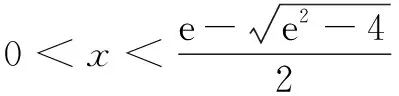

2.2 基于不等式放缩

2.3 基于几何直观的思路探求

3 溯源引流,挖掘本质

4 研题反思
4.1 几何直观是问题发现的有利工具
4.2 几何直观能力的提升需要几何活动经验的积累
4.3 几何直观与逻辑推理共同推动对数学本质的理解

