新版教材体系下独立事件的再认识
吴明德 (江苏省泰兴市第一高级中学 225400)
新版苏教版高中数学教材先讲独立事件后讲条件概率,改变了旧教材中演绎推理给出定义的方式,在逻辑上是不顺的;改用举例归纳的方法给出独立事件的定义,学生不易理解和掌握,在教学上是有挑战的.这些改变,需要我们认真应对.
1 多举实例增加感性认识
苏教版新教材必修2中通过具体事例这样给出随机事件A与B相互独立的定义:对于两个随机事件A与B,如果P(AB)=P(A)P(B),那么称事件A,B为相互独立事件.人教版由积事件的概率给出定义,侧重于事件的相互独立性是特殊的事件关系,抽象程度高;苏教版则降低抽象度,增加了一种直观判断方法,即分别计算事件A发生、不发生时事件B的概率,若相等就独立,若不相等就不独立.
需要指出的是,既然事件的独立性是概率下的等式判断,因而这种独立性更准确的名称应该是“概率独立性”,不能把事件间没有影响或事件的结果没有影响等同于概率没有影响.凭生活经验,学生可以判断一些简单事件的独立性,在直观理解无法判断事件的独立性时,定义中的概率等式就需担当大任了,相对于定义的等式判断,直觉判断的有效性显然是很弱的,有时甚至是错误的.
总体来说,将独立事件提到条件概率之前讲授,由于缺少表象的支撑,直观感知少,学生的可接受程度相对较低.我们专门做过调查,在2 512名四星级高中高一学生中,表示自己完全认可独立性定义、感觉自己深刻理解概念的人不足50%,在2 371名普通高中高一学生中这一比例更低,只有29%.相较而言,定义的必要性好理解一些,而定义的充分性则不太容易接受.
反思教学过程,我们不能因循守旧,只抱怨教材的改变,更不应期望等学习了条件概率后串联起新旧知识,化解学生的困惑.正确的做法是要重视相互独立事件的概念教学,适当增加实例情境让学生加深感受,突出独立事件的概率等式,加深概念的理解.
2 对“事件的独立性具有相互性”的解读
首先,由独立性的定义,显然可得到A与B独立,即为B与A独立.下面,我们从条件概率的角度再次对事件独立的相互性进行解读.设A与B是两个随机事件,直觉上事件A的发生对事件B发生的概率没有影响,叫做概率意义下事件B对事件A独立.设P(A)>0,若P(B|A)≠P(B),则事件A的发生对事件B发生的概率是有影响的,即B对A不独立.只有P(B|A)=P(B)时,B对A才独立.
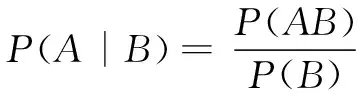
显然,P(A)=0或P(B)=0时上述推导过程不成立,为不失一般性,承认A对B独立⟺B对A独立是有难度的,但此时事件A与B满足P(AB)=P(A)P(B)却是显而易见的,这也正好说明新教材直接用积事件的概率来定义独立性的优势.
3 透过条件概率看独立事件
乘法公式P(AB)=P(A)P(B|A)普遍有,而独立事件却难得有.在学习了条件概率后,可以对独立事件的定义给出自然、合理的解释,同时也提供了让学生自主探究的素材,教学时应加以重视.
在P(A)>0的条件下,不难得到:P(AB)=P(A)P(B)⟺P(B|A)=P(B).



简证如下:

P(AB)=P(A)P(B).


4 灵活判断事件的独立性
下面对2021年高考卷中的一道概率小题略作剖析.
例(2021全国新高考I卷第8题)有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回的随机取两次,每次取1个球.甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则( ).
A.甲与丙相互独立 B.甲与丁相互独立
C.乙与丙相互独立 D.丙与丁相互独立



