基于改进粒子群的三维动画中群体路径规划
刘书艳,丁玉斌,朱云飞
(1.聊城大学东昌学院 影视传媒系,山东 聊城 252000;2.华中师范大学 物理科学与技术学院,湖北 武汉 430079; 3.清华大学出版社 第三事业部,北京 100084)
在自然界中,很多种动物总是以群体的形式生存,比如蜂群、鸟群、蚁群等等。群体中的每个动物都是个体,但个体组成了整体,它们通过简单的群体决策就可以产生强大的力量对抗外来威胁。
在计算机中模拟动物的群体行为称为群体动画,需要使得每个个体都具有相同的行为模式和目标[1-4]。群体动画在游戏、影视动画、军事等等方面已经得到了广泛的应用,它给人们带来了震撼的感观体验。但是,当群体动画中个体越多时,传统动画师消耗的时间精力就越大,这是因为个体行为无自主性,局限性较大,灵活性很差。因此,群体中的个体行为具有一定规律还要有随机性,设计群体动画中的路径规划方法是多年以来的研究热点[5],国内外研究学者也不断地完善三维动画中群体路径规划方法。
Bashath等[6]提出一种具有快速模拟退火的混合粒子群优化方法,该算法旨在解决基于两种策略的高维优化问题,即利用粒子群优化定义全局搜索区域和利用快速模拟退火细化访问搜索区域。何庆等[7]对该方案进行了改进,结合了遗传算法,使得模拟退火算法更具有自适应性。Xiao等[8]提出针蜂群算法全局探索和局部开发能力难以协调、易陷入局部最优的问题,提出了一种基于粒子群优化的蜂群算法,在收敛速度、精度和鲁棒性上都有很大的提高。Qi等[9]针对移动机器人路径规划在真实环境下优化精度低和早熟收敛的问题,提出了一种权重改进自适应人工鱼群算法。Xu等[10]通过对多灾情下恐慌情绪的产生和传染进行建模,提出了一种新的人群模拟方法。Zhang等[11]提出了一种基于分层深度强化学习的数据驱动人群疏散框架,在宏观控制层提出了一种数据驱动和深度强化学习相结合的路径规划方法,不仅可以模拟真实人群的运动行为,提高仿真逼真度,而且可以灵活地适应简单场景的动态变化,增强泛化能力。张超等[12]提出了一种基于萤火虫算法的群体动画行为控制方案,解决了制作动画中的自碰撞穿插问题。刘俊君等[13]提出了一种基于马尔可夫决策过程的群体动画模拟路径规划方法,该方法修改了不同群体行为,提高了制作群体动画的效率。朱兰[14]提出了一种基于布谷鸟算法(Cuckoo search algorithm,CSA)的群体动画行为方法,提高了行为控制的智能化。
粒子群(Particle swarm optimization,PSO)算法是模拟鸟群觅食行为的技术,其具有较高的优越性,如易实现、收敛速度快、精度高等。因此,本文提出将PSO进行改进并用于对三维群体动画角色的路径规划,生成个体的运动路径实现逼真的动画辅助设计。在Maya软件中对所提算法的路径数据进行了碰撞和群聚测试,并验证了是否具有有效性。
1 问题表述及研究思路
当前,群体动画中的群体行为的特点包括:
(1)简单性。整体中的每个个体智能化相对较简单;
(2)鲁棒性。整体的群体行为基本不会被个体行为的变化而受到影响;
(3)自组织性。在群体中,个体的运动看似随机,但是从整体而言,是一致的;
(4)独立性。群体中的每个个体都是相互独立的,且行为轨迹也是不一样的。
尽管多年三维动画中群体的路径规划方法一直在完善,但仍然有些不足之处,例如:
(1)群体动画制作过程效率较低下。传统动画制作中需要对群体中每个个体都规划路线,而且,这些路线中个体之间不能相互碰撞。传统的动画制作方法工作量较大。
(2)路径规划过程缺少交互。动画师虽然考虑个体的路径以实现避免碰撞,但对与虚拟环境交互和群体与群体之间交互的考虑较为欠缺,导致缺失了群体运动的逼真性。
(3)计算资源设备要求较高。三维群体动画制作过程中,需要较高配置的计算机处理器和显卡,才能做出更精准更细腻更逼真的动画效果,但也需要较高的成本[15,16]。
若要解决这些问题,需要进一步研究一些群体智能算法。相比其他方法,群体智能算法主要起源于模拟自然界中的动物演化、竞争行为。在解决各项进程安排和行为路线计划问题上有着较强的优势。粒子群作为研究热点的群体智能算法之一,具有较强的局部与全局搜索能力和收敛速度。因此,本文提出将PSO进行改进并用于对三维群体动画角色的路径规划,生成个体的运动路径实现逼真的动画。
2 基于改进粒子群的三维动画中群体路径规划
2.1 研究目标以及关键问题
由于群体行为的这种特殊性,要求个体的行为轨迹具有随机性,又必须整体具有一致性,最终生成的群体动画效果自然逼真。因此,研究三维动画中群体路径规划需要充分考虑以下因素:
(1)群体中的个体都有属于各自的运动区域,可以避免碰撞等现象。
(2)群体具有统一性,即整个群体的每个个体朝同方向或同目标进行运动。
(3)群体可以划分多个小群体,小群体可以根据条件自组织成新的大群体。
(4)加强逼真性。个体的运动轨迹既有独立性还要保证整体的统一性,符合群体运动的规律。
(5)提高群体协调性。加强群体的智能性,提高群体运动速度。
2.2 粒子群优化算法
假设搜索空间为N,粒子的总和为n,PSO的描述如式(1)和式(2)
vid(t+1)=vid(t)+c1×rand()×[Pbd(t)-xid(t)]+
c2×rand()×[Pgd(t)-xid(t)]
(1)
xid(t+1)=xid(t)+vid(t+1)
(2)
式中:1≤i≤n,1≤d≤N。vi(t)和xi(t)分别表示第i个粒子在第t次迭代时的速度和位置;d表示粒子i的维度;Pbd和Pgd分别表示第i个粒子的最佳位置和种群的最佳位置;c1和c2为正加速度常数;rand()表示0到1之间的一个随机数。
PSO的具体流程描述如下。

算法1PSO算法

Inputs:种群大小S;粒子i;时间t;惯性权重w;正加速度常数c1和c2;[0,1]之间的随机数rand1和rand2;
Outputs:种群最佳解Gbest;粒子最佳解Pbest;
过程:
1:创建一个大小为S的D维种群,并初始化其对应的速度向量;
2:fort=1 to 最大迭代次数 do
fori=1 toSdo
ford=1 toDdo
根据式(1)更新速度;
根据式(2)更新位置;
end
计算最新适应度函数值,更新Gbest和Pbest;
end
如果Gbest满足问题需求,则终止算法;

2.3 基于改进粒子群的三维动画中群体路径规划
尽管PSO表现较多的优势,但该算法易陷入局部最优,导致搜索精度低。为了解决这个问题,本文将具有强大全局搜索能力的引力搜索算法(Gravity search algorithm,GSA)和PSO相结合,避免PSO算法陷入局部最优解,提高粒子的全局搜索能力。改进后的算法如式(3)定义
(3)

为了使算法拥有更好的寻优能力,使用式(4)更新自适应权重
(4)
式中:fitcurrent表示当前适应度函数值,fitbest和fitworst分别表示粒子的最佳和最差适应度值。
在算法中引入一种鸟类群聚的自然行为,实现算法多样性的增强,使这算法能够探索更全面的搜索空间,避免次优解保留在搜索空间中。在每次迭代之后代理的新位置根据以式(5)更新
(5)
然而,由于后期迭代,搜索多样性可能会消失,算法极有可能陷入局部最优解中。因此,在每次迭代后严格观察Gbest的值,以确定它是否发生了改变。如果的Gbest适应性在几个连续的迭代中保持不变,则意味着粒子已处在次优位置。因此,开始了一个本地化运动过程以避免停滞,称其为对粒子调整的整体响应。
为了探索更广泛的位置,使用式(6)更新每个粒子的位置
(6)
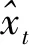

算法2基于改进粒子群的三维动画中群体路径规划算法

Outputs:粒子的最小适应度值Gbest;最佳解决方案Pbest;
过程:
步骤1所有节点(代理)在开始时随机初始化;

步骤3保持数据Xi中邻居n的索引;
步骤4通过式(6)计算每个粒子的新位置;
步骤5适应度函数作为目标函数来评估每个数据的适应度;
步骤6使用适应度函数计算节点(代理)的质量:
i∈[1,N];
步骤7计算每个粒子的引力和加速度;
步骤8更新粒子的位置和速度;
步骤9若停滞发生在最小化上,则执行步骤1;
步骤10发生个体之间的碰撞then执行步骤8;
输出目标函数值最小的最佳粒子;

3 实验结果与分析
3.1 实验配置参数
为了验证本文所提算法的有效性,对其进行仿真实验。实验仿真软件为Maya和Matlab R2018a,硬件为CPU i7、16 G内存,Window 10操作系统。实验参数设置:粒子数量N=50,最高迭代次数Tmax=1 000,重力常数G=1,加速度常数c1=c2=1.5,种群数均为50。
3.2 碰撞检测及方法
为了防止个体间发生碰撞,采用基于包围盒的随机碰撞检测算法。
粒子的包围球表示包围该粒子的最小外接球,如图1所示。

图1 包围球
粒子的包围球表示为式(7)
R={(x,y,z)|(x-x0)2+(y-y0)2+(z-z0)2 (7) 式中:(x0,y0,z0)表示球心,其通过计算粒子上坐标均值得到,r为半径。 两个粒子的碰撞检测可由包围球相交判断,判断由式(8)计算 (8) 式中:(x1,y1,z1)和(x2,y2,z2)表示两个包围球的球心,r1和r2表示两个包围球的半径。若半径和大于等于球心距,则说明两个包围球发生碰撞。 碰撞避免采用等待法和转向法。等待法是指等待个体先行通过,可用于侧面碰撞和追尾碰撞。转向法是指发生正面碰撞、追尾和侧面碰撞时,个体可转向其他无碰撞方向运动。 利用5个经典测试函数对提出改进粒子群的最优解性能进行了测试,并与典型PSO、GSA和CSA进行比较。每个函数运行次数20次。5个经典测试函数的定义如下,对比结果如表1所示 (9) (10) (11) (12) (13) 表1 测试函数对比结果 从表1可以看出,在平均优化精度方面,本文所提算法在4个测试函数中实现平均优化精度最佳,而PSO算法仅在函数f3中表现稍好,GSA算法仅在函数f2的优化中表现较好,且与本文所提算法的优化表现差距很小。对于最小优化精度而言,本文所提算法在5个基准函数中实现最小优化精度最佳。因此,本文所提优化算法在处理多维函数优化问题时能够表现出较好的搜索精度。 同时,采用f1测试函数对上述几种算法的执行效率进行了对比分析。f1测试函数50次运行后的迭代曲线分别如图2所示。 图2 函数f1的迭代曲线 如图2所示,相比典型的PSO、GSA和CSA,本文所提算法获得最优解的所需时间最小,也就是说收敛速度最快。这是因为所提算法将GSA方法和PSO相结合,从而在保证全局寻优能力的条件下加强了搜索速度。 使用 Matlab编程软件对本文所提出的基于改进粒子群的三维动画中群体路径规划算法进行实现,并将得到的路径数据导入到三维软件中进行群体动画模拟。群体碰撞避免控制过程如图3所示,群体聚集行为控制过程如图4所示,群体聚动画截图如图5所示。可以得出,本文所提出的算法具有可行性。 图3 群体碰撞避免截图过程 图4 群体聚集行为控制过程 图5 群体聚集动画截图 本文提出了一种基于改进粒子群的三维动画中群体路径规划方案。首先针对群体行为特征采用引力搜索算法对粒子群算法进行改进,以便解决粒子群算法易陷入局部最优而导致的搜索精度较低的问题,然后引入碰撞检测和碰撞避免方法,最后将算法得到的路径数据导入三维软件中进行了碰撞和群聚测试,并验证了算法具有可行性。在实验部分的标准函数测试结果中,可以看出本文所提算法具有一定的先进性,动画实例测试则证明了算法的可行性。未来,会在动画实例中增加感知模型,为每个个体都增加情感状况,这可以提高群体路径规划产生的行为逼真性。因此,后续将针对该方面进行进一步研究。3.3 标准函数测试
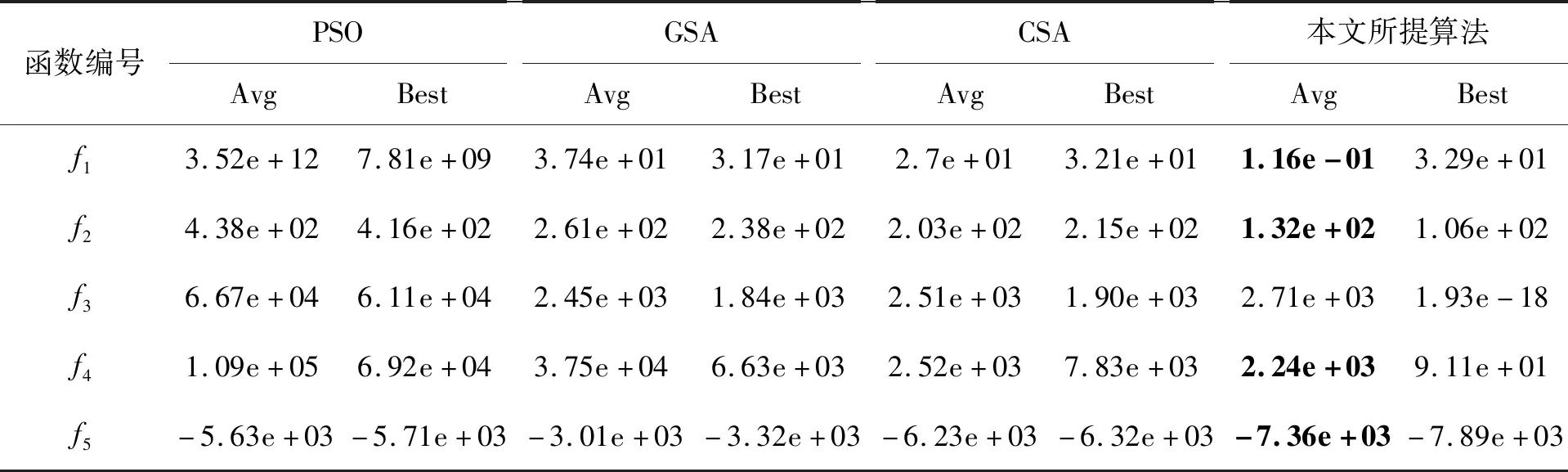

3.4 动画实例测试



4 结论

