基于格子Boltzmann方法的曲面接触热阻模拟

缪红林，张 良

（浙江大学 热工与动力系统研究所，浙江 杭州 310027）

0 引 言

接触热阻作为制约传热过程的关键热阻之一，在航天[1]、微电子[2-3]、超导[4]、能源[5]等领域的热设计和热管理中具有重要影响。 准确预测和分析导热材料间的接触热阻形成机理和规律，并实现对接触热阻特征的主动控制，对于传热器件散热结构的优化设计，提升传热性能和能效水平具有重要的意义。

现有研究表明，材料的性质，接触面的形貌特征，间隙介质、接触面载荷及环境等是影响接触热阻的主要因素[6]。 目前大量有关接触热阻的理论研究[7-8]和实验研究[9-12]工作得以开展，其中，实验研究主要围绕具体材料在不同温度、压力条件下的接触热阻特征进行测量。 实验测量法大致可以分为适用于测量较厚材料的稳态测量法[9]和适合测量薄膜材料的瞬态测量法[10]。 如冯飙等[11-12]提出的改进版稳态测量法，可用于测量亚毫米厚度材料间的接触热阻，并将测量误差控制在5%以内。

相较于实验研究，部分研究者致力于采用数值方法对不同因素的影响规律进行更为系统和深入的分析，以期望实现接触热阻的准确预测：Xiang等[13]采用非平衡的分子动力学方法模拟接触热阻，Gou 等[14]将材料真实物理形貌导入ANSYS 软件，使用有限元方法求解接触热阻。 其中，在数值模拟方法中，由于介观尺度的格子Boltzmann 方法在处理具有复杂边界的传热模型上具有一定的优势[15]，因此采用该方法对接触截面上的具有复杂形貌特征的接触热阻的计算更为有效。 在基于格子Boltzmann 方法的研究中，根据模型中热阻值是否已知，可以将之分为两类。 一种是在已知接触热阻值的情况下，在模型的接触面处添加接触热阻影响的部分反弹法[16-17]和粒子图像法[18]，这两种方法都可以在传热模型中便捷地添加接触热阻的影响。 另一种则是考虑到接触面形貌，形变模型和传热模型的建模方法：崔腾飞等[19]使用多尺度方法研究高斯表面间的接触热阻，在接触面加密网格并使用格子Boltzmann方法求解传热问题，非接触面则使用有限差分法加速计算；方文振等[20]提出的多重网格模拟方法，在接触面加密网格捕捉平直面上的分形形貌，研究平直面间接触热阻的变化规律。 与此同时，当前有关接触热阻的研究主要针对的是常见的平面上的接触热阻，而对于曲面间的接触热阻的研究鲜有报道，而曲面热阻在以内嵌管式换热器[21]为代表的传热元件中普遍存在。 准确预测固体曲面间的接触热阻，理清曲面热阻与平面热阻的共性规律与差异，对于相关传热元件的传热过程理解与优化具有重要的科学和工程意义。

因此，本文建立基于格子Boltzmann 方法的单松弛数值模型对固-固曲面间的接触热阻特征进行数值计算，并研究了温度、压力、材料和表面粗糙度四种因素对曲面接触热阻特征的影响。

1 数值模型

1.1 物理模型

本文采用格子Boltzmann 方法对两个紧密接触的等壁厚圆环在恒温边界下（Tin，Tout）的传热过程模拟计算来研究固—固曲面间的接触热阻特性。 其中，外圆半径rout为2000 μm，内圆半径rin为1500 μm，两个圆环不相互接触壁面设为绝对光滑。 该问题的计算域可以简化为如图1 所示的四分之一紧密接触的扇形，扇形内外壁面为恒温，两端为绝热。

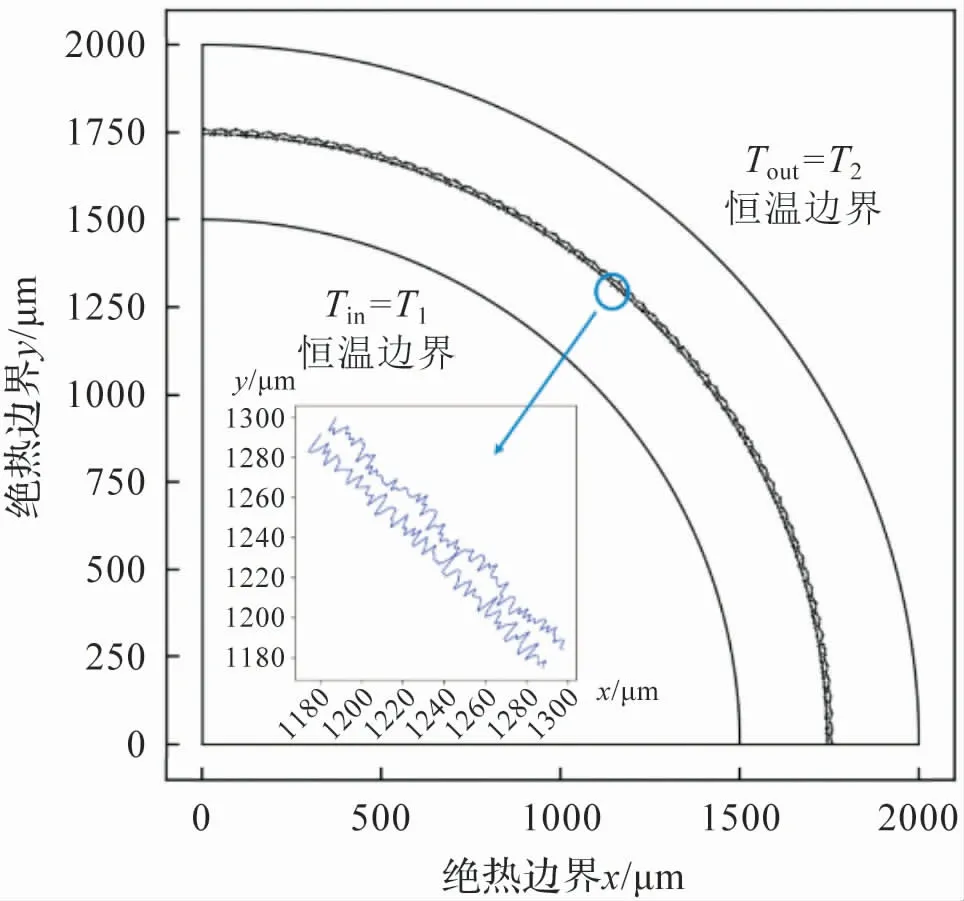
图1 接触热阻模型示意图

两个圆环相接触的圆弧表面形貌特征采用基于分形理论的W-M函数[22]进行描述，使用曲面上均匀递增的弧长作为W-M函数的参数：

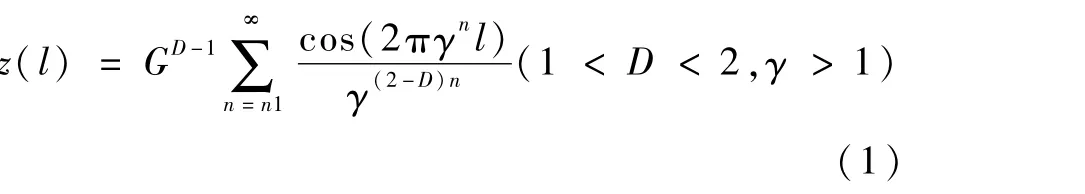
式中：z为分形形貌在曲面法线方向偏离曲面的高度；l为曲面均匀递增的弧长；G为影响特征曲面高度的分形特征尺度系数；D为影响表面复杂度的分形维数；γ为常数（对于正态分布的随机轮廓，一般取γ=1.5）；n 为自然序列。本文中选取D=1.4，G=1.0 ×10-9，n =20 ～40 生成表面形貌[23]。

接触面的粗糙度使用算术平均高度Ra表征：

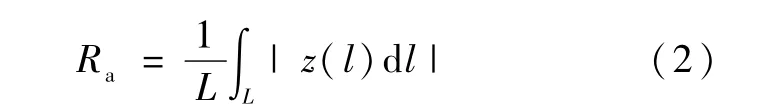
式中：L 为积分总弧长；l为积分微元；z为表面高度。

为了进一步考虑接触面上的形变特征，在接触点的形变模型上，使用CMYTCR接触模型[24]进行描述。 该模型假设接触形变是纯塑性形变，接触点的受力平衡方程为：

式中：Ar为实际接触面积；Aa为名义接触总面积；Hc为材料的微观硬度。 在模型中由于实际接触面积占总面积之比很少，因此不考虑塑性形变部分的体积变化。 故压力的计算方法：

1.2 格子Boltzmann 方法求解

根据上述物理模型及边界条件特征，其接触热阻Rtcr的表达式为：

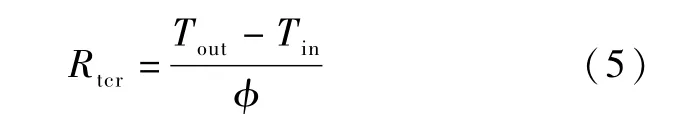
式中：ϕ为曲面上的热通量（采用二维模管，热通量单位为W/m）。 为了求得热通量，需要建立格子Boltzmann 方法对如下二维热扩散方程进行求解：

式中：T为温度；t为时间；λ为材料的导热系数；ρCp为体积比热。

本文采用单松弛的格子Boltzmann 方法求解温度扩散问题的演化方程[25]如下：

如图2 所示，速度离散使用D2Q5[26]的离散方法。 离散后的速度矢量c为：

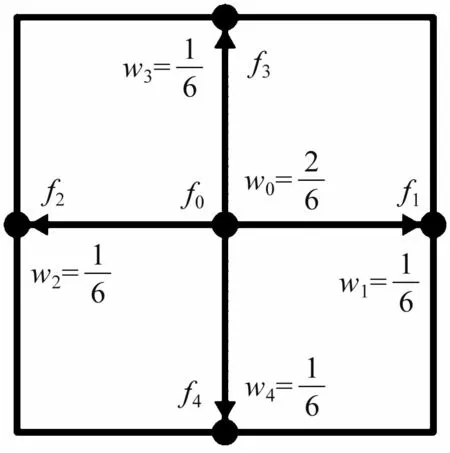
图2 D2Q5 模型

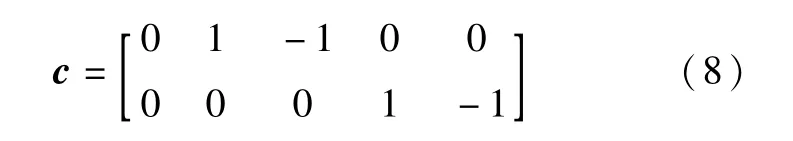
式中：q1与q2为沿分布函数迁移方向的已知热流密度，γ和β 分别为两已知热流密度与法向热流密度之间的夹角。

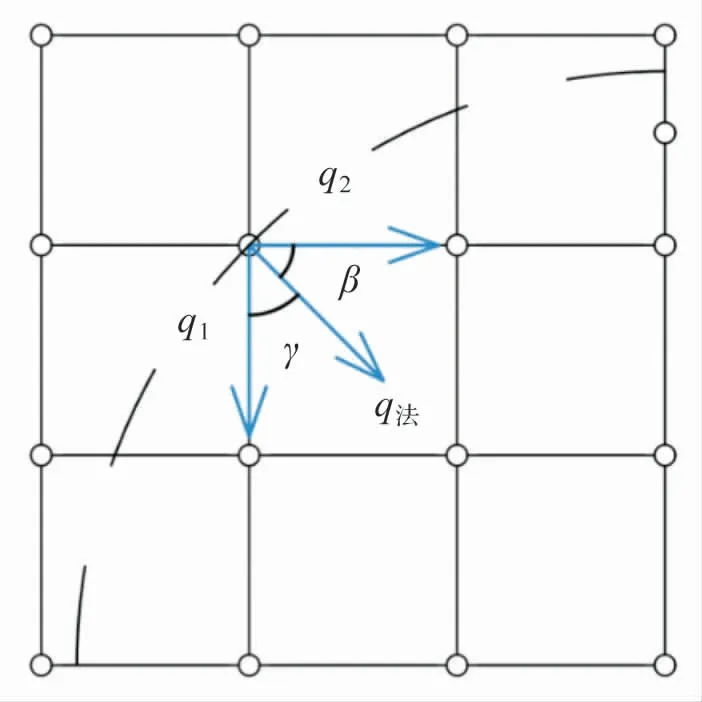
图3 热流密度示意图

在接触面间的传热过程中，以分形曲线为边界，将空间中的点划分为固体材料的点与间隙介质的点，热流需要经过固体材料，流经间隙介质到另一边的固体材料。 为保证温度与热流密度在耦合界面连续，需假设间隙介质与固体材料的体积比热相等[27]，即：

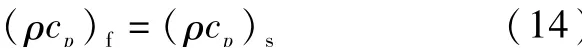
其中，（ρCp）f为间隙介质的体积比热，（ρCp）s为固体材料的体积比热。 上述假设，并不影响最终稳态的温度场。

1.3 曲面边界的处理

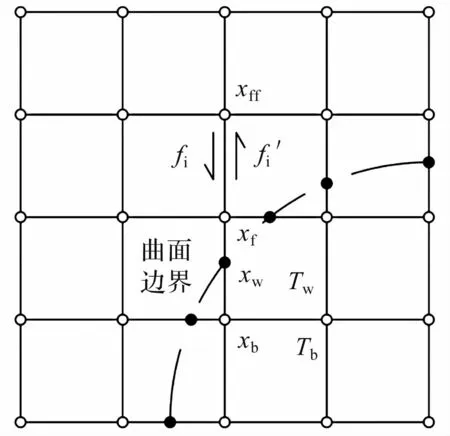
图4 曲边边界示意图

2 模型验证

为了验证本文建立的格子Boltzmann 模型计算曲面上接触热阻的可靠性，本文通过对图1 中的表面粗糙度进行理想光滑处理后进行模拟计算。 其中接触间隙取20 μm，外壁面与内壁面温度分别取303 K和293 K。 材料和间隙介质的导热系数分别取210 W/（m·K）和10 W/（m·K）。其中，热阻理论解可由以下公式直接求得：

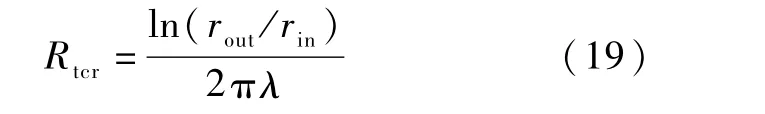
不同网格分辨率的计算结果与理论解之间的误差如表1 所示。 而且，随着网格分辨率提高，网格对计算结果的准确性影响递减。 表明本文建立的格子Boltzmann 模型能够准确求解曲面边界的传热问题。

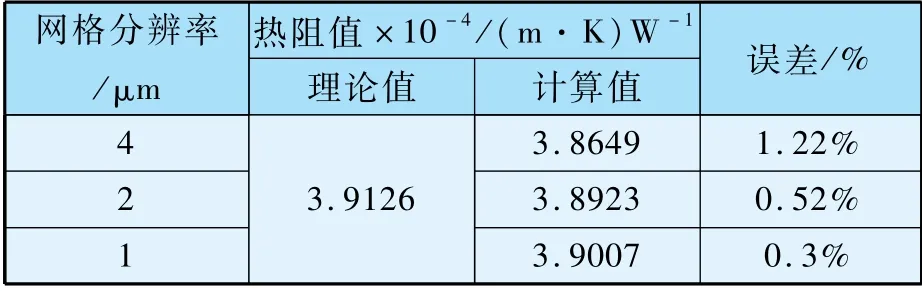
表1 理想光滑间隙下不同网格分辨率的计算模型准确性验证

与此同时，如表1 所示，随着网格分辨率的增加，计算误差越小。 因此，为了进一步验证实际模型中的网格无关性，本文对图1 中初始条件下（选取D=1.4，G=1.0 ×10-9，n =20 ～40 生成表面形貌）的粗糙表面下的接触热阻计算的网格无关性进行验证，固体材料为内外壁温分别为293 K和303 K的不锈钢圆环，其结果如表2 所示。

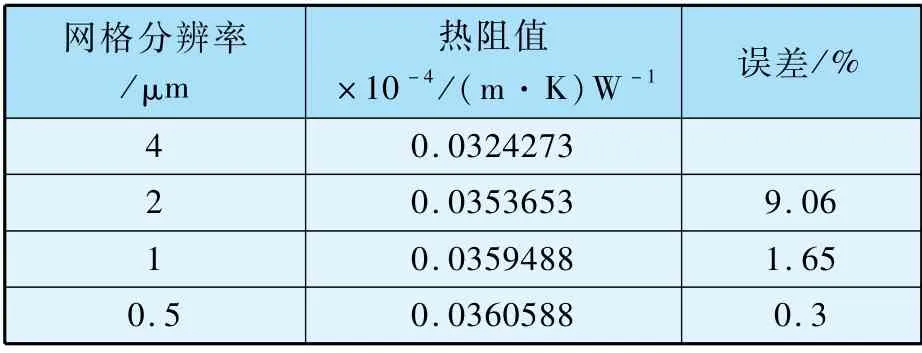
表2 分形形貌下网格分辨率测试

从表2 中可以看出，当网格分辨率从4 μm降低至2 μm时，接触热阻提高了9.06%。 而当分辨率从1 μm降低至0.5 μm时，热阻值仅提高0.3%。 网格对计算结构的影响可以忽略。 考虑计算效率，最优网格分辨率为1 μm。

3 结果与讨论

3.1 温度的影响

如图5 所示为，内外壁温分别为293 K和303 K不锈钢圆环，选取D=1.4，G=1.0 ×10-9，n =20 ～40生成粗糙接触面，在18.3 MPa压力下，稳态条件下得到的温度分布云图。 通过局部放大可以看出，在接触间隙附近存在较大的温度梯度。 这是由于间隙介质空气的导热系数远小于接触材料，是主要传热热阻，显著抑制接触界面间的传热。

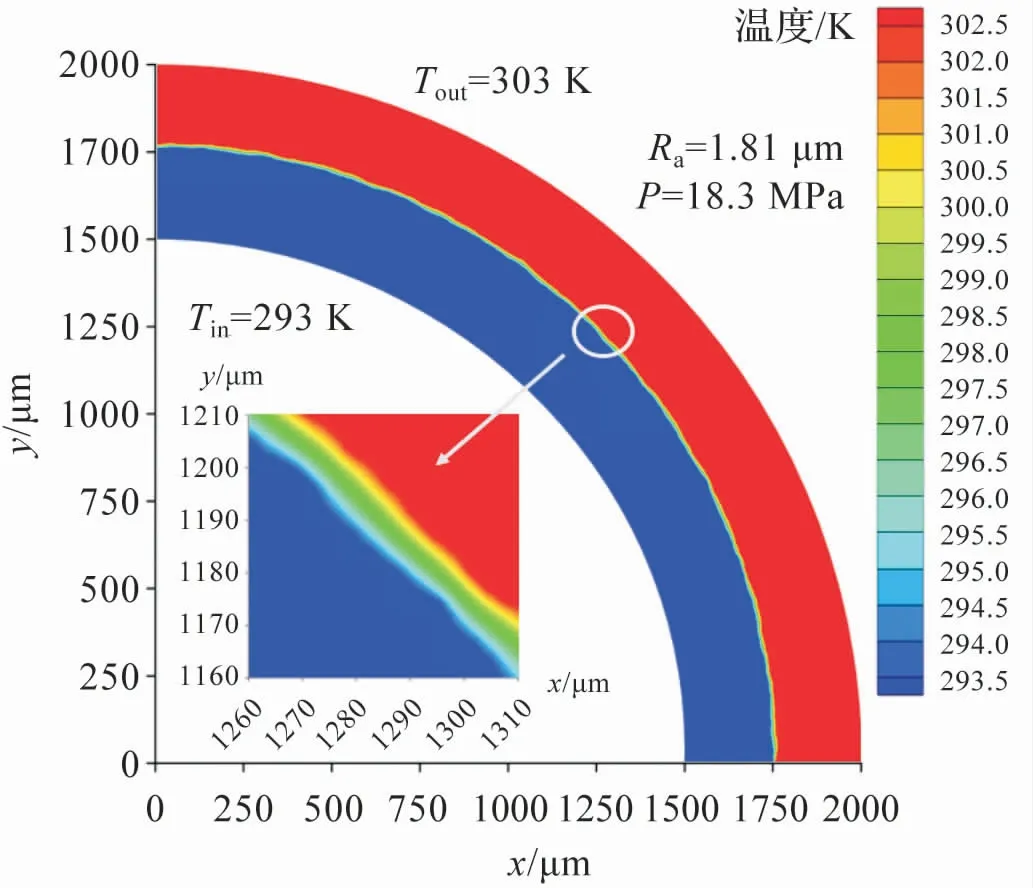
图5 接触热阻的温度分布云图

图6 为不锈钢接触热阻值随温度（上下壁面温度的平均值，其中上下壁面温差为10 K）的变化规律，接触热阻值单调降低，这是因为间隙介质空气的导热系数随着温度的升高而升高。

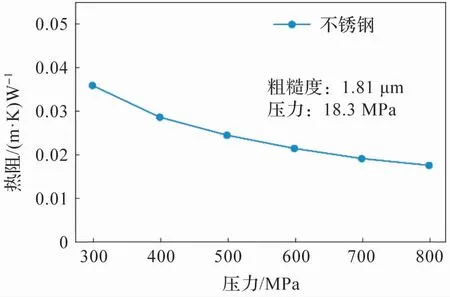
图6 接触热阻随温度的变化

上述模拟结果表明，接触界面区域的传热过程主要受间隙介质的导热系数抑制。

3.2 接触压力及接触材料的影响

如图7 所示，分别计算了铝和不锈钢两种固体材料环形曲面在特征粗糙度为1.81 μm（选取D=1.4，G=1.0 ×10-9，n =20 ～40 生成表面形貌）的具有分形特征的接触表面下接触热阻随压力的变化特征。 从图中可以看出，两种材料的接触热阻随压力的变化规律表现一致，即随着压力的增大接触热阻呈现出降低的趋势，且其降低速率逐渐趋于缓和。

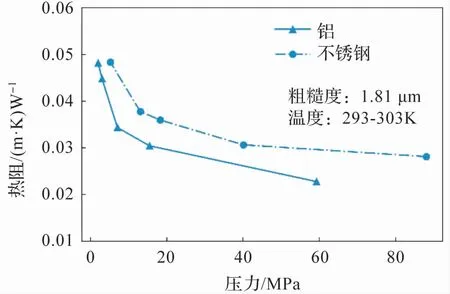
图7 接触热阻随压力的变化

为了进一步定量分析压力对接触面积影响，本文对不锈钢材料的接触面上间隙介质节点数随压力的变化特征进行了统计分析，其结果如表3所示。 当压力从0.8 MPa提高至13 MPa时，间隙介质点平均每兆帕减少898.52 个。 而压力从40 MPa提高到88 MPa，间隙介质点平均每兆帕减少57.29 个。 对应的，其接触面的接触特征如图8所示，可以看出间隙宽度随着压力升高明显减小。这表明随着接触面间的压力增加，微观接触面积会增加，且其增加速率会逐渐变小，压力对接触热阻的影响变得不再明显。 这一结果与平面下的结论较为一致[21]。 此外，由于不同材料的硬度特征不一样，导致在同一压力下其接触面积不一致，从而导致其接触热阻的绝对值上存在差异。 如图7所示，高硬度的不锈钢，在同样压力工况下，接触热阻略大于铝。

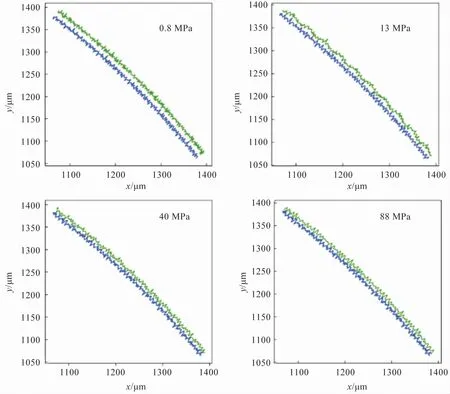
图8 不同压力下粗糙表面的接触情况

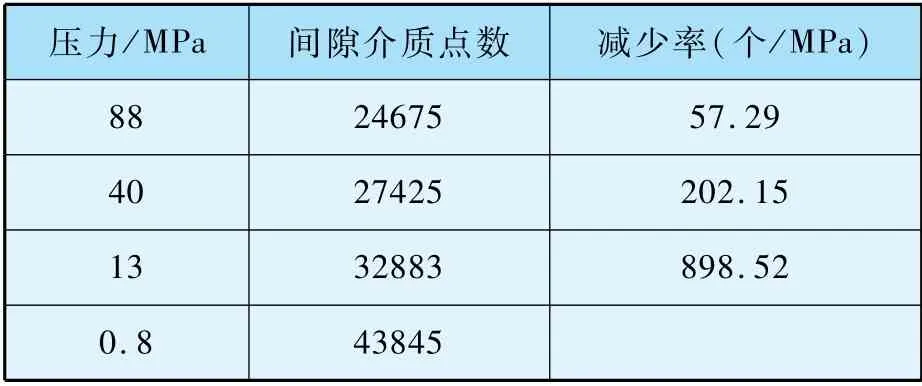
表3 不同压力下间隙介质厚度量化分析

3.3 表面粗糙度的影响

为研究表面粗糙度对曲面间接触热阻的影响规律，本文选取内外壁面温度为293 K与303 K，间隙介质为空气，接触材料为不锈钢，选取D=1.4，n =20 ～40 生成分形表面形貌，并通过改变分形特征尺度系数G来控制材料表面粗糙度，分别计算几种粗糙度下不同压力工况的接触热阻，具体模拟参数如表4 所示。

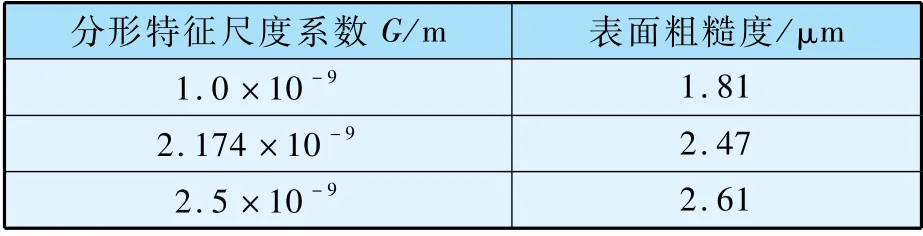
表4 分形特征尺度系数与表面粗糙度

接触热阻随表面粗糙度的变化规律如图9 所示。 对于三种不同形貌的表面，接触热阻均随压力的增加而降低，并且降低速率变小，这与3.2 节的模拟结果吻合。 与此同时，接触热阻值在各压力工况下，均随表面粗糙度的增加而增加，可见高表面粗糙度是接触热阻存在的重要原因。

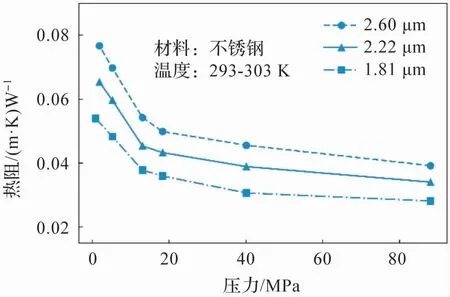
图9 粗糙度对接触热阻的影响

4 结 论

（1）本文提出一种基于格子Boltzmann 方法预测曲面间接触热阻的模型。 本模型使用曲面坐标作为W-M 函数的参数生成接触面分形形貌，使用塑性形变模型分析接触面的形变特征，使用插值方法处理曲面边界。 在计算有解析解的理想光滑曲面间隙热阻模型时，得到较为准确的计算结果。

（2）研究结果表明：不同影响因子主要通过改变接触面的间隙特征与间隙介质的导热系数最终影响接触热阻的大小。 其中温度主要影响间隙介质的导热系数，压力、材料和粗糙度影响接触面的接触特征。

（3）当间隙介质为空气时，接触热阻随温度的升高缓缓降低。 高压力，低硬度且表面光滑的材料，接触更充分，接触面间隙更小，其接触热阻往往更小。