基于BR-BP神经网络的页岩气集输管道冲蚀动态预测

何 跃 兰永福 樊 星 贾文龙 冷翔宇 吴 暇 黄 军 韩西成

（1. 中国石油集团西部钻探工程有限公司井下作业公司储存改造研究中心，新疆 克拉玛依 834099；2. 西南石油大学石油与天然气工程学院，四川 成都 610500；3. 汉正检测技术有限公司，四川 广汉 618399）

0 引言

北美“页岩气革命”的成功，给天然气能源的供给层面带去了巨大的改变[1]，我国以四川盆地埋深3500m内的海相页岩气区生产为主的全国页岩气生产也在2020年达到了200×108m3的产量[2]。

然而部分页岩气站的集输管道在生产过程中出现了腐蚀穿孔的现象，例如在我国川南页岩气开采生产过程中，某单井使用了4×104～5×104m3用量的水平井压裂液、2.5×103～3.0×103t用量的以石英砂和陶粒为主的支撑剂，这导致了压裂过程中的返排液会给页岩气集输管线带来不同程度的冲蚀腐蚀[3,4]，并且集输管道在开采及生产阶段还伴随有运行压力和流量的快速衰减，根据页岩气产量解析模型，页岩气生产满两年的实际压力流量平均递减率为56%[5]，其预测年递减率如图1所示，这使得冲蚀速率和冲蚀损伤程度也随时间不断变化，这些都对页岩气集输管道的长期安全生产产生了巨大威胁，所以建立管道壁厚受冲蚀减薄的动态预测模型对于页岩气集输管道的风险评价及预警具有十分重要的意义，而准确实时的集输管道冲蚀动态预测模型就显得尤为重要。

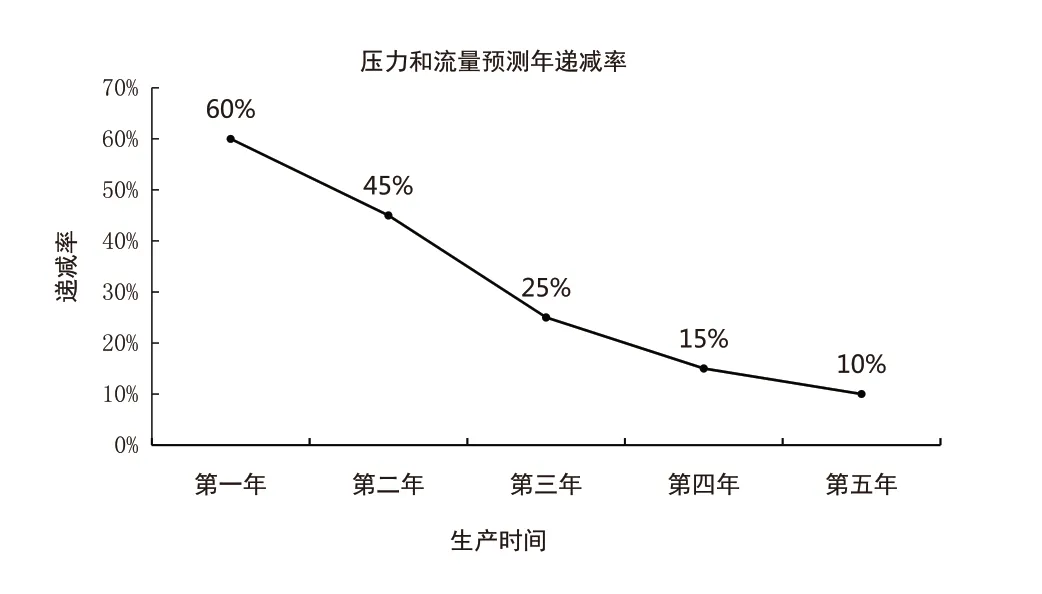
图1 压力年递减率分布

伍丽红等人[6]用BP神经网络进行了储层储量参数的确定和流体性质的判别，指出了用BP神经网络做出的快速分析是有意义的。2010年栾瑞鹏等[7]在建立钢材大气腐蚀影响因子的评估型时引入了贝叶斯正则化（BR）算法来解决小样本泛化问题。在2017年，Pandya等[8]将CFD和BP神经网络相结合，采用了遗传算法（GA）和贝叶斯正则化（BR）进行优化处理，将对油气管道弯头冲蚀速率的预测误差减小到了10%以下。到了2021年，Zhang Nan等人[9]基于贝叶斯规范化人工神经网络（BRANN）提出了深水钻井升井机脆弱性评估方法，证实了其有效性，但缺乏动态预测能力。但是BP神经网络在冲蚀预测的方面具有容易陷入局部极小值，泛化能力较差，需要提高学习速率和预测精度的缺陷[10]，目前少有学者将BP神经网络与贝叶斯正则化结合起来针对页岩气集输管道的特殊冲蚀情况建立预测模型。

本文将贝叶斯正则化方法与BP神经网络相结合，基于此建立了针对页岩气集输管道特殊冲蚀情况的动态预测模型，后续能够直接为页岩气集输管道的监测系统服务，改进神经网络解决传统BP神经网络的泛化推广能力差的问题，动态预测模型的求解解决了页岩气集输管道的压力变化问题，应用实例验证了在管件冲蚀方面的预测精度和有效性。

1 BR-BP神经网络

1.1 BP神经网络基本概念

BP神经网络（BPNN）是众多机器深度学习模型中一种常用的人工神经网络（ANN）预测模型，而ANN是一种被设计出来模仿生物神经系统的结构和功能的运算模型，能够自我组织、自我学习和自我适应，同时拥有很强的非线性映射能力，现在的学者多用其来解决一些分类问题和非线性问题[11]，还可利用其逼近非线性函数的功能应用到预测工作之中。

BPNN便是众多ANN中最典型的一种神经网络，其全称为误差反向传播多层前馈神经网络，现如今应用十分广泛。激励信号向前传递时产生的计算误差反向传播是BPNN最主要的特点，该模型概念是由Rumelhart等学者最先提出的，由三个主要部分组成模型的基本结构，其分别为输入层、隐含层和输出层，该模型的计算过程近似一种每层中都包含有许多计算神经元的网络结构，其神经网络结构如图2所示。

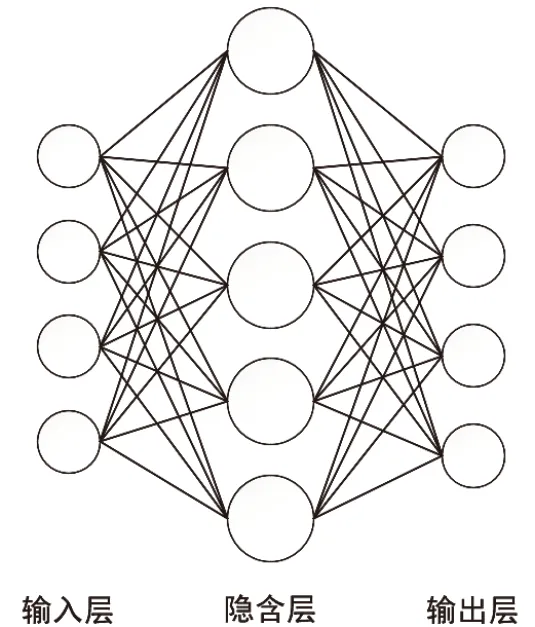
图2 BP神经网络结构

人工神经网络模型的基础是一个个用于计算的“神经元”，神经元是一种计算方式类似生物神经系统响应的拓扑结构。在BP神经网络的神经元中，其计算过程如图3所示，输入层的神经元负责接受所需要的输入分量Xi（i=1，2，3，···，n）即外部信号，然后通过权值Wi（i=1，2，3，···，n）连接传递到隐含层神经元，在加权求和后通过激活函数F处理非线性问题，再传递到输出层进行验证，得到的误差反向传递回隐含层进行再次学习，其中修正输出信号Z时会加入阈值λ，整个过程由训练函数进行调控重复多次，以达到误差不再下降或者最大迭代次数。

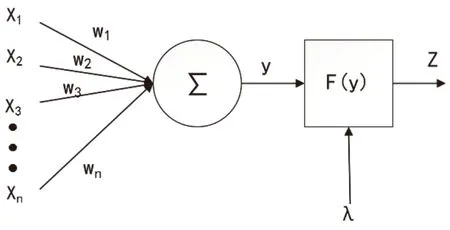
图3 神经元计算过程

其中激活函数即传递函数主要使用logsig函数和tansig函数[12]，分别如式（1）、（2）所示：

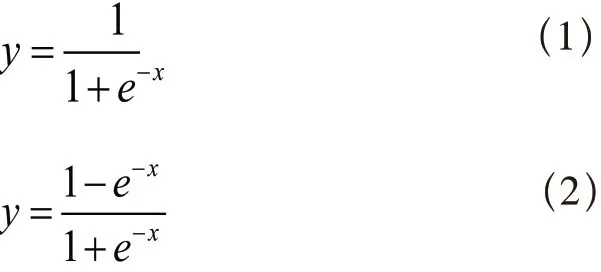
最常使用的是logsig函数即sigmoid函数，将logsig函数绘制出如图4所示。可看出该函数单调递增，符合生物学神经元的特点，输入信号越大，激活后输出信号越大，该函数的值域为（0,1），其作用就是把定义域（-∞，+∞）映射到（0,1）中，体现了激活函数将大范围的数限定至0～1的信号中继续传递的能力。

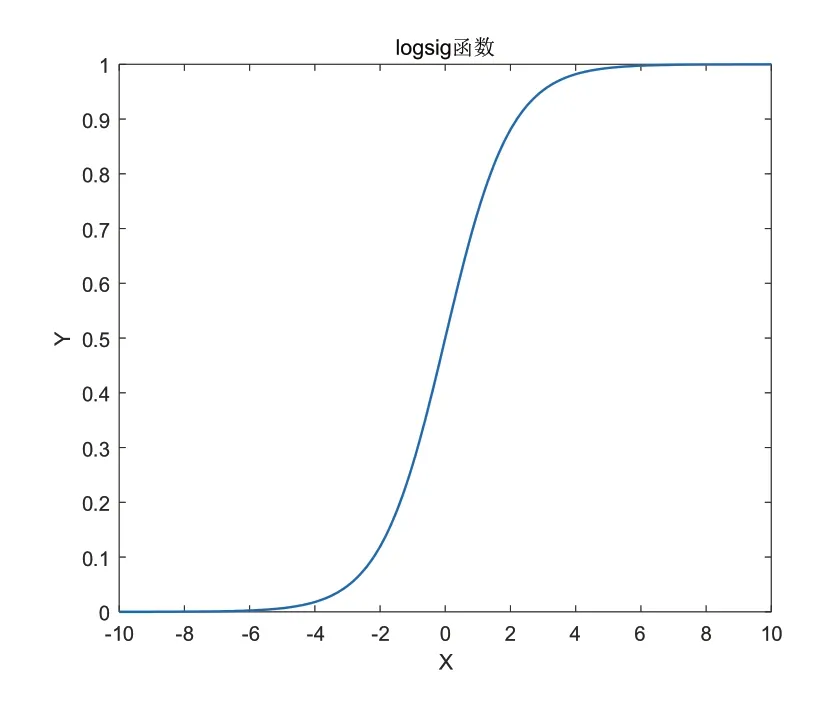
图4 logsig函数曲线

基于上述的神经元结构及激活函数，传统BP神经网络使用了梯度下降法作为学习方法，根据反向传递的误差来调整内部连接的权值和阈值，以完成使误差尽可能小的目标从而建立预测计算模型。

1.2 BR法训练

B R即为贝叶斯正则化（B a y e s i a n regularization）的简称，是基于贝叶斯定理发展而来的优化方法，即待求解的量可以通过先验概率的分布来对其进行描述，待有样本信息的加入后联合先验信息来进行判断[13]，贝叶斯定理的理论计算模型如式（3）所示。

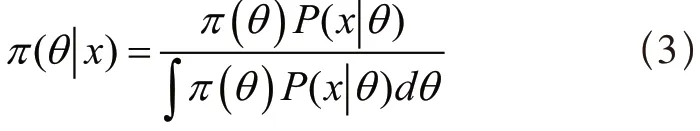
式中：θ为未知的待求量；x为样本；为后验信息分布；为先验信息分布；为未知样本时的先验概率即正则项；则为样本x的边缘分布，作为对贝叶斯公式进行正则化过程中的归一化因子，与待求量θ无关。其中后验信息分布可解释为由于样本x的加入对先验信息分布调整的结果。

在训练BP网络模型过程中，BPNN会利用性能函数分析模型输出的计算误差来进行自学习，所以BP神经网络的BR算法核心就是利用正则化训练函数trainbr对于一般BP神经网络使用的mse均方误差性能函数进行修正[14,15]即进行先验性约束，引入如式（4）所示的函数。

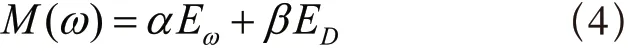
式中：M()ω为进行了先验约束修正后的性能函数；ED为神经网络训练输出结果的误差函数；Eω为神经网络训练过程中权值ω的误差函数；α、β均为BR法参数即超参数。

本文采用的trainbr函数其本质是通过对训练结果与目标的偏差来调整α、β，从而约束权值提升泛化能力，以达到最小化目标函数M()ω，从而来得到自适应的网络权值参数ω。

1.3 BR-BP神经网络的优势

贝叶斯定理的引入能够有效地优化神经网络模型，有助于解决具有不确定性的非线性问题[16]，而正则化的本质是约束要优化的参数，那么贝叶斯正则化其本质就是求解一个问题时，给其求解过程一个先验性约束或限制。

本文利用传统BPNN和BR-BP神经网络同时对一组由50个样本组成的天然气管道壁厚检测数据集进行学习时，在训练均方误差低于5并且验证和测试两种均方误差低于10时停止训练，而其他的参数条件均保持一致，每次训练人工神经网络完成时所耗费的时间如图5所示。

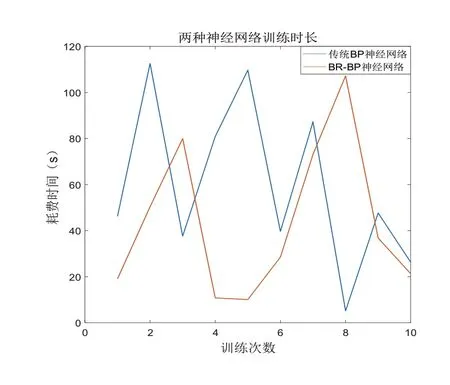
图5 训练次数与消耗时间的对比

我们可以发现BR-BP神经网络的训练时长低于传统的BP神经网络训练所需要的时间，相对来说BR-BP神经网络训练速度更快，这是因为传统BP神经网络使用的算法为梯度下降法，初始权值和阈值随机指定，而所需要拟合的最小化目标函数又往往比较复杂且为非线性的，那么训练过程必然比较低效[17]。

在进行初次训练时，传统BP神经网络初始化的权值和阈值均随机指定的，其范围很大，不同的方法训练出来的BP神经网络其性能也各不相同，这导致了网络的权值或阈值容易收敛到局部的极小点，即BP神经网络模型的训练陷入了局部极小化导致误差太大训练失败，所以初始权值和阈值的设定对于最终BP神经网络的训练结果有很大影响，BR-BP神经网络模型正是通过引入贝叶斯正则化的训练方法，对模型在训练计算时的初始权值和阈值进行了先验性约束，使得模型的权值和阈值在初始化后进行反复训练学习时不容易陷入局部极小值。

在此基础上再加入10组新样本作为两种神经网络的检验集进行预测时，对比分析50次训练后神经网络的预测值，计算后所得的模型预测结果相对误差曲线如图6所示。

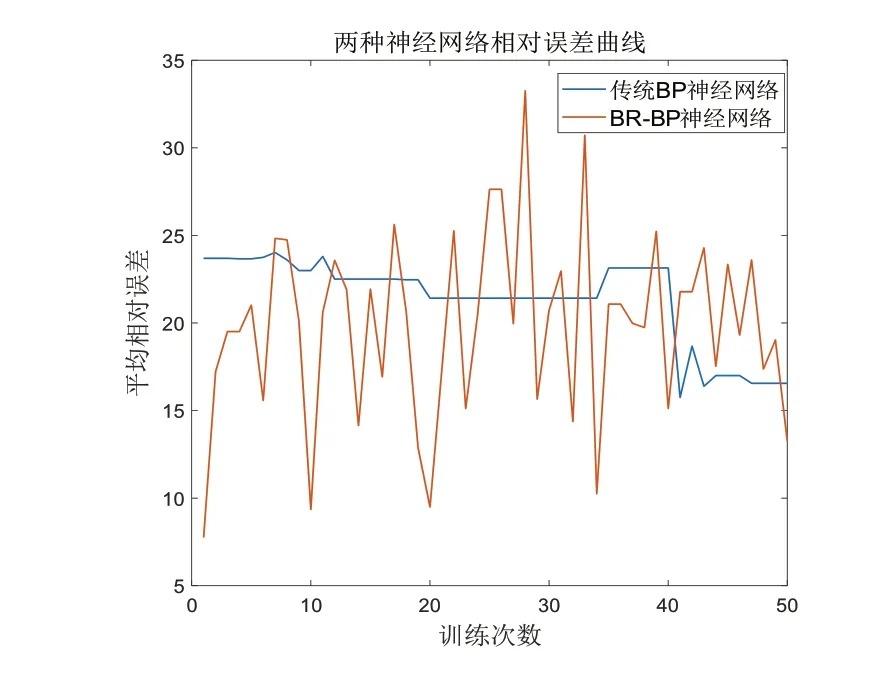
图6 平均相对误差曲线

从中可以看出传统的BP神经网络的预测相对误差的降低是一个缓慢过程，容易陷入局部极小值这一特点使得传统BP神经网络的误差曲线有较长的平缓段，而BR-BP神经网络在训练时的预测误差变化非常迅速，并且BR-BP神经网络的误差曲线几乎没有平缓段，这体现了其泛化能力的优势。

BP神经网络的预测能力即泛化能力取决于网络训练时的学习能力，但当网络在训练过程陷入局部极小值时，其泛化推广能力反而会大大下降，产生“过拟合”现象，所以传统BP神经网络的训练效果又会对网络的预测产生影响，为了避免产生“过拟合”，BR-BP神经网络利用贝叶斯正则化进行约束的方法便显得尤为重要，其增强了人工神经网络的泛化能力，从而提升网络的预测精度。

2 页岩气集输管道冲蚀动态预测模型

2.1 预测模型的输入输出参量设置

要利用BR-BP神经网络建立动态预测模型，则需要建立模型的输入参量，即壁厚减薄的影响因素。

针对长宁区块页岩气集输管道具有高压、高砂量和高液量的工作特点[4]，设定了运行时间、最高工作压力、平均工作压力、总含砂量、总含液量和施工工艺6个输入参量；页岩气田在不同的井区页岩气储层地质结构和开采深度不同，导致运行压力、含砂含液量也不尽相同，会进一步影响管道内介质的含砂量含液量，因此设置生产地区为另一个输入参量。在模型的输出方面，研究选择了管件壁厚这个容易在页岩气集输站场监测的数据作为，来作为衡量具体冲蚀情况预测的输出数值，更符合现场实际，有利于在编程成为预测软件结合监测系统帮助井区站场进行实时预测、风险分析与报警。

综上所述，根据相关输入输出参量建立了如图7所示的神经网络输入层和输出层。

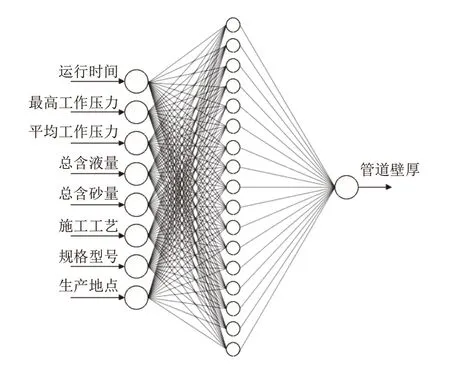
图7 输入层、输出层参数设置

2.2 基于BR-BP神经网络的预测模型建立

使用机器语言对BR-BP神经网络预测模型进行编程，因为Matlab软件的神经网络工具箱在训练神经网络时的重复训练非常麻烦，也无法直观的观察到训练出的神经网络预测值和相对误差，所以为了弥补这些缺陷并且完成预测模型的建立，本研究基于Matlab软件编写了使用trainbr函数训练BP神经网络的程序代码，该程序可以进行BR-BP神经网络的自动重复训练以及自动检验预测值，从而实现基于BR-BP神经网络预测模型建立，其程序流程框图如图8所示。

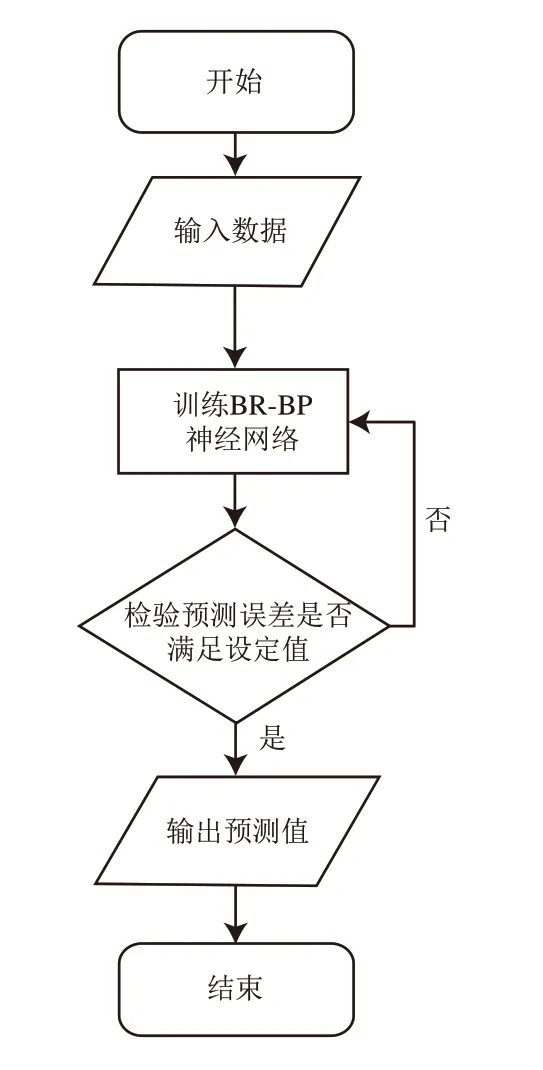
图8 预测程序流程框图

该基于BR-BP神经网络的预测程序运行时，以输入数据集中80%的数据组为样本对BP神经网络模型进行BR法训练，然后将数据集剩余的20%作为检验集，用训练好的BR-BP神经网络进行预测，将预测值与实际值相比较，判断误差是否达到设定值，若否则返回重新训练，若是则输出预测值结束程序。

2.3 动态预测模型的求解

为了适应页岩气集输管道的冲蚀特点，根据该动态变化的学习训练过程建立了动态预测模型的计算程序，其流程框图如图9所示，该动态预测模型的求解就是BR-BP神经网络预测模型参数的学习训练过程，其求解步骤如下：

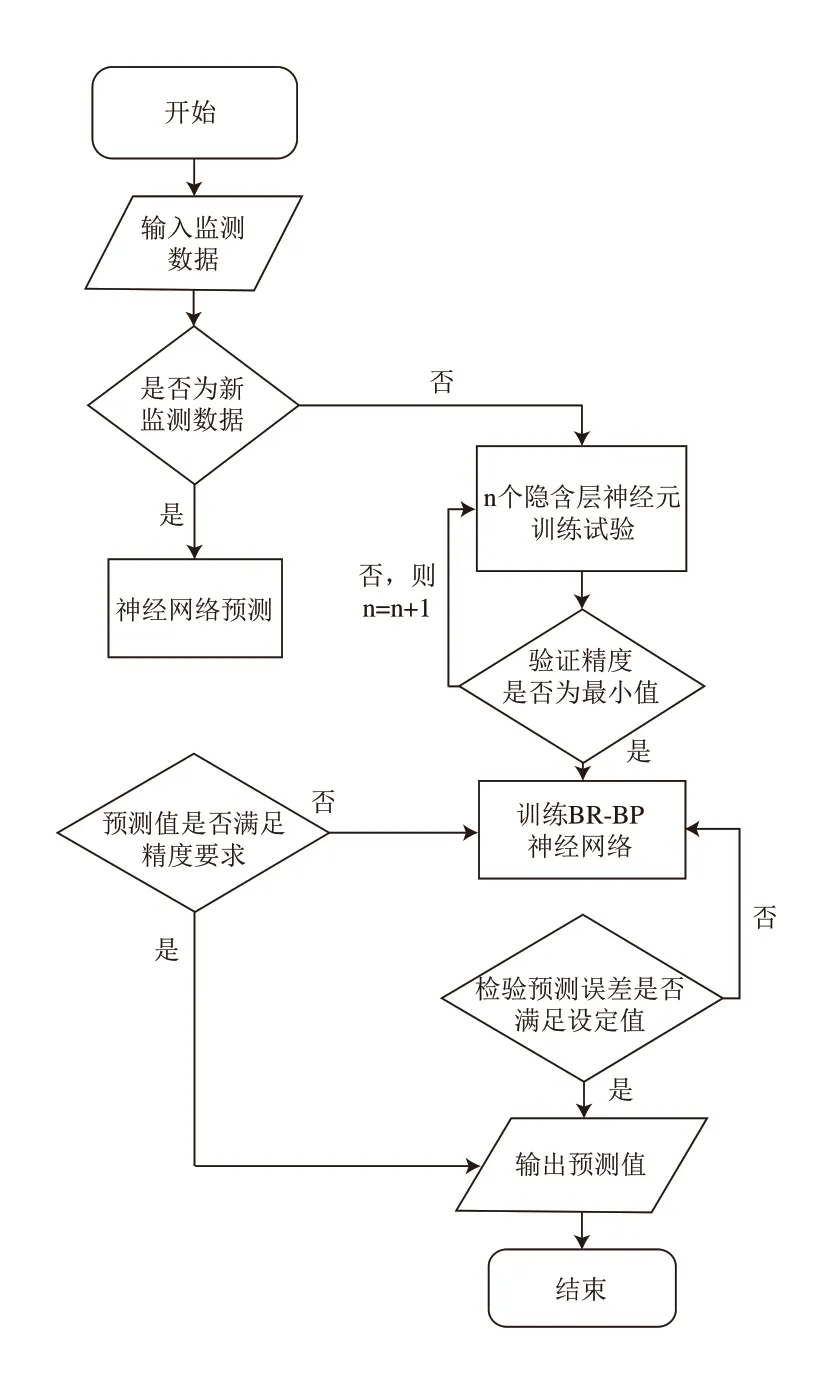
图9 动态预测模型求解流程框图

（1）输入页岩气集输管道监测数据，由于预测模型需要动态适应冲蚀情况的变化，所以采用现场的页岩气集输管道的监测数据作为神经网络的训练集和验证集，从而完成BR-BP神经网络的训练及预测；

（2）判断是否属于新监测数据，若是则进入预测计算，然后判断其预测精度，若满足要求则输出预测值结束程序，若不满足则重复训练网络直到预测精度达到设定值再输出新预测值；若不属于新监测数据则进行隐含层神经元个数试验，找到相匹配的个数后重置模型隐含层神经元数量，如今隐含层神经元个数缺乏固定有效的筛选手段[10]，所以针对不同的输入分量的隐含层神经元个数需要进行试验来选择最适合的个数；

（3）在隐含层神经元个数选择完后进入BR-BP神经网络的训练过程，每一次训练完成后通过预测值与实际值的误差对比来判断是否需要重复训练神经网络模型，在到达设定值之后输出预测值结束计算。

3 实例应用

本文使用Matlab软件将该BR-BP神经网络预测模型、传统BP神经网络和LM法训练的BP神经网络（后文简称BR-BPNN、传统BPNN和LM-BPNN）对于一个由3500组页岩气管道监测数据组成的样本进行学习训练，并且隐含层神经元个数经过训练试验择优后设定为17个，然后再对一组由30组数据组成的新加入样本进行管道壁厚的预测，各模型预测的壁厚值结果分别如图10所示，其相对误差如表1所示，本文组成样本的数据集主要取自威202、威204、长宁H24和长宁H25井区的集输管道监测数据。

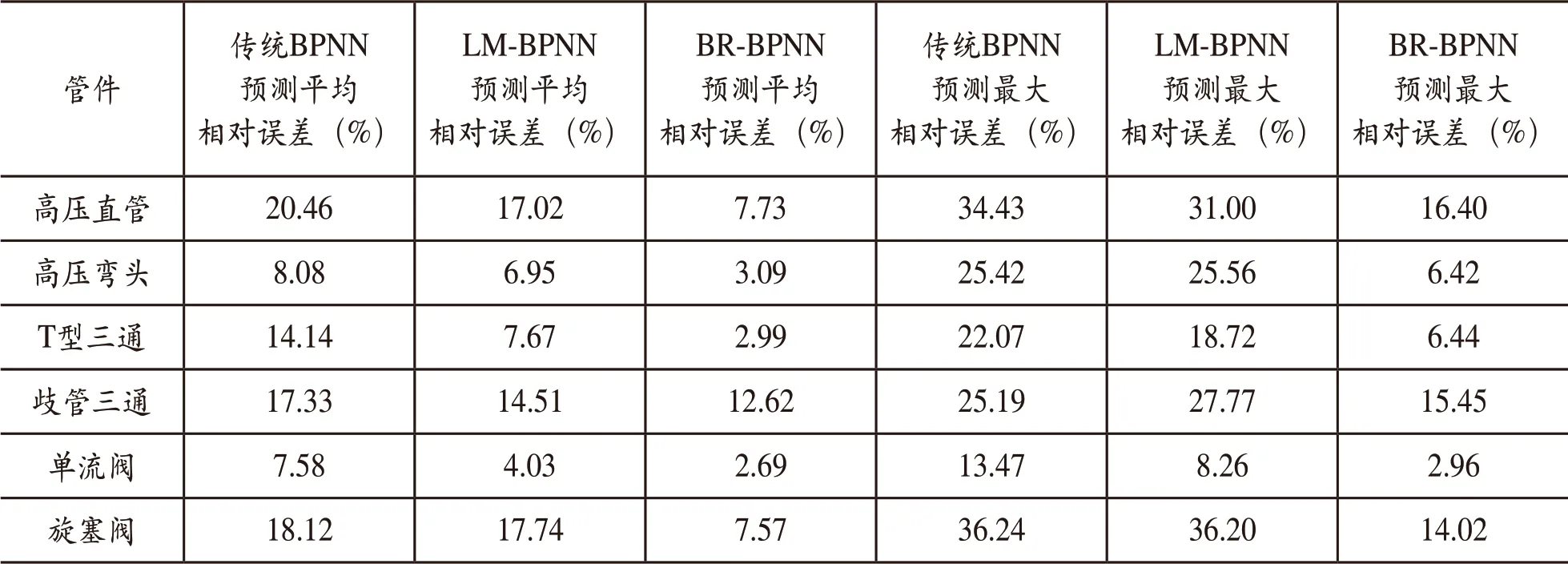
表1 壁厚预测值相对误差

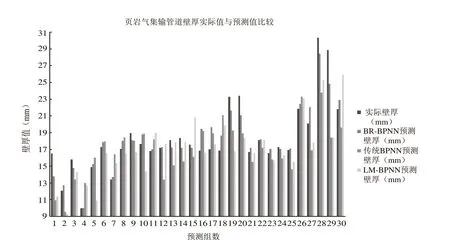
图10 页岩气集输管道壁厚实际值与预测值

通过对页岩气集输管道壁厚值进行预测的实例验证可以看出，本文经过改进后的神经网络预测模型对于页岩气集输管道的冲蚀预测比起传统方法更加准确，对比预测结果后发现，其预测的相对误差均有不同程度的减小且最小平均相对误差为2.69%，而且该预测模型的最大相对误差更小其最小值为2.96%、最大值为16.40%，更小的预测误差使得该动态预测模型拥有更加准确可靠的冲蚀预测能力，证明了该模型对于页岩气集输管道冲蚀情况进行动态预测的可行性。

4 结语

（1）针对容易“过拟合”的常规BP神经网络模型，用贝叶斯正则化方法来进行BP神经网络的学习训练，进而建立进行机器学习的神经网络预测模型，能够改善传统BP神经网络容易陷入局部极小值的状况，进一步增强动态预测模型的泛化推广能力；

（2）针对页岩气集输管道管壁受冲蚀减薄较快和压力流量的动态变化问题，基于BR-BP神经网络建立了壁厚动态预测模型，使预测模型能够根据新的页岩气集输管道监测数据进行动态化学习训练，从而实现了模型对于页岩气集输管道冲蚀情况的动态预测；

（3）通过实例验证可以得出，该预测模型的预测相对误差要明显小于传统BP神经网络和LM法训练的BP神经网络，证明该预测模型的精度得到了较大提升，进而使得针对页岩气集输管线的动态预测模型在实时学习训练时也能得到较为准确的预测值。