三维时空中两个不同实主曲率类时共形齐性曲面的分类

林燕斌

(闽南师范大学数学与统计学院，福建 漳州 363000)

定理1{θ1，θ2,θ3;W}是超曲面M3的一个完备Möbius不变量系统.

进而，证明了这一类Möbius齐性超曲面是常Möbius曲率的杜邦超曲面，并且Möbius等价于下面情况之一：一个是3中平坦环面在4中做锥，另一个是4中3个不同主曲率的等参超曲面.

1 类时曲面的不变量系统

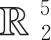
〈u,v〉=u1v1+u2v2+u3v3-u4v4-u5v5,

(1)

〈u,v〉1=u1v1+u2v2-u3v3.

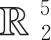
在活动标架{ei,n}下x的结构方程为

因此，

曲面x的Laplace算子为

△x=tr(S)n= (λ1+λ2)n,

曲面x的标准数量曲率为

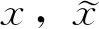
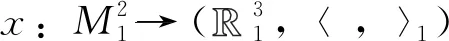
(1)标准共形不变度量

gc∶=(λ1-λ2)2g.

(2)共形不变曲率

W∶=1.

(3)典则提升

Y∶=(λ1-λ2)y,

(4)共形切标架

(5)典则法标架

ξ∶=λ1y+ξn,

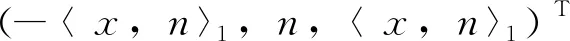
利用待定系数法，同样可以求得曲面在共形标架下的结构方程为

(2)

(3)

(4)

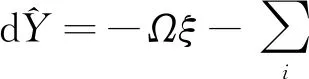
(5)

其中

故有(0,2)型张量分别为

并且将Ω称为共形形式，τ称为共形第二基本形式,Θ称为Blaschke张量和Ωij称为联络形式.

通过观察结构方程，可得如下定理:

根据Poincaré引理，可以求得曲面的可积条件为

(6)

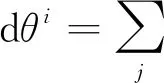
(7)

(8)

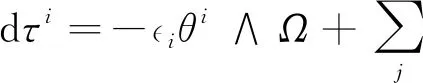
(9)

dΩij=jΘi∧θj+iθi∧Θj-τi∧τj,

(10)

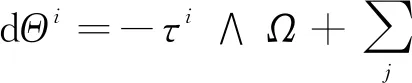
(11)

因此，可得如下定理:

证明 根据方程(9)得到

对比θi∧θj项的系数可知

由此说明，共形形式Ω由Ei，τ和Ωij决定.

根据方程(8)推出，对比θi∧θj项的系数可得

根据方程(10)推出

对比θi∧θj项的系数可得

由此说明Blaschke张量Θ由Ei、τ和Ωij决定.

利用Ei(ξn)=-λiEi(y)得知

(12)

与此同时

(13)

根据方程(3)推出

(14)

因此

计算可知

因此，该类曲面的李括号为

(15)

这说明联络形式Ω12可以由[E1,E2]完全决定.

综上所述，可得共形形式Ω、Blaschke张量Θ、 共形第二基本形式τ和联络形式Ωij，都可以由常数0、1和李括号[E1,E2]完全决定.

注1 利用定理4，最终可以通过计算李括号[Ei,Ej]是否相等，快速判断2个类时曲面是否全等．故只需要计算曲面的主曲率{λi}和主方向{ei}，然后就可以算得李括号[Ei,Ej]．如果2个曲面的[Ei,Ej]相同，则它们在允许相差一个共形变换下这2个曲面是全等的.

2 类时共形齐性曲面的例子

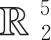
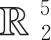
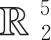
因为

S(ψ,φ)∘g∘ST(ψ,φ)=g，S(ψ,φ)∈O(3,2),

S(ψ1,φ1)∘S(ψ2,φ2)=S(ψ1+ψ2,φ1+φ2e-Aψ1),

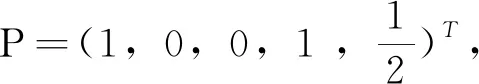
g=-(1-A2)e-2Aψ(dψ)2+(dφ)2.

x的单位法向量为

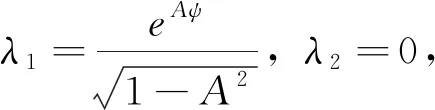
选择共形切标架为

因此，求得这类曲面对应的李括号为

[E1,E2]=-AE2，A∈(0,1).

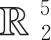
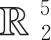
[E1,E2]=-AE2，A>1.

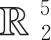
[E1,E2]=-AE1，A>0.

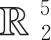
G(ψ,φ)=

3 类时共形齐性曲面的分类结果

已知共形齐性曲面和类时杜邦曲面的定义:

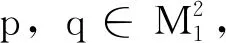
在此首先给出如下定理:

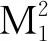
证明 利用方程(11)、(12)、(13)，则容易证明该定理成立.

最后，得到最重要的分类定理：

(1)洛伦兹平面上的双曲对数螺线，见例1、例3.

(2)洛伦兹平面上的对数曲线，见例2、例5.

(3)洛伦兹平面上的对数螺线，见例4.

证明 在下面的证明过程中分2种情形进行讨论.

情形1若在共形齐性曲面中Ω=0，则根据定理5可知，该类曲面共形等价于类时杜邦曲面.

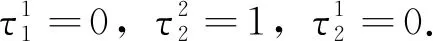
根据方程(6)和(8)比较θ1∧θ2项的系数可得,

根据结构方程求得这类曲面对应的李括号为

(16)

由方程(7)和(9)比较θ1∧θ2项的系数得出

再由方程(10)比较θ1∧θ2项的系数得出

(17)

根据主曲率取值不同，可以分以下3种情形进行讨论:

(1)当Ω1≠ 0,Ω2=0时,由方程(11)，比较θ1∧θ2项的系数得出

(18)

根据方程(17)和(18)，

由此可知结构方程中的所有系数由[E1,E2]=-Ω1E2唯一确定.

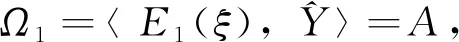
当0

当A=1时，这类曲面的李括号为[E1,E2]=-E2，根据定理4可知，该类曲面共形等价于洛伦兹平面上的对数曲线，见例2.

当A>1时，这类曲面的李括号为[E1,E2]=-AE2，根据定理4可知， 该类曲面共形等价于洛伦兹平面上的双曲对数螺线，见例3.

(2)当Ω1=0,Ω2≠ 0时，由方程(11)，比较θ1∧θ2项的系数得出

(19)

根据方程(17)和(19)

由此可知结构方程中的所有系数由[E1,E2]=-Ω2E1唯一确定.

(20)

根据方程(17)和(20),

综上所述,定理6证毕.