基于标定架的空间坐标三维组合测量坐标转换方法研究
唐钰,李丽娟,林雪竹,郭丽丽,詹睿
(长春理工大学 光电工程学院,长春 130022)
当前工业测量系统中对于航天有效载荷器件的姿态信息,绝大部分是通过对安装在部件上的立方镜的位姿测量来实现,对于立方镜的坐标系标定,主流方法是通过两台标定好的经纬仪对立方镜相邻两镜面自准直来确定立方镜两垂直面的法向量的姿态信息,再通过右手定则建立高精度立方镜的坐标系。然而对于自准直测量尺寸为20 mm×20 mm×20 mm的立方镜镜面,当前只能使用高精度的光学经纬仪准直测量,因此,在航天器的工业精密测量中光学经纬仪有着无可取代的地位。由于航天器的测量信息最终都要统一在航天器的基准坐标系下,因此每次组合测量任务都涉及到测量数据坐标转换的问题。
传统工业级组合测量系统坐标转换多采用公共点转换法,然而经纬仪基于空间角前方交会原理测点精度难以与激光跟踪仪、激光雷达等主流三坐标测量系统比拟。文献[1]提出了融合iGPS系统与经纬仪系统联合测量的标定板坐标转换方法,然而该标定板是平面结构,实际测量现场环境复杂,可达性不好。文献[2]设计的标准器固定在通用三角架上,可以调节三脚架的高度来配合经纬仪准直立方镜。文献[3]提出了原位校准装置和校准方法,为本论文提供了综合标定架的结构思路,基于此,本文提出基于综合标定架的激光雷达与经纬仪组合测量的坐标转换方法,并进行精度测试与分析,评估了综合标定架的优势。文献[4]属于标定板测量坐标系转换思路的鼻祖,提出了构建标准器的主要思路。
1 基于综合标定架的坐标转换原理
传统方法对于不同坐标系之间的转换,通常采用公共点转换。例如激光雷达测量系统和经纬仪测量系统之间只需测量一组相同的坐标点,就可以直接实现两组坐标系之间的转化。
然而,经纬仪测量系统需要测量人员人眼观测瞄准目标点,因此对于点坐标的测量精度普遍偏低,因此使用综合标定架作为媒介辅助测量,可以减少甚至避免经纬仪测量点坐标。
1.1 激光雷达系统空间点测量原理
激光雷达是基于球坐标系的一种测量系统,其通过轴角编码器来获得目标的方位角和俯仰角,通过获取标准光纤与被测距离返回的光线时间差来计算目标的距离。其合作目标为工具标准球,测量时工具球心的中点即为测量坐标点,图1为工具标准球的磁性基座,该基座还可以配合iGPS、激光跟踪仪等合作目标使用。

图1 工具标准球的磁性基座
图2为激光雷达测点原理图,被测点的计算公式为:

图2 激光雷达测点原理

式中,R为测量距离;θA为测量水平角;θE为测量俯仰角。最终得到被测点P的三维坐标。
1.2 经纬仪系统空间点测量原理
经纬仪属于无源定位系统,如图3为经纬仪的合作目标半球靶标,将经纬仪视准轴对准目标点即可获取目标点的水平角与俯仰角。因为只有角度信息,所以为获取目标的点位信息需要配合基准尺来约束距离条件,以获得目标空间三维点坐标。

图3 半球靶标
经纬仪测量空间点的坐标是基于空间测角度前方交会原理,如图4所示,A、B为两台经纬仪,空间待测点P(XP,YP,ZP),以经纬仪A为原点,经纬仪A与经纬仪B互瞄方向在大地的水平面上进行投影即为X轴,经纬仪A和大地的水平的垂直方向为Z轴,根据右手定则可以得到Y轴,来建立双经纬仪测量网络坐标系。

图4 空间前方交会原理
当已知基线长度b时被测点P的三维坐标计算公式为:

式中,αAl、αB1分别为经纬仪A、B瞄向测点P时的水平角;βA1、βB1分别为经纬仪A、B瞄向测点P时的竖直角;b为经纬仪A与经纬仪B的水平方向距离,通常称为基线。
当已知仪器在坐标系中的三维坐标时,被测点P的三维坐标计算公式为:

式中,αAl、αB1分别为经纬仪A、B瞄向测点P时的水平角;βA1、βB1分别为经纬仪A、B瞄向测点P时的竖直角。
1.3 经纬仪标定立方镜坐标系原理
待标定立方镜的坐标系主要根据立方镜几何中心及表面法线确定,立方镜几何中心作为坐标系原点,以其中两个相互垂直的表面法线确定其中两个坐标轴方向,右手定则确定第三轴。
如图5所示,用经纬仪T1和T2对立方镜的两个相互垂直的表面进行自准直测量,然后T1和T2进行互瞄,记录测量数据,利用公式可求得立方镜两个相互垂直表面的空间夹角α。

图5 立方镜建系示意图
设α1为T1在互瞄方向上的水平观测值,α2为T1在准直方向的水平观测值;α3为T2在互瞄方向上的水平观测值,α4为T2在准直方向的水平观测值;V1为T1在准直方向的垂直观测值,V2为T2在准直方向的垂直观测值。

其中,i1、j1、k1是 T1测得的准直方向向量在 X、Y、Z轴方向的投影。

1.4 布尔莎七参数坐标系转换原理
对于大尺寸航天器件,通常采用七参数坐标转换方法,利用公共点把测量坐标系中的坐标值精确度较高地转换到特征基准的坐标系下,以高精度计算出项目需求的位姿信息或形位误差。
设坐标系o-xyz中有一点P,其坐标值为p(x,y,z),另一坐标系O-XYZ中点P的坐标值为P(X,Y,Z),则根据布尔莎七参数坐标转换,前后两坐标值的关系为:

1.5 方向余弦姿态转换原理

2 基于标定板的坐标系转换方案
若使用更高精度的三坐标测量仪器标定好正四面体坐标系与三立方镜坐标系之间的关系,则可以依据几何图形的关系完成标定综合标定架的坐标系转换关系。权威机构标定好综合标定架后,经纬仪测量系统可通过测量待测立方镜位姿并创建待测立方镜坐标系与综合标定架立方镜坐标系的联系,激光雷达系统可通过测量特征基准点位坐标和正四面体点位坐标来建立综合标定架和特征基准点位坐标系之间的联系。
2.1 转换原理
该综合标定架经过高精度加工,6根基准杆采用铟钢材料制成,其膨胀系数为1.6×10-6℃,材料稳定性高,结构固连稳定[3]。如图6所示,在正四面体标定架上固定安置三枚立方镜,并在正四面体四个顶点位置固定4个磁性靶座,并在4个磁性靶座上放置4个1.5英寸的标准工具球。

图6 综合标定架结构示意图
综合标定架上的三个立方镜Q、M、N和四面体的位姿关系由更高精度的三坐标测量仪器标定完成,其位姿关系如表1、表2、表3所示,如图7所示P1、P2、P3、P4四个点位可以创建正四面体坐标系。以P1中心位置为原点,P1、P2连线为 X 轴,P1指向 P2为正;P1、P2、P3组成的平面法线指向P4点中心位置连线为Z轴,以右手定则确定Y轴建立正四面体坐标系。

图7 综合标定架坐标系关系示意图
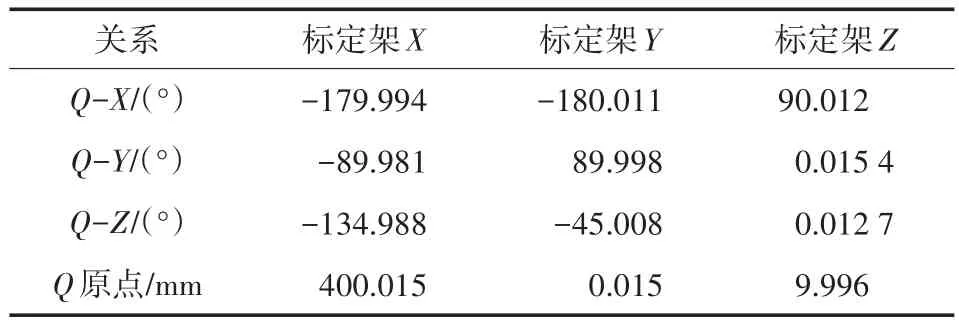
表1 正四面体与立方镜Q的关系

表2 正四面体与立方镜M的关系

表3 正四面体与立方镜N的关系
当使用激光雷达测量系统和经纬仪测量系统组合测量时,综合标定架可辅助转换坐标基准。
2.2 综合标定架方案的坐标系转换过程
(1)综合标定架上的立方镜坐标系与正四面体坐标系之间转换关系由权威标定机构提前标定 RPQ、RPM、RPN、TPQ、TPM、TPN,使用激光雷达测量正四面体的 4 个点位 P1、P2、P3、P4以及三个立方镜的中心点Q、M、N,根据式(13)求出校准测量时的综合标定架旋转矩阵RCPJ和平移矩阵TCPJ:

式中,P为正四面体4个顶点坐标;J为三个立方镜中心点坐标。
将校准求出的旋转矩阵与平移矩阵与权威机构标定的旋转矩阵与平移矩阵比较,误差满足测量任务要求即可,若不满足则需重新校准。
(2)使用激光雷达系统测量基准特征点,如图 8 所示。以 D1、D2两点连线为 X 轴,D3、D4两点连线为Y轴,D5为原点,通过右手定则建立基准特征点坐标系。
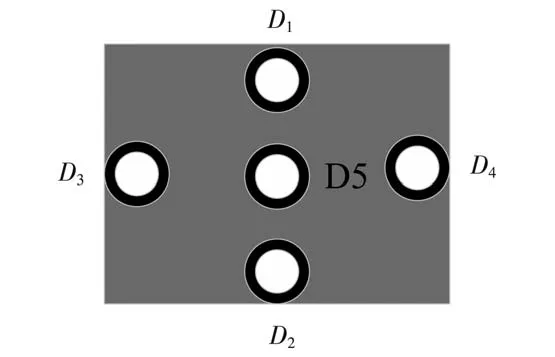
图8 基准特征点示意图
使用4台经纬仪系统组网建系,其中两台准直标定待测的立方镜J,得到J立方镜2个相邻面的法线以及立方镜中心点坐标,2个相邻法线以确定X轴与Y轴,再通过右手定则确定Z轴,从而建立J立方镜的坐标系。
(3)使用另外两台经纬仪分3次准直综合标定架上Q、M、N立方镜,建系方法同J立方镜,得到Q、M、N立方镜的坐标系。
(4)建立好以上坐标系即可通过坐标转换将所有坐标系统一在基准特征坐标系下,如图9所示。
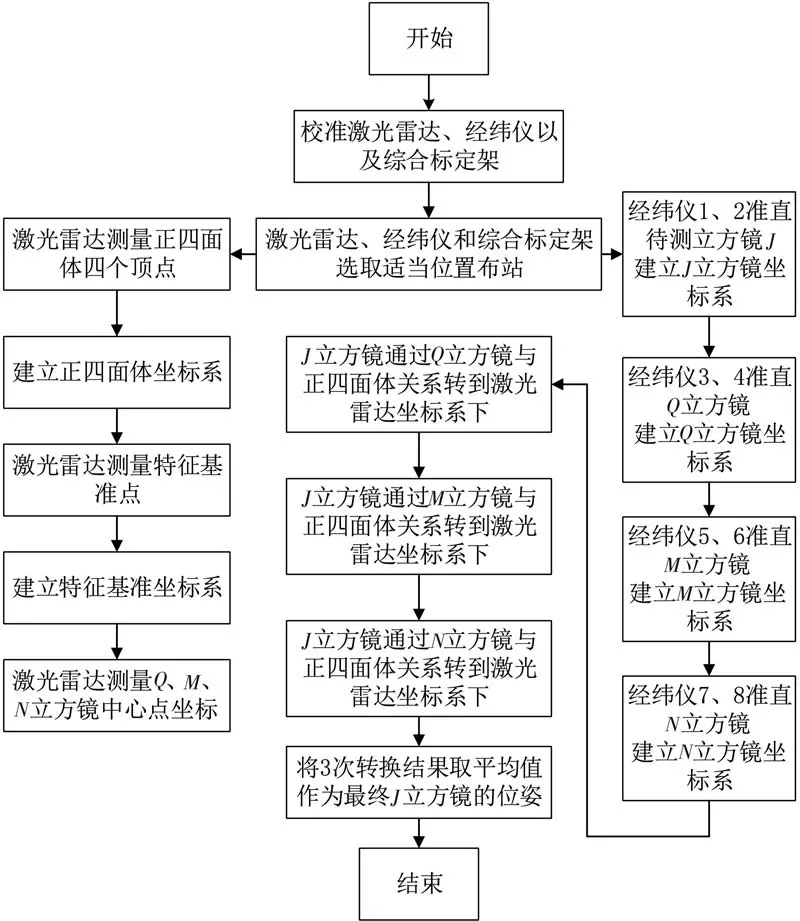
图9 综合标定架方案流程图
(5)最终,即可将待测立方镜J位姿转换到综合标定架的Q、M、N坐标系上,通过坐标配准原理[4]寻求一个最优值。最终可将待测立方镜J的位姿信息,转到基准特征坐标系下,从而实现组合测量坐标统一在同一坐标系下,如图10和图11所示。

图10 坐标转换示意图
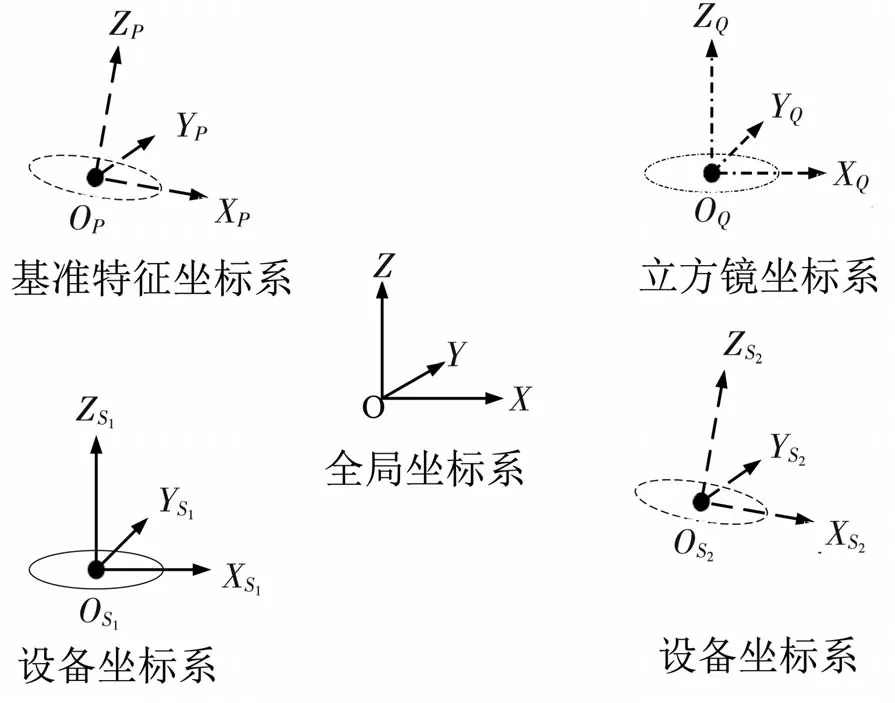
图11 标定解算坐标系示意图
3 实验验证
在标准气压室温20℃、长15m、宽10m的实验室内布设四台经纬仪进行组网建系,在两台经纬仪与激光雷达测量可达的位置随机且分散固定4~15个磁性基座,为确保实验的数据精度准确,测量过程中应确保通用磁性基座用胶枪粘结牢固,多次重复测量求取平均值以减小误差。软件选用SA(SpatialAnalyzer)软件和解放军信息工程大学研发的MetroIn工业测量系统软件。
3.1 传统公共点坐标转换
(1)激光雷达系统对模拟特征基准点进行点位测量,建立特征基准坐标系。
(2)使用两台经纬仪标定待测立方镜J1,建立立方镜J1坐标系。
(3)在2台经纬仪与激光雷达测量可达的位置随机固定4~15个磁性基座,分别用经纬仪测量系统和激光雷达测量所有磁性基座点坐标值,通过坐标配准原理[4]求解两套测量系统的坐标系转换参数 Rc、Tc。
(4)有了以上转换参数选取 7、10、12、15个点做坐标配准转换[4]并计算转换精度,同时计算这些测试点转换到经纬仪坐标系下的坐标值与经纬仪实测值的坐标差,结果如表4所示。

表4 公共点坐标转换精度测量实验结果
从表4可知,传统公共点转换法激光雷达系统与经纬仪测量系统转换精度在使用7个公共点时精度最高为0.176 mm,但点位平均差值大,说明此时公共点测量的可靠性较差,随着公共点数量增加到12个,精度接近维持在0.3 mm趋于稳定,可靠性稍好。在有公共点可测量的情况下传统公共点转换的原理简单,转换过程方便,但经纬仪测量系统人工干预较大,且两位经纬仪测量人员很难准确对准半球中心同一点位,导致测点精度不高,因此对于经纬仪这种无源定位系统转换精度较大,应当多加练习,且必须多次测量以获取可靠的点位坐标。此外,公共点布设位置必须保证所有参与转换的仪器同时观测到,公共点的数量和布设图形结构也会影响测量精度,因此还要调整公共点的数量和布局,才能有效保证坐标的转换精度。
3.2 综合标定架坐标转换
选取经纬仪1、2分别准直待测立方镜J1相邻两垂直面,得到立方镜J1的X轴和Y轴法线,通过右手定则建立J1坐标系;经纬仪3、4准直立方镜Q,建立Q坐标系;经纬仪5、6准直立方镜M,建立M坐标系;经纬仪7、8准直立方镜N,建立N坐标系,利用激光雷达系统测量特征基准坐标 D1、D2、D3、D4、D5点以及 P1、P2、P3、P4、Q、M、N点坐标,测量时应保持测量系统稳定。通过SA软件计算激光雷达与正四面体坐标系关系,如表5所示,同样使用SA软件计算,如图12所示,经纬仪与立方镜坐标系的转换关系。

图12 标定坐标系示意图

表5 激光雷达测量系统坐标系与正四面体坐标系的关系
最终测量结果的数据如表6所示,三次立方镜转换均值为0.152 2 mm,公共点转换均值为0.361 7 mm,即通过综合标定架方案完成激光雷达系统与经纬仪测量系统的坐标转换比传统公共点转换法提高了0.209 5 mm的转换精度。因为该方法中影响精度的因素只有激光雷达系统对正四面体点位的测量误差和经纬仪系统准直立方镜测量的误差,减少了经纬仪直接测量多个公共点坐标由人员误差导致的影响,而且三个立方镜多次测量也一定程度地减少了随机误差,从而达到降低精度的效果。

表6 经纬仪测量系统转换后的点位差值
4 结论
本文提出了利用综合标定架进行经纬仪和激光雷达组合测量的坐标系转换的方法,标定架具体制作标定过程,给出了综合标定架的具体模型,介绍了激光雷达测点原理,也介绍了经纬仪测点原理,和经纬仪准直立方镜的原理,以及各部分坐标系的建立过程和原理,还论述了两种实现组合测量坐标系转换的原理和过程,讨论了两种转换方法的具体的实验方案、实验方法、实验结果对比。实验最终表明,公共点转换方案虽然操作简单,而且方法可行,但在实际测量时,高精度的三维测量系统与无源定位系统组合测量时由于无源定位系统测点精度不高导致误差增大,因此具有一定局限性;而综合标定架方案则可以减少经纬仪对过多公共点测量的过程,利用已知的正四面体与立方镜的转换关系,通过准直立方镜来实现坐标系的转换,通过实验证明有效提高了两套系统组合测量的0.209 5 mm的转换精度,而且工业测量时基准坐标点被遮挡的情况下综合标定架可以辅助转移坐标系,目前标定架的相关研究较少,本论文为未来基于综合标定架的工业测量项目提供了一个可行的思路。

