钨/石墨烷/钨第一壁材料缺陷与力学性能的第一性原理计算

郭 顺, 张兆春, 谢耀平, 郭海波

(上海大学材料科学与工程学院, 上海 200444)

聚变能是解决未来人类能源问题的最有效途径. 托卡马克是实现可控热核聚变的主要装置之一[1]. 在托卡马克装置的真空室中, 直接面对等离子体的材料被称为第一壁材料[2]. 钨金属具有高熔点、高热导率、低溅射率等特点, 已作为第一壁材料被广泛使用[3]. 等离子体在放电过程中, 将有高通量高能粒子流沉积于第一壁材料, 导致材料产生辐照损伤和结构缺陷, 例如空位、自填隙原子、氦泡等. 这些结构缺陷会改变钨金属的微观结构和机械性能, 使材料出现脆化和肿胀, 从而影响托卡马克装置的稳定运行[4]. 所以, 提高钨金属的抗辐照能力和减少氦泡的密度成为第一壁材料研究领域的热点问题. 复合材料中的各种界面可以在一定程度上抑制辐射缺陷的形成和扩散, 从而增强基体的抗辐照能力. 根据一些实验结果和材料设计理论, 已有研究者设计将金属复合材料作为第一壁材料, 例如Cu/Nb[5]、W/V[6]. 然而, 由于边界热阻较高, 二组分金属复合材料的导热率比单组分金属材料低, 从而降低了第一壁材料的传热效率. 石墨烷是石墨烯的重要衍生物, 有着优良的导热性能, 于是本工作首次设计将钨/石墨烷/钨体系作为第一壁材料, 并使用第一性原理和准简谐德拜模型研究钨/石墨烷/钨第一壁材料对缺陷形成、力学性能和热力学性质的影响.

1 计算模型

在建立钨/石墨烷/钨第一壁材料模型前, 首先构建钨表面模型, 并通过计算体系的表面能确定最稳定的钨表面结构. 根据“晶格匹配度”和“最大配位数”原理, 构造各种钨/石墨烷/钨第一壁材料的初始结构, 通过计算这些结构的界面结合能, 来确定最稳定的钨/石墨烷/钨第一壁材料的结构模型. 在稳定的结构基础上, 使用第一性原理和准简谐德拜模型研究钨/石墨烷/钨第一壁材料的缺陷形成能、力学性能和热力学性质. 本工作采用基于密度泛函理论的维也纳从头算模拟软件包(Vienna ab-initio simulation package, VASP)进行第一性原理计算[7]. 交换关联泛函采用广义梯度近似中的Perdew-Burke-Ernzerh方法进行描述, 电子与离子间的相互作用采用投影缀加波(projector augmented wave, PAW)方法描述[8-9]. 在计算过程中所有原子都进行充分驰豫, 收敛判据为每原子的受力小于0.2 eV/nm, 电子自洽能量差小于1×10-6eV.

1.1 钨表面结构模型

W(110)、W(001)、W(111)3 个低指数面的表面模型如图1 所示. 在建模过程中使用周期性边界条件, 模型原子层数均设置为7 层, 且Z方向上真空层的厚度为1.5 nm[10].

图1 W(001)、W(110)、W(111)的表面模型Fig.1 Slab models of W(001), W(110) and W(111)

对上述3 个表面结构进行弛豫以达到能量最低状态, 计算过程中平面波截断能为350 eV,布里渊区采样使用Monkhorst-Pack 方法[11],k点密度为10×10×1, 表面能计算公式[12]为

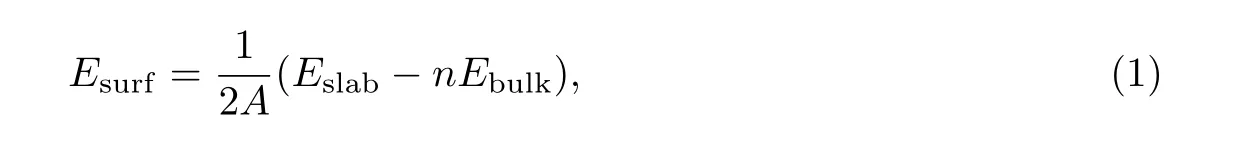
式中:Eslab是3 个表面结构优化后的总基态能量;n是表面超胞的总原子数;Ebulk是单个钨原子的基态能量;A表示表面积. 表1 是表面能和费米能级处的态密度计算结果, 在态密度的计算过程中,k点密度增加为16×16×1.

表1 W(110), W(001), W(111)的表面能和费米能级处的态密度Table 1 Surface energy and density of states at the Fermi level of W(110), W(001), W(111)

由表1 可知, W(110)面的表面能最低, 这意味着W(110)面是3 个表面中最稳定的表面.通过比较3 个面在费米能级处的态密度值N(EF)也能得到同样的结论. 费米能级处的态密度越小, 表面越稳定. 在3 个低指数晶面中, W(110)具有最小的N(EF)值(5.12). 态密度和表面能计算结果都表明W(110)面最稳定. 因此, 本工作选择W(110)面来构建钨/石墨烷/钨第一壁材料的模型.

1.2 钨/石墨烷/钨第一壁材料的结构模型

石墨烷(graphane)是石墨烯的重要二维衍生, 主要有两种构型: 一种是椅式结构(chair)(见图2(a)), 是在石墨烯的每个碳原子上都吸附一个氢原子, 而相邻的碳原子是上下交替吸附氢原子, 该构型是比较稳定的结构; 另一种是船式结构(boat)(见图2(b)), 是在石墨烯的每对碳原子上成对吸附氢原子, 但由于两个氢原子之间存在斥力, 导致这种构型不太稳定[13]. 石墨烷是一种全氢化的石墨烯, 碳氢计量比为1∶1, 其理想结构的分子式为(C1H1)n. 氢原子的吸附虽没破坏原石墨烯的二维构型, 但使其中碳原子的杂化类型由sp2转化为sp3, 形成的不再是平面构型的六角网络, 而是呈现了一定的起伏度. 石墨烷的C—C 键长也由石墨烯的0.142 nm转变成0.152～0.156 nm[14]. 石墨烷从船式结构变化到椅式结构需要氢原子在平面之间切换位置, 因此这种转变是极难发生的. 所以, 在建立钨/石墨烷/钨体系模型时, 本工作选择更加稳定的椅式石墨烷.

图2 石墨烷构象俯视图和侧视图(碳原子为黑色, 氢原子为绿色)Fig.2 Top and side views of the graphane (carbon atoms are black, hydrogen atoms are green)

钨晶体为体心立方结构, 空间群为P1 mm, 晶格常数为0.316 5 nm,γ为90°. 构造钨/石墨烷/钨第一壁材料模型时, 两相晶格失配度必须小于5%. 晶格失配度的计算公式[15]为

式中:A是界面重叠区域;AGR和ATi分别是构成界面的两相晶体表面层的面积. 为了使晶格失配度小于5%, 本工作选用2×5 石墨烷超胞和3×1 W(110)表面超胞. 考虑到计算精度和效率, 将钨/石墨烷/钨第一壁材料的模型原子层数设置为11 层(中间为单层石墨烷, 上方和下方各为5 个钨原子层), 界面间距为0.2 nm, 原子数量为112. 本工作考虑了3 种钨/石墨烷/钨第一壁材料模型: 第一种是钨原子占据碳原子的顶部; 第二种是钨原子占据碳六元环的中心;第三种是钨原子占据两个相邻氢原子连线的中点, 3 种结构模型如图3 所示. 3 种模型的界面结合能[16]为

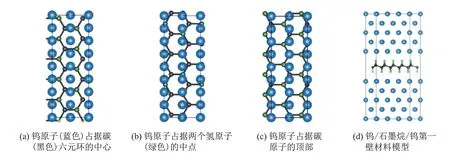
图3 3 种钨/石墨烷/钨体系结构Fig.3 Three tungsten/graphane/tungsten system structure

式中:Egraphane是钨/石墨烷/钨第一壁材料中石墨烷的基态能量;Emetal是钨金属的基态能量;Einterface是整个钨/石墨烷/钨模型驰豫之后的基态能量. 界面结合能的计算结果如表2 所示, 当钨原子占据碳六元环中心时, 界面结合能最大, 表明此结构模型较其他两种更加稳定.

表2 3 种钨/石墨烷/钨体系的界面结合能Table 2 Interface binding energy of three tungsten/graphane/tungsten system

2 结果与讨论

2.1 电子结构

Bader 电荷有助于研究石墨烷和钨原子之间的相互作用. 表3 列出了钨原子、碳原子、氢原子的平均Bader 电荷和平均Bader 体积. 可见, 钨原子平均Bader 电荷为5.994 3 e, 碳原子的平均Bader 电荷为4.004 8 e, 氢原子的平均Bader 电荷为1.015 6 e. 而第一性原理计算过程中W、C、H 的价电子数分别为6、4、1. 由此可知, 钨原子和碳原子、氢原子之间仅存在极少比例的电子离域现象. 在椅式构象的石墨烷中, 平均每个原子的结合能为6.56 eV/atom,这比其他C∶H 为1∶1 的碳氢化合物如苯(6.49 eV/atom)和乙炔(5.90 eV/atom)更高[17]. 在这样的碳氢组成比例下, 椅式石墨烷是已知的最稳定的化合物[13,18]. 因此, 钨原子和碳原子、氢原子之间的相互作用较弱. 从电荷密度图中也可以得到同样的结论, 图4 是钨/石墨烷/钨体系的总电荷密度图. 由图可见, 石墨烷的电荷密度和钨原子的电荷密度没有明显的融合.

图4 钨/石墨烷/钨材料的总电荷密度(蓝色是钨原子电荷密度, 红色是石墨烷电荷密度)Fig.4 Total charge density of tungsten/graphane/tungsten materials (the blue region is the charge density of the tungsten atoms, and the red region is the charge density of the graphane)

表3 钨/石墨烷/钨第一壁材料的平均Bader 电荷和平均Bader 体积Table 3 Average Bader charge and average Bader volume of tungsten/graphane/tungsten as first wall material

Parr 和Yang 在1984 年提出的福井函数是概念密度泛函框架中的一个重要概念, 已被广泛用于预测反应位点[19]. 通常, 福井函数值越大, 相应位点的反应活性越强. 由于本工作计算的是两相界面的福井函数值, 所以采用简缩福井函数来预测反应活性位点. 简缩福井函数的近似计算公式[20-21]为

在本工作模型中选取石墨烷层为参考系, 最靠近石墨烷层的位置为第一最近邻(first nearest neighbor, 1NN), 由内向外依次为第一最近邻、第二最近邻(second nearest neighbor,2NN)、第三最近邻(third nearest neighbor,3NN)、第四最近邻(fourth nearest neighbor,4NN)、第五最近邻(fifth nearest neighbor, 5NN). 由表4 可以看出, 第一最近邻钨原子层的福井函数值均高于第二最近邻钨原子层, 这表明石墨烷层附近的钨原子更容易受到自由基的“攻击”, 即越靠近石墨烷层的钨原子活性越强.

表4 第一最近邻和第二最近邻福井函数的平均值Table 4 Average value of the Fukui function of the first nearest neighbor and second nearest neighbor

2.2 石墨烷在抑制缺陷中的作用

聚变产生的氦原子很容易进入钨金属内, 聚集之后形成“氦气泡”, 这将导致第一壁材料出现肿胀和起泡. 本工作使用第一性原理研究氦原子在钨/石墨烷/钨第一壁材料中的形成能. 对于氦原子的间隙位置, 由于在体相中氦原子更倾向于占据四面体间隙位置, 所以优先考虑氦原子占据在四面体间隙位置(tetrahedral interstitial site, TIS). 氦原子形成能定义[22]为

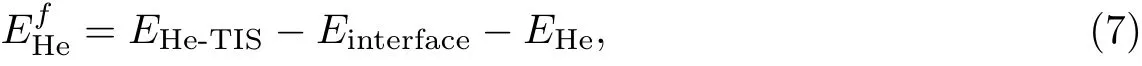
式中:EHe-TIS是只有一个间隙氦原子的钨/石墨烷/钨体系驰豫后的能量;Einterface是没有缺陷的钨/石墨烷/钨体系驰豫后的能量;EHe是单个氦原子的能量. 计算结果如图5 所示.

由图5 可以看出, 氦原子在第一最近邻钨原子层中的形成能远小于第二最近邻钨原子层和第三最近邻钨原子层中的形成能. 这表明在钨/石墨烷/钨第一壁材料中氦原子更倾向于占据在界面处, 或者是界面具有捕获氦原子的作用. 图6 展示了氦原子占据四面体间隙位置驰豫前后的情况. 由图6 可以看出, 氦原子无论是占据在第一最近邻还是第二最近邻位置, 弛豫后氦原子更倾向于移动到界面处, 这也再次验证了界面对填隙氦原子的捕获作用. 钨/石墨烷/钨第一壁材料中的界面有助于降低钨体相中氦缺陷的密度.

图5 氦原子占据四面体间隙位置的形成能Fig.5 Formation energy when helium atoms occupy tetrahedral interstitial site

图6 氦原子占据四面体间隙位置时驰豫前后对比Fig.6 Comparison before and after relaxation when helium atom occupy the tetrahedral gap position

为研究钨/石墨烷/钨第一壁材料对钨空位形成的影响, 使用下式计算钨空位形成能, 空位模型是通过移除第一最近邻层、第二最近邻层和第三最近邻层中的一个钨原子形成的[23],

式中:E(n-1)W+V、EnW、E1W分别是具有n-1 个钨原子和一个空位的超胞能量、具有n个钨原子的超胞能量、单个钨原子的能量. 计算结果如表5 所示.

表5 界面不同位置的钨空位形成能Table 5 Tungsten vacancy formation energy of different site on the interface

由表5 可知, 第一最近邻层的钨空位形成能明显小于第二最近邻和第三最近邻层的钨空位形成能, 这表明界面会吸收空位. 辐射损伤的根本原因是, 在高能粒子与目标原子之间的级联碰撞过程中, 产生了单个或聚集的空位以及自填隙缺陷[24]. 这些缺陷后续的扩散和聚集, 以及伴随的杂质迁移, 会导致材料出现蠕变加速、体积膨胀、合金元素偏析和脆化[25], 这些现象会严重限制辐射环境中材料和组件的寿命. 复合材料中的晶界和界面可以充当吸收缺陷的陷阱, 以减少基体中由辐照引起的缺陷[26-27]. 图7 展示了钨/石墨烷/钨第一壁材料对自填隙钨原子的影响, 该缺陷模型是通过去除一个钨原子形成空位, 以及增加一个自填隙钨原子而形成的(图7(a)为四面体间隙位置, 图7(c)为八面体间隙位置). 在弛豫前, 这些缺陷是致密的, 就像纯钨晶体中的空位和自填隙缺陷一样; 在弛豫后(见图7(b)和图7(d)), 自填隙钨原子与空位重新复合.

图7 界面处的自填隙钨原子和钨空位(粉色是自填隙钨原子, 黄色是空位)Fig.7 Self-interstitial tungsten atom and vacancy at the interface(the pink is self-interstitial tungsten atom, the yellow is vacancy)

由于空位和自填隙钨原子都被消除了, 因此可以将受石墨烷层影响的复合视为钨/石墨烷/钨第一壁材料中界面的“自修复”特征. 所以, 可通过促进空位和自填隙原子的复合来减少缺陷, 进而提高材料的抗辐照能力. 基于以上讨论, 本工作认为钨/石墨烷/钨第一壁材料中的界面不仅可以捕获氦原子和钨空位, 而且还是自填隙钨原子和空位的复合位点. 总之, 界面设计是减少钨体相中缺陷密度并增强材料抗辐射能力的有效策略.

2.3 力学性能

在宏观上, 材料的力学性质主要表现为材料的延展性、脆性和抵抗变形的能力, 同时表现在材料的强度和硬度等方面. 在微观上, 材料的力学性质是通过体积模量(B)、剪切模量(G)、杨氏模量(E)、泊松比(ν)、柯西压力值(C′)、各向异性因子(A)等物理量来体现. 对于立方晶体, 可以通过以下弹性常数的一组条件来表示机械稳定性[28],

钨/石墨烷/钨第一壁材料和纯钨金属的弹性常数均满足上述条件, 表明它们均符合弹性稳定性机制. 表6 列出了0 K 时纯钨金属和钨/石墨烷/钨第一壁材料的基本力学参数.

表6 0 K 下纯钨金属和钨/石墨烷/钨第一壁材料的基本力学参数Table 6 Basic mechanical parameters of pure tungsten metal and tungsten/graphane/tungsten as first wall material at 0 K

柯西压力可以描述材料的金属键和共价键行为, 柯西压力值越大, 金属键越牢固, 材料的延展性越好[29]. 由表6 可以看出, 与纯钨金属相比, 钨/石墨烷/钨第一壁材料的柯西压力(C′)显著增大, 这意味着钨/石墨烷/钨第一壁材料的延展性要好于纯钨金属. 各向异性因子(A)是指在不同方向上材料性能的差异. 材料失效前产生的微裂纹与各种因素有关, 例如弹性常数和热膨胀系数等物理量的各向异性容易在材料的晶界处产生应力, 从而导致晶界处形成裂纹. 若A= 1, 则材料表现为各向同性; 若A偏离1 越远, 则材料的各向异性程度越严重.钨/石墨烷/钨第一壁材料的各向异性因子(0.907)较纯钨金属(0.887)更接近1, 这说明钨/石墨烷/钨第一壁材料的各向异性程度较低. 作为托卡马克装置的第一壁材料, 各向异性程度越低,在受到高能粒子流轰击时, 出现裂纹的概率越低. 从第一性原理计算直接获得的弹性模量未考虑温度效应, 即在0 K 时的计算结果. 聚变反应器的工作温度通常在800～1 200 K的范围内,因此需要考虑温度对第一壁材料力学性能的影响. 托卡马克真空室的压力近似为0, 所以暂不考虑压力的影响. 将第一性原理和准简谐德拜模型结合, 可以计算出材料在不同温度下的力学模量. 图8～10 表示纯钨金属和钨/石墨烷/钨第一壁材料的体积模量(B)、杨氏模量(E)、剪切模量(G)随温度变化的情况. 可以看出, 钨/石墨烷/钨第一壁材料和纯钨金属的力学模量均随温度的升高而降低. 但在相同温度下, 钨/石墨烷/钨第一壁材料的3 个力学模量均低于纯钨金属, 并且钨/石墨烷/钨第一壁材料力学模量的下降速度要快于纯钨金属.

图8 纯钨金属和钨/石墨烷/钨第一壁材料的体积模量随温度的变化Fig.8 Bulk modules of pure tungsten metal and tungsten/graphane/tungsten as first wall material varies with temperature

图9 纯钨金属和钨/石墨烷/钨第一壁材料的杨氏模量随温度的变化Fig.9 Young’s modules of pure tungsten metal and tungsten/graphane/tungsten as first wall material varies with temperature

图10 纯钨金属和钨/石墨烷/钨第一壁材料的剪切模量随温度的变化Fig.10 Shear modules of pure tungsten metal and tungsten/graphane/tungsten as first wall material varies with temperature

2.4 热力学性质

2.4.1 定容热容

定容热容是指在加热过程中体积保持恒定, 物体不对外部工作, 并且外部提供的热量完全用于增加物体的内部能量, 反映了物体从周围环境吸收热量的能力. 定容热容直接反映系统内部能量的变化. 图11 表示钨/石墨烷/钨第一壁材料和纯钨金属的定容热容随温度变化的情况. 可以看出, 在低温区域(小于300 K), 两种材料的定容热容随温度升高而快速增大, 钨/石墨烷/钨第一壁材料的定容热容略大于纯钨金属; 在高温区(大于400 K), 两种材料的定容热容几乎不随温度的变化而变化, 这种关系符合Dulong-Petit 极限规律, 即高温下体系的定容热容等于3R(R=8.314 J·mol-1·K-1)[30]. 因此, 在高温区域, 石墨烷的加入对钨金属的定容热容影响不大.

图11 纯钨金属和钨/石墨烷/钨第一壁材料的定容热容随温度的变化Fig.11 Constant-volume heat capacity of pure tungsten metal and tungsten/graphane/tungsten as first wall material varies with temperature

2.4.2 吉布斯自由能和熵

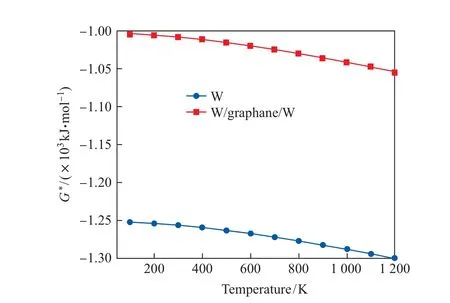
图12 纯钨金属和钨/石墨烷/钨第一壁材料的吉布斯自由能随温度的变化Fig.12 Gibbs free energy of pure tungsten metal and tungsten/graphane/tungsten as first wall material varies with temperature

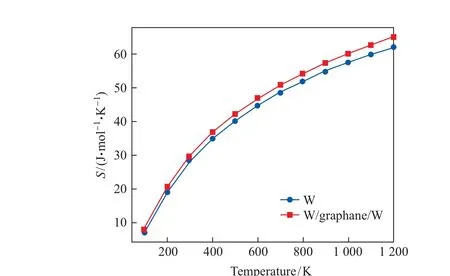
图13 纯钨金属和钨/石墨烷/钨第一壁材料的熵值随温度的变化Fig.13 Entropy of pure tungsten metal and tungsten/graphane/tungsten as first wall material varies with temperature

3 结 论

本工作首次设计将钨/石墨烷/钨体系作为托卡马克装置第一壁材料. 利用第一性原理研究钨/石墨烷/钨第一壁材料对钨空位形成能、填隙氦原子形成能、自填隙钨原子和弹性常数的影响, 并结合准简谐德拜模型计算了不同温度下的力学性能和热力学性质, 所得结论如下.

(1) 钨/石墨烷/钨第一壁材料中的界面可以作为吸收钨空位和填隙氦原子的陷阱, 降低钨空位与填隙氦原子的形成能, 从而减少钨空位与氦原子在钨体相中的聚集. 界面处的自填隙钨原子在弛豫后会与空位重新复合, 降低了第一壁材料中自填隙缺陷的密度. 钨/石墨烷/钨第一壁材料中的界面设计是减少钨体相中“氦气泡”和缺陷密度以及增强材料抗辐照能力的有效策略.

(2) 与纯钨金属相比, 钨/石墨烷/钨第一壁材料的柯西压力(C′)显著增大, 这说明材料的延展性得到提高. 并且钨/石墨烷/钨第一壁材料的各向异性因子值更接近1, 即各项异性程度在减弱, 这使得第一壁材料在遭受高能粒子流轰击时不容易产生裂纹.

(3) 与纯钨金属相比, 钨/石墨烷/钨第一壁材料在高温情况下的热力学稳定性有所降低.

致谢由衷感谢张兆春老师和郭海波老师对本工作的大力支持！感谢上海大学材料科学与工程学院Compmat 服务器集群提供的计算资源.