基于多目标的九轴五联动磨床整机分析与结构优化

梅益 薛茂远 甘盛霖 罗宁康 唐方艳 肖展开

摘要：現有的九轴五联动数控缓进给磨床运动环节多，在工作过程中可能出现刚度不足、床身等铸件变形及加工精度失准等问题.以磨床的最大变形量以及模态分析下的一阶固有频率作为主要优化目标，整身质量作为次要目标，利用ANSYS Workbench对磨床进行分析与优化，结合灵敏度分析对原有结构进行改进，得到各关键零部件新的设计方案，在磨床整机质量上升一定的程度上，磨床的最大静变形及一阶固有频率得到很大改进.再使用遗传算法（Genetic Algorithm）优化后的极限学习机网络模型（Extreme Learning Machine）联合遗传算法对该九轴五联动磨床改进结构的一些主要参数进行优化：首先，利用灰色关联分析将磨床的整机质量、最大静变形及一阶固有频率转成综合目标灰色关联度，其次，通过遗传算法优化后的极限学习机网络模型（Genetic Algorithm-Extreme Learning Machine）拟合改进磨床主要参数与综合目标灰色关联度之间的非线性耦合关系，最后，使用GA强大的寻优能力在训练好的GA-ELM网络模型中寻找最优工艺参数，优化后九轴五联动磨床的整机质量、最大静变形减小及一阶固有频率相对于改进方案得到优化.为后续相关工艺人员对该磨床的结构和参数优化提供一定理论支撑与参考价值.

关键词：九轴五联动数控缓进给磨床；灵敏度分析；结构优化；GA-ELM；GA-ELM-GA；参数优化

中图分类号：TH12文献标志码：A

Whole Machine Analysis and Structure Optimization of Nine-axis Five-linkage Grinder Based on Multi-objective

MEI Yi，XUE Maoyuan，GAN Shenglin，LUO Ningkang，TANG Fangyan，XIAO Zhankai

（School of Mechanical Engineering，Guizhou University，Guiyang 550025，China）

Abstract：The existing nine-axis five-linkage CNC slow-feed grinder has many motion links，which may cause many problems during the working process such as insufficient rigidity，deformation of castings like lathe bed and inaccurate machining accuracy. In this work，the maximum deformation of the grinder and the first-order natural frequency under the modal analysis are taken as the main optimization goal and the overall quality as the secondary goal. ANSYS Workbench is used to analyze and optimize the grinder，and the original structure is then improved by the sensitivity analysis，finally obtaining the new design scheme for each key part. When the quality of the whole grinder is improved to a certain extent，the maximum static deformation and first-order natural frequency of thegrinder is greatly improved. Besides，the extreme learning machine network model （Extreme Learning Machine）optimized by genetic algorithm is combined with genetic algorithm to optimize some main parameters of the improved structure of the nine-axis five-linkage grinder. Firstly，the whole machine mass，maximum static deformation and first-order natural frequency of grinding machine are transformed into comprehensive target grey correlation degree via grey correlation analysis. Then，the network model of the extreme learning machine （Genetic Algorithm-Extreme Learning Machine）optimized by the genetic algorithm is used to fit the nonlinear coupling relationship between the main parameters of the grinder and the gray correlation degree of the comprehensive target. Finally，GA's powerful optimization ability is used to find the optimal process parameters in the trained GA-ELM network model. After optimization，the overall quality of the nine-axis five-linkage grinding machine，the reduction of the maximum static deformation and the first-order natural frequency are optimized when compared with the improved scheme. This method provides a certain theoretical support and reference value for the subsequent technicians to optimize the structure and parameters of the grinder.

Key words：Nine-axis five-linkage CNC slow feed grinder；dynamic and static analysis；structure optimization；GA-ELM；GA-ELM-GA；parameter optimization

九轴五联动数控缓进给磨床样机在进行加工验证后，发现存在产品不良频率高、生产精度难以保证等问题，有必要针对磨床的整体结构及相应结构参数进行优化[1-2].结构优化方法有很多，比如Yun T等对一种飞机零件加工机床的头架结构进行拓扑优化，实现高刚度、低振动和轻量化的目标[3].Besharati等对龙门机床采用层次分析法、多目标遗传算法进行多目标选择与优化[4].但这些优化方法运用有限，目前人工神经网络具有很强非线性函数拟合能力，可以拟合变量与质量指标之间非线性耦合关系，再用优化算法对此网络模型寻优，能得到较优的工艺[5-6].本文利用Ansys Workbench軟件对磨床整机进行动静态特性分析与优化，同时结合灵敏度分析对原有结构进行改进，整机的一阶固有频率和最大静变形得到很大改善.再以整机一阶固有频率、最大静变形及整机质量为优化质量指标，使用灰色关联分析法将转成综合目标灰色关联度，再利用GA- ELM-GA对该磨床改进后的主要结构参数进行优化，优化后改进后的九轴五联动磨床的一阶固有频率、最大静变形及整机质量得以一定改进，验证了该多目标优化方法的有效性.结构改进及优化方法为后续制定新的磨床提供理论参考.

1磨床关键零部件参数化建模

1.1九轴五联动数控磨床样机运动分析

研究的磨床为某公司生产的MKH7150WJ九轴五联动数控缓进给磨床样机，如图1所示，初始定位精度0.003 mm.为了减少分析时间，忽略螺钉孔、圆角以及部分凸台等对分析结果影响不大的因素，将结构复杂却不需要进行细致分析的组件移除.采用等效力的方式体现在有限元分析环节，提升整个工作效率磨床的三维模型简化后如图2所示.磨床结构主要由床身、立柱、主轴箱、工作台和摇篮式工作台等零部件组成，床身与工作台、床身与立柱及立柱与主轴箱之间均通过滑块与滚珠丝杠体分别实现横向（X轴）、纵向（Y轴）及垂向（Z轴）三个方向上的运动，并通过摇篮式工作台实现两个旋转轴（A轴、C轴）方向的运动，如图3所示.

1.2主轴的参数化建模

主轴的设计是经过严格的验证得到的最佳方案，因此仅在有必要进行改进的情况下对主轴箱与立柱连接部分的高度H_D进行改进并参数化设置，便于满足实际加工条件，主轴部件结构如图4所示.

1.3立柱的参数化建模

立柱左右两侧内部布置有5块垂向筋板，横向布置有10块横筋板，如图5所示，采用这种格栅式筋板布置方式能有效地解决立柱参数的修改问题.

1.4床身的参数化建模

床身内部布置有7块筋板，其中前磨床床身有5 块纵筋板，后磨床床身有2块横筋板，如图6所示.采用布置筋板的方式，能有效地解决减少床身质量与提高床身稳定性之间互相矛盾的问题.

2磨床整机静力学及模态分析

2.1磨床整机应力分析

由图7可知，在模拟的实际加工工况下，磨床应力主要分布在中心加工位置，其最大应力7.4952 MPa 远低于材料的屈服应力250 MPa，后续优化不再讨论磨床整机等效应力，在实际加工过程中不会因应力集中而发生局部破坏.设计时可以进行轻量化处理.

2.2磨床整机刚度分析

由图8可知磨床整机的z方向变形量大于x、y方向的变形量，主要是由于径向磨削力引起的，也是影响整体变形量大的主要原因.有必要对整体结构改进，降低整机变形，使刚度分布相对更均匀.

2.3磨床整机模态分析

图9为磨床整机模态分析，磨床整机的前六阶固有频率为：63.724 Hz、83.128 Hz、94.907 Hz、119.36 Hz、124.94 Hz、126.04 Hz，其一阶振型为立柱主轴部分沿纵向摆动.其一阶固有频率大于主轴自转所能产生的最高频率50 Hz.因此在实际加工过程中并不会产生共振情况，整机具有良好的动态性能，但一阶固有频率高出主轴自转所能产生的最高频率不是太多，还是应该尽可能提升整机的一阶固有频率.

3基于灵敏度分析的磨床零部件改进

3.1主轴部件结构改进

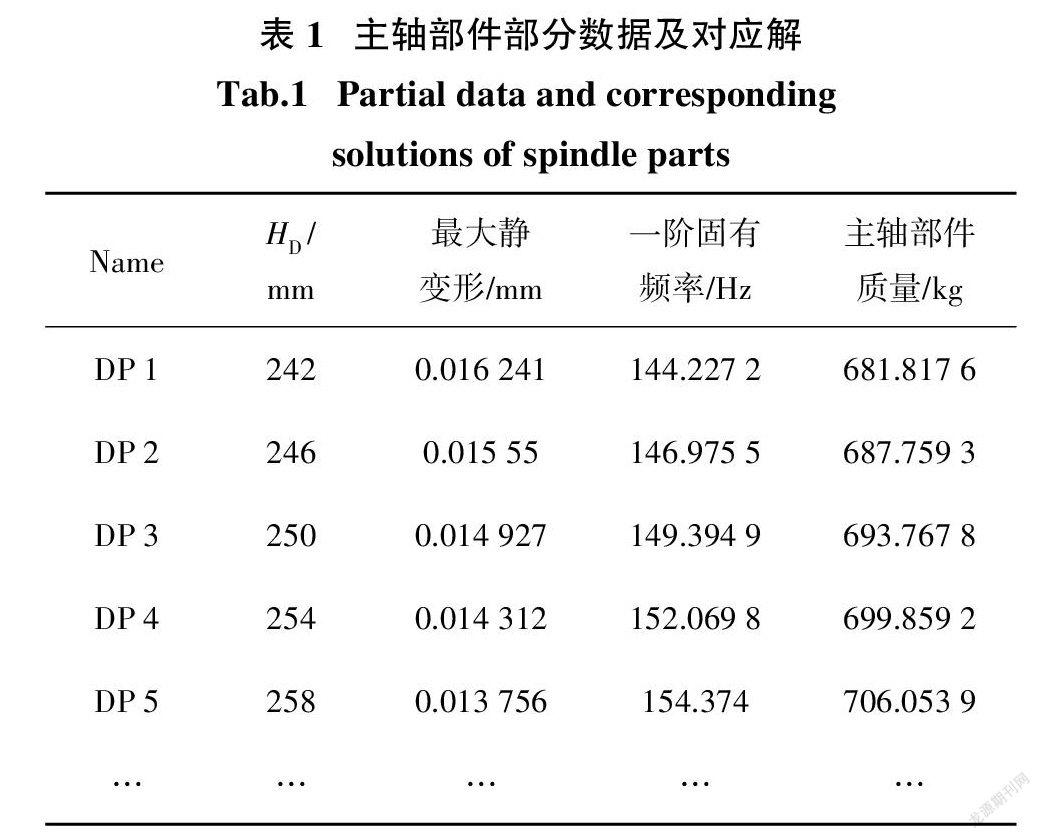
将主轴相关参数导入Direct Optimization模块进行寻优分析，生成的部分数据及对应解如表1所示.只有一个参数作为变量进行分析，其对各目标的灵敏度均为1，结合表1可以得出，当主轴箱高度增加，主轴部件与立柱间作用点距离变大，其作用力减小对主轴部件自身的固有频率及最大静变形都有不同程度改善.主轴箱内部结构复杂，简单地增加主轴箱高度H_D并不符合实际情况，因此采用局部改进的方法，通过设置加强筋的方式，增加主轴箱尾部高度，并将侧面也修改为筋板式，在增高尾部引起主轴箱质量增加的同时，也在侧面进行优化以减小一些主轴箱质量，改进后的主轴部件与原方案对比如图10 所示，将增加的主轴箱尾部上下高度参数H1、H2作为后续优化变量，如图11所示，目的在于提升主轴部件自身的固有频率，降低其最大静变形.

3.3立柱结构改进

将立柱相关参数导入Direct Optimization模块进行寻优分析，经计算生成的部分数据组及其对应解如表2所示，同时筛选出表3最佳多目标优化解集，根据多目标优化结果均值取整导入后续的结构分析[11-12]，其中各个变量对各目标函数的灵敏度如图12所示.

由图12可知，立柱整体质量会随着筋板厚度T₃及均布横向筋板数量M增加而增加，T₃对床身的最大静变形、整体质量及一阶固有频率有很大影响，选择T₃作为后续优化参数.立柱部分尺寸T₃、D₄、D₅与N₁对最大静变形存在一定影响，但结合表2的分析数据来看，其尺寸变化对于静变形的影响程度很小，且对于一阶固有频率来说，大部分尺寸与一阶固有频率大小几乎无关，由此可见，立柱内部筋板布置情况对于立柱部件结构的最大静变形及一阶固有频率影响很小，只是简单地对其进行增加或减小没有太大意义.为了减小变形，增大一阶固有频率，选择在立柱两侧中上位置增设加强筋，同时将加强筋厚度T4与T5作为后续优化目标，如图13所示.

3.3床身结构改进

基于Direct Optimization模块，根据床身相关参数设定100组解集进行寻优分析，其生成的部分数据组及对应解如表4所示，同时筛选出表5最佳多目标优化解集，根据多目标优化结果均值取整导入后续的结构分析，各个变量对目标函数的灵敏度如图14所示.

由图14可知，床身整体质量会随着筋板厚度增加而增加，床身部分尺寸T₁、T₂、d₂与d₃对最大静变形具有不同程度的影响，T₁、T₂、d₆与d₇对一阶固有频率具有显著影响，故应当对前床身与后床身的尺寸进行优化.T₁与T₂对床身的最大静变形、整体质量及一階固有频率有很大影响，选择T₁与T₂作为后续优化参数.除了对筋板尺寸优化外，还应对磨床后床身结构进行相应优化，结合实际需求，将筋板数量N作为后续优化目标，以此来提升磨床后床身整体结构强度，目的在于提升其一阶固有频率.如图15所示.

3.4改进后的整机模型

对改进后的整机模型进行动静态分析，如图16 所示.在对磨床关键零部件进行改进后，虽然磨床整体质量增加了11.68%，但其最大静变形减小28.83%，一阶固有频率提升31.28%，提升了磨床的工作精度与性能.

4基于灰色关联分析及GA-ELM-GA的磨

床整机多目标优化

磨床的结构复杂，若只是对组成磨床的各个关键零部件进行改进，无法有效地对磨床整体结构性能进行加强，因此应结合磨床关键零部件改进及分析情况，对磨床整机的相关工艺参数进行多目标优化，才能得出具有实际意义的优化方案[13-14].根据上文分析设置了表6参数及其取值范围.

4.1灰色关联分析

灰色关联分析可以对多目标问题进行综合评价，从而将多目标优化问题转换为单目标问题进行研究.主要步骤如下[15-17]：

1）确定比较系列Y_i（k）与参考系列式Y₀（k）.

2）本文的最大静变形与整机质量要求越小越好，使用望小公式归一化处理，如式（1）.一阶固有频率要求越大越好，使用望大公式归一化处理，如式（2）.

3）求灰色关联系数ξ_i（k），如式（3）.

式（3）中：Δ_i（k）为差序列，Δmax、Δmin为差序列的最大差与最小差，ρ为分辨系数，一般ρ=0.5.

4）计算灰色关联度γ，如式（4）.

式（4）中：γ为灰色关联度，w_j表示各质量指标的权重系数，本文j=3.

w_j可由变异系数法求得[18].变异系数法计算权重如式（5）.

通过ANSYS的Optimal Space-Filling Design对表6变量相应的范围生成500组的样本，通过上述步骤将整机质量、最大静变形及一阶固有频率三个质量指标转成综合目标灰色关联度.

4.2GA-ELM-GA优化模型

极限学习机（Extreme Learning Machine）有较强的非线性拟合能力，但由于ELM输入层与隐含层之间的权值矩阵w及隐含层神经元的阈值矩阵b随机产生，导致网络模型的预测拟合能力及预测稳定性不足.使用遗传算法寻找最优的w与b，得到预测能力及稳定性好的GA-ELM网络预测系统，此系统可以较好反映磨床工艺参数与综合目标灰色关联度之间非线性耦合关系，最终再通过遗传算法（GA）在训练好的GA-ELM网络预测模型中寻找最优磨床工艺参数[19-21].

GA-ELM-GA优化模型算法步骤如下：

1）输入500组样本数据，归一化处理，选择样本前400为训练样本，后100为测试样本，设置ELM网络模型的迭代次数100，种群大小50，隐含层神经元个数17.

2）利用遗传算法全局寻优能力寻找最佳的权值w与阈值b，在种群初始化阶段随机取权值w与阈值b，通过反复选择，交叉，变异等操作，获取最优的w与b.

3）将GA优化的权值和阈值传回ELM网络，得到GA优化的ELM网络模型，分析预测值与测试值之间的误差，检查系统预测精度.

4）通过遗传算法在训练好的GA-ELM网络预测模型中寻找最优工艺参数.确定遗传算法的优化目标为灰色关联度γ_min、优化变量及其约束范围.利用遗传算法强大的全局寻优能力寻找训练好的GA- ELM网络模型的最小翘曲变形及对应的工艺参数.将训练好的GA-ELM网络模型预测输出作为个体适应度值，根据适应度值大小筛选出灰色关联度γ最小个体，淘汰较差个体.通过选择、交叉、变异等操作寻找最优工艺参数.建立的遗传算法数学模型如式（6）[22].

式（6）中：f（T₁，T₂，N，T₃，T₄，T₅，H₁，H₂）为遗传算法的适应度函数.

4.3GA-ELM预测结果

图17为ELM与GA-ELM网络预测结果对比，可以看到直接使用ELM网络模型预测时，R²=0.801 23，均方误差为0.000 984 37，预测精度不够，而使用GA-ELM网络模型预测时，R²=0.965 41，预测精度得到很大提升，且相对误差大部分控制在5%以内，止匕GA-ELM网络模型作为预测模型可以较好反映磨床工艺参数与灰色关联度之间非线性耦合关系.可以用于后续GA寻优的预测模型.

4.4GA-ELM-GA尋优过程与结果

利用GA对GA-ELM进行全局极值寻优，图18为GA寻优适应度曲线，迭代约70代后，磨床的综合评价指标灰色关联度收敛于0.5926处，对应的尺寸T₁为11.35 mm，T₂为39.57 mm，N为4块，T₃为6 mm，T₄为35.37 mm，T₅为37.42 mm，H₁为85.43 mm，H₂为52.32mm.

4.5模拟验证

将GA-ELM-GA优化后8个磨床结构工艺参数导入ANSYS Workbench仿真平台进行验证，如图19所示.得到图20磨床整机优化后的最大静变形、整机质量及一阶固有频率，可以看到：GA-ELM-GA优化后九轴五联动磨床的整机质量与原始方案相比增11.68%，最大静变形减小29.68%，一阶固有频率提升了34.71%.

5模拟改进后新产品试制方案

结合结构优化及多目标优化结果，与实际相结合对磨床进行对比分析，得出用于新一代基础缓进给磨床试制的参考，并已初步完成了新一代样机试制，具体说明如下：

1）主轴箱在进行铸造后，用于带砂轮修整装置的磨床结构当中，如图21所示，其砂轮修整结构安装在主轴上方，其重量会平衡一部分径向磨削力带来的Z方向的变形，相当于增设尾部加强筋，还采用了文中的增加尾部滑块距离，牺牲一部分Z方向行程，来达到减小作用力的效果，相当于文中通过改进主轴箱尾部以减小最大静变形、增加磨床静刚度的改进方式.

2）通过分析得出，立柱结构的改进对于其最大静变形影响是很大的，因此，从提升磨床静刚度角度出发，有必要对立柱进行更为完善的改进.从文中有限元分析结果可知，现有的磨床立柱内部筋板的格栅式布局对立柱性能方面影响不大，文中仅是进行了轻量化处理，在进行综合考虑以后，实际样机还对内部筋板进行了重新设计，同时也参考文中对立柱侧面与立柱托板结合处的加强取得的显著效果，对该部分结构进行了加强处理，如图22所示.

3）图23为现场在整机安装前，仅安装磨床床身、立柱及主轴部件时照片，对磨床后床身进行了改进，从图中可以看到后床身部分筋板进行了增多，其主轴部件尾部也进行了相应的加高处理，且改进后的磨床选用了技术指标更为优异的丝杠、导轨等部件.图24为磨床定位精度测试图，定位精度由原来的0.003 mm变成0.0014，其性能得到明显提升.

6结论

1）针对目前九轴五联动数控缓进给磨床存在的问题，运用ANSYS Workbench建立了磨床关键零部件及整机的有限元模型，对磨床整机进行动静态特性分析，发现有必要对整机结构进行优化以减小最大静变形；通过模态分析结果得到，该磨床关键零部件及整机的一阶固有频率均大于主轴自转引起的振动频率，但整机的一阶固有频率不算太高，因此有必要在优化结构以减小最大静变形的同时，提升整机一阶固有频率.

2）根据ANSYS Workbench优化模块及灵敏度分析对磨床关键零部件进行了改进，改进后进行整机装配分析，最大静变形减小28.83%，一阶固有频率提升31.28%.

3）结合前面分析确定的磨床整机优化参数，通过灰色关联分析将三个目标转成综合目标灰色关联度，利用遗传算法优化后的极限学习机网络模型（GA-ELM）拟合磨床结构工艺参数与综合目标灰色关联度之间的非线性耦合关系，再通过遗传算法强大的寻优能力在训练好的GA-ELM网络模型中极值寻优.通过GA-ELM-GA优化后的最大静变形一阶固有频率及整机质量得到了优化.最后与工厂初试制产品进行对比分析，验证了进行一切工作的必要性.

参考文献

[1]施云高，杨爽，陈红，等.基于有限元法的轻量化支架力学分析[J].机械制造，2020，58（8）：10-13.

SHI Y G，YANG S，CHEN H，et al. Mechanical analysis of lightweight support based on finite element method [J]. Machinery，2020，58（8）：10-13.（In Chinese）

[2] BAERTSCH F，AMELI A，MAYER T. Finite-element modeling and optimization of 3D-printed auxetic reentrant structures withstiffness gradient under low-velocity impact [J]. Journal of Engineering Mechanics，2021，147（7）：（ASCE）EM. 1943-7889.0001923.

[3] YUN T，LEE S. Topology optimization design of machine tools head frame structures for the machining of aircraft parts [J]. Journal of Aerospace System Engineering，2018，12（4）：18—25.

[4]BESHARATI SR，DABBAGH V，AMINIH，et al. Multi-objective selection and structural optimization of the gantry in a gantry machine tool for improving static，dynamic，and weight and cost performance[J]. Concurrent Engineering，2016，24（1）：83-93.

[5]于长亮，张辉，王仁彻，等.机床整机动刚度薄弱环节辨识与优化方法研究[J].机械工程学报，2013，49（21）：11-17.

YU C L，ZHANG H，WANG R C，et al. Study on method for weak link identification of dynamic stiffness of a machine tool and optimization design[J]. Journal of Mechanical Engineering，2013，49（21）：11-17.（In Chinese）

[6]李艳萍，黄小平.基于BP-GA算法的环肋锥柱壳多目标优化设计[J].舰船科学技术，2021，43（3）：6-12.

LI Y P，HUANG X P. Multi-objective optimization design of ring- stiffened cone-cylinder shell based on BP-GA algorithm[J]. Ship Science and Technology，2021，43（3）：6-12.（In Chinese）

[7]孟鑫，张丹丹，杨晓楠.烟秆拔秆破碎机机架轻量化设计与动静态特性分析[J].农业技术与装备，2019（10）：88.

MENG X，ZHANG D D，YANG X N. Lightweight design and dynamic and static characteristics analysis of the straw stalk crusher frame [J]. Agricultural Technology & Equipment，2019 （10）：88. （In Chinese）

[8]毛继哲，邢佑兵，齐光辉，等.整体式多级离心压缩机大齿轮转子承载特性分析及关键制造工艺研究[J].现代制造工程，2021（3）：87-93.

MAO J Z，XING Y B，QI G H，et al. The loading characteristic analysis and key manufacturing process research of bull gear rotor in integrally multistage centrifugal compressors[J]. Modern Manufacturing Engineering，2021（3）：87-93.（In Chinese）

[9]馮帆.基于有限元方法的汽车减震系统建模与仿真分析[J].电子设计工程，2021，29（6）：16-19.

FENG F. Modeling and simulation analysis of automobile damping system based on finite element method[J]. Electronic Design Engineering，2021，29（6）：16-19.（In Chinese）

[10]马硕，姜兴宇，杨国哲，等.废旧机床主轴剩余寿命评估模型[J].机械工程学报，2021，57（4）：219-226.

MA S，JIANG X Y，YANG G Z，et al. Prediction and evaluation model for the residual life of wasted machine tool spindle[J]. Journal of Mechanical Engineering，2021，57（4）：219-226.（In Chinese）

[11]文孝霞，杜子学，申震，等.单轨车辆参数对轮胎磨损的影响及优化研究[J].机械设计与制造，2014（9）：214-217.

WEN X X，DU Z X，SHEN Z，et al. The monorail tire parameters affect on tire wear and optimization analysis on curve driving condition[J]. Machinery Design & Manufacture，2014（9）：214-217. （In Chinese）

[12]熊世磊，丁赛飞，王启慧，等.籽瓜破碎取籽分离机机架的有限元分析及优化[J].森林工程，2021，37（2）：86-94.

XIONG S L，DING S F，WANG Q H，et al. Finite element analysisand optimization of the frame of seed melon crushing separator[J]. Forest Engineering，2021，37（2）：86-94.（In Chinese）

[13]倪恒欣，阎春平，陈建霖，等.高速干切滚齿工艺参数的多目标优化与决策方法[J].中国机械工程，2021，32（7）：832-838.

NI H X，YAN C P，CHEN J L，et al. Multi-objective optimization and decision-making method of high speed dry gear hobbing processing parameters[J]. China Mechanical Engineering，2021，32 （7）：832-838.（In Chinese）

[14]杨泽青，吕硕颖，薄敬东，等.基于GRA-PCA的机床主轴系统热敏感点优化[J].机床与液压，2020，48（23）：93-98.

YANG Z Q，LV S Y，BO J D，et al. Thermal sensitive point optimization for machine tool spindle system based on GRA-PCA[J]. Machine Tool & Hydraulics，2020，48（23）：93-98.（In Chinese）

[15]王平，程贵海，邓春海，等.基于灰色关联分析法探析隧道中深孔楔形掏槽爆破[J].中国矿业，2020，29（11）：165-171.

WANG P，CHENG G H，DENG C H，et al. Exploration of wedge cutting blasting in tunnel based on grey relational analysis[J]. China Mining Magazine，2020，29（11）：165-171.（In Chinese）

[16]赵静，王选仓，丁龙亭，等.基于灰色关联度分析和支持向量机回归的沥青路面使用性能预测[J].重庆大学学报，2019，42（4）：72-81.

ZHAO J，WANG X C，DING L T，et al. Performance prediction of asphalt pavement based on grey relational analysis and support vector machine regression[J]. Journal of Chongqing University，2019，42（4）：72-81.（In Chinese）

[17]嚴嘉伦，林俊光，楼可炜，等.基于AHP-变异系数法的楼宇型综合能源系统评价体系[J].热力发电，2019，48（12）：25-30.

YAN JL，LINJG，LOU K W，et al. Evaluation system for building integrated energy system based on AHP-CV method[J]. Thermal Power Generation，2019，48（12）：25-30.（In Chinese）

[18] ZHENG G Z，HUA W H，QIU Z H，et al. Detecting water depth from remotely sensed imagery based on ELM and GA-ELM[J]. Journal of the Indian Society of Remote Sensing，2021，49（4）：947-957.

[19]孙全龙，梅益，杨幸雨.压铸模型腔曲面铳削表面粗糙度GA- ELM预测[J].机械设计与制造，2020（8）：188-191.

SUN Q L，MEI Y，YANG X Y. GA-ELM prediction of surface roughness of Die casting Die cavity surface milling[J]. Machinery Design & Manufacture，2020（8）：188-191.（In Chinese）

[20] ALHARBI A. A genetic-ELM neural network computational method for diagnosis of the Parkinson disease gait dataset[J]. International Journal of Computer Mathematics，2020，97（5）：1087- 1099.

[21]刘强，陈洪荣，梅端，等.基于正交试验与BPNN-GA的航标灯外壳注塑工艺参数优化[J].塑性工程学报，2020，27（7）：123-129.

LIU Q，CHEN H R，MEI D，et al. Process parameters optimization of injection molding of beacon light cover based on orthogonal test and BPNN-GA[J]. Journal of Plasticity Engineering，2020，27 （7）：123-129. （In Chinese）

[22] QI J T，ZHAO W W，KAN Z，et al. Parameter optimization of double-blade normal milk processing and mixing performance based on RSM and BP-GA[J]. Food Science & Nutrition，2019，7 （11）：3501-3512.