反思题目通法 突出变换引领
——2021年南通市中考试题第25题赏析*
张 俊 (山东省淄博市周村区城北中学 255300)
时翠萍 (山东省淄博市周村区第二中学 255300)
笔者近来研究2021年南通市中考试题第25题时,发现该题以最基本的图形变换“轴对称”为背景,渐次生长,思路开阔,是一道值得回味的题目,特撰文与大家交流.
1 原题呈现
如图1,正方形ABCD中,点E在边AD上(不与端点A,D重合),点A关于直线BE的对称点为点F,连结CF,设∠ABE=α.

图1
(1)求∠BCF的大小(用含α的式子表示);
(2)过点C作CG⊥AF,垂足为G,连结DG.判断DG与CF的位置关系,并说明理由;
(3)将△ABE绕点B顺时针旋转90°得到△CBH,点E的对应点为点H,连结BF,HF.当△BFH为等腰三角形时,求sinα的值.
2 思路突破
2.1 基于对称变换,构造对称图形


图2
2.2 导角突破难点,多维角度探寻
如图2,对于第(2)问,学生可以直观判断出DG与CF的位置关系,但如果要说明理由,对大多数学生来说有一定的难度,此时题目已经进入宽进难出的环节.那么突破的方向在哪里呢?在此问中,有一个“知识坎”很多学生未能逾越,导致问题探究无法进行到下一步.在这里我们有必要细细品味一下:在图2中,很多学生凭直观猜测出了△CGF是等腰直角三角形,但一直无法说明∠AFC=135°(这里考查了学生利用带有字母的角的导角能力).如图3,基于前面的分析我们可以得到∠AFB=90°-α,∠BFC=∠BCF=45°+α,所以可得∠AFC=∠AFB+∠BFC=90°-α+45°+α=135°.从而可以看到,尽管点F的位置是变化的,但∠AFC始终是一个定角.那该问题的本质在哪里?因为BA=BF=BC,所以点F在以点B为圆心、BA为半径的圆上运动,根据定弦对定角,可知∠AFC始终为135°.解决了这一问题,就为后面的探究做好了铺垫.

图3


图4 图5

思路3 如图6,从点共圆的角度,连结对角线AC.因为∠ADC=∠AGC=90°,所以点A,D,G,C在以AC中点O为圆心、OA为半径的圆上.在同圆中,可得∠DGA=∠ACD=45°,即∠CFG=∠DGA=45°,故DG∥CF.
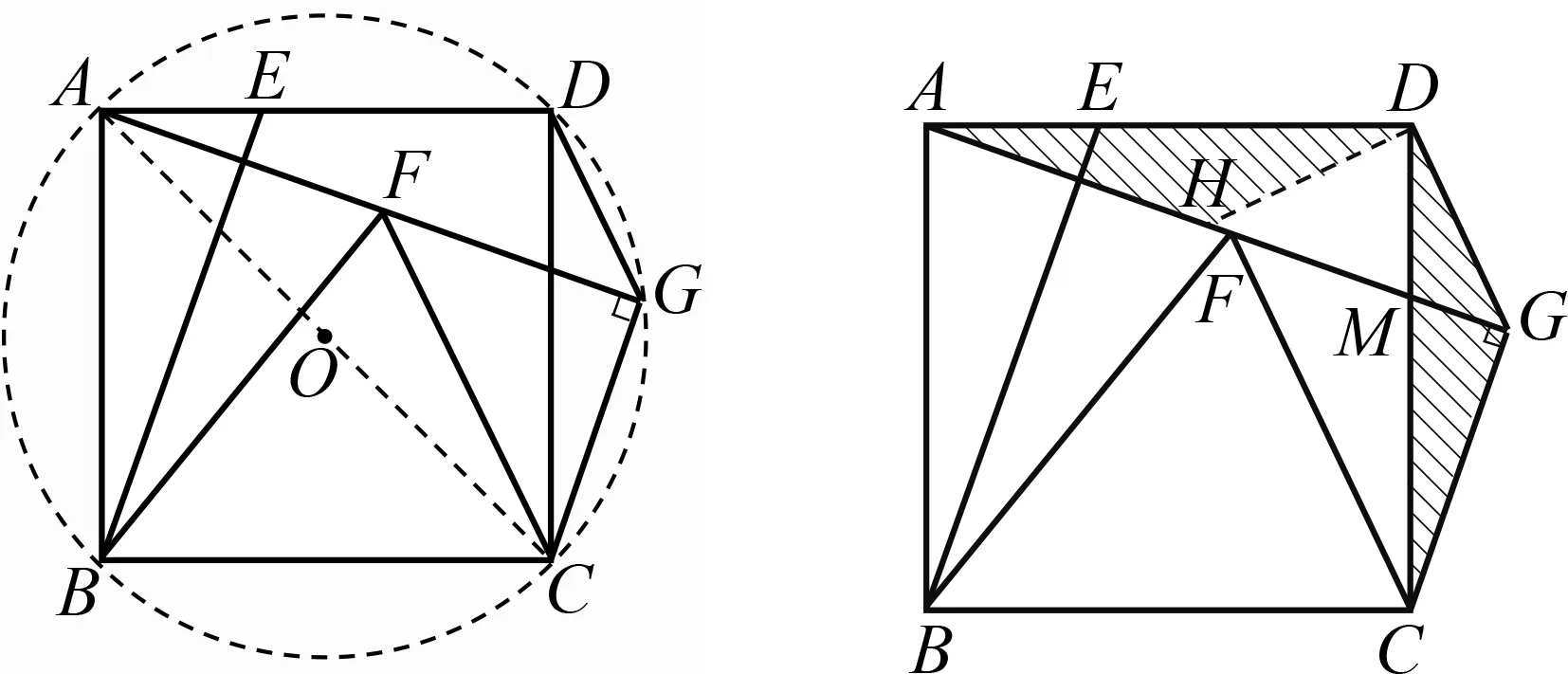
图6 图7
思路4 如图7,从构造全等三角形角度来思考,在AG上截取AH=CG.因为∠AMD=∠CMG,∠ADM=∠CGM=90°,所以∠DAH=∠DCG.又有AD=CD,所以△DAH≌△DCG,可得∠ADH=∠CDG,HD=GD.因为∠ADH+∠HDM=90°,所以∠HDG=90°,此时△HDG是等腰直角三角形,故∠DGH=45°,即∠CFG=∠DGH=45°,从而DG∥CF.
2.3 始于分类讨论,终于转化分析
第(3)问以旋转为背景,重点考查了分类讨论的思想.本题的难度还是在分类后的验证上,对学生的说理能力要求较高.如图8,对于△BFH为等腰三角形,我们考虑:①当BF=BH时,由于△BAE≌△BCH,所以BH=BE,又因为BA=BF,这时出现了BE=BA,在Rt△BAE中是不可能的,显然这种情况不存在.②当BF=HF时,∠FBH=∠FHB=90°-α,可得∠BFH=2α,由于∠ABF=2α,所以此时AB∥FH,即点F与点C要重合,则需要点E运动到点D,与题意不相符,因此这种情况也不存在.相比第①种情况的验证,第②种情况的验证要求学生进行适当的推理说明,综合性较强.结合上述分析,只有一种可能是BH=FH,此时解决问题的方向又在哪里?

图8


3 深入思考


图9
第(2)问的思路2是基于“8”字相似的成对存在性,如图5,若△ADM∽△CGM,则必有△DMG∽△AMC,本身构成这样相似的点D,G,A,C与思路3的四点共圆是一致的.
第(3)问的第二种思路如同神来之笔,连结EC,构造的其实是一对具有对称性的全等三角形,△BFH≌△BCE,并且关于直线BN成轴对称(图10).基于图形的对称,联想到全等,这其实就是一种发现对称美的过程.
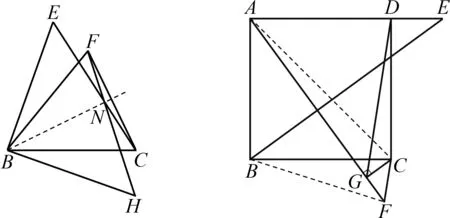
图10 图11
基于本题图形的变化,我们考虑再进行一下变式的生长:原题点E在线段AD上运动,我们让点E在射线AD上运动,其他条件保持不变,此时仍然可以得到DG∥CF(图11).


图12
当然本题还有其他方法,这里不再赘述.现在我们改变对称点,继续思考一下.如图12,作点C关于BE的对称点F,连结BF,作AG⊥FC,垂足为G,连结DG,求证:DG∥AF.
这里通过推导角度仍然可得△AGF为等腰直角三角形,连结AC,此时△AGF与△ADC是相似的等腰三角形,由旋转相似的成对性,还可以得出△DAG∽△CAF,进而问题可以突破.
我们让该问题在此基础上继续生长.如图13,正方形ABCD中,点E在边AD上(不与端点A,D重合),点C关于直线BE的对称点为点F,连结CF,BF,同时连结FA,BE并分别延长交于点G,连结DG,设∠ABE=α.
(1)求∠BGF的大小;
(2)猜想DG与AF之间的数量关系,并说明理由.


图13 图14
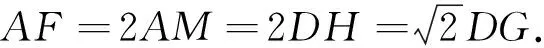
4 教学反思
4.1 重视基本图形渗透,强化识图能力
基本图形是复杂图形组成的基本元素,主要包括教材上的基本事实和定理及其推论,以及在平时教学中获得的一些典型图形.学生之所以解题时没有思路,关键就是没有从复杂的图形里把基本图形抽取出来.正如2021南通市中考第25题,其中蕴含的基本图形非常多,例如旋转相似的成对存在性,以及“8”字型相似的成对性、四点共圆等,如果学生没有较强的识图能力,是很难突破问题的.因此,教师在平时的教学中要为学生及时总结和提炼一些基本图形,对其应用条件和基本结论要熟悉.这里要特别注意一点,千万不能让学生死记,而要引导学生从已知条件中挖掘关键条件,找到问题的核心,回归到书本上最基本的定义和定理,这样才能真正实现基本图形与数学概念的有效结合.只有这样潜移默化地不断渗透,学生才能逐步形成基本图形分析观念,在面对几何问题时,主动寻找或构造头脑中的基本图形,运用其来解决问题.
4.2 突出几何变换引领,积累构图经验
初中的图形变换分为两种,一种是全等变换,主要包含平移、旋转、轴对称,另一种是相似变换,指的是相似与位似,新课标也特别提倡让图形运动起来,让学生在运动中发现不变.然而实际情况是,学生仍然习惯于静态地去思考问题,这导致他们不能深入问题的本质.比如南通这道中考题,以正方形作为背景,正方形本身就是轴对称和中心对称图形,从点A与点F关于直线BE对称入手,引导学生构造对称图形,然后通过构造旋转相似这一变换作为解决问题的主线,继续生长,第(3)问基于图形的旋转分类思考,最终呈现了一对对称性的全等三角形.可以说本题始于轴对称,发展于旋转,最终止于轴对称,整个解答的过程都突出了几何变换的统领.因此,在平时的教学中,教师要多引导学生从几何变换的视角来分析几何图形,通过这种运动的观点构造出准确的图形,这样学生就会站在更高的高度来认识几何图形.长此以往,可以让学生养成从几何变换的视角来审视几何问题的习惯,促进学生数学素养和解题能力的提升.

