方程组有解问题转化为方程有解问题的思考*
2022-11-14 16:30俞杏明
中学数学月刊 2022年3期
俞杏明
(江苏省兴化中学 225700)
数学问题解决过程中,经常需要把方程组有解问题,转化为方程有解问题,这必须考虑转化是否等价.
1 解答质疑引发思考


2 溯源而上挖掘隐含
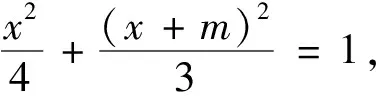
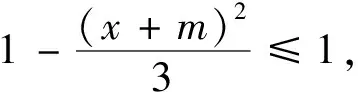
所以方程7x2+8mx+4(m2-3)=0若有解,则解一定在[-2,2]内.
3 提炼升华生成结论



同理有:

例2若2x2-2xy+y2=1,求x+2y的最小值与最大值.

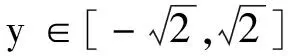


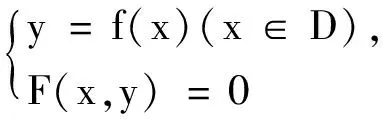
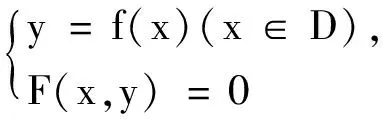
类似地,

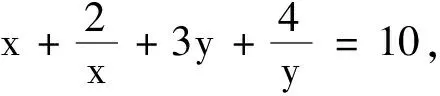
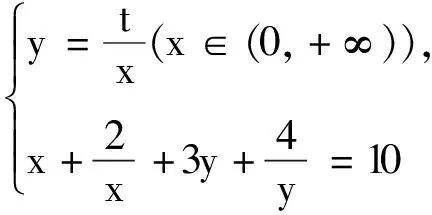

4 隐含对应一一兼顾
方程组有解问题转化为方程有解问题时,有时会出现意想不到的错误.
例4若曲线C1:y2=2x与曲线C2:(x-m)2+y2=2有交点,求m的取值范围.
这个答案显然是错误的,当m取较小负数时,两曲线处于相离状态,没有交点.那么,错误的根源是什么?如何避免这样的错误?下面先从简单事例入手进行探讨.




对刚才的例子进行一般化,有如下结论:

同理有:

更一般地,有以下结论:


下面我们重新求解例4.

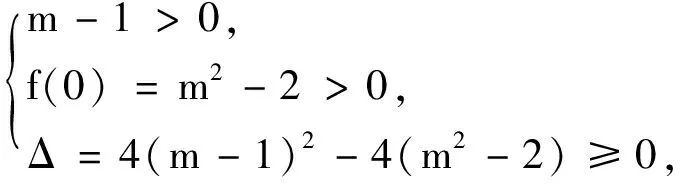
把例4改编为下面两道例题,体现推导出的结论的效力.
例5若曲线C1:y2=2x与曲线C2:(x-m)2+y2=2有四个交点,求m的取值范围.
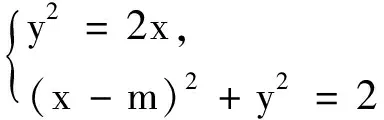
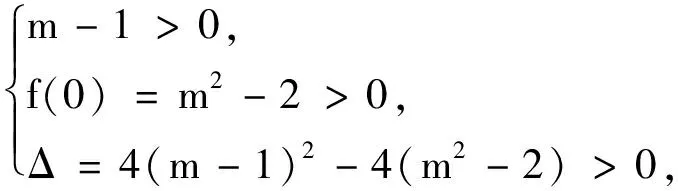
例6已知曲线C1:y2+4y=2x与曲线C2:(x-m)2+y2+4y=2有且仅有两个公共点,求m的取值范围.
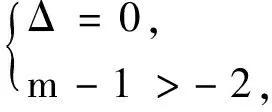
5 一点说明
代入消元法是处理方程组最基本、最常用的办法.有些方程组尽管需要特殊技巧整理,但最终仍回归到代入消元法轨道上.至于更多元(二元以上)的方程组,可以在文中理念下等价转化为二元方程组,进而用文中结论求解.
猜你喜欢
中学生数理化·七年级数学人教版(2022年5期)2022-06-05
河北理科教学研究(2020年3期)2021-01-04
语数外学习·初中版(2020年5期)2020-09-10
疯狂英语·新悦读(2019年10期)2019-12-13
重型机械(2019年3期)2019-08-27
数学物理学报(2019年3期)2019-07-23
发明与创新(2019年2期)2019-01-12
新教育(2018年8期)2018-08-29
发明与创新·中学生(2016年3期)2016-03-29
中学生数理化(高中版.高二数学)(2016年4期)2016-03-01

